例谈综合问题解题方法之变式生成

湖北省武汉市华中科技大学同济附中(430030) 高洪涛 王凯旋

一、问题提出

在教学中,有很多学生反映,上课能听懂老师的讲解,但是自己再遇到类似的题目还是不会解.如果是一道新类型的问题,更不知如何下手.当然,我们可以从老师和学生的角度进行分析.很多老师的论文已经多角度的分析了这个问题,在此,不做太多的重述.本文计划从另一个角度即解题方法的习得展开探讨.“解题是数学的心脏”,中学数学活动,离不开解题这个重要环节.而解题,必然涉及到解题方法,解题方法从何而来?大概有这样几种途径:来自于课堂从老师那里获得的解题方法;来自于所订阅的期刊杂志或者教辅资料;来自于和老师、同学交流以后所感悟出来的;还有一种,往往被我们所忽视,就是来自于我们所要解决的问题.在一些综合问题中,往往有多个小问题,形成问题串的方式呈现出来,前面的小问题或者为后面的小问题提供了条件,结论(另文书写),或者为后面的小问题提供了方法.但是,我们的学生在解题的过程中,割裂了各个问题之间的联系,总是想另起炉灶,苦思冥想,而忽视了近在眼前的方法宝藏.下面,通过典型案例,来说明如何在解答综合问题时得到解题方法的变式生成.

在我们需要解答的综合问题中,很多时候,就是一个变式的问题串.后面的问题中的图形结构和第一个问题的图形结构相比,或者进行了变式构造,或者只保留了部分结构.那么,在解答后面问题的时候,我们需要补全图形,采用相似的方法,完成综合问题的解答.这种解题方法的获得,来自于我们需要解决的问题.

二、案例分析

案例 1已知:CA=CB,CD=CE,∠ACB=∠DCE=90°,M,N,F分别是AE,BD,DE的中点,连接FM,FN.

(1)如图1,当A,D,C在一条直线上时,求证:①FM=FN;②FM⊥FN;

图1

图2

分析问题已知条件中已经出现多个中点和中位线,可以考虑利用中位线定理完成解答.

解①因为CA=CB,CD=CE,所以AD=BE.因为M,N,F分别是AE,BD,DE的中点,所以且FM//AD,FN//BE,所以FM=FN.

②如图2,延长FM交BC于G,由①得:FM//AD,FN//BE,因为 ∠ACB=90°,所以 ∠MGB=∠ACB=90°,所以FM⊥BC,所以FM⊥FN.

(2)如图3,当B,D,C在一条直线上时,上述①②是否成立?

图3

图4

分析第二问实质是第一问的简单变式,根据变式生成的方法生成模式,保持第一问的相似结构和方法.

解①如图4,连接AD,BE,延长AD交BE于G点,因为CA=CB,CD=CE,∠ACB= ∠DCE=90°所以△ACD△BCE,所以AD=BE,∠CAD=∠CBE.因为M,N,F分别是AE,BD,DE的中点,所以且FM//AD,FN//BE,所以FM=FN.

②由①得∠CAD=∠CBE,又因为∠ADC=∠BDG,所以∠BDG= ∠ACB=90°,所以AD⊥BE,又因为FM//AD,FN//BE,所以FM⊥FN.

案例2已知△ABC,以为AC边在△ABC外作等腰△ACD,其中AC=AD.

(1) 如图 5,若AB=AE,∠DAC= ∠EAB=60°,求∠BFC的度数.

图5

解因为∠DAC=∠EAB=60°,所以 ∠CAE= ∠BAD.因为AC=AD,AB=AE,所以△ABD,所以 ∠AEC= ∠ABD,所以∠BFE= ∠EAB=60°,所以 ∠BFC=180°−∠BFE=60°.

(2) 如图 6,若 ∠ABC=30°,∠ACD=60°,BC=4,BD=6,求AB的长.

图6

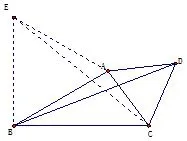
图7

分析从第一问到第二问,好似从完整到残缺,第一问的两边都有等边三角形,而第二问只有一边有等边三角形,根据变式生成方法的模式,保持第一问的相似结构和方法,我们在三角形的另一边补充一个等边三角形试一试.

解如图7,以AB为边,在△ABC外作等边三角形△ABE,连接CE,则 ∠ABE= ∠BAE=60°,BE=AB=AE,所以∠DAB= ∠EAC,又因为AC=AD,所以△ABD△ACE,所以BD=CE=6.因为BC=4,因为 ∠ABC=30°,所以 ∠EBC=90°.在 Rt△BCE中,所以

(3)如图 8,AB=2,BC=5,∠ABC= ∠ACD=∠ADC=45°,则BD的长.

图8

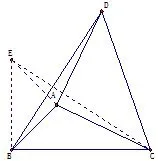
图9

分析从第一问,第二问到第三问,从完整到残缺,从等边三角形到等腰直角三角形.第一问的两边都有等边三角形,第二问也需要两边有等边三角形,但是,第三问和第一问相比也是残缺的,和第二问相比三角形从等边三角形,变为等腰直角三角形.根据变式生程方法的模式,保持第一问的相似结构和方法我们在三角形的另一边补充一个等腰直角三角形试一试.

解如图9,以AB为边,在△ABC外作等腰直角三角形△ABE,使,AB=AE,∠EAB=90°,连接CE.因为 ∠ACD= ∠ADC=45°,所以AD=AC,∠CAD=90°. 因为AB=AE,∠EAB=90°,所以 ∠CAE=∠BAD,所以△ABD△ACE,所以BD=CE.因为 ∠ABC= ∠ABE=45°所以 ∠EBC=90°. 因为AB=2,BC=5,所以因为在 Rt△BCE中,所以

案例3(1)如图10,若点M,N分别在正方形ABCD的边BC,DC的延长线上,且 ∠MAN=45°,请探求S△AMN,S△ABM,S△ADN之间的等量关系,并证明;

(2)如图,在△ABC中,∠MAN=45°,且AD⊥BC于D,若BD=3,CD=10,求S△ABC.

图10

图11

解如图11,在DC上截取DQ=BM,连接AQ,因为四边形ABCD正方形所以AB=AD,∠ABM=∠ADQ,所以△ABM△ADQ,所以S△ABM=S△ADQ,AM=AQ.设∠BAM= ∠DAQ=x,∠BAN=y,则x+y=45°,所以∠QAN=90°−(∠BAN+∠DAQ)=90°−(x+y)=45°,所以 ∠MAN= ∠QAN. 又因为AN=AN,所以△AMN△AQN,所以S△ANM=S△ANQ,所以S△AMN+S△ABM=S△ADN.

图12

图13

分析从第一问到第二问,从完整到残缺,第一问存在一个正方形,而第二问只有一个三角形,根据变式生成方法的模式,保持第一问的相似结构和方法,以AD为边,构造一个正方形试一试.