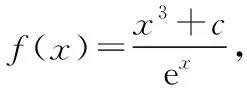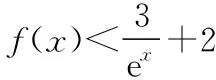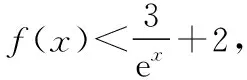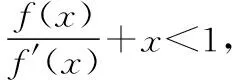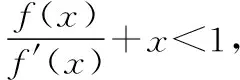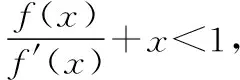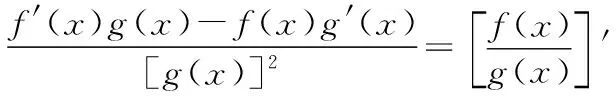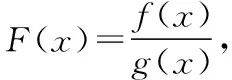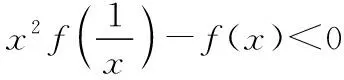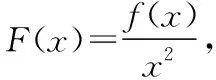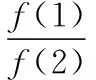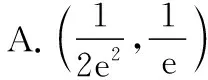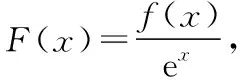联想导数运算法则 巧设可导函数解题
——抽象函数背景下导数运算法则的逆用、变用综述
四川 蔡勇全
一、巧设“y=f(x)±g(x)”型可导函数
当题设条件中存在或通过变形出现特征式“f′(x)±g′(x)”时,不妨联想、逆用“f′(x)±g′(x)=[f(x)±g(x)]′”,构造可导函数y=f(x)±g(x),然后利用该函数的性质巧妙地解决问题.
例1设奇函数f(x)是R上的可导函数,当x>0时,有f′(x)+cosx<0,则当x≤0时,有
( )
A.f(x)+sinx≥f(0)
B.f(x)+sinx≤f(0)
C.f(x)-sinx≥f(0)
D.f(x)-sinx≤f(0)
提示观察条件中“f′(x)+cosx”与选项中的式子“f(x)+sinx”,发现二者之间是导函数与原函数之间的关系,于是不妨令F(x)=f(x)+sinx,因为当x>0时,f′(x)+cosx<0,即F′(x)<0,所以F(x)在(0,+∞)上单调递减,又F(-x)=f(-x)+sin(-x)=-[f(x)+sinx]=-F(x),所以F(x)是R上的奇函数,且F(x)在(-∞,0)上单调递减,F(0)=0,并且当x≤0时有F(x)≥F(0),即f(x)+sinx≥f(0)+sin0=f(0),故选A.
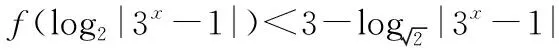
( )
A.(-∞,0)∪(0,1)
B.(0,+∞)
C.(-1,0)∪(0,3)
D.(-∞,1)

变式2设函数f(x),g(x)在区间[a,b]上可导,且f′(x)>g′(x),则当a ( ) A.f(x)>g(x) B.f(x) C.f(x)+g(a) D.f(x)+g(b) 提示由条件式f′(x)>g′(x)得f′(x)-g′(x)>0,可构造F(x)=f(x)-g(x),由于函数f(x),g(x)在区间[a,b]上可导,故函数F(x)在区间[a,b]上也可导.由题意可知,F′(x)=f′(x)-g′(x)>0在区间[a,b]上恒成立,故函数F(x)=f(x)-g(x)在区间[a,b]上单调递增,所以对于任意x∈(a,b)恒有F(x) 变式3设定义在R上的函数f(x)满足f(0)=-1,其导函数f′(x)满足f′(x)>k>1,则下列结论一定错误的是 ( ) 变式4设定义在R上的函数f(x)满足f(1)=2,f′(x)<1,则不等式f(x2)>x2+1的解集为______ . 提示由条件式f′(x)<1得f′(x)-1<0,待解不等式f(x2)>x2+1可化为f(x2)-x2-1>0,可以构造F(x)=f(x)-x-1,由于F′(x)=f′(x)-1<0,所以F(x)在R上单调递减.又因为F(x2)=f(x2)-x2-1>0=2-12-1=f(12)-12-1=F(12),所以x2<12,解得-1 评注以上案例中,例1及变式2属于直接给出特征式“f′(x)±g′(x)”的类型,而对于变式1,3,4,则属于间接给出特征式“f′(x)±g′(x)”的类型,且主要以“f′(x)±k(k为常数)”为特征式,需要构造出可导函数f(x)±kx解决问题.事实上,无论是题目中直接抑或间接出现特征式“f′(x)±g′(x)”,其解题本质概括起来就是“构造和(差)函数、强化恒成立”. 当题设条件中存在或通过变形出现特征式“f′(x)g(x)+f(x)g′(x)”时,可联想、逆用“f′(x)g(x)+f(x)g′(x)=[f(x)g(x)]′”,构造可导函数y=f(x)g(x),然后利用该函数的性质巧妙地解决问题. 例2设函数f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(3)=0,则不等式f(x)g(x)>0的解集是 ( ) A.(-3,0)∪(3,+∞) B.(-3,0)∪(0,3) C.(-∞,-3)∪(3,+∞) D.(-∞,-3)∪(0,3) 提示构造条件中“f′(x)g(x)+f(x)g′(x)”与待解不等式中“f(x)g(x)”两个代数式之间的关系,可构造函数F(x)=f(x)g(x),由题意可知,当x<0时,F′(x)>0,所以F(x)在(-∞,0)上单调递增.又因f(x),g(x)分别是定义在R上的奇函数和偶函数,所以F(x)是定义在R上的奇函数,从而F(x)在(0,+∞)上单调递增,而F(3)=f(3)g(3)=0,所以F(-3)=-F(3),结合图象可知不等式f(x)g(x)>0⟺F(x)>0的解集为(-3,0)∪(3,+∞),故选A. 变式1设定义在R上的函数f(x)满足f′(x)+f(x)=3x2e-x,且f(0)=0,则下列结论正确的是 ( ) A.f(x)在R上单调递减 B.f(x)在R上单调递增 C.f(x)在R上有最大值 D.f(x)在R上有最小值 ( ) A.对于任意x∈R,f(x)<0 B.对于任意x∈R,f(x)>0 C.当且仅当x∈(-∞,1)时,f(x)<0 D.当且仅当x∈(1,+∞)时,f(x)>0 变式4设y=f(x)是(0,+∞)上的可导函数,f(1)=2,(x-1)[2f(x)+xf′(x)]>0(x≠1)恒成立.若曲线f(x)在点(1,2)处的切线为y=g(x),且g(a)=2 018,则a等于 ( ) A.-501 B.-502 C.-503 D.-504 提示由“2f(x)+xf′(x)”联想到“2xf(x)+x2f′(x)”,可构造F(x)=x2f(x)(x>0).由(x-1)[2f(x)+xf′(x)]>0(x≠1)可知,当x>1时,2f(x)+xf′(x)>0,则F′(x)=2xf(x)+x2f′(x)>0,故F(x)在(1,+∞)上单调递增;当0 评注总体上看,上述例2及其几个变式都是在构造“f(x)g(x)”型可导函数解决问题,区别在于:例2及其变式1是无需变形的直接构造,且变式1在求出c的值之前,不仅逆用了导数运算法则,而且从导函数角度写出了原函数的解析式,而变式2,3,4则需要先对条件或所求结论中的特征式作出适当的变形后再构造出相应的“f(x)g(x)”型可导函数.值得一提的是,解答变式2时构造可导函数的策略实际上是受了变式1的解法的启发.另外,我们需要归纳掌握一些常用的构造方法:①当题设或所求结论中具有特征式“f′(x)+f(x)”时,可构造F(x)=exf(x);②当题设或所求结论中具有特征式“f′(x)+f(x)+k(k为常数)”时,可构造F(x)=exf(x)+kex;③当题设或所求结论中具有特征式“xf′(x)+nf(x)(n为常数)”时,可构造F(x)=xnf(x);④当题设或所求结论中具有特征式“f′(x)+nf(x)(n为常数)”,可构造F(x)=enxf(x).需要指出的是,方法①实际上是方法④的特殊情形. 例3已知定义在R上函数f(x),g(x)满足:对任意x∈R,都有f(x)>0,g(x)>0,且f′(x)g(x)-f(x)g′(x)<0.若a,b∈R+且a≠b,则有 ( ) 变式2设函数f(x)是R上的奇函数,f(-1)=0.当x>0时,(x2+1)f′(x)-2xf(x)<0,则不等式f(x)>0的解集为______ . 变式3设f′(x)是函数f(x)(x∈R)的导函数,且满足xf′(x)-2f(x)>0,若在△ABC中,角C为钝角,则 ( ) A.f(sinA)·sin2B>f(sinB)·sin2A B.f(sinA)·sin2B C.f(cosA)·sin2B>f(sinB)·cos2A D.f(cosA)·sin2B ( ) C.(e,2e) D.(e,e3)
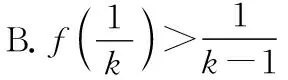
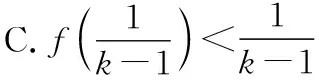
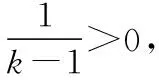
二、巧设“f(x)g(x)”型可导函数