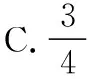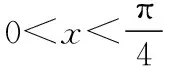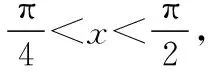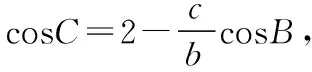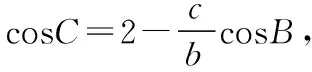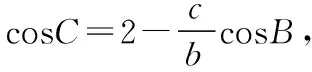原创研发活动的四点思考
湖北 廖庆伟
2017年6月《教学考试》高中数学第一期原创研发活动正式开始,两个半月的时间,通过《教学考试》的编辑、命题组教师、审稿组教师的细致交流、探讨,顺利完成了试卷研发任务.仔细回想活动的各个环节,制定《双向细目表》、命题、磨题、审题、修改调整、定稿.值得思考的问题有四点.
一、重视《双向细目表》的导向功能
一份高质量的试卷体现内容很多,通过双向细目表来规划、约束,能更好地保证试题的质量.依据《新课程标准》和《考试说明》命题不会超纲,不会出繁、难、偏、旧的题目,对照《细目表》逐个知识点进行落实是命题人的重要任务.

数学命题双向细目表初稿与终稿对比
二、原创改编耐人寻味、闪耀数学思想
高考数学的新考纲在能力要求方面,增加了基础性、综合性、应用性、创新性的要求,增加了数学文化的要求,同时对能力要求进行了细化说明,使能力要求更加明确具体.
命制一套试卷在稳定中要有一定的创新,重视考查学生的核心数学素养,不仅要兼顾知识点、思想方法与能力的考查,也要关注数学的应用意识与创新意识.一套好的试卷,应整体性的反应考试的目的和理念.此外,原创题至少要包括“自编、创新”,“原”即作者首创,不抄袭他人;“创”即创新,新颖独到.原创改编耐人寻味、闪耀数学思想.
考查数形结合思想的题目:
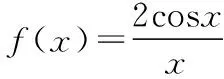
( )
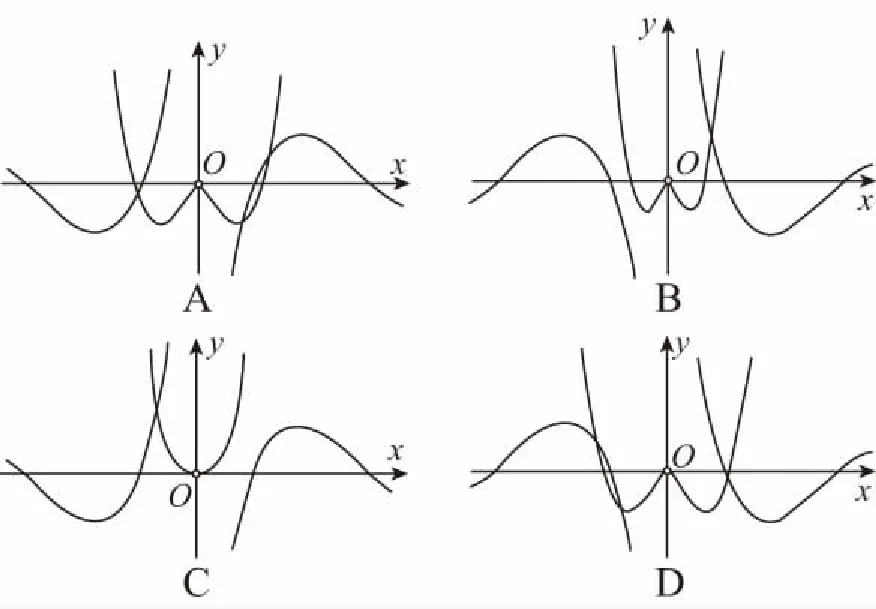
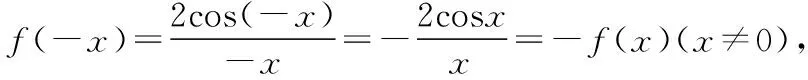
因为g(-x)=(-x)2ln(-x)2=g(x)(x≠0),
所以g(x)是偶函数.
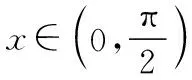
当x∈(0,1)时,g(x)<0.结合选项判断,选项B正确.
【小结】本题通过函数解析式判断函数图象,考查了函数的奇偶性,也考查了数形结合思想.
【例2】如图,正三角形ABC内的图形来自中国古代的太极图.正三角形内切圆中的黑色部分和白色部分关于正三角形的中心成中心对称.在正三角形内随机取一点,则此点取自黑色部分的概率是
( )
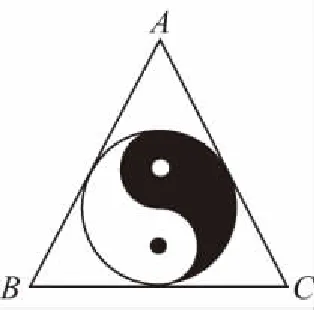

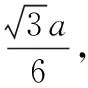
【小结】本题以太极图为背景考查几何概型的概率计算公式的运用,改编自2017年的高考题,考查了数学文化、数形结合思想,识图、用图的能力.
考查函数方程思想的题目:

( )
A.(-∞,-1]∪[2,+∞)
【解析】g′(x)=2a(cosx-sinx)-4a,


因为sin2x-1=-(sinx-cosx)2,
所以(sinx-cosx)2-2a(sinx-cosx)-4a≤0.


令t=sinx-cosx,
则设h(t)=t2-2at-4a(-1≤t≤1),
若要f(x)≥g′(x)恒成立,
即h(t)≤0(-1≤t≤1)恒成立,

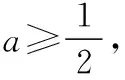
【小结】本题考查导数的计算,通过换元、构造新函数、由不等式恒成立求参数的取值范围,是一道常考题,也是重点题型.
考查分类讨论思想的题目:
【例】已知函数f(x)=aex(ex+1)-4ex-2x.
(1)若a=0,求f(x)在P(0,f(0))处的切线方程;
(2)若f(x)有两个零点,求实数a的取值范围.
【解析】(1)当a=0时,f(x)=-4ex-2x,
所以f′(x)=-4ex-2,
所以f(0)=-4,f′(0)=-6,
所以f(x)在P(0,f(0))处的切线方程为y+4=-6x,
即y=-6x-4.
(2)f(x)=aex(ex+1)-4ex-2x,
则f′(x)=a[ex(ex+1)+ex·ex]-4ex-2=2ae2x+(a-4)ex-2=(aex-2)(2ex+1),
当a≤0时,f′(x)<0,
则f(x)在R上单调递减,不可能有两个零点,舍去;

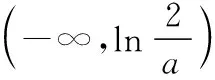
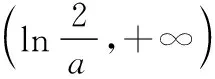
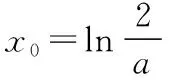
当x→+∞时,y→+∞;
当x→-∞时,y→+∞,

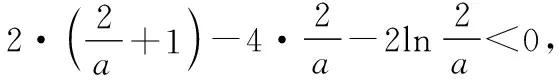
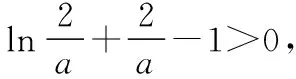
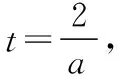
【小结】本题型是高考必考题型,考查导数的几何意义、导数的运用、函数的零点,通过函数的零点个数考查分类讨论思想以及综合运算求解的能力.
考查等价转化思想的题目:
【例】已知函数f(x)=|x-3|+|x-4|.
(1)若f(x) (2)记m为f(x)的最小值,且正实数a,b,c满足a+b+c=m, 【解析】(1)由题意知,f(x) 则f(x)≥a在R上恒成立,即a≤f(x)min. 由f(x)=|x-3|+|x-4|≥|(x-3)-(x-4)|=1, 可得f(x)min=1,所以a≤1. ≥2(a+b+c)=2. 【小结】本题通过绝对值三角不等式、基本不等式求最值,考查了等价转化思想在解题中的运用. 难度是试卷评价中最为敏感的指标,恰当的把握试题的难度是命题的基本要求,高考类试题的难度系数一般在0.6左右,试题难度大,想说爱你不容易.试卷难度的把握至少应做好两个方面的工作:①合理预估试题难度;②比例分配. 影响试题难度的要素:①试题的指示词、材料、情景对解题的提示程度;②试题提问的角度与措辞;③题目阅读量的多少;④正确答案的清晰程度(或错误答案的迷惑程度);⑤书写量的大小;⑥解题的思维品质与思维量的大小;⑦解题的繁简程度. 试题的区分度是指考试题目对学生心理特征的区分能力.区分度高的试题能将不同水平的学生区分开来,水平高的学生得分高,水平低的学生得分低.某一分数区间的分数相对集中、高分太多、不及格的太多,都说明区分度低. 区分度是指试题或试卷对学生实际水平的区分程度和鉴别能力,是反应学生差异的指标.理想的数学考试应是“平均分高、区分度好”,打磨细节还包括答案及评分标准的设置,考查知识点不超出“考试说明”“学科指导意见”中所规定的内容,情境新,考查的能力是考生必备的. 一份优质的试卷从美学角度应叙述简明、通俗易懂、表述规范、没有歧义、符号准确、图文并茂.绝不允许使用含糊其辞、模棱两可的语言.有时在可能会出现误解和忽略的地方,还可标上着重号,以作强调. 试题答案注重通性通法、一题多解可以使所学的知识活化,融会贯通,开拓思路,通过一题多解,分析比较,寻找解题的最佳途径和方法,能够培养发散思维和创新思维能力,有利于优化思维品质,从而达到提高学生的学习兴趣、学好数学的效果. 【例1】∀x∈(0,π),tanx<1的概率为 ( ) 【解析】本题考查正切曲线的简单性质及长度型几何概型的概率的求法. ( ) C.4 D.2 【解析】本题考查解三角形、正弦定理、余弦定理. 综上所述,原创研发、编制全真卷是一项科学性、技术性和程序性都很强的工作,需要团队各个成员的积极支持与配合,在试卷的难易性、整体性、原创性、创新性、信息性、预测性、科学性、严密性上狠下功夫,确保细目明确、难度适中、区分适度、原创有味、闪耀思想.
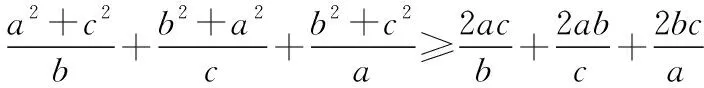
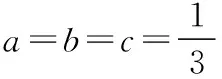
三、难度适中、区分适度
四、答案整齐规范、注重一题多解