2017年课标全国卷平面向量题源分析及2018年复习策略探究
云南 唐明超
1.平面向量考题分析与母题探源
1.1考查数量积的坐标运算与夹角
(1)(2017·全国卷Ⅰ文·13)已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=______.
(2)(2017·全国卷Ⅲ文·13)已知向量a=(-2,3),b=(3,m),且a⊥b,则m=______.
母题(新课标人教A版必修四119页A组题12题)已知a=(1,0),b=(1,1),λ为何值时,a+λb与a垂直?
试题分析:两题均考查数量积的坐标运算与性质,侧重考查利用数量积解决向量垂直问题;与课本母题如出一辙,充分体现出高考命题源于课本的规律性.考查基础知识:对任意两个非零向量a与b,有a∥b⟺x1y2=x2y1;a⊥b⟺a·b=0⟺x1x2+y1y2=0;a±b=(x1±x2,y1±y2),a2=|a|2,a·b=|a|·|b|cos〈a,b〉.
1.2考查数量积的定义与模
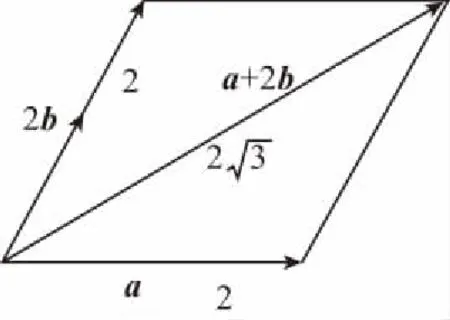
(1)(2017·全国卷Ⅰ理·13)已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=______ .
(2)(2017·全国卷Ⅱ文·4)设非零向量a,b满足|a+b|=|a-b|则
( )
A.a⊥bB.|a|=|b| C.a∥bD.|a|>|b|
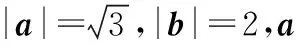
母题(2)(新课标人教A版必修四91页A组题8题)已知a,b为两个非零向量,(1)求作向量a+b及a-b;(2)向量a,b成什么位置关系时,|a+b|=|a-b|(不要求证明).
母题(3)(新课标人教A版必修四120页B组题3题)已知向量a,b,c,d为非零向量,且a+b=c,a-b=d,求证:|a|=|b|⟺c⊥d,并解释其几何意义.
母题(4)(新课标人教A版必修四120页B组题2题)已知向量a,b为非零向量,求证:a⊥b⟺|a+b|=|a-b|,并解释其几何意义.
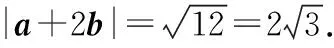
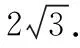
试题(2)分析:(法1:公式法)由|a+b|=|a-b|平方得|a|2+2ab+|b|2=|a|2-2ab+|b|2,即a·b=0,则a⊥b,故选A.
(法2:几何法)利用平行四边形法则作出a+b,a-b,据题意可得该平行四边形为矩形,从而得出正确答案.
考点分析:平面向量中涉及有关模长的问题,通法是将模平方,利用数量积公式进行处理,很容易得出答案;另外,向量是解决数学问题的一个重要工具,具备代数和几何特征,解决此类问题可以利用数形结合的思想,能提高解题效率.复习过程中只要能准确掌握处理母题的基本思想方法,掌握基本原理,对此类高考题的解答就会显得很自如.
1.3 借助坐标系化繁为简
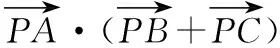
( )
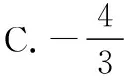
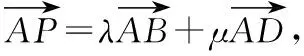
( )
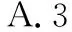
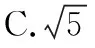
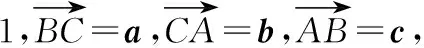
( )
A.3 B.-3
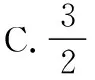
试题(1)分析:(坐标系法)依题意以BC为x轴,BC的垂直平分线AO为y轴,O为原点建立平面直角坐标系如图所示,

试题(2)分析:(坐标系法)如图所示,建立平面直角坐标系:
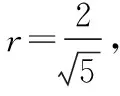
母题(1)分析:利用数量积定义,向量的模长已知,故只需确定其夹角即可,由向量夹角定义得向量a与b的夹角为120°,向量b与c的夹角为120°,向量c与a的夹角为120°.
考点分析:以上两题重点考查平面向量的坐标运算、函数最值的求解方法.平面向量中有关最值问题的求解通常有以下两种思路:一是利用平面向量的几何意义将问题转化为平面几何中的最值或范围问题,然后根据平面图形的特征直接进行判断,充分体现化归的数学思想;二是利用平面向量的坐标运算,把问题转化为函数的最值或值域、不等式的解集、方程有解等问题,然后利用函数、不等式、方程的有关知识来解决,充分体现函数与方程的思想.但是如果能正确建立平面直角坐标系,利用坐标运算实现转化,从而由函数的性质得出结论是较为简单的.而母题选用的是正三角形,根据正三角形的三线合一这一特殊性质,容易建立平面直角坐标系,从而实现求解;就较基础的题目而言,相比基底法与投影法,坐标系法的优越性体现得不是很明显,但是对于相对较复杂的题目,由于思维难度相对较高,此时合理利用坐标系法可以很快解决问题.
1.4课标卷考点综合解读
结合近几年课标卷高考试题,发现平面向量这一章节的命题呈现以下规律:从考查题型看,一般会设置2个客观题;从考查分值上看,约占10分,主要考查对基础知识,基本运算,基本方法的掌握;从考查的知识点看,主要考查平面向量的线性运算,平面向量基本定理,数量积的运算及其性质,包括夹角,模及垂直;重点考查数形结合,函数与方程,化归的数学思想.从命题思路来看有以下几个方面:首先,结合三角形,平行四边形等基本模型考查平面向量的线性运算;其次,结合坐标运算考查平面向量的共线与垂直,再者,结合向量的模,夹角等知识考查平面向量的数量积;最后,在知识交汇点处命题,往往结合向量与三角函数、解析几何等综合考查应用能力.
2.2018年复习策略探究
2.1回归教材,夯实双基
根据以上的命题特点及规律,复习本章时,要注意以下几个方面:(1)要做到准确理解知识的本质,要重视对相关概念,定理的理解和掌握,如:相等向量,相反向量,单位向量,共线向量基本定理,平面向量基本定理,向量的模、夹角以及向量的数量积.(2)重视对运算法则及相关公式的理解与应用,如线性运算,数量积的相关运算公式.(3)注重解题方法和解题规律的总结与优化.(4)重视数学思想方法的应用,平面向量中蕴含着十分丰富的数学思想方法,这也是高考必考的原因.
2.2吃透教材例题及习题,注重变式探究
高考题,特别是对本部分知识点的考查,立足教材,适当变形,适度整合,渗透数学思想是高考命题的常态,所以,万变不离其宗,研究课本例习题就显得尤为重要.
2.3跳出题海,高瞻远瞩,培养核心素养
高考复习,一定量的练习是必要的,但是不能陷入题海,要注重一题多解与多题一解的学习实践,所以要养成变式思维,注重对经典题目的变式练习.另外通过对经典例题的研究与变式,不断提高数学抽象能力,逻辑推理能力,数学建模能力和数学运算能力.
3.课本母题变式举例
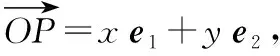
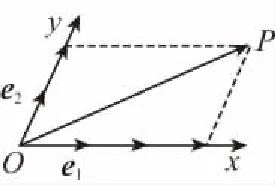
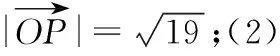

改编意图:旨在充分理解并运用平面向量基本定理,会线性表示平面上的任一向量,重点体会化归的数学思想和函数与方程的思想,学会灵活运用数量积这一工具解决平面几何的相关问题.
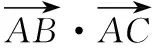
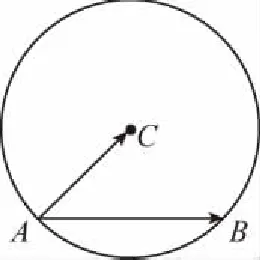
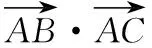
( )
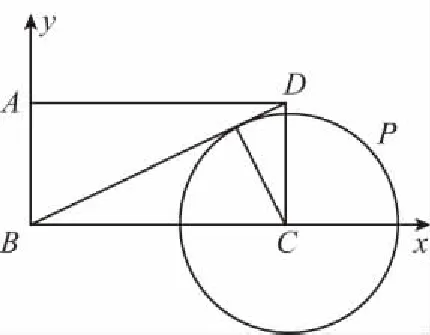
①半径r②弦AB的长 ③∠BAC④∠BCA
改编意图:适当改变题目的问法,保证已知条件不变,题目的难度和深度加大了,这对平时的复习很有意义,母题重在考查平面向量数量积的几何意义,而变式1不仅考查数量积的几何意义,同时也考查了正、余弦定理.
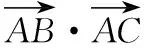
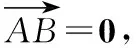
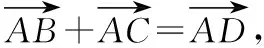
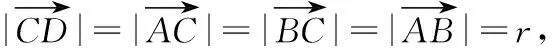
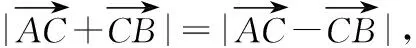
改编意图:受变式3的启发,条件加强,立马可以得出△ABC为等腰直角三角形.

