透析教材习题 串接高考亮点
——对一道解三角形题目的再思考
广东 杨伟达
高考试题源于教材,又高于教材.纵观近几年高考数学题,许多高考试题在教材中都有呈现,进而找到了试题的“活化石”.因此,回归教材就是在高考题中找到教材中的“活化石”,感悟着“活化石”带来的数学味道.
一、题目再现
题目(高中人教版必修5 P18练习第2题) 一块四边形土地的形状如图所示,它的三条边的长度分别是50 m,60 m,70 m,两个内角是127°和132°,求四边形的面积(精确到0.01).
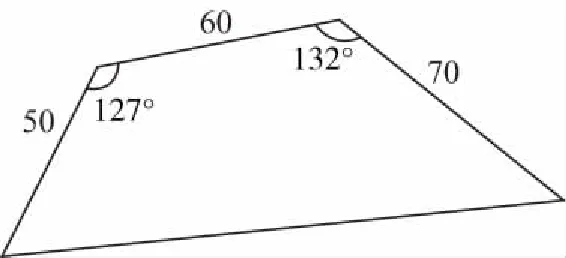
分析这是一道生活中的数学题,在翻阅教材时引起了笔者的注意,于是捡回了此题,查阅教师教学用书,可在教参里只提供了答案,没有详细的解答过程,或许该题运算繁杂、方法复杂,或许是练习题的缘故,没有引起师生重视.对此笔者感到在生活中数学无处不在,加上解决此题的思想、方法来自生活实践,觉得很值得探讨.
二、解法探究
思路一(分割+正、余弦定理)
分析对于这样的不规则的四边形,没有直接计算面积的方法,于是采用分割法把四边形分成两个三角形,分别求出两个三角形的面积,以和的形式求得四边形的面积.
解法1如图,连接AC,
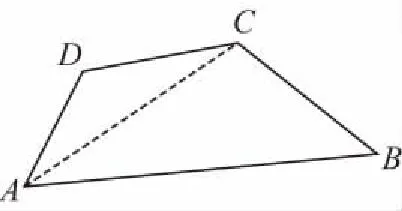
在△ADC中,根据余弦定理得
AC2=AD2+DC2-2AD·DC·cos∠ADC
=502+602-2×50×60×cos127°
≈9 710.89,
所以AC≈98.54 m.
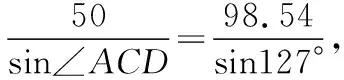
求得sin∠ACD≈0.405 2,
所以∠ACD≈23.9°(锐角),
因为∠ACB=132°-∠DCA=132°-23.9°=108.1°,
所以S四边形ABCD=S△ACD+S△ACB
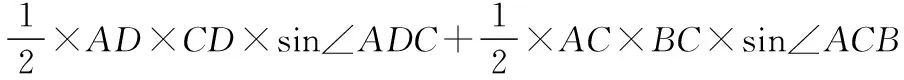
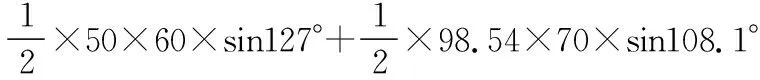
≈4 476.19 m2.
思路二(补形+正弦定理)
分析对于这样的不规则的四边形,没有直接计算面积的方法,于是采用补形法把四边形补角还原成一个大三角形,分别求出两个三角形的面积,以差的形式求得四边形的面积.
解法2如图,∠ADC,∠DCB分别是△DEC的外角
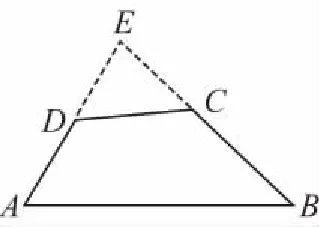
因为∠ADC=127°,∠DCB=132°,
所以∠EDC=53°,∠ECD=48°,
所以∠E=180°-∠EDC-∠ECD
=180°-53°-48°
=79°,
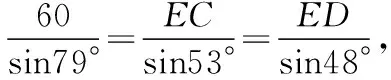
解得ED≈45.42 m,EC≈48.81 m,
所以EA≈95.42 m,EB≈118.81 m,
所以S四边形ABCD=S△EAB-S△ECD
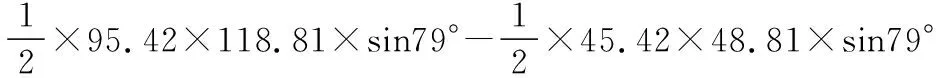
≈4 476.17 m2.
思路三(向量数量积+正弦定理)
分析对于这样的不规则的四边形,没有直接计算面积的方法,因题设给出了两角和三边,采用向量法求出该四边形的另一边长,再分别求出两个三角形的面积,以和的形式求得四边形的面积.
解法3依题可知,如图,在四边形中,
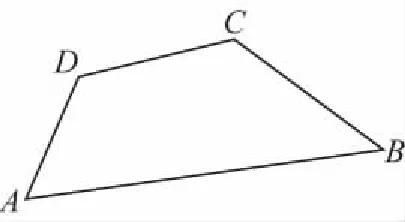
∠ADC=127°,∠DCB=132°,
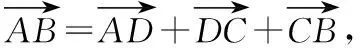
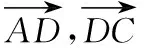
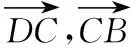
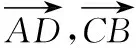
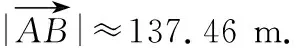
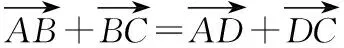
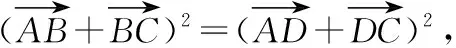
即502+602-2×50×60×cos127°=137.462+702-2×137.42×70cos∠B,
解得∠B≈42.96°,
所以S四边形ABCD=S△ACD+S△ACB
≈4 476.65 m2.
三、解后反思
由于高中数学必修5第一章第二节练习第2题是生活中的数学,是现实生活中的实际情况,却因题设条件的数值不是特殊数值,往往需要用计算器,所以给学生带来不少运算困难.其次,笔者发现用计算器算出答案与教材给出的答案有小小误差.究其原因,笔者在每步运算中取小数点后两位数导致的,所以存在误差是正常的.再次,解决此问题的思想、方法来自生活中的实践经验.一种是分割思想;另一种是拼图(补形)思想.归根到底就是回归到最简单、最基本的图形——“三角形”中.对这样一个“不起眼”的练习题,笔者在教学上做了两种方式处理:一种方式强调以学生为主,在讲学稿上做文章,降低难度,减少运算量,修改条件,使题目更接“地气”,更接近学生的思维水平;另一种方式强调学生的学习过程,教师在讲授新课后布置作业给学生,让学生慢慢体验其学习过程,突显学生掌握知识的深刻性.这往往需要学生在熟练掌握三角形的正、余弦定理基础上,灵活运用这些定理解决实际生活问题.
1.优化条件
美国教育心理学家奥苏贝尔说过:“影响学习最重要的原因是学生已经知道了什么,我们应当根据学生原有的知识状况进行教学.”因此,数学问题要找准学生学习的最近发展区,才能架起学生现有情况与潜在发展水平之间的桥梁,寻找属于他自己的解题策略.这就要求教师对数学问题进行适当的优化.
优化策略一、把条件的数值改为特殊值,便于运算.
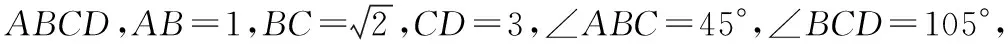
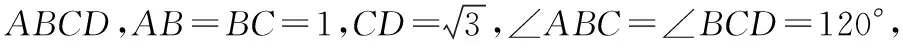
优化策略二、减少某一条件,将设问部分改为最值问题.
本题从方程的角度考虑,常见“知三求一”“知二求一”.因此,笔者试图尝试减少某一条件,将设问部分改为最值问题.此时原问题就变为函数问题,更改后难度增大.
【变式三】四边形ABCD,AB=1,CD=2,∠ABC=∠BCD=60°,问:当BC边长取何值时,四边形ABCD的面积最小,最小值为多少?
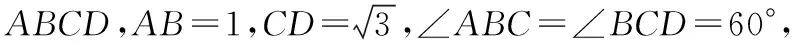
2.把握方向
通过教材练习题的学习,加深了对三角形正、余弦定理的理解和掌握,提高了学生的分析问题、解决问题的能力,从而驾驭一些高考试题就会得心应手.
策略一、链接高考考究真题
例1(2015·全国卷理·16)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是______ .
分析求解此题的方法:回归到三角形中.用传统方法处理,作辅助线把四边形分为两个三角形,设未知量,用正弦定理求解,运算复杂,学生只能望而止步;用极端思想处理,在保持题目条件不变的情况下,平移AD,就会变为两个特殊的三角形,再用正弦定理可求得AB的极端值.这样运算简便、快捷.
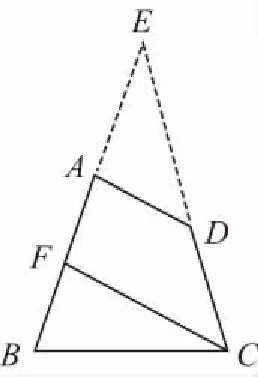
解动态审视(1)四边形ABCD,保持BC=2及∠B=∠C=75°固定,延长BA,CD交于E,平移AD,此时当A与D重合于E点时,AB最长.
在△BCE中,∠B=∠ECB=75°,∠E=30°,BC=2,
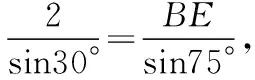
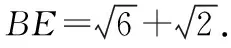
动态审视(2)四边形ABCD,保持BC=2及∠A=∠B=75°固定,平移AD,当D与C重合时,此时与AB交于F,AB最短.
在△BCF中,∠B=∠BFC=75°,∠FCB=30°,
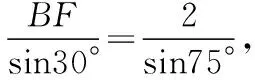
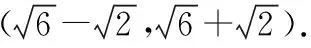
策略二、模拟高考贴近生活
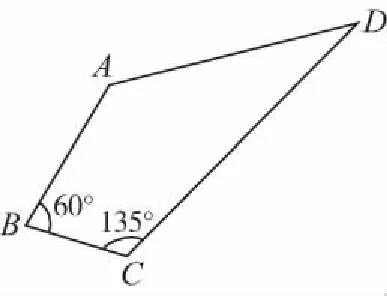
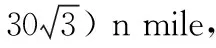
分析本题涉及航程问题.四个城市A,B,C,D可组成一个四边形ABCD,其实是解三角形的应用问题.解决此问题涉及多次用到正、余弦定理、勾股定理,运算繁杂,难度较大.先算AC,再求得cos∠ACD,然后算AD,再求∠CAD,最后求得EC.
解设轮船航行到E点时改向城市C直线航行.
连接AC,EC.依题可得AE=50,
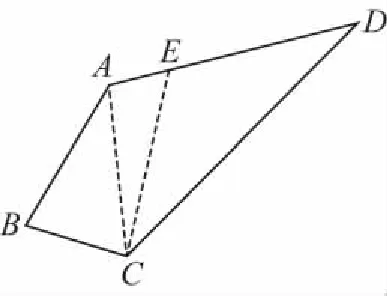
在△ABC中,∠ABC=60°,AB=80,
则AC2=AB2+BC2-2AB·BC·cos∠ABC,
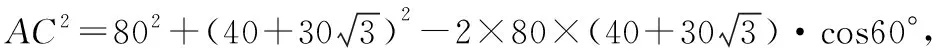
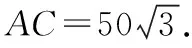
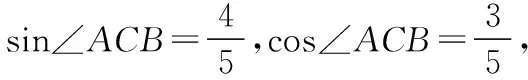
又因为∠BCD=135°,
所以∠ACD=135°-∠ACB,
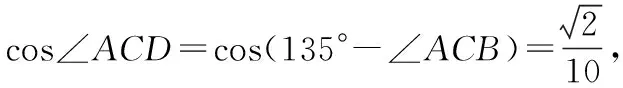
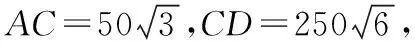
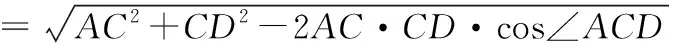
所以AD2+AC2=CD2,
所以△ACD为直角三角形,∠CAD=90°,
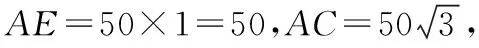
其实,许多多边形(包括四边形)都是在三角形基础上“砍角”形成的.因此,回归三角形是解决有关多边形的常用方法.同样,有关四边形的数学问题可以通过“分割”和“补形”回归到三角形中,再运用三角形正、余弦定理,从而达到对问题的求解.
四、结束语
总之,教师一方面要深刻领悟教材编写者的意图;另一方面又不能拘泥于教材,在课堂教学中要敢于突破教材,进而对教材再创新,赋予教材新的活力.

