新课标高考立体几何的考点分布及解法探析

宁夏 张 兴 朱全林

立体几何在人们生活、生产建设中有广泛的应用，是高中数学的必学、必考内容，从近十年高考试题的考点分布既可以看出命题的发展变化趋势，又能发现目前考题的热点和未来可能要考查的边缘知识点，所以研究立体几何试题的呈现特点及其解答方法，不但可以帮助学生学好这部分知识，提高成绩，更重要的是能够提高学生的数学核心素养.

一、试题考点分布统计

新课标从2007年开始到2017年文、理共计36套题，其难度基本属于中、低档题目，注重考查基本几何体的结构特征、几何元素之间的位置与数量关系、体积和面积等，主要考查学生空间想象能力、推理论证能力、转化与化归能力和运算求解能力.文、理科试题的选材背景基本一致，只有解答题第二问的能力要求层次略有不同.文、理科客观性小题共计72道，解答题36道.其中涉及几何体综合解答题36道，三视图的30道，球与其他几何体的组合体27道，体积、面积、角和距离计算的8道，判断空间元素位置关系的有7道，发现文、理科均有2个小题和1个大题，小题以三视图和球的组合体为主，大题以正、直多面体为背景，具体包括证明垂直与平行关系、计算体积和面积、求二面角的平面角或直线与平面所成的角三大类.总的来看依据考纲，面面俱到，紧扣考纲，注重基础，多次考查被遗忘的内容.

二、典型例题解法探析

题型一、空间几何体的三视图与直观图

【例1】(2017·全国卷Ⅰ理·7)某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为

( )

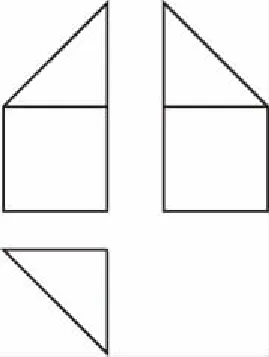
A.10 B.12

C.14 D.16

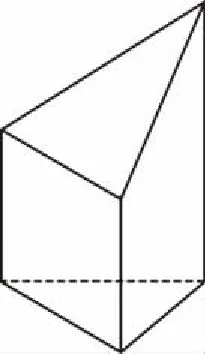
【解析】由三视图可画出立体图如图所示，该立体图各个面中只有两个相同的梯形的面，S梯=(2+4)×2÷2=6，S全梯=6×2=12，故选B.

【探析】本例由三视图构建直观图，然后利用给出的数量，计算出梯形的面积之和.这类题型近十年出现30道，它主要考查三视图及其相关知识、技能的掌握与运用，指向于学生的空间想象能力，识图、构图及其动手操作能力，计算求解能力.解答这类题：第一，要让学生掌握三视图的基本概念及特征；第二，熟练掌握常见基本几何体的三视图与直观图的结构特征；第三，掌握由三视图构建直观图的程序化步骤，即俯视图定下底面、正视图结合侧视图定上底面、综合建构直观图；第四，能够把三视图的数量转化为直观图中的数量，再完成题目要求的计算.

题型二、球与多面体或旋转体的组合体

【例2】(2016·全国卷Ⅲ理·10)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球，若AB⊥BC，AB=6，BC=8，AA1=3，则V的最大值是

( )

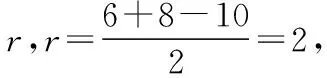
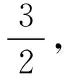
题型三、空间元素位置关系的定性判断

【例3】(1)(2017·全国卷Ⅲ理·16)a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：①当直线AB与a成60°角时，AB与b成30°角；②当直线AB与a成60°角时，AB与b成60°角；③直线AB与a所成角的最小值为45°；④直线AB与a所成角的最大值为60°，其中正确的是________.(填写所有正确结论的编号)

( )

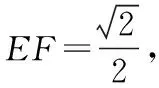
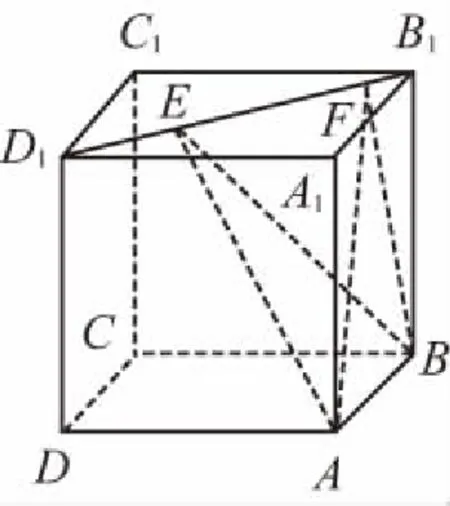
A．AC⊥BE

B．EF∥平面ABCD

C．三棱锥A-BEF的体积为定值

D．△AEF的面积与△BEF的面积相等

【解析】(1)构造如图正方体，用EB表示a,BD表示b,当B在边BD上从D到B运动时，就会发现Rt△ABC位于Rt△ADC位置时，AB与BD垂直、与EB成45°角，从D到B沿直线DB运动时，AB与BD所成的角在减小、与EB所成的角在增大，就会发现居于Rt△ABC位置时两角相等且为60°角，故选②③.

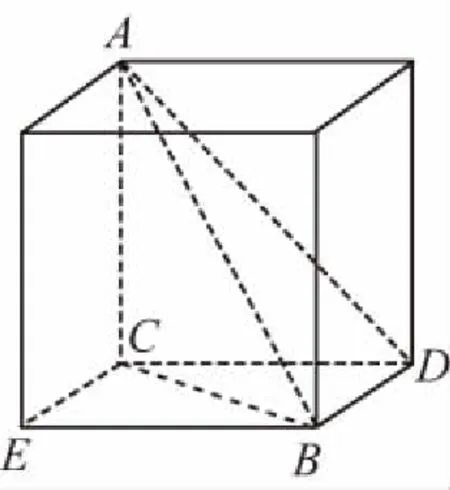
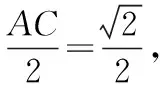
【探析】本例(1)构建空间模型，在点、线的运动变化过程中逐步确定答案；(2)运用空间元素位置关系的定义、公理和定理，结合具体的数值计算确定答案.这类题近十年共出现了7道，主要考查学生的空间想象能力、逻辑思维能力和分析解决问题能力.解答这类题：第一，要从整体的角度把握构成基本几何体上的线、面的结构特征.第二，要熟练掌握空间内直线与平面各种位置关系的定义、判定、性质及其特征，能够在几种平行或垂直关系间进行转化和化归.第三，在具体判断位置关系时，有两种思路，一种是用概念、公理和定理去检验，排除不适合条件的选项而确定答案；另一种是构建空间模型在图形的动态演示中，获取正确的答案.

题型四、有关长度、距离、角度、面积和体积等问题的定量计算

【例4】(2017·全国卷Ⅱ理·10)已知直三棱柱ABC-A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，则异面直线AB1与BC1所成角的余弦值为

( )

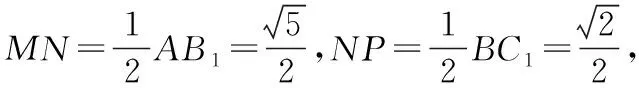
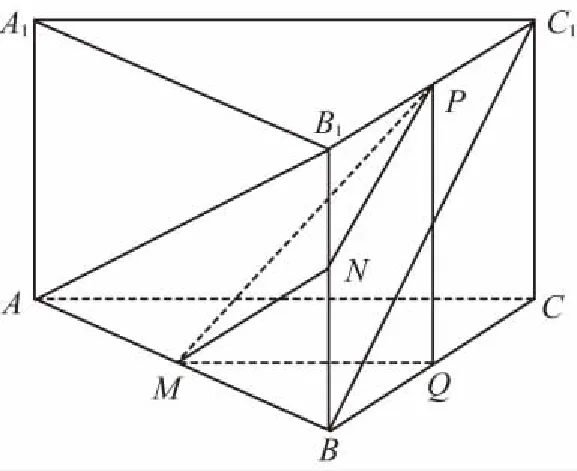
【探析】本例求异面直线所成的角，采用平移法构造三角形，计算三边长，用余弦定理求夹角，是教材要求掌握的最基本方法.像这类求异面直线所成的角、直线与平面所成的角、点面距、面积和体积的客观性小题近十年出现了7道，它侧重于考查“三基”.解答这类题：第一，要加强对立体几何本质(大小、形状和位置)的理解，掌握长度、距离、角度、面积和体积的相关概念和公式；第二，要重视通性通法的训练，特别是平移法、体积法、向量法、变换视角方位法等.

题型五、正或直多面体的综合解答题

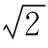
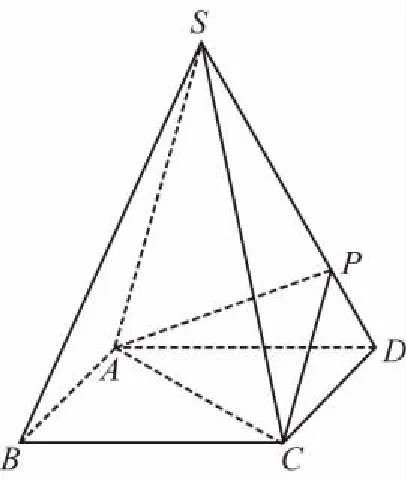
(Ⅰ)求证：AC⊥SD；

(Ⅱ)若SD⊥平面PAC，求二面角P-AC-D的大小；

(Ⅲ)在(Ⅱ)的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC.若存在，求SE∶EC的值；若不存在，试说明理由.

【解析】解法一：(Ⅰ)连接BD，设AC交BD于O，由题意SO⊥AC.在正方形ABCD中，AC⊥BD，所以AC⊥平面SBD,得AC⊥SD.

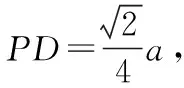
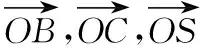
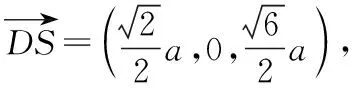
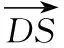
【探析】本例以正四棱锥为载体，考查空间内线面平行关系的转化和二面角的平面角.其中(Ⅱ)可以用定义法即一作二证三计算处理，也可以建立空间直角坐标系，用向量的夹角公式进行计算.(Ⅲ)为探索性问题，重在考查学生分析和解决问题的能力.

【例5】(2014·全国卷Ⅱ文·18)如图，四棱锥P—ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.

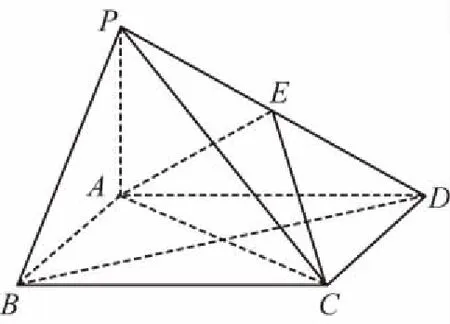
(Ⅰ)证明：PB∥平面AEC;

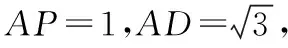
【解析】(Ⅰ)设BD与AC的交点为O，连接EO.因为ABCD为矩形，所以O为BD的中点.又E为PD的中点，所以EO∥PB，EO⊂平面AEC，所以PB∥平面AEC.

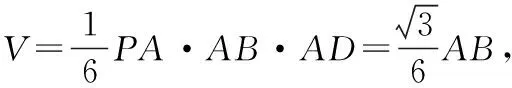
【探析】本例以有一条侧棱垂直于底面的四棱锥为载体，考查空间内线面平行关系的转化与化归，以及运用体积法求点面距.

【例6】(2017·全国卷Ⅲ理·19)如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．

(Ⅰ)证明：平面ACD⊥平面ABC；

(Ⅱ)过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D-AE-C的余弦值．

【解析】(Ⅰ)由题设可得，△ABD≌△CBD,从而AD=DC.又△ACD是直角三角形，所以∠ADC=90°.取AC的中点O，连接DO,BO,则DO⊥AC,DO=AO.

又由于△ABC是正三角形，故BO⊥AC.所以∠DOB为二面角D-AC-B的平面角，在Rt△AOB中，BO2+AO2=AB2.又AB=BD，所以BO2+DO2=BO2+AO2=AB2=BD2，故∠DOB=90°,故平面ACD⊥平面ABC.

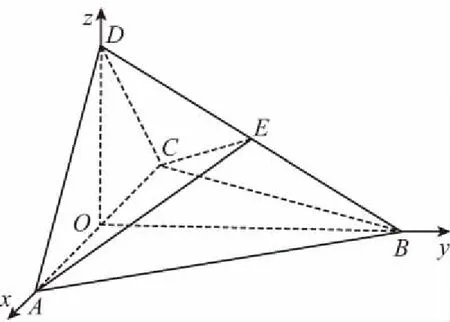
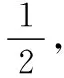
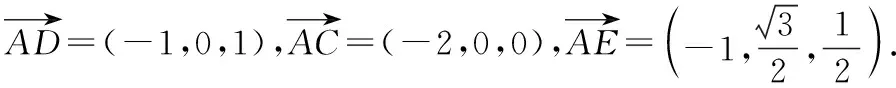
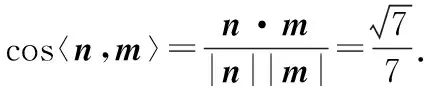
【探析】本例以底面为正三角形的三棱锥为载体，考查空间内线面垂直关系的转化与化归，运用逻辑推理在已知条件下不难得出.同时考查二面角的基础知识，在建立空间直角坐标系之后，运用向量的夹角即可求出.

近十年高考立体几何综合解答题类似于上述例4、5、6，均为常见几何载体，其中锥体23个，主要包括三棱锥和四棱锥；线体5个(上底为一条线，包括平放的三棱柱)；正方体8个.这些几何体有两大特征，其一“正”即有正三角形或正方形的面；其二“直”即侧棱垂直底面、侧面垂直底面或直多面体.这些特征是解答题的基本切入点，“正”为定量问题，其中必有相等关系；“直”为定性问题，其中必有垂直关系，而且垂直关系为建立空间直角坐标系埋下伏笔，为利用向量解答提供的了可能.出现的问题有四大类，其中涉及垂直关系的21道，与体积相关的问题17道,涉及二面角的平面角的15道，涉及平行关系的12道，文科以体积问题为主，理科以二面角的平面角为主.主要考查空间内线面位置关系以及二面角和体积的计算，指向学生空间想象能力、逻辑推理能力和运算求解能力.在正或直多面体的综合解答题教学中：第一，要重视“三基”的掌握；第二，重视典型例题的教学;特别地，要注意运用逻辑知识分析例题内容，探查已知和未知之间可能存在的因果链接，准确表述逻辑过程.

三、教学建议

1.夯实知识基础，构建立体网络化的知识结构

要从整体的角度把握几何体的空间结构特征，对于其上的点、线、面位置关系要有深刻的认识.尤其在例题教学中要突出线线、线面和面面三类几何元素关系的本质特征，即它们分别处于平行、相交、垂直时的定量特征与定性特征，强调知识之间的内在逻辑联系.重视例题教学后的类化、变化和归化，这样可以由点及线、由线及面，形成知识之间网络化的逻辑结构.如“欲证线面平行，只需线线平行”变化之后就是“欲证面面平行，只需线面平行”；归化之后就是指“线面关系退一步变为线线关系，进一步变为面面关系”.明确了线面关系在线线、线面和面面关系中的核心地位，这样证明线线平行、面面平行也就有了方向和思路.

2.强化空间观念，培养学生空间想象和思维能力

要从直观感知开始发展学生的空间观念，让学生通过观察实物模型、动手做几何模型、多媒体课件等进行直观感知，在直观感知的基础上发展理性思维.在例题教学中要重视识图、画图和用图能力的培养，要让学生能够画出空间几何体的三视图与直观图，并能在二者之间进行无障碍的转化.要引导学生从不同的角度去观察和分析几何体的特征，拓展学生视野，培养空间想象和思维能力.

3.重视思想方法教学，提高学生的解题能力

数学思想方法是数学知识的灵魂，对数学思想方法的把握是数学素养的体现.在教学中重视函数与方程思想的培养，要在几何元素的运动变化过程中，分析具体问题所包含的变量关系，也可以在空间线、面的动态演示中获取答案，如上述例3(1).要把立体几何中的数学公式当作方程运用，把几何问题中的最大、最小化问题转化为函数的最值进行处理，如上述例2.这些都是立体几何创新试题着陆点.在教学中要突出化归与转化的思想培养，如平行与垂直关系的转化、空间平面化、几何向量化等，要能够借助于数学知识和方法，将给出的问题化难为易、化繁为简、化生为熟，将抽象问题具体化，把等待解决的问题化为一个成熟的、能解决的问题.

4.突出“两法四题型”，在解题训练中提高素养

对计算距离、长度、角度、面积、体积等问题的通性通法要熟练掌握.“两法”即向量法和综合法.向量法解决立体几何解答题，实现了几何问题代数化，降低了构造图形和推理论证的难度，更有利于问题的解决，而且解答过程具有程序化的步骤，便于掌握，每年的解答题，几乎都可以用.综合法是数学推理论证的主要方法，对于培养学生逻辑推理能力具有非常重要的意义，它的“一作二证三计算”解题模式要牢牢掌握.重视“四题型”的训练，即垂直与平行关系的证明、二面角的求法、球的组合体中的计算、三视图还原直观图再计算体积或表面积.