如何编制初中数学总复习双向细目表

南京师范大学盐城实验学校 孟新明

复习在初中数学教学中占有至关重要的地位，它既能够使学生巩固课堂所学的知识，还能够培养学生的数学综合思维能力，为将来高中数学学习打下坚实的基础。但笔者通过自己的调查研究和课堂实践发现，还是有教师对复习教学的理解存在偏差，有些教师片面地将数学复习简单地理解为让学生去做题；在复习题的基础知识、综合运用和拓展延伸方面抓不住考点要求，把握不住考点的深浅；对复习题的教学要求把握不够。因此，研究和编制双向细目表已成为聪明的教学管理者和教师用以探寻统考试卷在“考什么”和“怎么考”方面的大致规律，从而探得复习迎考的有效途径。

双向细目表是一种考查目标和考查内容之间的关联表，最初用于命制试题时，根据考试的目的和要求制定的测试内容和目标的具体计划，并以图表形式详细、准确地列出各项内容的量化指标，用以规范、指导考试命题的编题和制卷。当然，双向细目表的类型、难易，因学科门类、课程标准、考试类型、教材版本、教学要求、使用目的等而有所不同。那么，如何编制初中数学总复习的双向细目表呢？本文以“数与代数”中的“绝对值”为例，具体论述。

一、确定考查内容——专题复习双向细目表的纵向编制

双向细目表的制作，必须与国家课程方案、课程标准、考试说明（大纲）以及相关的教学与考试指导意见具体要求相统一。依据中华人民共和国教育部颁布的《义务教育数学课程标准》、“初中数学学科考试说明”和有关省市的“教学与考试指导意见”，把课程内容分为四个部分：数与代数、图形与几何、统计与概率、综合与实践。以“数与代数”中有理数的考查内容中的绝对值为例，我们编制出该专题复习双向细目表的纵向表（参见表1）。

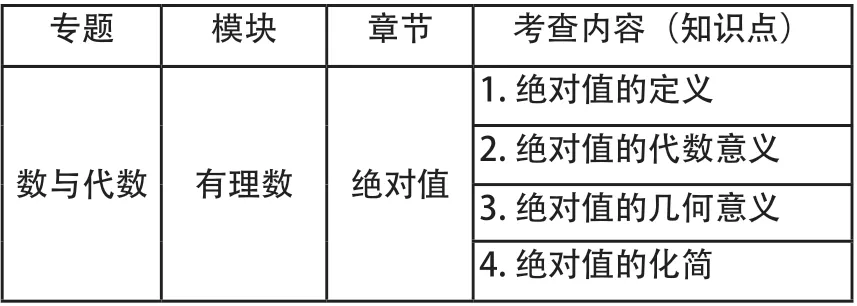
表1 双向细目表的纵向编制（考查内容）

二、确定考查目标——专题复习双向细目表的横向编制

依据课程标准、考试说明（大纲）以及相关的教学与考试指导意见，初中数学课程在知识技能、数学思考、问题解决、情感态度四个方面的具体目标，在《课程标准（2011 年版）》《福建省初中学科教学与考试指导意见·数学》以及江苏省中考数学命题指导意见中，都广泛使用了“经历、体会、感受、体验、探索”等行为动词。从课程标准的要求来看，编制初中数学双向细目表不仅要厘清知识本身，更注重学生的能力层次，所以可以按能力要求水平对双向细目表进行横向设计，这个过程相当于列出教学目标清单。笔者将能力目标从低到高分为七个层次，较高层次的目标包含了较低层次的目标，具体为：了解、理解、掌握、灵活应用、经历、体验、探索。在上述七个目标中，以理解和掌握为主，各个目标应根据课程内容要求和初中生的认知水平与特点加以把握。按能力水平的不同来进行横向设计，这个过程包括：①将能力要求从左到右逐步列出，并将七个能力目标进行细化（如表2 所示）。本文将了解、理解和经历三个层次的能力要求划分为“易”，将理解、掌握、体验划分为“中”，将灵活应用、探索划分为“难”。②复习时根据测试内容和目标要求，用双向细目表来以图表形式详细、明确地列出各项内容，用以规范、指导考试命题的编题和制卷。

表2 双向细目表的横向编制（考查目标）

三、精准定位考点——专题复习双向细目表的合成

编制按知识要点进行纵向设计和按能力水平进行横向设计的“双向细目表”是书面考试科学命题的一个关键环节，也应成为教师梳理教材、研究教学、提高质量的一项基本技能。专题复习双向细目表的合成包含两个步骤：其一，将“表1”与“表2”按纵坐标和横坐标组合起来；其二，确定考查内容与考查目标（能力要求）的交叉点。其中，后者是专题复习双向细目表能否成立的关键，直接关系到我们能否精准定位考点。合成后的初中数学专题复习双向细目表见表3。这里需要特别指出的是，尽管“考点”这个词我们经常用，但是很多老师理解的“考点”其实还是知识点，比如说“绝对值是考点”，这句话其实是不对的，真正的“考点”是考查内容（知识点）与考查目标（能力要求）的交叉点，即对“绝对值”中的“绝对值代数意义”和“绝对值几何意义”的综合运用，由此也体现出数学中的“数形结合”思想、对“绝对值的化简结果”的“验证”和“推论”、“绝对值的化简”和“数形结合”，这才是“考点”。只有这样，编制出的专题复习双向细目表才能较好地把握统考试卷在“考什么”和“怎么考”方面的大致规律，以有效提高复习迎考的针对性。

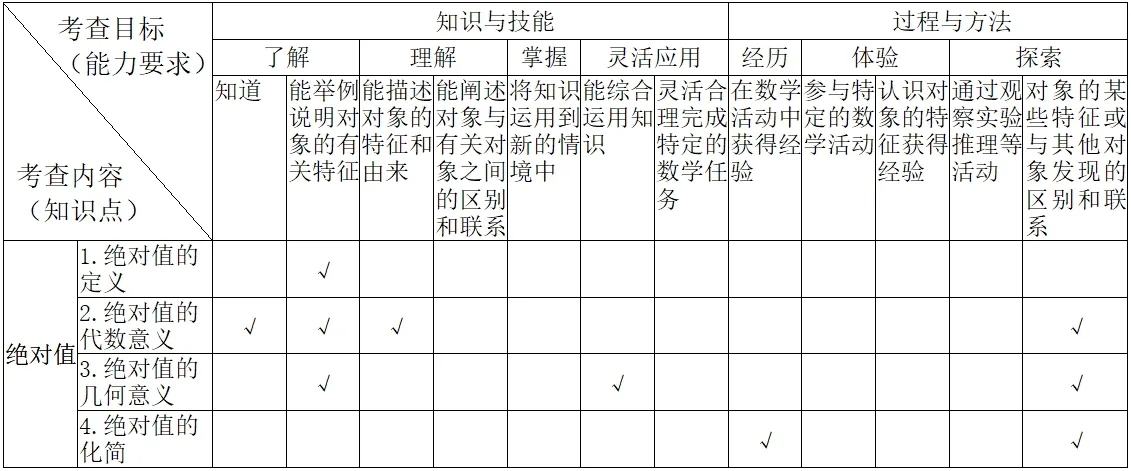
表3 “有理数”的双向细目表