环槽等速传动啮合副磨损补偿平衡研究

于秀涛，姚方方

（黄河交通学院 汽车工程学院，河南 焦作 454950）

1 引言

环槽等速传动机构能够解决摆线钢球行星传动减速啮合副的偏心问题，且能够实时消除啮合副磨损间隙，实现机构的无隙啮合传动，使摆线钢球行星传动成为精密传动中非常重要的高性能传动装置，在精密机械如机器人、机械手、伺服传动机构、航空航天等经常频繁往复工作的传动机构中具有很好的应用前景[1-2]。

国内外学者对安装有环槽等速传动机构的摆线钢球行星传动进行了较多的研究。文献[3-5]对摆线钢球传动结构组成、传动原理、行星运动学分析、齿形综合方法、齿廓曲线解析式等进行了较深入的理论研究。文献[6]在建立理论分析数学模型的基础上，分析了减速啮合副在啮合传动过程中相对滑动速度和滑动率的变化规律，并绘制了变化曲线图；文献[7]建立啮合副两点接触力学模型，推导出机构弹性回差公式，并分析参数对弹性回差的影响；文献[8]用陶瓷球代替钢球进行了相关理论分析与结构设计；文献[9]建立了摆线钢球传动啮合刚度模型，分析了结构参数对啮合刚度的影响规律，并利用摆线钢球啮合副的啮合刚度推导出行星传动部分的等效扭转刚度计算公式。目前为止，尚未有文献对摆线钢球行星传动等速啮合副磨损后的轴向间隙消除（补偿）实现传动机构的精密传动进行研究，未有文献支持机构磨损后能够实现精密传动这一结论。

利用力学中超静定方法，通过变形协调方程和力矩平衡方程推导啮合点法向力计算公式，求得行星盘和输出轴上的啮合点速度以及钢球中心的速度，获得啮合点滑动速度，得到啮合点磨损率计算公式，将每次运行产生的磨损量代入法向力计算公式，获得法向力循环计算公式，并定义法向力变化率和磨损率变化率，以描述啮合副的磨损规律。

2 啮合力计算

受力分析，如图1所示。利用机构转化法，将输出轴固定，行星盘做平动。在输出轴上建立相对坐标系XO1Y，利用力学中超静定的方法，对钢球系加一个顺时针方向的力矩M0，传力接触点法向接触变形为δj钢球系整体转角为Δα0。受力分析，如图1所示。变形协调方程为：

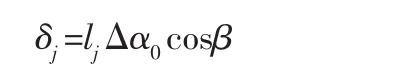
式中：lj＝Rwsinφj

接触点法向力为：Nj＝kg0

式中：kg0—啮合点刚度系数[10]。

图1 受力分析图Fig.1 Force Analysis Diagram

根据行星盘的力矩平衡方程，可得：

式中：Z—钢球数

3 啮合点滑动速度计算

啮合点位置，如图2所示。根据等速机构的平行四边形原理可知，等距线之间的距离必须与输入轴偏心距e相等，才能够实现机构的等速传递。为了保证机构有一定的承载能力，啮合点不在等速线上，啮合点处存在滑动。在对等速机构啮合点滑动速度进行分析时，认为钢球几何中心与理论位置点重合。钢球与输出轴在A点相切，钢球与行星盘在D点相切，Oqj为钢球中心。

图2 啮合点位置图Fig.2 Meshing Point Location Map

钢球几何中心Oqj的切向速度为：

式中：ω—输入轴角速度，ω＝iωc；ωc—输处轴角速度；i—传动比。

输出轴上A点切向速度为：

行星盘上D点的切向速度为：

由以上三个式子可知两啮合点的滑动速度之和为：

由上式和式（2）、式（3）、式（4）联立，可得两啮合点的滑动速度之和为：

啮合点在等速线上啮合副能够实现纯滚动。此时，机构环形槽内侧无法承载，机构不能够实现精密传动。因此，为保证机构的连续传动，啮合点滑动速度之和始终为负值。由于行星盘与输出轴上啮合点处机构形状尺寸相同，则根据滑移理论，认为两啮合点处的滑动速度相同，均为Δv1/2。

4 环槽磨损分析计算

4.1 磨损率计算

磨损深度变化率Δδ′为：

式中：p—Nj名义压力，p=Nj/Sj，Sj名义面积，法向力；E—综合弹性系数；k1—磨损系数；σp—符合标准差；1/Rp—复合平均曲率。

4.2 循环迭代计算

在第n次循环时，接触点法向力为：

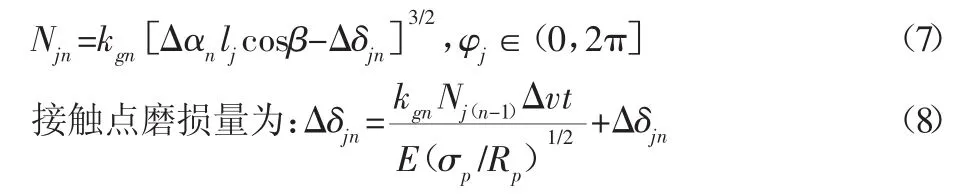
式中：t—次循环内接触点参与磨损时长

输出力矩与法向力产生的力矩相平衡，可得：

令：f（φj）=（Δαnljcosβ-Δδjn）3/2

将上式在φj=π/4处泰勒展开，得：

将式（10）代入式（9），可解得Δαn，将式 Δαn代入式（7）得前半周期法向力具体表达式。

法向力变化率定义如下：ηfn=（Njn-Nj（n-1））/Nj（n-1）

磨损率变化率定义如下：ηmn=（δjn-δj（n-1））/δj（n-1）

步长不同得到的磨损率变化率不同，随着步长的增加变化率变大。因此在精度达到计算要求的情况下，步数应取较大值，以减少计算量，取步长λ=300转。

5 磨损补偿平衡分析

两啮合点处尺寸参数相同，则在计算过程中，假设滑动速度平均分配。啮合点产生的磨损量与机构尺寸相比较小，则在迭代过程中，认为速度不发生改变。

法向力在每一次磨损之后均发生变化，多次磨损之后法向力变化率趋近零，如图3所示，曲线关于φj=π对称。循环过程中变化率始终为零的点对应转角为φj=1.382rad、φj=2.892rad、φj=3.391rad、φj=4.902rad，在区间（1.382，2.892］∪（3.391，4.902］内，法向力变化率ηjn为正值，随着循环次数的增加各点变化率不断减小，经过多次循环之后趋近于零；在区间（0，1.382］∪（2.892，3.391］∪（4.902，2π］内，法向力变化率 ηfj为负值，随着循环次数的增加各点变化率不断增大，经过多次循环之后趋近于0。

图3 法向力变化率变化图Fig.3 Variation of Normal Force

磨损率变化率随循环次数的变化，如图4所示。由图可知，磨损率变化率的变化规律与法向力变化率的变化规律相似。在循环计算过程中，变化率始终无变化的点为（1.382，0）、（2.892，0）、（3.391，0）、（4.902，0）。在区间（1.382，2.892］∪（3.391，4.902］内，ηjn为正值，经过多次循环之后趋近于零；在区间（0，1.382］∪（2.892，3.391］∪（4.902，2π］内，ηfj为负值，经过多次循环之后趋近于0。

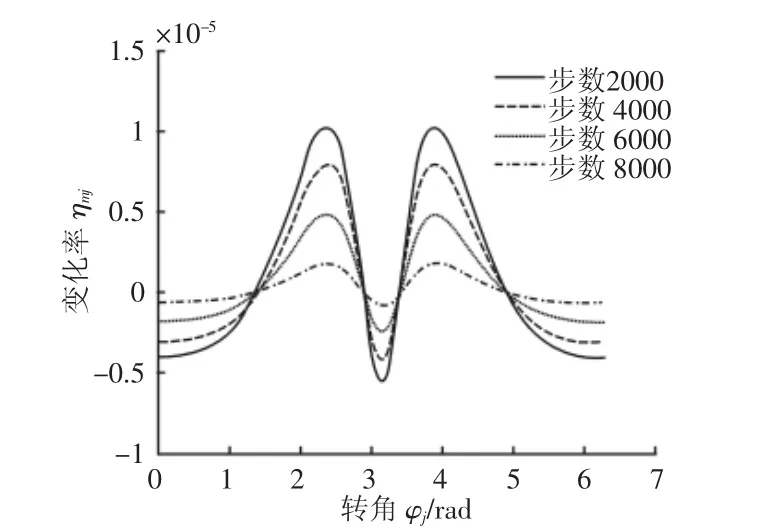
图4 磨损率变化率变化规律Fig.4 Variation Rate of Wear Rate

磨损率在一个步长内接触点参与接触的时间乘积为恰为钢球系转过Δαn各钢球中心产生的法向移动量δjxy，此时已经达到了一个平衡状态，将该状态称为磨损补偿平衡。所谓磨损补偿平衡就是在一定轴向力作用下，在一个步长内各接触点产生的磨损量与钢球系转角增加量经多次循环迭代之后均达到定值，且该磨损量与钢球系转角增加而产生的钢球中心移动量δj相等。在该平衡状态下各啮合点不会因为滑动速度大、名义压力大而产生足够的磨损量使该处产生间隙，即各啮合点不间断参与啮合。输入轴每旋转一次，啮合点法向载荷重新分配。在一啮合区处，滑动速度大、名义压力大，则磨损率大，磨损越严重。在运转过程中该处名义压力减小，磨损率有所下降。滑动速度小、名义压力小的啮合区在啮合点法向载荷重新分配后，法向作用力增加，磨损率必然增加。啮合副再磨损，法向力再分配，最终达到平衡状态，该状态下各啮合区磨损率不再发生变化。此时输出轴在恒定的轴向力作用下，减小行星盘与输出轴之间的距离，补偿啮合点产生的磨损，实现等速传动机构的实时无隙精密传动。

6 结论

在运动过程中不存在两啮合点均为纯滚动的情况，根据滑移理论认为两啮合点出的滑动速度相等。在初始磨损阶段，一周期内的磨损率变化率只存在四个为零的固定点，在部分区间内大于零，在部分区间内小于零。啮合点经过较多次磨损之后，磨损率变化率趋近于零，磨损率趋向于一稳定值，等速传动机构进入稳定磨损阶段。在稳定磨损阶段之后的每一次磨损中，由于转角Δα增加而产生的各点法向移动量与各点产生的磨损量相等，达到一种动态的磨损补偿平衡状态。该状态下每一迭代产生的磨损量可由转角增加量产生的法向移动量补偿，实现等速输出机构的实时无隙精密传动。