拮抗变刚度关节驱动器设计与特性分析

周建军，李 静，胡 涛，尚辉辉

（杭州电子科技大学 机械电子工程研究所，浙江 杭州 310018）

1 引言

关节驱动器是机器人的核心组成部分[1]，其设计的好坏直接决定机器人的整体表现。由于传统机器人在功率质量比、力质量比、柔顺性等方面与人存在很大的差距，以至于在运动性、安全性、能量利用率上无法达到要求；为了从根本上增强人机交互的安全性和对环境的适应性，柔顺关节驱动器逐渐成为研究的热点。

驱动器的柔顺性根据实现方法可分为主动柔顺和被动柔顺：（1）主动柔顺是指通过软件程序定义驱动器的柔性，使驱动器表现出具有类似于理想弹性元件的行为特性；（2）被动柔顺是指在传统刚性驱动器中引入弹性元件或弹性机构（如扭簧等），使该驱动器具备了类似于弹性元件的固有柔性特性[2]。

国内外已有很多关于驱动器方面的研究。在1995年，文献[3]提出SEA（SeriesElasticActuators）的概念，如今发展到VSA（Variable Stiffness Actuators）[4]，即变刚度驱动器。变刚度驱动器通过将简单的弹性元件或复杂的弹性机构与传统的驱动器组合，实现预先设计的变刚度特性。其优点在于使得驱动器具备了柔性的特点，增强驱动器的安全性，减弱外界冲击，内置弹性元件使系统具有储能和释放能量的特点；但弹性元件的引入增加了系统的复杂性，对系统控制和稳定性提出了更高的要求。国外已有一批代表性的成果，根据不同的刚度调节原理将所设计的成果概括为四类：（1）平衡位置控制变刚度[5-6]；（2）仿生拮抗作用变刚度[7]；（3）有效弹性物理结构变刚度[8]；（4）弹性结构预调整控制刚度[9]。尽管国内变刚度驱动器的研究起步较晚，但也有不少成果，如可变刚度柔性关节和多指灵巧手等。在前人研究基础上，设计一种仿生拮抗变刚度关节驱动器，该驱动器由双驱动电机、弹性元件及带轮等零件组成，可以得到良好的刚度变化特性，适用于不同载荷应用环境，具有一定的储能能力。

2 拮抗变刚度驱动器结构设计

2.1 拮抗驱动原理

拮抗驱动最典型的例子就是肘关节的肱二头肌和肱三头肌。肱二头肌和肱三头肌是一对既拮抗又协调的屈肌和伸肌，一方收缩，另一方放松，或一方放松，另一方收缩，通过两者相互之间的收缩与放松，实现肘关节的屈伸运动。对现有仿生拮抗柔顺驱动器分析可知，拮抗驱动的主要实现形式是人工气动肌肉拮抗驱动、液压伺服拮抗驱动和电机弹簧拮抗驱动。由于气动肌肉驱动和伺服驱动本身的粘弹特性，控制问题很难实现，综合考虑，采用电机弹簧拮抗驱动。

2.2 变刚度原理

变刚度机构是仿生关节的关键组成部分，是区别于传统刚性驱动器的重要部件，能够直接影响关节的变刚度性能。由于弹性元件的引入，变刚度机构应该具有非线性特性。以弹簧为例，其中，xOA和xOB分别代表左右弹簧变形后的长度，x代表弹簧初始长度。

假设1：两个弹簧为线性弹簧，具有相同的弹性系数k，且分别由两个电机独立控制，这时中心块受到的合力为：

根据刚度定义，该驱动模型输出刚度K：

由上式可知，系统的刚度为一个常数，与弹簧的形变量无关。因此，此种机构无法实现刚度可调。

假设2：弹簧为非线性（弹簧的刚度K随弹簧形变量的变化而变化），假如k（x）具有抛物线特性，中心块的受力如下：

根据刚度定义：

上式表明，系统的刚度与弹簧的形变量有关且呈线性关系。

由上述假设可知，机构具有变刚度特性的必要条件是驱动器中的弹性元件为非线性。

本结构用弹性张紧装置替换传统带传动中的高刚性的张紧装置[10]，而同步带在弹性张紧轮作用下受力张紧，同时，同步带将压迫弹性张紧装置产生变形，利用张紧装置变形过程中表现出来的非线性特点，进行拮抗变刚度驱动器的设计。

2.3 拮抗变刚度关节驱动器结构设计

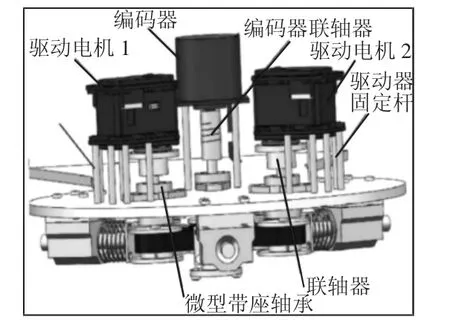
图1 变刚度驱动器模型Fig.1 Model of Variable Stiffness Actuator

一般的拮抗驱动，其单向张紧的特点使得关节活动范围受弹簧有效长度的限制，且其驱动力矩受限于单个动力源的最大驱动力矩。为了克服单向拮抗驱动的局限性，在相互拮抗的动力源之间引入第三个弹性元件，实现循环转动。基于以上原理，设计了三维模型，如图1所示。该驱动器模型包括舵机，同步带轮，同步带，联轴器，轴承座，线性弹簧，张紧装置，连杆及连接件。其中，两个舵机固定于机架背部，并通过联轴器分别连接带轮1、2，再通过同步带实现三个同步带轮之间力和运动的传递，连杆与带轮3连接；张紧装置由三个间隔120°的张紧轮构成，并通过轴承座约束，分别用相同的线性弹簧提供张紧力。

3 数学模型建立与静态刚度特性分析

经过设计计算，同步带轮分度圆直径d=26.7mm，同步带长=363mm以及张紧弹簧的自由长度H0=35.62mm。根据这些参数，对拮抗变刚度驱动器进行准确的数学建模，并以此模型对驱动器进行静态刚度特性分析，并为后面的动态性能仿真提供模型基础。

3.1 数学模型

刚度即单位形变量所需要的力或力矩，刚度特性则定义为驱动器输出力矩T与转角θ3之间的关系，即K=∂T/∂θ3。带轮a、b分别代表驱动轮和输出带轮，且关于张紧轮移动副轴心线对称分布，同步带受张紧轮的作用力F发生内凹，此时同步带与垂直线形成锐角α，为了方便数学模型的建立，对张紧轮半径r做了近似处理：r≈0，且忽略同步带实际传动过程中，带齿与轮齿啮合间出现的滑齿。

各几何尺寸的含义分别是：初始夹角α0、轮间同步带初始长度l0、带轮半径R、带轮中心距ɑ0，如图2所示。

图2 驱动器结构示意图Fig.2 Diagram of Actuator’s Structure

轮a对轮b的力矩Tab为：

式中：k—张紧弹簧的弹性系数；R—同步带轮的半径，且三个带轮一致；hab—t时刻对应的弹簧形变量；c0、c1—张紧轮和同步带的接触点在初始时刻和t时刻与带轮圆心连线的距离；l0、l—初始时刻和t时两带轮之间同步带的长度。驱动器的扭矩T为：

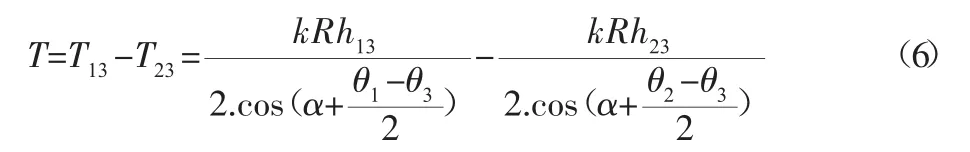
根据刚度定义，扭矩T对输出转角θ3求导即为刚度，即：

3.2 驱动器静载刚度特性分析

驱动器关节静载下的刚度特性是指当关节上加载缓慢匀速的角位移时，驱动器所表现出来的刚度变化规律；t时刻的驱动器的静态刚度可简单的理解为驱动器空载刚度的基础上，在外部静载的作用下引起的刚度变化，此时的刚度由驱动轮运动规律（θ1，θ2）和负载运动规律θ3两部分决定的。

在图示所示2几何中，根据它们之间存在的几何关系计算化简之后可得=363mm，R=13．35mm，a0=78mm，解得 α0=59．62°，l0=99．79mm。

将上述参数代入式（7）中，可以得到该驱动器刚度特性的数学模型，然后在MATLAB中进行静态刚度特性分析，其曲线，如图3所示。

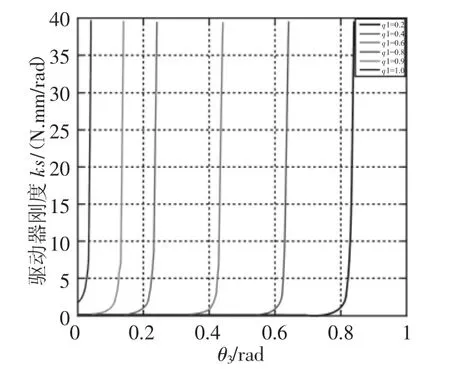
图3 静态刚度特性图Fig．3 Static Stiffness Characteristic Diagram

在不同空载刚度下，受到静载作用时所表现出来的刚度变化规律一致。通过对比发现，随着δ值的增大，驱动器的最小刚度随之增大，且预留给θ3的角位移量变小，即回驱角区间将减小，乃至于消失（当 δ=1．0°时）。以 δ=0．2°为例，当 θ3≤0．7rad 时，随 θ3的增大，驱动器的刚度变化并不明显，说明当驱动器受到撞击时，在该区间内驱动器有一个较大的回驱角度，可有效的保证驱动器和使用者的安全；当θ3＞0．7rad时，驱动器的刚度特性近似于指数型变化规律，在该区间里，驱动器在快速达到较高的刚度，近似刚性的状态。

随着空载关节初始刚度的增加，即图3中从右向左δ的增加，驱动器的回驱角区间将减小，乃至于消失（当δ=1．0°时）。一个合适的回驱角区间对驱动器的安全性和动态性能影响较大。

4 驱动器动力学分析

4.1 动力学模型

对系统进行动力学分析，系统的动力学方程如下：

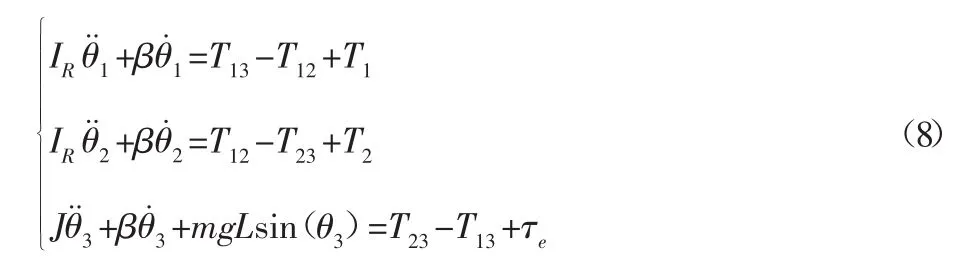
式中：IR—驱动轴上的转动惯量；J—输出端转动惯量；β—驱动轴上的等效阻尼；m，L—输出杆的质量和长度；θ1、θ2、θ3—三个带轮的角位移；T12、T13、T23—同步带对带轮的扭矩，且规定逆时针方向为正方向；T1、T2—电机的控制扭矩；τe—外部负载扭矩。

系统的拉格朗日方程，动能及势能如下所示：

系统除了受有势力作用之外，同时还受到非有势力M1，M2的作用，系统是两自由度机械系统，通过拉格朗日方程建立该系统的运动微分方程，表达式如下：

4.2 动力学仿真与实验验证

在ADAMS中，建立驱动器模型并搭建小球撞击实验平台，为了更好的反映驱动器在蓄能方面的能力，取转角差δ=0°和转角差δ=15°进行小球与驱动器连杆碰撞实验模拟，观察碰撞之后小球的平抛运动；虚拟样机实验平台得到，如图4所示。

图4 驱动器虚拟样机模型Fig．4 Model of Actuator Virtual Prototype

通过观察小球落在地面上的距离可知，柔性状态下小球平抛得更远，这得益于连杆与小球碰撞接触时能量的传递；连杆获得的能量以弹性势能的方式储存在弹簧中，柔性状态下良好的储能特性使得小球在平抛运动中的水平位移增加；而且撞击过程中都有一定的回驱现象，实验说明该驱动器在发生撞击时具有一定的安全性。

为了验证仿真结果的可靠性，制作实验样机并搭建实验平台，进行小球撞击实验。该实验室为对比实验，连杆从同一角度，在不同的刚度条件下，以相同的速度变化规律摆动撞击小球。

图5 小球撞击实验Fig．5 Test of Ball Impact

撞击实验结果，如图5所示。转角差δ=0°对应于2cm的水平位移，而转角差δ=15°对应于8cm的水平位移。产生该现象的主要原因是在撞击时，刚度不同且两次撞击发生了回驱现象。由于弹性元件的储能，小球平抛得更远，且初始刚度是δ=0°时，回驱角度大，传递给小球的动能小；通过该实验说明驱动器在发生撞击时，具有一定的储能性和安全性。

5 结论

根据变刚度驱动器的系统组成，以及生物体关节拮抗驱动原理，设计了一种两自由度变刚度关节驱动器；通过对驱动器数学模型的推导演算，得到了该驱动器刚度变化特性，分析了刚度变化与转角的关系，说明该驱动器具有变刚度特性和储能特性；通过对比实验，初步验证了驱动器良好的储能特性和安全性，实验结果与理论模型基本一致。最后，研制了一台拮抗变刚度驱动器样机，用该驱动器进行简单的小球撞击实验，初步验证了驱动器良好的储能特性和安全性。