核极化的特征选择算法在LSSVM中的应用

王建国，陈肖洁，张文兴

（内蒙古科技大学 机械工程学院，内蒙古 包头 014010）

1 引言

在支持向量机（support vector machine，SVM）中，关于 SVM的核函数选择，高斯核备受青睐。究其原因为高斯核具有稳定优越的性能，可以使SVM获得较好的推广性[1-2]。高斯核的宽度参数决定了样本数据分布的复杂程度，进而，影响特征空间中最优分类超平面的泛化性能，高斯核的形式：

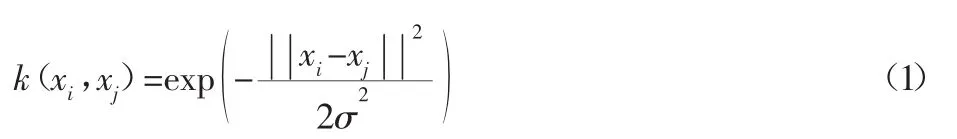
为了体现样本中不同特征的重要性程度，即区别各个特征对分类贡献率的差异，引入了多宽度（多参数）高斯核[3]，假设x有D个特征量，xi［m］，xj［m］是其中的第m个特征量，其形式如下：

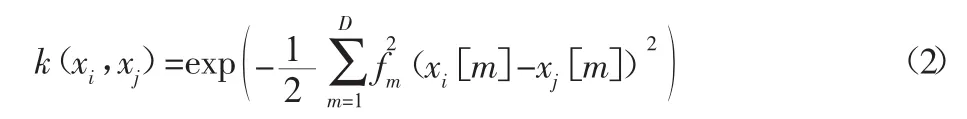
显然，我们可以利用fm值的大小来衡量不同特征的重要性差异，将其应用到特征选择中。特征选择一般是指按照某种评估标准从输入特征集中选择出最优的特征子集，去除冗余、无关特征以达到提高学习精度的目的。现在，关键问题是，fm值的确定问题。高斯核的核参数优化方法主要有：（1）不断循环SVM分类器迭代优化算法[4]和粒子群优化寻优算法[2]，该两种方法的缺点为计算量大；（2）独立于分类器SVM的核度量标准[5]的方法，如最大化核极化的算法[6-8]，不足之处是以SVM为分类器，求解凸二次规划问题来取的最优解。因此，我们采用优化独立于分类算法的核度量标准—核极化来优化多参数高斯核中的多参数，并以最小二乘支持向量机（leastsquaressupportvectormachine，LSSVM）为学习器，求解一组线性方程组来得到方程的最优值，简化计算量，提高计算效率。

2 最小二乘支持向量机（LSSVM）

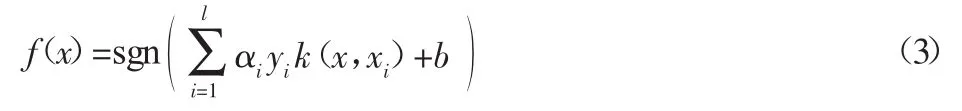
式中：k（xi，xj）—核函数；b—偏置量；αi≠0 的训练样本为支持向量，这里αi，∀i通过求解下面的线性方程获得：

式中：矩阵 Ω=yiyjφT（xi）φ（xj）=yiyjk（xi，xj），i，j=1，L，l；YT=［y1，L，yl］；I—单位矩阵，与 Ω 同阶；I1=［1，L，1］T；α=［α1，L，αl］T。

式（4）的约束优化问题是[9]：

式中：γ—规则化因子；ei—误差变量；φ（xi）—非线性映射，将样本集从输入空间映射到高维特征空间。构建Lagrange方程，并对原始优化参数求偏导，整理，可得式（4）[10]。

针对多分类问题时，目前主要采用多目标优化和组合编码2种方法[4]。一次性求解所有分类参数的多目标优化方法，因其求解变量数目较大，求解过程复杂，在实际应用中，并不适用。因此，我们主要讨论组合编码方法中的一对一编码，构造多个二分类LSSVM来实现多分类分类。

3 核极化及其特征选择算法

2005年，文献[5]借用物理学概念，提出了核极化度量标准（kernel polarization，KP），即：

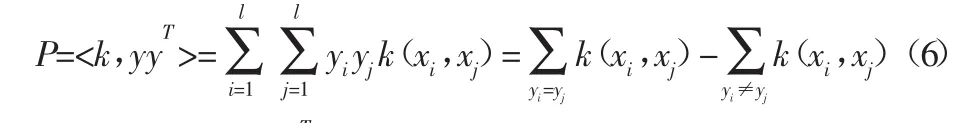
式中：k—核矩阵；yyT—理想核矩阵；＜·，·＞F—矩阵之间的Frobenius内积。

由式（6）可知：当同类样本点靠近（k（xi，xj）取较大值），异类样本点远离（k（xi，xj）取较小值）时，可以使核极化值P较大。由此可知，最优核参数fm可以通过最大化P得到，若某一特征x［im］越重要，则fm值越大，对应的Pm值越大。具体的特征选择算法步骤如下：

步骤 1：初始化 f=diag（1，L，1）；

式中：0．05—学习因子，迭代停止条件为fm的相邻两次的函数值之差的绝对值小于10-5；

步骤3：转步骤2，直至满足停机条件；

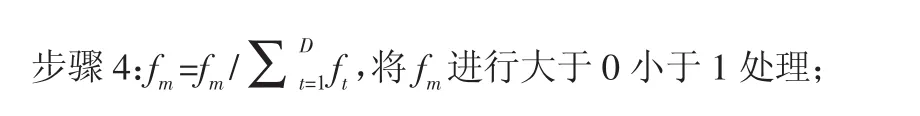
步骤5：排序fm，并记录其从大到小的先后顺序ftoped；

步骤6：按ftoped的顺序，依次增添样本中的一个特征量（即选取第一个，前两个，…，所有特征）到LSSVM分类器，进行LSSVM的训练和测试。

我们将核极化优化多参数高斯核的算法和特征选择联合起来考虑，利用核极化独立于学习算法的优势来，测定不同特征对分类的重要性贡献，和进行样本的特征选择，并用LSSVM分类器验证核极化的特征选择算法的正确性。所提算法的流程图，如图1所示。

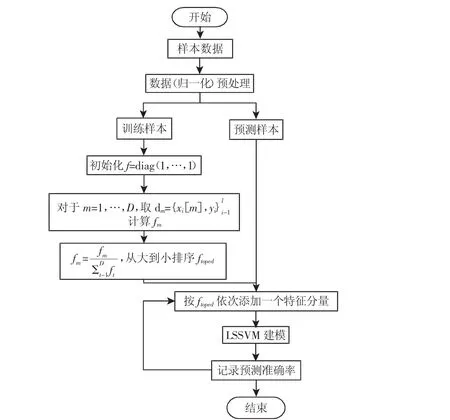
图1 算法流程图Fig．1 The Flow Chat of the Algorithm

4 实验部分

实验以LSSVM为载体来验证核极化优化多参数高斯核的特征选择算法的有效性。实验环境为Window7 32位系统，E-450 CPU，2GB RAM以及Matlab 2011a。从UCI机器学习数据库中选取5个数据集，基本属性如表1所示。

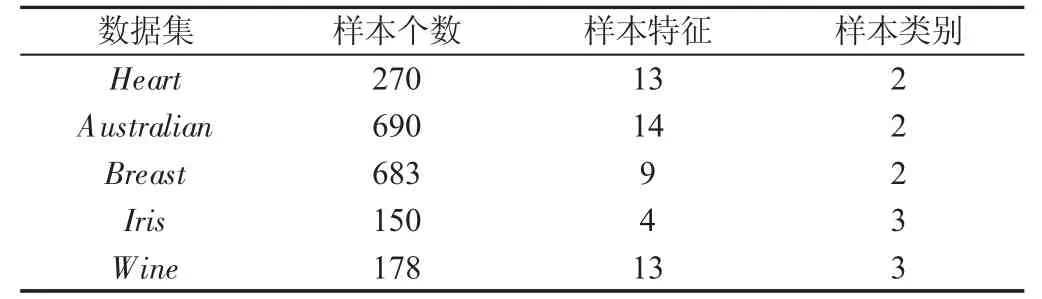
表1 实验数据集Tab.1 The Datasets of Experiments

Heart为二分类数据集，Heart包含270个样本，一个样本含有13个特征分量，具体特征属性为：年纪、性别、胸部疼痛类型、静息血压、血清类固醇、空腹血糖、静息心电图结果、最大心率、运动诱发的心绞痛、相对静止运动引起的抑郁症、峰值运动时的斜率、主要的血管数和患者类型。

Australian的数据集全称为Australian Credit Approval，二分类，包含690×14个样本。

Wisconsin Breast Cancer Database简称为Breast，二分类：良性（Benign）和恶性（Malignant）。该数据原有699个样本，因16个样本数据缺失，故实验中采用的样本个数为683个。实验时，采用的9个输入样本特征分别为肿块密度、细胞大小的均匀性、细胞形状的均匀性、边缘粘连性、单上皮细胞的大小、裸核、温和的染色质、正常核和有丝分裂等。

Iris是Iris Plants Database的简称，数据集为150×4，即包含150个样本，每个样本含有4个属性特征，如萼片和花瓣的长度等。Iris的类别为setosa、versicolor、virginica 3类，每个类别有50个样本。

Wine为经常使用的多分类数据集，全称为Wine Recognition Data，数据来源是对意大利同一地区不同品种的三种酒的大量研究、分析。Wine数据集的数据完整，没有空缺值，大小为178×13，三分类，178个样本，每个样本具有13个输入特征，即酒精、羟基丁二酸、灰烬、灰分碱度、镁、总酚、黄酮类化合物、非黄酮类物质酚类、花青素苷、彩色亮度、色调、提取稀释的葡萄酒物质和脯氨酸。在数据文本“wine.data”中，178行，行代表酒的样本，其中，第1类：59个样本，第2类：71个样本，第3类：48个样本，即共有178个样本；14列，第一列：类标志属性，标记为“1”，“2”，“3”等三类；第2列到第14列为样本输入特征的样本值。

4.1 实验

实验（a）：对于每一个数据集，选取样本的为训练集，剩余样本的作为测试集。实验中，首先，利用第3部分介绍的核极化的特征选择算法，排列出各个特征的先后顺序和记录其相应的fm值；然后，设置分类器LSSVM的参数为：高斯核σ=1，γ=0.06；最后，对于每添加一个特征，进行LSSVM训练和预测，记录相应的预测准确率。实验结果，如图2所示。通过条形图显示了Heart数据集各个特征的重要性程度，如图3所示。

实验（b）：在数据集的所有特征上，进行SVM和LSSVM的训练和预测，训练集和测试集的设置，如图2（a）所示。分类器的参数为：高斯核，σ=1，C=100，γ=0.06，进行 10 次的独立实验，表 2记录了10次实验运行时间的平均值（单位为s），表3记录了10次实验分类准确率的平均值和标准差，表2和表3中的粗体数值为该设置参数下最好的实验结果值。表4给出实验（b）的统计检验结果（在Excel 2007分析工具库中，首先，利用“F-检验：双样本方差”判断两样本的总体方差是否相同；然后，若两总体方差齐，则进行“t-检验：双样本等方差假设”，否则，进行“t-检验：双样本异方差假设”）。

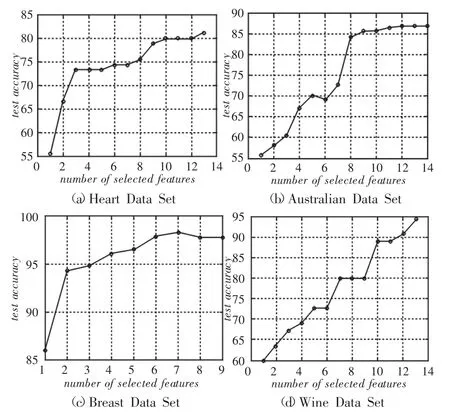
图2 算法实验结果图Fig.2 Experimental Results of the Algorithm

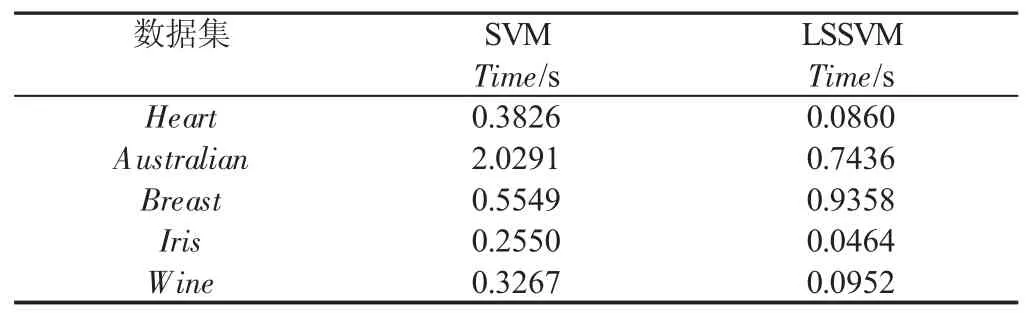
表2 LSSVM和SVM运行时间的实验结果Tab.2 The Running Time of LSSVM and SVM

表3 LSSVM和SVM分类准确率的实验结果Tab.3 The Accuracy of LSSVM and SVM

图3 Heart数据集不同特征的重要性程度Fig.3 The Importance of Different Features on Heart Dataset

4.2 实验分析

实验（a）：对于表1的每个数据集，遵循样本特征重要性大小的先后的原则，图2显示，LSSVM对于每添加一个特征的实验准确率均有或大或小的提高。具体而言，重要性程度大的特征对分类贡献较大，原因是图像由开始的比较陡峭渐变为后来的平稳（如Heart、Australian和Breast数据集）。图3的条形图说明数据集的各个特征对分类的贡献大小是有差异的。实验（a）的结果表明，采用核极化的特征选择方法是有效的。在实际应用中，我们完全可以采用对分类贡献率比较大的样本特征来预测样本，节省运算时间，提高预测效率。

实验（b）：表2的数据表明，在4个数据集的运行时间上，LSSVM明显都优于SVM；在分类准确率上，如表3数据所示，采用LSSVM所达到的实验结果在3个数据集上都优于SVM，在Iris和Wine上，2种方法的实验结果基本相当。为了确保实验结果的客观性，我们对分类准确率和运行时间进行了显著性水平为0．05的t假设统计检验，统计结果记录在表4中。就分类准确率而言，表4的统计结果显示，LSSVM在3个数据集上显著性差异地优于SVM，且在Wine上相对于SVM没有显著性差异；仅在Iris上劣于SVM，但根据表3的Iris的分类准确率95．8824（SVM）和94．3137（LSSVM）可知，2种方法所得结果差异很小。表4的统计结果同样说明，使用LSSVM相比SVM能明显地提高计算效率。从实验（b）的结果可以判断，LSSVM作为特征选择的分类器是高效的。

表4 数据集上的实验结果的t假设检验结果Tab.4 The t Hypothesis Testing of Datasets Experiments

5 结论

为了解决LSSVM的特征选择问题，提出了核极化的特征选择算法，并将选择出的特征应用于LSSVM。UCI数据集上的实验结果表明，所提的特征选择算法的有效性和LSSVM分类器计算的高效性。