三鞍座卧式容器鞍座许用沉降量研究

周博为，谢利来，贺小华

（南京工业大学 机械与动力工程学院，江苏 南京 211816）

1 引言

随着容器的大型化，三鞍座及多鞍座卧式容器应用逐渐增加。现行多鞍座卧式容器没有统一的设计标准，大多采用三弯矩理论计算弯矩和鞍座反力，再应用双鞍座卧式容器的Zick校核方法对应力进行校核[1]；欧洲协调标准EN13445《非直接受火压力容器》[2]提出了一种多鞍座卧式容器的设计方法。研究表明，采用多鞍座支撑能够有效改善超长型容器筒体跨中截面处的应力，且抑制容器的振动[3-4]。工程应用中，由于地基的不均匀沉降导致任意相邻两个鞍座间存在垂直位置偏差，使鞍座支反力与筒体中的弯矩发生变化，从而使得筒体中的附加应力增大，给容器的安全运行带来不利的影响[3，5]。文献[1-2]两种方法中鞍座反力的计算都没有考虑基础不均匀沉降的影响。由于基础沉降的诸多不确定性，一些设计者倾向于在采用三弯矩方程计算各个鞍座轴向弯矩和支反力的基础上引入（1．2～1．4）的安全系数[6]，但此种做法缺乏理论依据。文献[7]对含沉降三鞍座结构进行理论计算，指出当中间鞍座沉降量大于同等结构双鞍座跨中截面自由变形量时，设置三鞍座会显著增大筒体跨中截面的轴向弯矩，此时不宜设置三鞍座。文献[8]通过对多鞍座结构进行理论分析，提出了一种简单方法用来计算鞍座正负沉降对轴向弯矩、支反力的影响；文献[3]通过对含沉降三鞍座结构进行了理论和有限元数值模拟，指出了“有沉降的三弯矩方程”理论解的正确性，并且指出理论计算解要比有限元解保守，如果按介于简支和固支之间的约束进行计算可以得到较好的修正结果。需要指出的是，上述文献大多针对含沉降的多鞍座结构进行了轴向弯矩和支反力的计算，没有考虑正负向不同沉降对筒体应力的影响。

针对含沉降的三鞍座卧式容器进行研究，对比分析了由标准NB/T 47042-2014[9]和由临界轴向弯矩得出的临界沉降量对筒体应力的影响，给出了三鞍座卧式容器的合理许用沉降量，为含沉降三鞍座卧式容器设计提供借鉴。

2 模型与方法

文献[6]指出，长径比L/D＞10（L—两封头切线间距离；D—容器内直径）的卧式容器多采用多鞍座支撑，文献[10]研究表明，双鞍座/三鞍座临界长径比L/D≥（10～12）。文献[5]的研究表明，三鞍座卧式容器适宜的鞍座位置为A=0．145L（A为鞍座中心距封头切线处的距离）。以V=270m3卧式容器为分析对象，筒体长径比为L/D=10、12、15、20，鞍座位置设为 A=0．15L，分析工况为满水工况，具体参数，如表1所示。

表1 不同长径比分析模型的结构参数Tab.1 The Structure Parameter of Different Analysis Model

根据容器结构对称性，计算中选取1/2模型，采用20节点solide95单元的六面体网格。计算边界条件为：对称面施加对称约束，左鞍座底部施加固定约束，右鞍座底部施加x与y方向的位移，中间鞍座底部在y方向上施加沉降量，建立的有限元几何模型，如图1所示。中间鞍座含沉降量δB。分析中载荷为：容器自重及沿高度线性变化的静水压强。

图1 有限元分析模型Fig．1 FEA Model

3 不均匀沉降的理论分析

对称布置三鞍座卧式容器的力学模型是一次静不定结构，文献[11]指出三鞍座的不均匀沉降可简化成如图2（中间鞍座沉降δB）和如图3（边鞍座沉降δC）的两种情况来考虑。文献[12]对三鞍座沉降进行分析指出，对于边支座发生了相对沉降，可以假设左右支座仍处在同一个水平面上，从而将边支座处的相对沉降折算到中间鞍座处。后续分析中只考虑中间鞍座处的沉降对筒体应力的影响（假设向上为正，向下为负）。

图2 中间鞍座沉降简化力学模型Fig．2 Mechanical Model with Settlement δBof Middle Saddle

图3 边鞍座沉降简化力学模型Fig．3 Mechanical Model with Settlement δCof Side Saddle

3.1 标准许用沉降量［e1］

依据NB/T 47042-2014中的规定，在对称布置的三鞍座容器中应限制地基不平度以及两相邻鞍座在安装时存在的垂直误差或非均匀沉降，以避免由此产生的附加鞍座反力以及附加弯矩。两相邻鞍座的允许垂直偏移量可由下式计算得到：

式中：l—两鞍座间的跨度；t—筒体壁厚；c—轴向弯矩变化系数，其值可取（0．2～0．5）；当取 c=0．5 时，分析模型鞍座的许用沉降量 e1[]，如表2所示。

表2 分析模型鞍座的许用沉降量［e1］Tab.2 The Allowance Settlement［e1］of Saddle for Analysis Model

3.2 由轴向弯矩确定的临界许用沉降量［e2］

在双鞍座容器中，筒体跨中截面的轴向弯矩是限制筒体长径比增大的主要原因，设置三鞍座能有效减小筒体跨中截面的轴向弯矩，然而若当三鞍座容器中鞍座沉降所产生的附加弯矩超过双鞍座筒体跨中截面处的弯矩M1时，设置三鞍座就毫无意义。此时的沉降量也可定义为中间鞍座的临界许用沉降量。

由文献[9]可知双鞍座跨中截面处的弯矩M1为：

式中：F—支反力；R—筒体半径；H—封头曲面深度。

文献[11]指出，无沉降时，在边鞍座、中间鞍座截面处的轴向弯矩分别为：

当中间鞍座发生沉降时，在中间鞍座截面处的轴向弯矩为：

式中：I—极惯性矩，I=πR3t。将式（4）代入式（5）可得：

当中间鞍座处发生向上沉降时，令MδB=-M1，由式（6）可得：

分析模型鞍座的临界许用沉降量［e2］，如表3所示。对比表3与表2可知，标准NB/T 47042-2014中给出的许用鞍座沉降量［e1］要远小于依据3．2节给出的临界鞍座许用沉降量［e2］。

表3 分析模型鞍座的许用沉降量［e2］Tab.3 The Allowance Settlement［e2］of Saddle for Analysis Model

4 计算结果与分析

4.1 沉降量对筒体应力的影响

确定了分析模型鞍座的许用沉降量范围，如表2、表3所示。后续有限元分析模型中鞍座沉降量δB选取（-40～40）mm范围。不同长径比分析模型筒体与支座连接处最大Tresca当量应力与一次局部薄膜应力随沉降量δB变化的关系图，如图4所示。由图4可知，筒体的各种应力与沉降量δB基本上呈线性变化，相同沉降量下，长径比L/D越大，当量应力值越低。正向沉降对于筒体应力的影响要大于负向沉降的影响，这表明相对于负向沉降要严格控制鞍座的正向沉降。

表4 分析模型鞍座的沉降量δBTab.4 The Settlement δBof Saddle for Analysis Model

图4 筒体与鞍座连接处最大应力随鞍座沉降量δB的变化Fig．4 The Changes of Maximal Stresses at the Connection between Shell and Saddle Along with Settlement δBof Saddle

为了分析许用沉降量 e1[]、e2[]对于筒体应力的影响，分别求出不同长径比下鞍座在沉降量为 e1[]、e2[]时筒体中各应力与未发生沉降时筒体中各应力的相对变化率Δ%，结果如表5～表8所示。

表5 鞍座沉降量为 e1[]、e2[]时筒体与鞍座连接处最大应力的相对变化率（L/D=10）Tab.5 The Relative Variation Rate of the Maximal Stresses at the Connection Between Shell and Saddle When the Settlements of Saddle aree1[]ande2[]（L/D=10）

表6 鞍座沉降量为 e1[]、e2[]时筒体与鞍座连接处最大应力的相对变化率（L/D=12）Tab.6 The Relative Variation Rate of the Maximal Stresses at the Connection Between Shell and Saddle When the Settlements of Saddle aree1[]ande2[]（L/D=12）

表7 鞍座沉降量为 e1[]、e2[]时筒体与鞍座连接处最大应力的相对变化率（L/D=15）Tab.7 The Relative Variation Rate of the Maximal Stresses at the Connection Between Shell and Saddle When the Settlements of Saddle are e1[]and e2[]（L/D=15）

表8 鞍座沉降量为 e1[]、e2[]时筒体与鞍座连接处最大应力的相对变化率（L/D=20）Tab.8 The Relative Variation Rate of the Maximal Stresses at the Connection between Shell and Saddle When the Settlements of Saddle are e1[]and e2[]（L/D=20）

由表5～表8可以得出：在鞍座许用沉降量 e1[]、 e2[]中，NB/T 47042-2014中给出的许用沉降量 e1[]对应力的影响明显小于 e2[]对应力的影响，且在各长径比分析模型中，正向沉降对应力影响的相对变化率明显大于负向沉降的相对变化率，含 e1[]沉降量分析模型中，正向沉降对于应力影响的最大相对变化率为24%，负向沉降对于应力影响的最大相对变化率的绝对值为13%；而含 e2[]沉降量分析模型中正向沉降对于应力影响的最大相对变化率为61%，负向沉降对于应力影响的最大相对变化率的绝对值也达到了47%。这表明正向沉降对于筒体中的应力影响更为显著，因此对于正向沉降量的限制要求要高于负向沉降的要求。采用这里3．2节中确定的临界沉降量 e2[]对筒体应力的影响过于显著，在工程实际中应按NB/T 47042-2014中给出的许用沉降量对沉降量加以控制。

4.2 合理的许用沉降量

由上一节的分析可知，鞍座沉降量对筒体应力影响显著，应按标准NB/T 47042-2014中规定值控制沉降量。由于正负沉降量对筒体应力存在不同的影响，而NB/T 47042-2014中未差异化地给出不同正负沉降量的控制要求。本节结合双鞍座与三鞍座容器的应力特点，提出了较符合实际的许用沉降量。

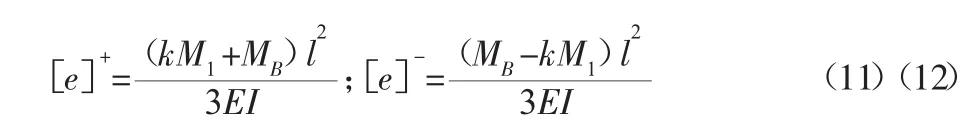
分析模型在不同值时的许用沉降量，如图5所示。当k=1．0时，许用沉降量即为临界许用沉降量 e2[]，由沉降量对筒体应力影响的分析可知，临界许用沉降量 e2[]相对于NB/T 47042-2014给出的许用沉降量 e1[]对于筒体中应力的影响过于显著，应对其加以限制。当k=0．5时，正向沉降上的许用沉降量与标准中的许用沉降量基本一致，负向沉降的许用沉降量绝对值大于标准中的许用沉降量。以下分析当k=0．5时许用沉降量［e］对筒体中应力影响的相对变化量Δ%。

图5 鞍座的许用沉降量［e］Fig．5 The Allowance Settlement［e］of Saddle

k=0．5时许用沉降量［e］对筒体中应力影响的相对变化量Δ%，如表9所示。与表5～表8相比较，在正向沉降上，［e］与 e1[]对筒体应力影响的相对变化量基本一致，含沉降［e］的分析模型应力最大变化量为28．3%；在负向沉降上，［e］对应力的相对变化量大于 e1[]对于应力的变化量，但均小于正向沉降的变化量，负向沉降［e］对应力的最大变化量为26．7%。

表9 鞍座沉降量为［e］时筒体与鞍座连接处最大应力的相对变化率（k=0.5）Tab.9 The Relative Variation Rate of the Maximal Stresses at the Connection Between Shell and Saddle When the Settlement of Saddle is［e］（k=0.5）

表 9［e］+、［e］-引起的应力变化率与表 5～表 8 中基于标准［e］引起的应力变化率，二者较为接近。因此由（0．2～0．5）得出的许用沉降量［e］可作为工程实际中三鞍座沉降量的控制值，当然其工程适用性仍有待进一步的实验验证。当k=0．5时，不同厚度分析模型推荐的许用沉降量［e］，如表10所示。与表2比较，正向沉降［e］+接近NB/T 47042-2014中规定的［e1］，而负向沉降［e］-绝对值则大于［e1］，正负沉降对于应力的影响均在28%左右。实际结构中，对于较大沉降量的多鞍座结构，必须考虑沉降量对筒体应力的影响。

表10 分析模型推荐的许用沉降量［e］Tab.10 The Recommend Allowance Settlement［e］of Saddle for Analysis Model

5 结论

对满水工况下，含不均匀沉降的三鞍座卧式容器分别进行了理论计算和有限元应力分析。通过理论计算给出了结合标准NB/T 47042-2014的许用沉降量 [e1]以及由轴向弯矩确定的临界许用沉降量 [e2]，结果表明，[e2]对筒体应力的影响过于显著，且明显大于[e1]的影响。三鞍座卧式容器中，正向沉降对于应力的影响比负向沉降对于应力的影响更为显著，因此相对于负向沉降量，要严格控制正向沉降量。另外，结合标准中的许用沉降量限制值，考虑正负沉降量对筒体应力影响的不一致性，提出了较为合理的许用沉降量计算的方法，即，k=0．5，依照其计算得到的许用沉降量对于筒体应力的影响相对较为合理，可为工程实际提供参考。