线性二次型在柔性机械臂抑振控制中的研究

郭珂甫，刘广瑞，王庆海

（郑州大学 机械工程学院，河南 郑州 450001）

1 引言

近些年来，随着工业技术的发展，以柔性机械臂为代表的刚柔耦合多体动力学系统得到迅速发展。柔性机械臂具有运作速度快、载重/自重比高以及工作容积大等诸多优点，在航空航天、车辆工程、现代制造等领域得到广泛应用。但在实际应用中，柔性连杆由于材料等因素引起的弹性振动问题，导致其不能完成准确的定位和预定的轨迹，是该研究领域的一个热点问题[1]。

柔性机械臂系统的研究内容主要由动力学建模理论和振动控制策略两部分组成。在动力学建模方法的研究中，文献[2-3]基于假设模态法和Kane方程建立柔性机械臂的动力学模型，并分析不同模态阶数下的动力学响应；文献[4]提出了基于全局模态法建立柔性机械臂的动力学模型，给出具体的计算过程；文献[5]基于有限元法分析在不同模态频率下角速度的变化，并通过实验与仿真对比验证；文献[6]提出基于ANSYS和ADAMS联合仿真方法分析不同结构参数下柔性机械臂的频率响应变化。对于抑振控制方法的研究，文献[7]提出了基于Lyapunov稳定性的模糊自适应控制与模态速度反馈控制相结合的方法，抑制柔性臂弯曲和扭转振动，达到了一定的预期效果；文献[8]提出采用模糊控制算法和PD控制相结合的抑振策略，对弹性振动进行理论研究和实验分析；文献[9]提出一种新的线性力反馈控制策略，实验结果证明能有效抑制末端弹性振动。有关动力学建模的研究，仍然没有形成一个定性的建模理论。各种不同的主动控制方法在抑振方面都取得一定的效果，但仍然有很多不足。例如自适应控制在外界参数发生较大变化时鲁棒性变差等缺陷。在抑振控制方面，还有很多实际工程问题有待解决。线性二次型最优控制具有很好的鲁棒性，计算简洁且易获得最优解，在结构主动控制中得到广泛应用。结合遗传算法高效的寻优能力，该方法在实际工程中容易实现，具有很强的实用性。

首先分析柔性连杆的弹性变形，并在此基础上采用lagrange方程，建立考虑阻尼作用的末端有集中质量的柔性臂动力学模型，依据弯曲梁固有振型正交性对其进行简化。确定二阶模态下的系统的状态变量后，推导出以驱动力矩为输入，端部弹性变形和转角为输出向量的状态空间表达式。设计柔性臂系统的线性二次型最优控制策略，用遗传算法对LQR控制中的加权矩阵进行参数优化并建立Simulink仿真模型。分析研究优化前后柔性机械臂末端位置弹性运动的稳定性。

2 柔性机械臂的动力学描述

2.1 柔性机械臂的弹性变形描述

首先建立单连杆柔性机械臂的结构示意图，如图1所示。柔性机械臂是一个弹性悬臂梁，一端固定在旋转电机轴上，另一端自由，末端具有集中质量块，在水平面内绕电机转轴做旋转运动。图中：坐标系XOY—惯性坐标系；坐标系xoy—固定在柔性机械臂上的浮动坐标系，并始终与柔性机械臂的轴线相切；θ（t）—柔性臂的角位移；u（t）—伺服电机驱动力矩；ml—柔性臂的末端集中质量；ω（x，t）—固定在柔性机械臂上的浮动坐标x在t时刻的横向弹性变形量；l—柔性机械臂连杆的长度；h—连杆横截面高度；b—横截面宽度。

图1 柔性机械臂结构示意图Fig.1 Structural Model of Flexible Manipulator

为简化推导及动力学建模，对单连杆柔性机械臂做如下小变形假设：（1）忽略柔性臂轴向弹性变形及剪切变形，仅研究其横向弹性变形；（2）柔性机械臂的连杆长远大于其横截面尺寸；（3）忽略柔性机械臂的重力和空气阻尼等因素。

点P（X，Y）为连杆上的任意一点，根据结构动力学中等截面均质梁的弯曲振动偏微分方程，P点横向弹性变形量ω（x，t）可表示为

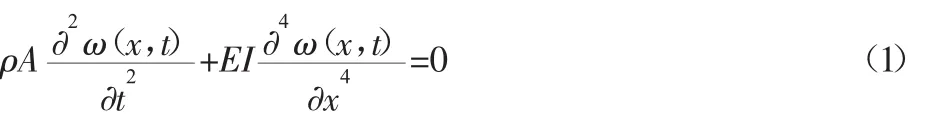
式中：ρ—柔性臂连杆材料的密度；E—材料的弹性模量；A—连杆的横截面积；I—连杆的截面惯性矩。

采用分离变量的方法求解此四阶常系数线性齐次微分方程，设

式中：W（x）—柔性机械臂在x处的横向振动幅值函数；q（t）—描

述运动规律的时间函数。将式（2）代入式（1），整理后有：

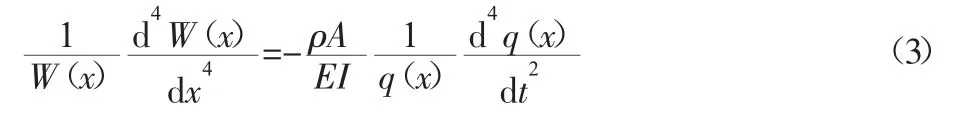
式（3）左右分别等于独立的常数，设这个常数为ω2，并定义β4=（ρA/EI）ω2，可分离出两个独立的常微分方程，求解就可以得到表示模态振型函数W（x）和时间函数q（t）。柔性机械臂作自由振动时弹性变形满足的微分方程边界条件可由如下表示：

在柔性机械臂与电机的固定端（x=0）处，横向振动位移为0，横向振动速度为0，即

在柔性机械臂的末端（x=l）处，弯矩为0和剪切力平衡分别满足：

通过上述边界条件，即可以得到柔性机械臂模态振型函数的表达式：

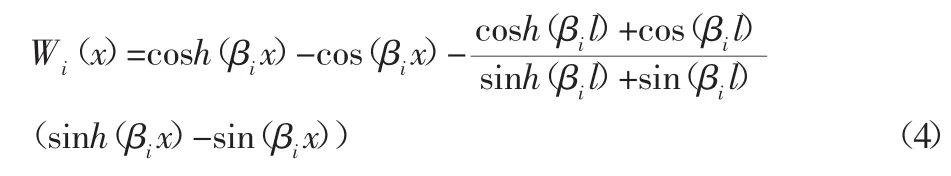
将ω（x，t）表示为与x有关的模态振型函数Wi（x）和仅与时间t有关的广义弹性坐标qi（x）的乘积求和的形式，取前N阶模态阶数，即：

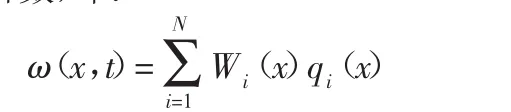
2.2 柔性机械臂的动力学模型建立

根据柔性机械臂的结构示意图，如图1所示。单连杆柔性机械臂任意一点P的位置坐标P（X，Y）为：

对式（5）求导，可得P点的速度表达式。对于柔性机械臂系统，总动能T包括驱动电机转轴的动能T1，连杆的动能T2和末端附加质量的动能T3。

连杆的动能T2：

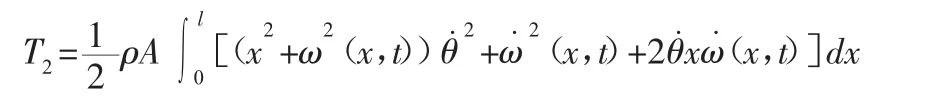
柔性臂末端附加质量动能T3：

考虑柔性机械臂的工作环境，忽略其重力势能，势能仅由连杆的弹性变形产生，则柔性机械臂系统总势能为：

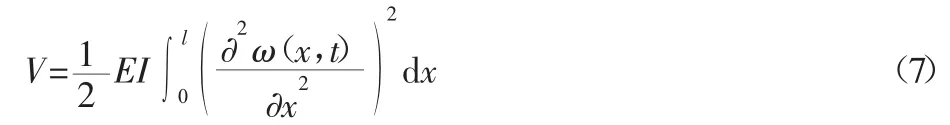
研究的柔性臂属于悬臂梁，根据弯曲梁振动固有振型的正交性，其模态振型函数的正交条件可表示为：

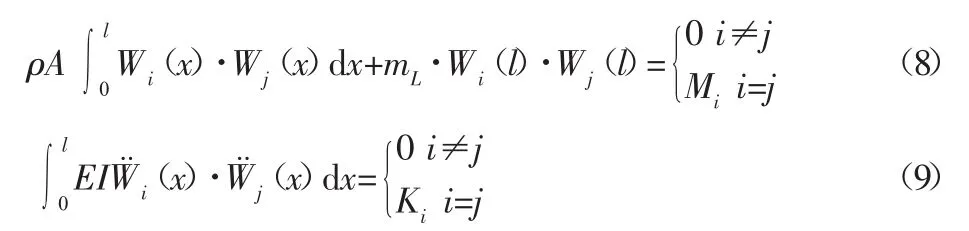
当 i=j时，有 Ki=Mi，Mi、Ki分别表示柔性机械臂第 i阶模态的广义质量和广义刚度。

将系统的总动能式（6）和总势能式（7）写成拉格朗日函数形式L=T-V，应用lagrange方程，并根据正交条件式（8）、（9）整理化简后得到末端有附加质量的柔性机械臂动力学方程：

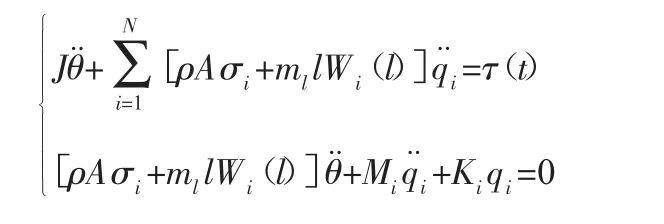
考虑阻尼因素，关节处的阻尼为粘性阻尼，结构阻尼采用结构动力学中的比例阻尼。由此可将上述得到的动力学方程改写成如形式：

式中：ξi—柔性臂第i阶弹性振动模态结构阻尼；ωi—柔性臂第i阶模态固有频率。

3 控制模型建立

3.1 状态空间表达式

不同模态阶数[11]下柔性机械臂的动力学响应，就末端弹性振动来看，第一阶弹性振动模态起主导作用，研究截取前一阶模态进行分析。设状态向量 x=［θ，q1，θ˙，q˙1］T，用状态空间方程：x˙（t）=Ax（t）+Bu（t）；y=Cx（t）表示柔性机械臂的动力学方程，得到柔性机械臂的状态空间表达式为

3.2 线性二次型（LQR）理论推导

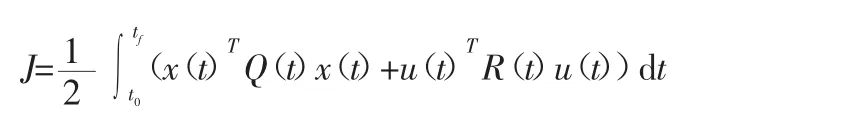
式中：矩阵 Q∈Rn×n，R∈Rm×m—非负定对称和正定对称常数加权系数矩阵。Q—对状态变量的加权矩阵。一般情况下，Q越大，控制系统达到稳定的时间越短；R—对输入量的加权矩阵。对于柔性机械臂系统来说，初始条件 x（t0）=［θ0，0，0，0］，终端条件 x（tf）=［θf，0，0，0］，设 t0=0，tf=∞。

保证性能指标J达到最小的最优控制量u*（t）的充分条件是：

式中：K=R-1BTP，为定常反馈增益矩阵；P—正定对称常系数矩阵，并满足Riccatti代数方程：

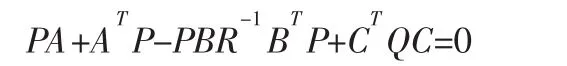
对于已建立的控制系统模型，采用现代控制理论中应用最成熟的线性二次型方法，对柔性机械臂的末端弹性运动进行振动控制。设计一个最优控制u（t），使如下性能指标J达到极小值：

4 遗传算法优化

遗传算法（Genetic Algorithm）是一类以模拟生物界自然进化规律演化而来的一种随机化、全局化的搜索寻优方法，其借鉴了生物进化过程中的遗传繁殖机制。具有良好的并行操作能力及全局的搜索寻优能力，并采用概率化的寻优方法，遗传算法被广泛应用在信号处理、智能计算、智能控制等领域。遗传算法一般包括编码解码、计算适应度值、遗传操作、参数控制等操作。

由于LQR控制的最优性由加权矩阵Q和R决定，Q矩阵的选取直接影响控制结果，故对加权阵Q进行寻优。因此可选取Q为四维半正定对角矩阵，R为一维正定矩阵。具体表示如下：

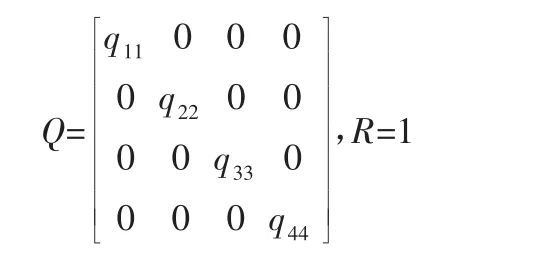
根据实践经验，将Q矩阵中4个参数变量的范围依次设置为 q11∈［1 2000］，q22∈［1 100］，q33∈［1 100］，q44∈［1 100］。

遗传算法的具体步骤如下：

Step1：确定待优化控制变量的约束范围并产生初始种群；

Step2：将初始种群中的每一个个体的值依次赋给加权矩阵Q的变量q11、q22、q33、q44，并求出对应的最优控制反馈增益矩阵K，根据式（10）求出最优控制输入量u*（t），在Matlab软件simulink环境下仿真系统的控制模型；

Step 3：将初始种群中的每个个体结合约束条件，分别计算每次参数下系统的动力学响应，求出柔性臂的振动量，经计算后输出每个个体的目标函数值J；

Step 4：将个体的适应度取为对应的目标函数J，根据计算结果判断是否满足遗传算法终止条件，如果不满足则进行遗传操作，否则直接跳到Step 6；

Step 5：进行遗传操作，设定初始群体大小M=20，终止进化代数G=100，交叉概率Pc=0.6，变异概率Pm=0.001。根据每个个体的目标函数值，按照给定的交叉概率和变异概率进行选择、交叉和变异遗传算子操作，产生新的种群个体，跳到Step 2，循环遗传算法的寻优过程；

Step 6：输出目标函数最小值所对应的种群个体值，并根据算法搜索得到的最优结果计算柔性机械臂的最优控制。

5 仿真实验

实验和计算用到的柔性臂为45号钢，柔性臂的具体结构参数，如表1所示。

表1 柔性机械臂几何物理参数Tab.1 Parameters of Flexible Manipulator

为验证遗传算法优化线性二次型最优控制器控制下的柔性机械臂末端弹性振动抑振效果，利用MATLAB软件进行数值分析和仿真实验。首先依据经验值仿真LQR控制器抑制柔性臂末端弹性振动，根据传统经验值选取 q11=1000，q22=10，q33=1，q44=1，此时所对应的目标函数值J=78.95，最优反馈增益矩阵K=［31.62，-14.75，4.30 ，1.86］。

遗传算法优化过程中获得的最优个体适应度函数值，如图2所示。从图中可以看出，随着种群的不断变化，最优个体适应度函数值不断变小，经过10代左右计算，得到最优个体。最终的最优个体为：q11=970，q22=76，q33=30，q44=32，优化后得到的最优反馈增益控制矩阵：K=［31.14，-61.71，7.69，1.47］。

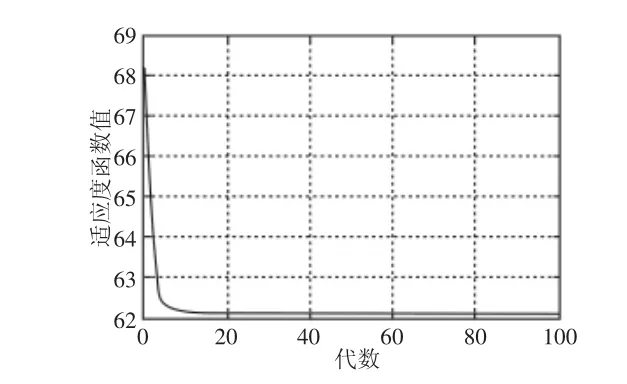
图2 遗传算法优化曲线Fig.2 Optimal Individual Value Variation of GA

优化前后柔性臂末端弹性振动的阶跃响应图，如图3、图4所示。端部转角的阶跃响应，如图5、图6所示。可以看出，优化后的柔性机械臂末端弹性振动得到了明显的抑制，稳定时间加快，端部转角的跟踪响应速度加快。

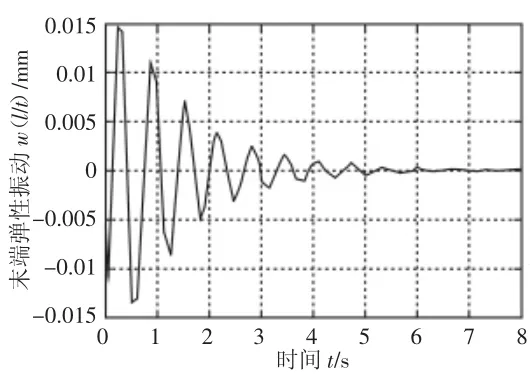
图3 优化前柔性机械臂末端变形Fig.3 Un-optimized Tip Deflection of Flexible Manipulator

图4 优化后柔性机 械臂末端变形Fig.4 Optimized Tip Deflection of Flexible Manipulator

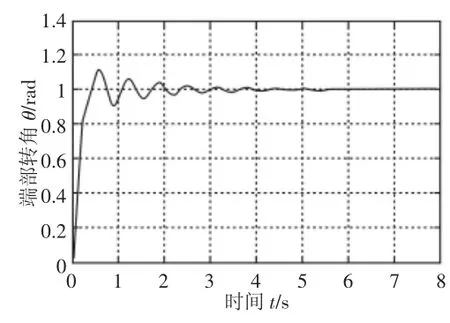
图5 优化前端部转角Fig.5 Un-optimized Angular Displacement Response of Flexible Manipulator

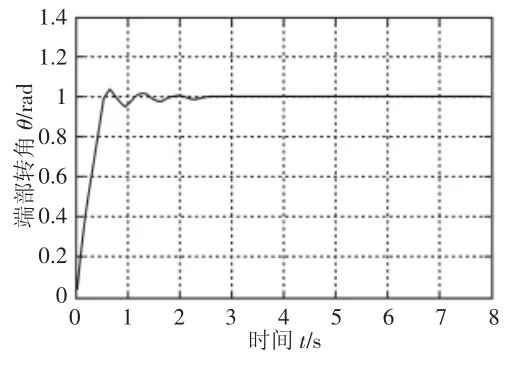
图6 优化后端部转角Fig.6 Optimized Angular Displacement Response of Flexible Manipulator

6 结论

对具有集中质量的单连杆柔性机械臂末端弹性振动进行研究，采用遗传算法优化线性二次型在振动控制中的权矩阵参数。实验结果表明，经遗传算法优化后得到的加权矩阵能够更好的权衡控制与端部响应的要求，与传统经验值相比，优化后的结果能有效抑制末端弹性振动，加快振动衰减的同时系统端部定位速度更快，验证了该方法的有效性。