机器人运动中六维力传感器的重力补偿研究

王志军，韩静如，李占贤，刘立伟

（华北理工大学 机械工程学院，河北 唐山 063009）

1 引言

六维力传感器能够检测大小和方向不断变化的三维力和三维力矩信息，一般安装在工业机器人末端，协助机器人完成力/位置控制、轮廓跟踪、轴孔配合等一些精细复杂的操作，在机器人中具有广泛应用[1-3]。但是，六维力传感器在随机器人运动的过程中，由于其位姿不断发生变化，同时受安装在传感器上的操作工具重力的影响，传感器的零位值也会随之不断变化，这就导致传感器测量上产生一定偏差，降低了其测量精度，进而影响机器人的操作。因此，有必要对机器人运动中的六维力传感器进行重力补偿。

关于不同情况下的重力补偿，国内一些学者也分别进行过理论算法推导或相关实验研究等，并取得了一定的研究成果。文献[4]提出了基于最小二乘法的参数识别方法，可用于对机器人臂的重力补偿；文献[5]采用矢量分解的方法推导出一种机器人的重力补偿算法；文献[6]利用拉格朗日方程的方法对机构进行重力补偿的理论计算，实现了对力觉交互设备的重力补偿；文献[7]通过对机器人建立动力学方程，分析得出重力补偿可使控制器克服重力，从而使机器人到达期望位置。以上这些研究从不同出发点和落脚点，根据各自不同情况分析或推导了机械臂重力补偿的算法、验证及控制等问题，证明了重力补偿在机器人操作中的重要和必要性，对重力补偿研究具有一定的学习和借鉴意义。

针对机器人姿态变化导致末端工具重力影响六维力传感器零位值的问题，在结合前人研究的基础上，提出了一种简单有效的重力补偿算法，利用机器人各连杆变换矩阵和不同坐标系的力坐标变换，消除六维力传感器测量中工具重力的影响，能够实时补偿传感器的零位值，使传感器在机器人运动过程中也能检测出末端实际所受外力的大小，从而使机器人能够完成更加精密的操作任务。

2 重力补偿算法推导与分析

工业机器人在一些主动柔顺作业中，机械臂的腕关节上会通过一个六维力传感器来连接末端执行工具，完成各项操作任务[8]。传感器能够测得末端工具所受的外力/力矩，进而反馈给控制系统控制机器人实现柔顺运动。在这种情况下，为了消除工具自身重力对传感器示数造成的影响，得到准确的外力反馈信息，我们需要以机器人本体、六维力传感器、末端工具为研究平台，推导和研究相应的补偿算法对传感器测量结果进行重力补偿。

2.1 机器人各连杆的变换矩阵

以某公司的TAWERS-1800机器人为研究对象来推导重力补偿算法，该机器人共有六个关节，每个关节均为转动关节。

由D-H法建立基坐标系｛0｝及各关节坐标系｛i｝，如图1所示，同时定义各连杆的参数与变量，并列出连杆参数表，如表1所示。

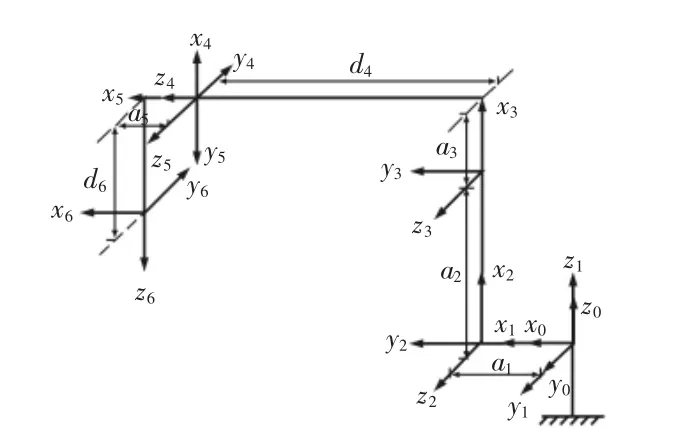
图1 机器人的连杆坐标系Fig.1 Connecting Rod Coordinate System of the Robot

表1 机器人的连杆参数Tab.1 Connecting Rob Parameters of the Robot

连杆变换矩阵i-1iT的通式为：

根据表1的各连杆参数，带入上述通式（1），可得到各连杆的位姿变换矩阵将以上各连杆变换矩阵相乘，可得到机器人腕部坐标系相对于基坐标的位姿变换矩阵：

2.2 重力补偿算法的推导

定义传感器坐标系｛S｝及工具坐标系｛T｝与空间基坐标系｛0｝的位姿关系，如图2所示。

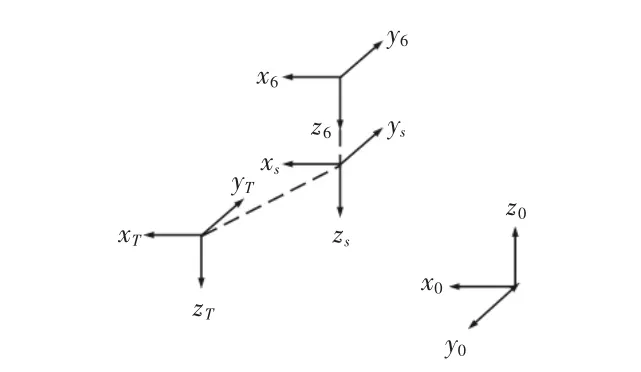
图2 机器人传感器及末端工具坐标系Fig.2 Sensor and Tool Coordinate System of the Robot

传感器坐标系｛S｝相对机器人腕部坐标系｛6｝沿z6正方向平移距离h，工具坐标系｛T｝与传感器坐标系｛S｝姿态相同，坐标原点 OT到坐标系｛S｝的 x 轴，y 轴，z轴投影分别为 px，py，pz，则传感器及末端工具与相邻坐标系的变换矩阵分别为：

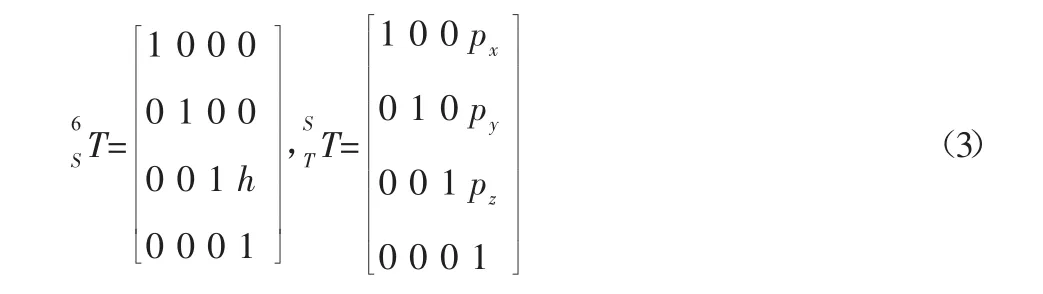
由以上各位姿变换矩阵，最终可以得到机器人末端工具相对空间基坐标系｛0｝的变换矩阵为：

设机器人末端工具重力的大小为G，方向沿空间基坐标系｛0｝的z0轴负方向，重心在工具坐标系｛T｝的坐标原点，则在基坐标系｛0｝下，重力的三维力分量矩阵恒为：0f=［0 0 G］T。

机器人运动过程中，随着末端工具的位置和姿态不断改变，其重力在工具坐标系｛T｝下的三维分量会发生变化，相应地，传感器的零位值也会随之变化。因此，我们需要推导出末端工具重力在传感器坐标系｛S｝下的三维力和力矩值，即在测量机器人所受外力之前，对传感器零位位置的重力补偿值。

由式（4）可知工具坐标系相对于基坐标系的旋转矩阵，则重力在工具坐标系｛T｝下的三维力分量为：

因为重心在工具坐标系｛T｝的坐标原点，所以重力在｛T｝坐标系三轴方向的力矩为0。因此，重力在｛T｝坐标系下的六维力/力矩为：

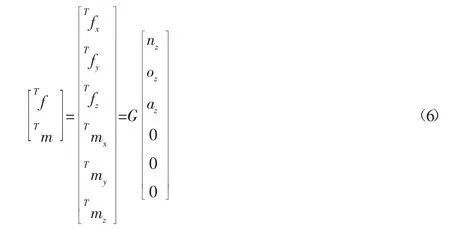
根据文献[9]中力和力矩矢量在不同坐标系中的变换关系，可得重力在传感器｛S｝与工具｛T｝坐标系中的关系式为：

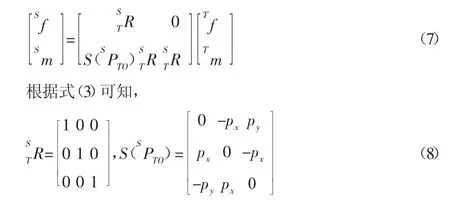
由此可得重力在传感器坐标系｛S｝下的六维力/力矩，即最终所需要的重力补偿值为：

六维力传感器测得的力和力矩值，是工具自身重力与其所受外力共同作用的结果。通过式（9）中求得的操作工具重力随机器人位姿变化在六维力传感器上的力/力矩值，即需要进行的重力补偿值，对传感器测得示数进行补偿，能够消除由机器人姿态变化引起的末端工具重力影响，提高六维力传感器的测量精度。

当机器人处于某一位姿下，末端工具受到外力时，如果六维力传感器上力与力矩分量的读数分别用Sfc、Smc表示，那么经过重力补偿，最终实际机器人末端所受外力/力矩信息f、m为：

由式（10）可以看到，通过重力补偿，我们可以准确得到机器人末端执行工具所受的外力/力矩，将末端工具实际所受外力反馈到控制系统，就能控制机器人按照操作人员的意图实现主动柔顺操作。

2.3 重力补偿算法的数值算例

根据上文推导的重力补偿算法式（9），下面结合具体算例，运用MATLAB软件进行重力补偿理论推导的数值计算与分析。由TAWERS-1800机器人的结构尺寸，可知各连杆变换所需参数 a1，a2，a3，d5，a5，d6的值；设机器人末端工具重心相对传感器坐标系的位置为SPTO=［115-50 55］T，重力大小为100N，沿基坐标系｛0｝的Z0轴负方向；在机器人各关节工作角度范围内，取θ1∈［0，-π/6］rad，θ2∈［-π/2，-2π/3］rad，θ3∈［0，-π/6］rad，θ4∈［0，-π/6］rad，θ5∈［π/2，π/3］rad，θ6∈［0，-π/6］rad 各关节转动角速度为3rad/s。将以上参数带入式（9），运用MATLAB编程计算并生成重力在传感器坐标系x，y，z三个方向的力和力矩补偿的理论计算值，如图3所示。

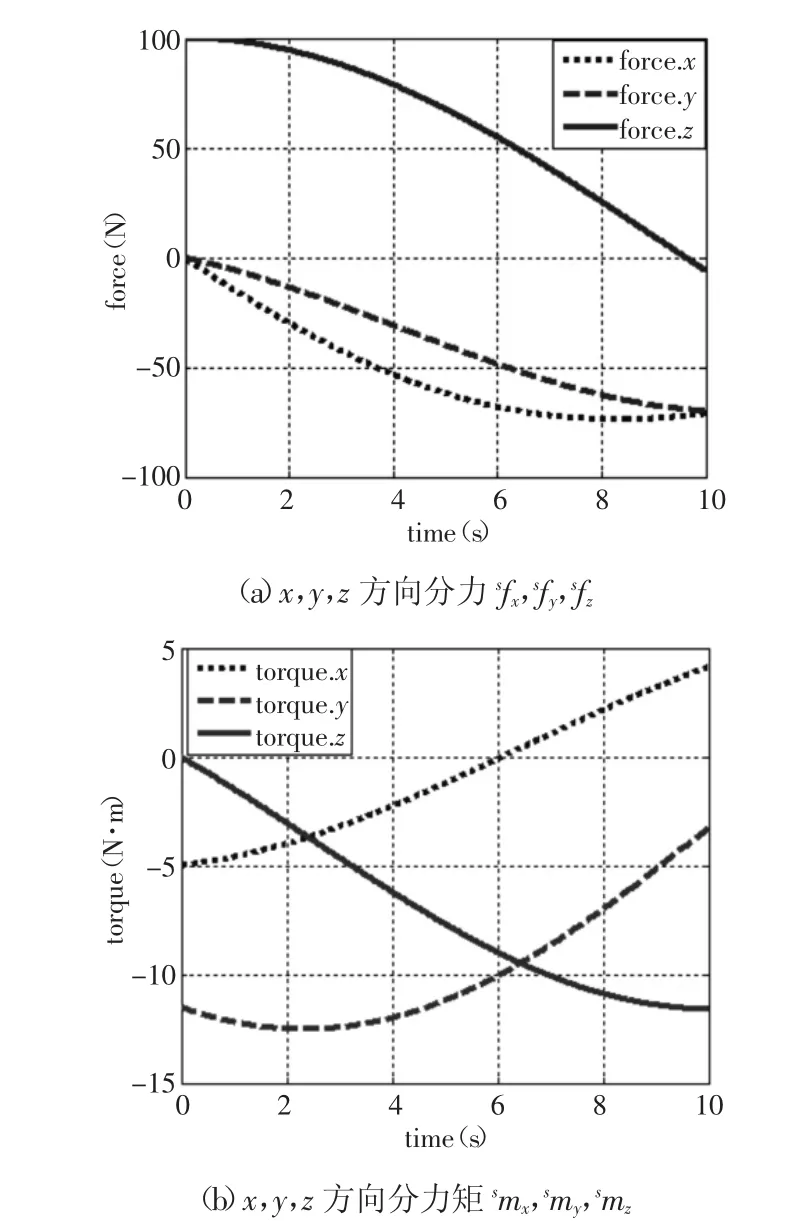
图3 重力补偿的计算值Fig.3 The Calculated Value of Gravity Compensation

从图中可以看出，随着机器人的运动，工具重力在六维力传感器上的力和力矩随机器人的姿态不断变化，通过重力补偿结果能够对六维力传感器的零位值进行实时补偿，从而消除了由机器人姿态变化引起的末端工具重力影响，提高了六维力传感器的测量精度。

3 重力补偿仿真分析

Adams具有强大的运动学和动力学仿真功能，使用该软件可以产生复杂机械系统的虚拟样机，真实地仿真其运动过程，进行相关分析[10]。运用Adams软件进行重力补偿相关仿真，目的是希望通过对机器人的运动仿真，测得在机器人运动中传感器所在坐标系的六维力/力矩值，与我们推导出的重力补偿算法的理论计算值进行比较，验证推导的重力补偿算法是否正确。

首先将简化的TAWERS-1800机器人三维模型导入Adams中，如图4所示，然后定义各零部件的材料、质量等相关属性，使仿真模型尽可能与TAWERS-1800机器人实际物理属性相近，最后定义模型的各种约束及驱动，进行运动仿真。

图4 机器人仿真模型Fig.4 Robot Simulation Model

按照2.3节所描述的运动，定义机器人各关节旋转驱动函数为：Funcition（time）=3.0d*time，设置仿真时间为 t=10s，仿真步数step=500进行仿真，并测量传感器坐标系三个方向的力和力矩，生成六维力传感器的力与力矩测量曲线，如图5所示。

图5 重力补偿的测量值Fig.5 The Measured Value of the Gravity Compensation

通过与图3对比可知，六维力传感器的力和力矩仿真测量曲线与重力补偿的理论计算值基本一致，从而验证了推导重力补偿算法的正确性。

4 结论

通过对机器人、六维力传感器及其末端执行工具的位姿变换进行分析，推导得到一种简单有效的六维力传感器重力补偿算法，并运用MATLAB、Adams软件对机器人运动中六维力传感器的重力补偿分别进行理论计算与仿真分析，得到了末端执行工具重力随机器人位姿变化，实时作用在六维力传感器上的力/力矩值曲线，通过比较可以看出重力补偿算法的理论计算与仿真测量的结果曲线基本一致，最终验证了该重力补偿算法的正确性和可行性。该重力补偿算法能够消除由机器人姿态变化引起的末端工具重力影响，提高六维力传感器的测量精度，实时获得机器人运动中实际作用在机末端执行机构的外力/力矩信息，进而反馈给控制系统以实现机器人的主动柔顺运动。