磁粉制动器数学建模与控制方法研究
袁宇凤 ,任 芳 ,杨兆建
(1.太原理工大学 机械工程学院,山西 太原 030024;2.煤矿综采装备山西省重点实验室,山西 太原 030024)
1 引言
磁粉制动器是以磁性材料作为工作介质,通过控制激磁电流来实现控制转矩和制动。在现阶段各类型的加载设备中,由于磁粉制动器的输出与输入整体呈线性关系而与其他因素转速等无关,所以磁粉制动器在纺织、印刷、造纸、速度和位置控制系统中,作为系统的执行部件,其应用较为广泛,但由于磁性材料自身磁滞效应的影响,使得其加载质量与快速性都有所降低[1]。对于磁粉制动器的研究,文献[2]提出了一种新的磁电路建模方法,即基于梯度修复的粒子群算法;文献[3]提出应用大尺寸磁性粒子(小钢辊)来产生更高的制动力矩的新方法。而国内控制算法的研究较多,针对磁粉制动器这类存在滞后的一阶惯性系统,因为被控量不能实时响应系统的实时输入,导致超调量过大,调整时间过长,使得控制系统的稳定性和快速性都会明显变差,从而导致对系统控制算法的设计难度大大增加,文献[4-6]研究了各类算法对磁粉制动器的控制,却都存在一定的局限性。在分析其工作原理的基础上,对磁粉制动器的数学模型进行了建模分析,应用PID控制理论、施密斯预估控制和模糊控制理论进行了控制算法设计与研究,并在Matlab中实现了计算机仿真。
2 磁粉制动器工作原理
磁粉制动器传递转矩的原理是基于电磁学,如图1所示。转子和定子之间形成一个同心的圆柱形的间隙,该间隙中装入磁粉材料,在转子随着输入轴旋转而线圈没有通电励磁的情况下,间隙中的磁粉在向心力的作用下被甩在转子的内壁上,此时转子与定子完全脱离,转子空转,不传递制动力矩。在线圈通电励磁的情况下,线圈一旦通电,则会有磁力线产生,磁粉迅速磁化,立即把定子和转子表面连接起来,当转子随着输入轴转动时,就必须克服磁粉与定子、磁粉与转子表面之间的摩擦力,而所有的摩擦力就形成了抑制转子转动的制动力矩[1]。制动力矩的大小随着输入电流的增大而增大。

图1 磁粉制动器结构图Fig.1 Structure of Magnetic Particle Brake
3 数学模型
数学模型能够定量地描述系统的动态特性,揭示系统的结构、参数与动态特性之间的关系,被控对象的数学模型对控制算法的研究具有指导作用,在如图一所示的磁粉制动器模型中:设内定子的外径为Dm和宽度为Lm,根据莫尔-库仑原理[7],则其传递的力矩T为:

式中:B—磁粉间的磁感应强度;μ0—气隙磁导率;μδ—磁粉槽内磁粉磁导率。
式(1)线性化、拉氏变换得

在制动器磁路中,由磁场欧姆定律得:

式中:N—线圈匝数;I—线圈电流;Ri—铁磁阻;Rδ—间隙及磁粉总磁阻;L—电感量;Sδ—磁粉填充区域垂直于磁路的有效面积

由于磁粉材料的滞后性,磁粉制动器的数学模型为:

根据建立的数学模型,放大系数K和时间常数T与磁粉及间隙磁阻、磁导率,电感量等因素有关,而磁粉制动器在使用过程中,由于会发热,这些参数会随着使用时间而发生变化,所以无法确定其精确的数学模型,又磁粉具有滞后性,故对控制算法提出来更高的要求。
4 控制算法
4.1 施密斯预估控制
施密斯预估控制是特别针对具有纯滞后性质的被控对象而设计的一种控制算法,其控制原理是通过一个补偿环节,使得纯滞后部分在闭环控制回路之外,从而不影响闭环系统的稳定性,但传统的施密斯预估控制系统中的控制器是PID控制,这种算法对数学模型的精确匹配依赖程度非常高,一旦与被控对象的模型失配,施密斯预估控制算法就很难取得良好的控制效果,而磁粉制动器在使用的过程中,由于其参数的时变性,很难得到其精确的数学模型,只能根据实验数据获得,故针对磁粉制动器这样的系统,传统的施密斯预估控制存在一定的局限性。施密斯预估控制的系统框图[8],如图2所示。

图2 施密斯预估控制系统框图Fig.2 The Block Diagram of the Smith Predictor Control System
图中:G(s)e-τs—磁粉制动器的数学模型;G(s)(1-e-τs)—施密斯预估控制器的传递函数,它和和调节器D(s)构成了纯滞后补偿器。经施密斯预估补偿后的系统闭环控制的等效形式,如图3所示

图3 施密斯预估控制系统等效框图Fig.3 The Equivalent Block Diagram of the Smith Predictor Control System
4.2 模糊控制
模糊控制是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一类控制策略,是结合专家的知识和思维,进行学习与推理、联想和决策的过程,由于其不需要被控对象的精确数学模型的特点,对磁粉制动器这类无法获得其精确数学模型的控制对象是一种较为理想的控制方式[9],但由于磁粉制动器的滞后性会导致模糊输出的控制量与控制系统实时所需的控制量有一段时间上的滞后,所以对于这类时滞系统来说,传统的模糊控制的控制效果不太理想,而施密斯预估控制的本质就是解决控制系统中滞后性所带来的问题,于是将模糊控制与施密斯控制相结合,组成模糊施密斯控制,而模糊控制的本质是对偏差信号进行比例与微分控制,PD控制会使系统产生较大的静差,所以在此基础上,对模糊控制的输出进行积分作用,用来消除静差,进而达到所需的控制目标。
设计模糊控制系统为二维模糊控制器,选择系统输出与给定值间的误差e及误差变化率ec作为输入变量,将输入变量e、ec及控制量u的模糊集及其论域定义如下:
e、ec的模糊集均为{NB,NM,NS,ZO,PS,PM,PB},论域均为{-3,-2,-1,0,1,2,3},u 的模糊集为{NB,NM,NS,ZO,PS,PM,PB},论域为{-6,-5,-4,-3,-2-1,0,1,2,3,4,5,6},隶属函数均选择三角型隶属函数。针对滞后系统的特点,根据控制量需要提前响应的要求,结合经验规则,建立模糊控制规则,如表1所示。
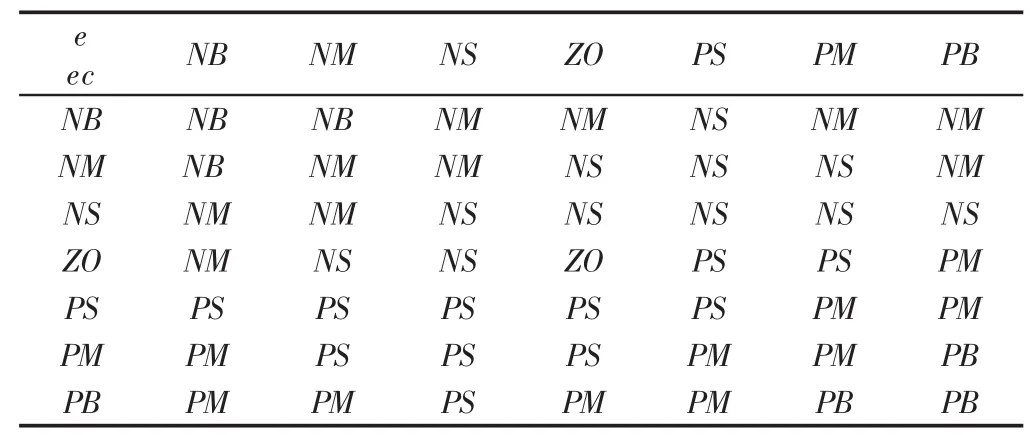
表1 模糊控制规则表Tab.1 Fuzzy Control Rule Table
系统输出与给定值间的误差e的基本论域是根据每次采样获得的实际过程值所决定的,其值不一定在相应语言变量的论域内,故需要将实际输入变量的基本论域变换到其语言变量的论域内,即所谓的输入量化。对误差e来说,需将输入变量e乘上一个量化因子Ke,使得e的论域转换到所定义的[-3,3]。同样,输入变量ec也需要乘一个相应的量化因子Kec,将ec的论域也转换到定义的[-3,3]。相反,输出也需要输出量化,即输出语言变量u的论域在模糊控制算法中定义为[-6,6],其需要通过乘一个输出比例因子,进而将定义的u的论域转化为实际输出变量的论域。
量化因子Ke及Kec和比例因子Ku对模糊控制系统的控制品质有较大的影响。一般情况下,Ke越大,系统超调就会增大,相应的过渡过程时间也就越长,Ke越小,控制系统变化率下降,稳态精度随之降低;Kec越大,系统的快速性降低,Kec越小,系统的响应速度越快,但随之带来的是超调量增加。输出比例因子Ku越小,控制系统的动态响应过程变慢,而Ku越大,系统的控制作用就越强,但选择过大易导致系统发生振荡[10]。
4.3 仿真模型及结果
为了实现磁粉制动器在加载系统中的高精度加载与快速响应,首先将所设计的PID控制和引入积分作用的模糊施密斯控制在Matlab的Simulink模块中进行计算机仿真,进而为磁粉制动器的计算机控制提供理论支持与指导。
常规PID控制的仿真模型设计,如图4所示。在Chien-Hrones法参数整定的原则上,再经过反复试验,确定PID控制器的初始参数值为:Kp=0.3,Ki=0.15,Kd=0.126。
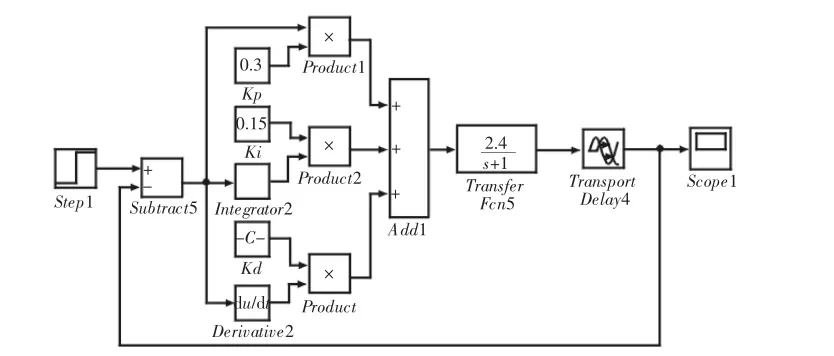
图4 常规PID控制的仿真模型Fig.4 Simulation Model of Conventional PID Control
引入积分环节的模糊施密斯控制的仿真模型,如图5所示。根据误差及误差变化率信号及多次试验的结果,确定量化因子Ke=2.6,Kec=1.98,u 的比例因子 Ku=0.4。

图5 引入积分环节的模糊施密斯控制的仿真模型Fig.5 Simulation Model of Fuzzy Integral Smith Predictor Control
在输入为阶跃信号时,得到的系统仿真曲线,如图6所示。

图6 仿真结果曲线图Fig.6 Curve of Simulation Results
从图6的仿真结果可以看到:模糊施密斯控制虽无超调,响应也快,却达不到稳态值。PID控制的超调量为11.4%,而引入积分环节的模糊施密斯控制基本没有超调,时间响应也更快,而因为PID控制对数学模型精确性的高要求,进一步证明该算法无论从适用性还是控制效果都更为合适,这为磁粉制动器在加载系统中的计算机控制奠定了理论基础。
5 结论
建立了磁粉制动器的数学模型,为惯性滞后系统。由于其系统的时变性与滞后性,阐述了各控制算法的优点与不足,研究表明:对于磁粉制动器这样的时滞系统,施密斯预估控制消除了纯滞后部分对控制系统品质的影响,模糊控制解决了磁粉制动器数学模型不精确的问题,提出的对模糊施密斯的输出进行积分作用的算法,消除了控制系统所产生的静差。三种控制算法的结合,使得磁粉制动器的加载具有很好的可控性,并且,和常规的PID控制相比较,引入积分环节的模糊施密斯控制在控制系统快速性、稳定性和精确度方面都有很大的提高,故引入积分作用的模糊施密斯控制器对磁粉制动器这类时滞系统具有很强的适用性与实用性。

