基于Stick-slip振动试验的Stribeck摩擦模型参数研究

黄 博，吴元科，王润兰，王晓翠，欧阳华江，莫继良*

(1.西南交通大学 摩擦学研究所，四川 成都 610031；2.轨道交通运维技术与装备四川省重点实验室，四川 成都 610031；3.利物浦大学 工程学院，英国 利物浦 L693GH)

Stick-slip振动是一种广泛存在于工程应用和日常生活中的摩擦振动现象，是由动静摩擦之间存在间歇性的变化引起的一种自激跳跃运动[1-2]。Stick-slip振动通常会引起不必要的振动噪声、增加零部件之间的磨损甚至引起零件松动，降低设备使用精度和寿命等问题[3-4]。因此，针对Stick-slip振动的研究一直倍受关注。

由于Stribeck摩擦模型能够很好地体现相对速度和摩擦系数之间的关系，并且具有能描述静摩擦、Stribeck效应等摩擦现象和参数易于辨识的特点，因此被广泛运用于Stick-slip振动研究。Xiang[5]等利用Stribeck模型描述了轴承与轴颈间的Stick-slip运动，分析了间隙大小、静摩擦系数和滑动摩擦系数对Stick-slip运动的影响特性。李小彭[6]等基于Stribeck摩擦模型研究了自激系统振动的分岔与混沌特性。王延忠[7]等建立盘式摩擦副的动力学方程，基于Stribeck模型研究了系统关键参数对系统Stick-slip振动的影响。王宇[8]建立了一个三自由度盘式系统模型，采用Stribeck模型研究了制动法向力对系统混沌振动的影响。

然而，以往大多数关于Stribeck模型的Stick-slip振动研究都是基于理论计算[5-10]，不能体现实际运行时法向力和转速等参数的变化对系统Stick-slip振动和Stribeck摩擦模型的动、静摩擦系数和衰减系数的影响。考虑到摩擦过程中振动非常复杂且对工况参数的变化敏感性强，任何微小的工况参数的改变都可能导致摩擦过程中的Stick-slip振动发生显著的变化。因此，如果能结合试验分析手段，以Stick-slip振动试验中变化的工况参数为载体，深入理解工况参数对Stribeck摩擦模型参数的影响规律，则可以更加准确地分析和预测摩擦过程中Stick-slip振动行为。

为此，研究以销-盘接触的方式进行不同工况(法向力、摩擦盘转速)的Stick-slip振动试验，分析试验中的法向力和摩擦盘转速对系统Stick-slip振动的影响特性。分析试验结果，辨识得到Stribeck摩擦模型的参数，进一步分析法向力和转速对Stribeck摩擦模型中参数的影响。研究结果不仅丰富了基于Stick-slip振动行为的Stribeck摩擦模型理论体系，亦具有重要的工程应用价值。

1 试验装置及试验参数

1.1 试验装置

图1 试验装置示意图

试验研究基于CETR UMT-3摩擦磨损试验机进行销-盘试验，试验装置如图1所示，主要由摩擦盘试样、摩擦块试样、摩擦块夹具、缓冲装置、二维力传感器、二维移动平台以及采集分析设备组成，试验设备的各个部件用螺钉紧密连接。二维力传感器(灵敏度为0.025 N，量程为5～500 N)用于记录试验过程中的摩擦力和法向力，激光测振仪(型号为Polytec PDV-100，灵敏度为8 mv/mm/s，量程为±500 mm/s，频响为0.5～22 kHz)用于记录试验过程中摩擦块上振动速度，测点位置及测试方向(x方向)如图1中所示，采样频率均设置为20 kHz。

1.2 试验样品参数及试验工况

摩擦盘试样选用锻钢加工成直径为25 mm，厚度为3 mm的圆盘，粗糙度(Ra)为0.06 μm。摩擦块试样材料取自汽车制动片，加工成9 mm×9 mm×25 mm的销，粗糙度(Ra)为0.4 μm。试验过程摩擦块中心到摩擦盘中心距离即摩擦半径为6.45 mm，如图1所示。

每次测试前，用酒精和丙酮对试验样品进行清洗。试验开始时，二维移动平台带动摩擦块试样向下移动与摩擦盘试样接触达到预先设定的法向力，之后法向力保持恒定；然后摩擦盘开始从静止均匀增加到指定转速后保持恒定直到试验结束，每次试验时间为2 min，试验在150 N、180 N和200 N三种法向力，2 rpm、4 rpm、6 rpm、8 rpm和10 rpm五种转速共15种工况下进行。为确保试验的可靠性，每个工况的试验重复3次，所有试验在湿度为50±10% RH，温度为24～27 ℃的环境中进行。

2 Stribeck摩擦模型方程

图2 Stribeck模型中摩擦系数随相对速度变化曲线[11]

Stribeck摩擦模型方程的表达式主要有分式形式和指数形式，预实验发现指数形式与试验结果的重合度比分式形式更高，于是选择Bo和Pavelescu[11]所提出的指数形式，其表达式为：

μ(vr)=[μk+(μs-μk)*exp(-α|vr|)]sign(vr),

(1)

式中，μk为动摩擦系数；μs为静摩擦系数；vr为相互接触物体间的相对运动速度；α为摩擦模型中的指数衰减因子。一般的vr-μ曲线如图2所示。下面分别根据不同法向力和不同速度下的试验结果对Stribeck摩擦模型的方程中的参数进行辨识。

3 法向力对Stribeck模型参数的影响

3.1 不同法向力下的振动特性

首先研究法向力对Stick-slip振动特性的影响。不同法向力下摩擦块速度和位移时域信号如图3所示。摩擦盘转速为2 rpm时不同法向力下摩擦块振动速度随时间变化曲线如图3a所示。由图3a可知，摩擦块的振动速度出现了明显的周期性的突变现象。在速度的非突变状态时，速度的大小与摩擦盘在摩擦半径处的线速度相等，此时摩擦盘和摩擦块之间处于Stick状态;当摩擦块速度发生突变时，摩擦块和摩擦盘在接触点处的线速度不再相同，则处于Slip状态。由此可以判定在三种法向力下，系统处于周期性的Stick-slip运动。并且，在摩擦盘转速相同的条件下，法向力越大，Stick-slip振动的周期越长。

进一步利用MATLAB中的频域积分函数Iomega对速度信号进行积分，得到对应的位移随时间变化曲线如图3b所示。由图3b可知，摩擦块的位移曲线呈现出周期性的增加和下降趋势。结合图3a、图3b得到不同法向力下摩擦块运动相图如图4所示。由图4可知，法向力为150 N时，摩擦块运动的极限环最小；法向力为200 N时，摩擦块运动的极限环最大，Stick-slip振动最明显。

图3 不同法向力下摩擦块速度和位移时域信号

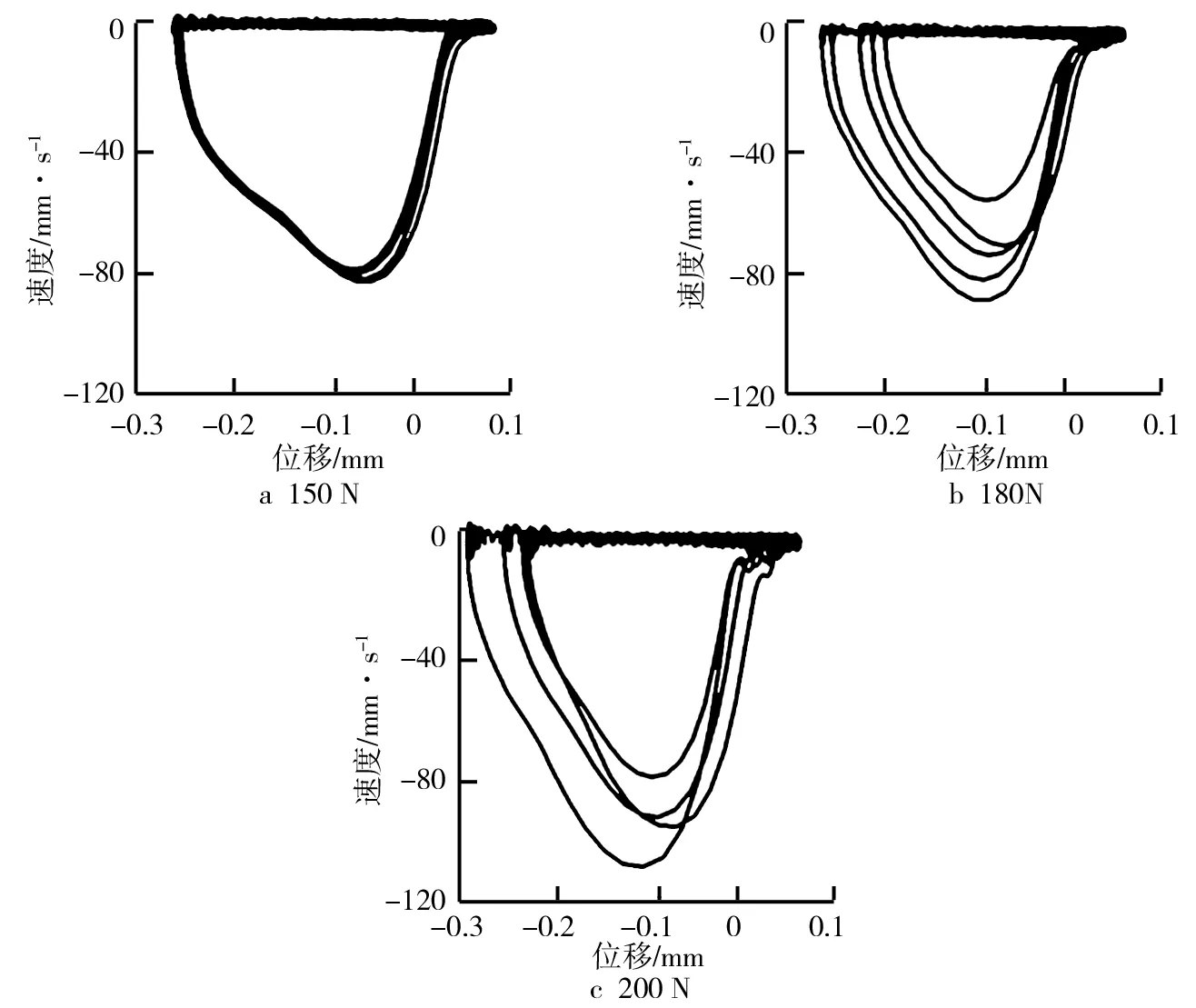
图4 不同法向力作用下的摩擦块运动相图

3.2 不同法向力下的静摩擦特性

为了得到更加准确的用于分析系统Stick-slip振动特性的摩擦模型，进一步分析不同法向力下的静摩擦系数。加载初始阶段转速为2 rpm时不同法向力下摩擦块所受摩擦力和法向力的时域信号如图5所示。由图5a可知，试验开始后摩擦力逐渐增大，在第3 s时摩擦力达到峰值，之后摩擦力开始出现震荡现象，系统开始周期性的Stick-slip运动；法向力在第3 s时出现了明显的下降，之后为周期性的波动，波动的周期与摩擦力的波动周期一致。在第3 s时摩擦块所受到的最大静摩擦力为30.312 N，对应的法向力为150.361 N，可以得到静摩擦系数μs为0.201。

同样的根据图5b、图5c可以得到法向力为180 N和200 N条件下的静摩擦系数分别为0.201和0.203。由此可以得到，在其他条件保持一致的条件下，法向力的改变对系统的静摩擦系数的影响很小。

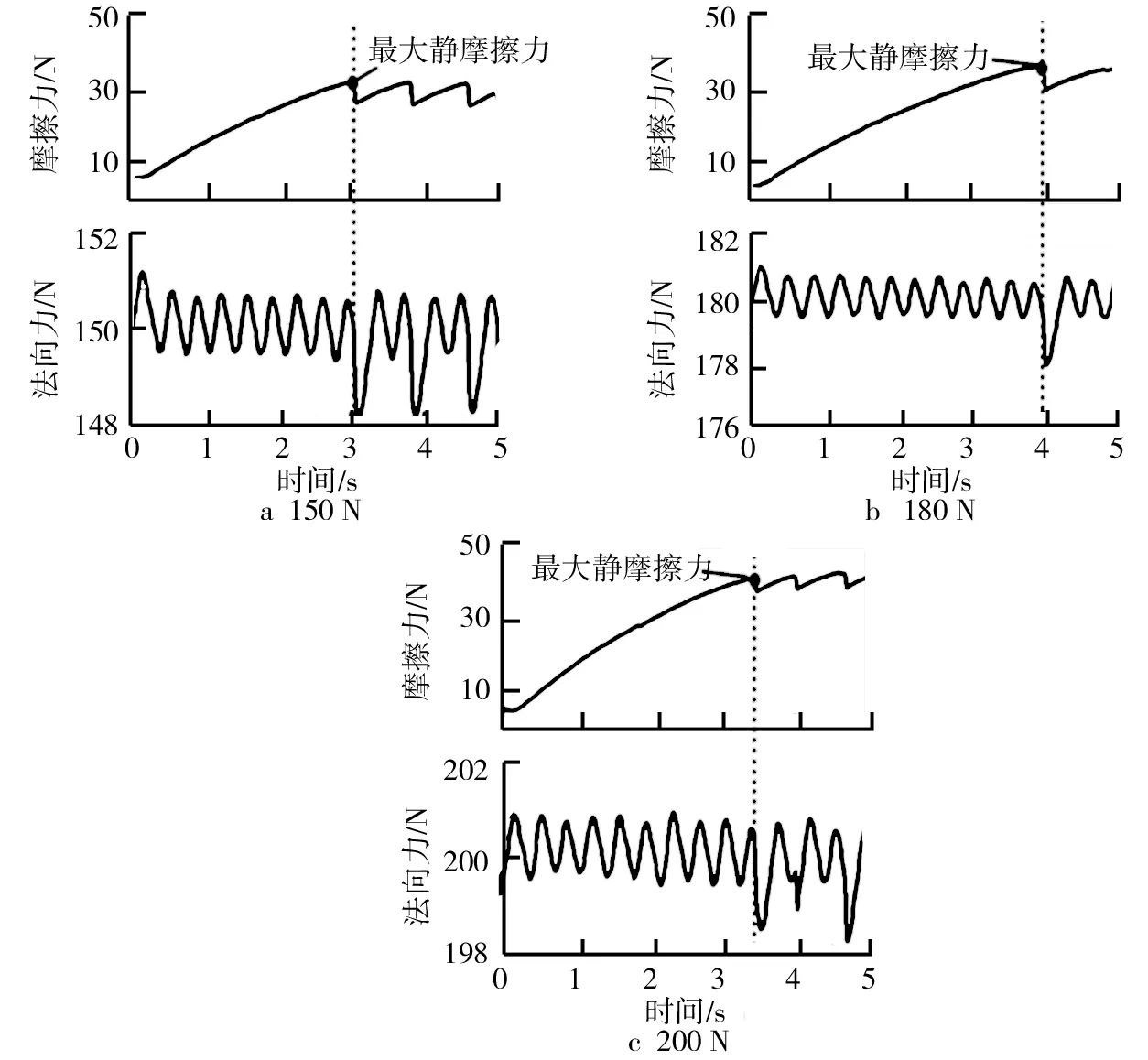
图5 不同法向力下初始阶段摩擦力和法向力时域曲线

3.3 不同法向力下的动摩擦系数及衰减系数

转速为2 rpm时不同法向力下稳定阶段的摩擦比率和相对运动速度随时间变化的曲线如图6所示。其中摩擦比率为同一时刻摩擦力和法向力的比值，相对速度为摩擦盘上摩擦半径处的线速度与摩擦块运动速度的差值。从图6中可以看出，摩擦比率在运动过程中是周期性变化的，Stick阶段，摩擦比率是随时间逐渐增大的，Slip阶段，摩擦比率逐渐减小。对比不同法向力下的摩擦比率可以发现，随着法向力增大摩擦比率波动的幅值逐渐减小。

图6 不同法向力下摩擦比率和相对速度时域曲线

通过分析发现，当相对运动速度不为0时，摩擦比率产生明显变化，此时处于滑动状态，摩擦比率为动摩擦系数，因此猜测动摩擦系数和相对运动速度之间存在某种联系。通过对比不同法向力下三次重复试验结果中Slip阶段的摩擦系数和相对速度之间的关系，得到动摩擦系数与相对运动速度间的关系如图7所示。在三个法向力下，动摩擦系数均随着相对运动速度增加而减小；特别地，在相对速度较低阶段，呈现出摩擦系数随相对速度增加而减小的负斜率现象，当相对速度增加到一定数值，摩擦系数几乎不再随相对运动速度改变，相对运动速度越大，动摩擦系数随速度变化得越缓慢。法向力为150 N时，稳定时动摩擦系数约为0.160；法向力为180 N时，稳定时动摩擦系数约为0.175；法向力为200 N时，稳定时动摩擦系数约为0.180。可以看出法向力越大，稳定时动摩擦系数越大，并且动摩擦系数和相对速度的关系符合Stribeck摩擦模型。

为了确定Stribeck摩擦模型方程式(1)中的衰减系数，利用MATLAB对三组试验结果进行拟合，得到不同法向力下衰减系数α及Stribeck摩擦模型的摩擦系数曲线(图7中实线)。最终得到不同法向力下Stribeck摩擦模型的动、静摩擦系数及衰减系数如表1所示。

由此可以得到，在同一个摩擦系统中，法向力的改变会影响Stribeck摩擦模型的动摩擦系数和衰减系数，增大法向力会使得动摩擦系数变大，衰减系数减小。而法向力对静摩擦系数的影响很小。

图7 不同法向力下摩擦系数与相对运动速度的关系

表1 不同法向力下Stribeck摩擦模型方程参数

4 转速对Stribeck模型参数的影响

4.1 不同转速下系统的振动特性

进一步研究摩擦盘转速对系统振动的影响。不同速度下摩擦块的速度和位移时域曲线如图8所示。由图8a可知，法向力为150 N时不同转速条件下的摩擦块的速度和位移随时间变化曲线如图8a所示。当摩擦盘的转速为2 rpm、4 rpm和6 rpm时，摩擦块的振动速度出现了明显的周期性的突变现象，在速度的非突变状态时，摩擦块速度的摩擦盘在摩擦半径处的线速度相等，由此可以判定系统在转速为2 rpm、4 rpm和6 rpm时处于Stick-slip运动状态。当转速为8 rpm和10 rpm，摩擦块速度的突变现象消失，并且摩擦块的速度和摩擦盘在摩擦半径处的线速度不同，此时系统处于连续滑动状态。通过频域积分的方法得到摩擦块的位移曲线如图8b所示。由图8b可知，系统处于Stick-slip振动时，摩擦块的位移曲线呈现出周期性的增加和下降趋势。并且，摩擦盘的转速越大，位移波动的幅值越小。

图8 不同速度下摩擦块的速度和位移时域曲线

以位移为横坐标，速度为纵坐标可以得到摩擦块不同速度下的运动相图如图9所示。从图9中可以看出，随着摩擦盘转速增加，摩擦块运动的极限环减小，即Stick-slip振动减弱，当速度达到8 rpm时，相图中没有明显的Stick和Slip阶段。摩擦块的运动相图进一步说明在同一个法向力下，摩擦盘的转速越大，Stick-slip振动越弱，当转速达到一定时，宏观的Stick-slip现象消失。

图9 不同转速条件下的摩擦块运动相图

4.2 不同转速下的静摩擦特性

进一步分析转速对Stribeck摩擦模型中静摩擦系数的影响规律。法向力为150 N，转速为2 rpm、4 rpm和6 rpm时系统出现了明显的Stick-slip振动，于是选取这3个工况进行摩擦系数的识别。对2 rpm、4 rpm和6 rpm三种转速条件下加载初始阶段的摩擦力和法向力时域信号进行分析，得到三种转速下的静摩擦系数分别为0.201、0.191和0.185，可以发现静摩擦系数呈现出随摩擦盘转速增大而减小的变化规律。

4.3 不同转速下的动摩擦系数及衰减系数

进一步分析法向力为150 N时不同转速条件下稳定阶段的动摩擦系数与相对速度的时域信号曲线，得到法向力为150 N时不同转速条件下Slip阶段动摩擦系数和相对运动速度的关系如图10所示。由图10可以看到，在速度较低时，摩擦系数都呈现出随速度增大而减小的负斜率现象，在相对速度接近0时，三种转速下的摩擦系数呈现出随转速增大而减小的变化规律。

进一步基于Stribeck摩擦模型的方程式(1)利用MATLAB对3组试验结果进行拟合，得到不同速度下Stribeck摩擦模型的衰减系数及Stribeck摩擦模型的摩擦系数曲线(图10中实线)。最终得到不同速度下Stribeck摩擦模型中3个参数如表2所示。由表2可知，随着摩擦盘转速增大，静摩擦系数和衰减系数逐渐减小，三种转速下动摩擦系数只发生了很小的改变。

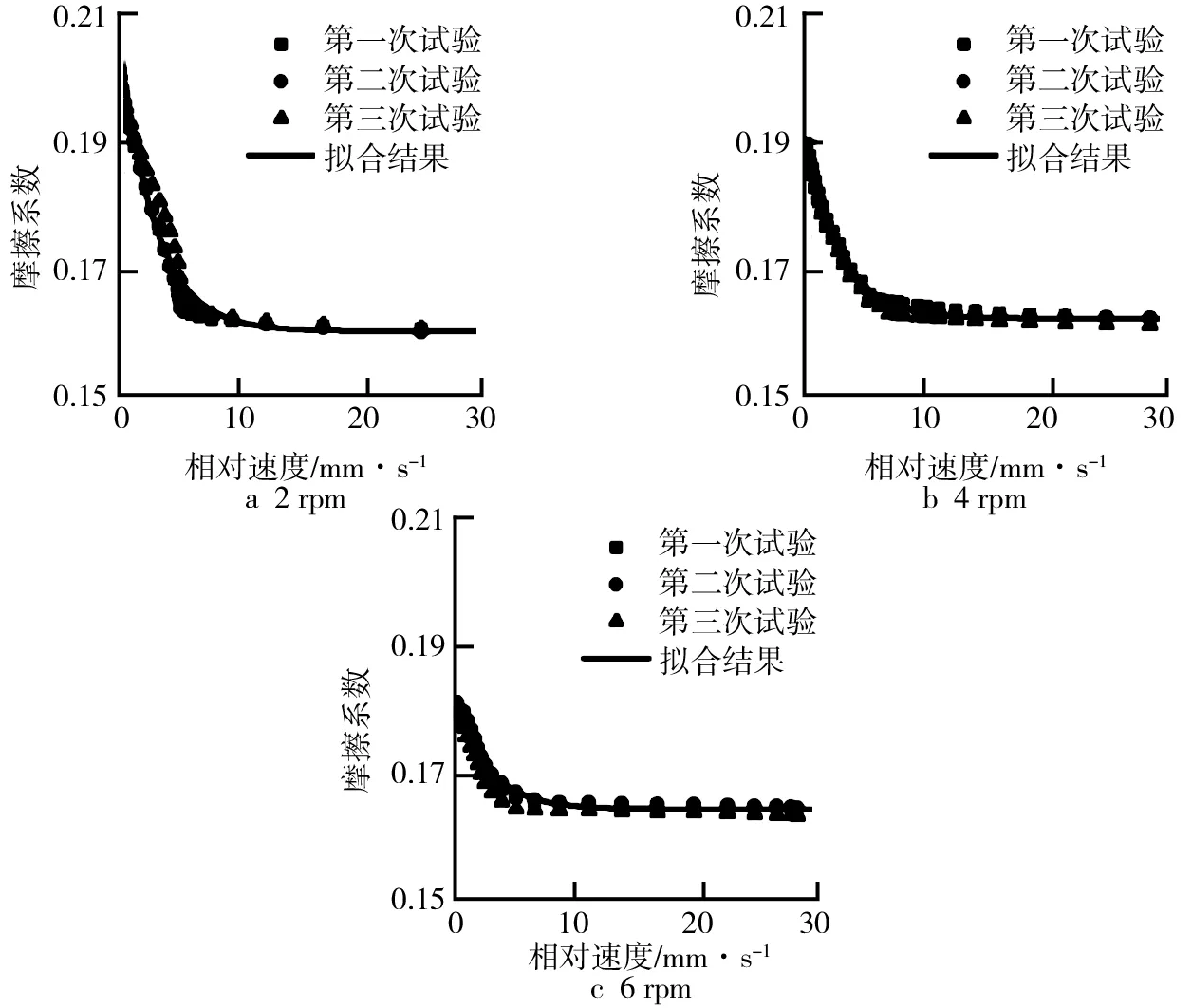
图10 不同转速下摩擦系数与相对运动速度的关系

表2 不同速度下Stribeck摩擦模型方程参数

5 结论

研究通过不同工况的Stick-slip振动试验，分析了法向力和摩擦盘转速对摩擦系统Stick-slip振动的影响，并基于试验结果辨识得到了Stribeck摩擦模型中的未知参数，分析了法向力和转速对Stribeck摩擦模型的动、静摩擦系数和衰减系数的影响。所得结论如下：试验结果表明法向力和摩擦盘的转速会影响摩擦系统的Stick-slip振动特性。法向力一定时，摩擦盘转速越大，Stick-slip振动越弱，当摩擦盘转速大于一定速度时，宏观的Stick-slip振动消失；摩擦盘转速一定时，在一定的范围内，法向力越大，Stick-slip振动越明显。动摩擦系数的值与相对运动速度有关，在试验条件下，相对速度低于5 mm/s时，呈现出摩擦系数随相对运动速度增大而减小的负斜率，相对速度增加到5 mm/s后，动摩擦系数几乎不再随相对运动速度变化。在同一个摩擦系统中，法向力的变化会影响Stribeck模型的动摩擦系数和衰减系数，法向力越大，动摩擦系数越大，衰减系数越小；转速的变化会影响静摩擦系数和衰减系数，转速越大，静摩擦系数和衰减系数越小，而对动摩擦系数影响很小。