模糊c均值聚类算法在员工绩效评价中的应用——以YH公司销售人员为例

张 翔，李国昌

(安徽建筑大学 经济管理学院，安徽 合肥 230031)

绩效评价方法对组织绩效的影响已经达到了显著性水平,员工的表现,如能力、知识、技能等同样对组织具有重要意义[1]。因此,人力资源管理的关键组成部分是能够让公司从员工中识别出优秀员工的评价技术。

以往的研究表明，绩效评价信息尤其适用于需要进行人际比较的决策(薪酬决定、晋升等)，需要进行个人比较的决策(反馈、个人教育需求等)，面向系统延续的决策(目标确定、人力规划等)和文件编制。显然，这些任务可以用传统的方法和工具来完成，然而，所有员工绩效评价方法对于所得评价数据的分析都采用加总排序的方式，这无疑在大量耗费企业人力、物力的同时，又忽略了各个指标的单独效应。因此，研究将模糊c均值聚类算法应用于评价数据的分析,以235名大型房地产公司销售人员年度评价数据为研究样本,采用FCM算法对数据进行软聚类。通过与传统方法评价结果进行比较,表明了该方法更好地利用了各个指标的单独效应,具有更高的灵活性和精准性,从而为完善现有绩效评价体系提供新的研究方向与思路。

1 理论分析

1.1 绩效评价

国外一些学者将绩效评价问题定义为一个没有为决策本身定义流程或规则的非结构化决策问题,以及一个典型的多标准决策(MCDM)问题,并经过研究表明,模糊性的应用可以成功解决此类问题[2]。近十几年来,国外学者基于模糊性的应用在指标的选择、评价体系的设计以及指标权重的赋予等方面的研究较为充分且透彻。Golec[3]等提出了一种利用模糊模型评价员工的综合层次体系。Kuo等运用模糊德尔菲法构建了服务业流动性的关键绩效评价指标。Secme等采用综合模糊层次分析法(FAHP)和优劣解距离法(TOPSIS)对银行绩效进行评价。Moon等采用模糊集合理论、电子名义群体技术和TOPSIS方法,通过多准则绩效评价流程对军事组织某一特定委员会候选人的筛选进行排序。Wu开发了一个用于员工绩效评估的集成模型,降低了第三方物流决策者的工作负荷。Özdaban等提出了一个模糊模型来确定工作和人员评价。Kelemenis等将模糊性应用于TOPSIS方法,进行人员选择的排名。Özdaban等利用模糊距离集对人员和工作进行联合评价。Sepehrirad[4]等构建了基于数学模型、德尔菲法、模糊层次分析法、简单相加加权法及TOPSIS方法对主观评价进行加权和汇总的360度绩效评价数学模型。Min-peng[5]等采用模糊综合评价和层次分析法对研发人员绩效考核进行建模。Gürbüz[6]等在绩效评价体系中加入了工程学的观点,开发了一种混合的多目标决策方法来评估员工在同一任务中的表现,并提出了同时处理定性和定量数据的有效方法。Özdemir[7]等在对土耳其大学绩效评价体系构建的过程中,运用模糊决策实验室法(Fuzzy DEMATEL)定量揭示了平衡计分卡的考察视角与指标之间的关系,然后利用该关系构造了模糊网络分析法(Fuzzy ANP)的网络结构并得到了各个视角和指标的权重。

相比较而言,国内学者则更加关注于评价视角、评价方法以及针对不同类型企业或团队的研究,对指标权重的确定仍是以德尔菲法及层次分析法为主。对于模糊性应用的相关研究主要集中在以模糊综合评价法为代表的评价指标确定方法。李锋[8]等结合功效系数法与模糊综合评价法,实行定性判断和定量分析的双重方式,建立了更加客观、精确、公正的营销绩效的考核模型。黄蓉蓉等针对物流企业绩效评价问题的复杂性和模糊性的特点,立足模糊综合评价法的观点,建立了包含3个一级指标和10个二级指标的基于模糊综合评价的物流绩效评价指标体系。魏洁等分析了研究型高校的教师绩效考核内涵和研究现状,基于模糊综合评价法确立了高校教师二级绩效评价体系。马强在新医改背景下,将模糊综合评价法用于公立医院绩效考核,架构了包括公益性、公众满意、服务质量、服务效率和服务能力在内的五大独特评价视角。陈都运用模糊综合评价法构建起我国高速铁路的模糊综合绩效评价模型,并以京沪高速铁路项目为例检验了该模型的先进性。

在深入研究了大量国内外相关文献后,可以确定平衡计分卡(BSC)、关键业绩指标法(KPI)、360°考核法及目标管理评价法(MBO)是实践中最常用的几种绩效评价方法。国内外学者近几十年的研究成果主要集中在考察视角综合性、评价方式科学性,以及运用模糊理论结合层次分析法(AHP)、网络层次分析法(ANP)、决策实验室法(DEMATEL)及TOPSIS等使得评价指标的选取具有更强的自适应性、指标权重的确定具有更高的精确性等方面。

然而,正如Espinilla[9]等所提出的,对于绩效评价数据的分析还没有确定的方法。这一问题并没有得到学者们的关注,现有方法仍是基于员工所得总分进行硬性分类。显然,累积的总分会导致每个指标的单独效应失效,因为总分相同的不同员工可能是有差别的,而对于数据的模糊聚类可以成功解决这一问题。国内学者成功将FCM算法应用于其他领域的评价与分类的相关研究愈发多见。郝杰[10]等基于FCM算法及粗糙集的云模型理论提出了用于岩爆等级评价的新模型,并以国内外40例岩爆工程为研究对象,运用基于FCM算法的粗糙度理论进行因子属性重要性评价,计算各评价因子权重。黄宝婵等针对乳腺肿瘤红外图像的识别,提出一种基于模糊C聚类的实现方法。徐珍珍等采用灰色关联度法和FCM算法相结合的模式识别模型进行木香质量多指标综合评价研究。

因此，研究将模糊c均值聚类算法应用于员工绩效评价数据的分析,通过克服传统加总排序的数据分析方式所带来的弊端,使员工绩效评价更加精准和有效。

1.2 模糊c均值聚类算法

聚类在模式识别、系统建模、图像处理、通信系统、数据挖掘、分类学、医学、地质学和商业等许多工程领域都发挥着重要的作用。聚类方法将一组N个输入向量分成c组,使同一组的成员彼此之间的相似性大于与其他组的成员之间的相似性。集群的数量可以预先定义,也可以通过其他方法确定(Tushir & Srivastava)。如果数据组能够很好地分离,那么硬聚类方法就是一个自然的解决方案,但如果聚类是重叠的,并且一些数据部分地属于多个集群,那么模糊聚类是处理这类情况的一种好方法。与传统的硬性聚类方案(如K均值聚类)不同,传统的硬性聚类方案将每个数据点分配给特定的集群,FCM算法则采用模糊划分,使得每个数据点在一定程度上属于一个由隶属度等级指定的集群[11-12]。FCM根据已知聚类数c、模糊度q、以及输入向量的初始隶属度值确定集群。集群的成员关系由相应的隶属度定义,集群由表示聚类中心的数值描述。FCM作为一种无监督聚类算法,在农业工程、天文、化学、地质、医学诊断、模式识别和图像处理等领域有着广泛的应用,其理论基础是Dunn首次提出的一种基于目标函数最小化的模糊聚类方法,Bezdek利用模糊隶属度的加权指数将目标函数最小化推广到FCM算法[13]。

在FCM算法输出的结果中,拥有相同总分的员工可以在不同的集群中,这意味着拥有相同总分的不同员工可能是有差别的。另外,FCM的主要优势之一就是不做硬性分类,最终的决定属于决策者,如果员工对两个集群的隶属度非常接近,决策者就可以进一步进行定性分析,并将该员工分配给另一个集群。最后,该方法具有更高的灵活性和精准性,计算速度较快且时间、经济成本较低。

FCM是基于式(1)中目标函数迭代最小化的迭代优化算法。

(1)

(2)

利用拉格朗日乘子法对式(1)求导，可以得出隶属函数式(3)和聚类中心式(4)的更新方程。

(3)

(4)

式中，n为数据对象的数量；c为集群的数量；ukj表示第j个数据对象对集群k的隶属度,定义为式(2)。xj表示第j个数据对象,表示式(4)中定义的集群K的中心,表示第j个数据点与第k个聚类中心间的欧几里德距离；参数q是决定划分结果模糊程度的隶属函数加权指数(如q=1表示硬聚类,q=∞表示完全模糊)。该参数会影响FCM的性能,一般建议取1.5～2.5之间的值[14]。因此，研究中q取2。

2 研究方法

2.1 研究样本

研究的样本界定为企业员工,并以大型房地产企业YH公司216名销售人员2018年度绩效评价数据为主要研究对象,如表1所示。

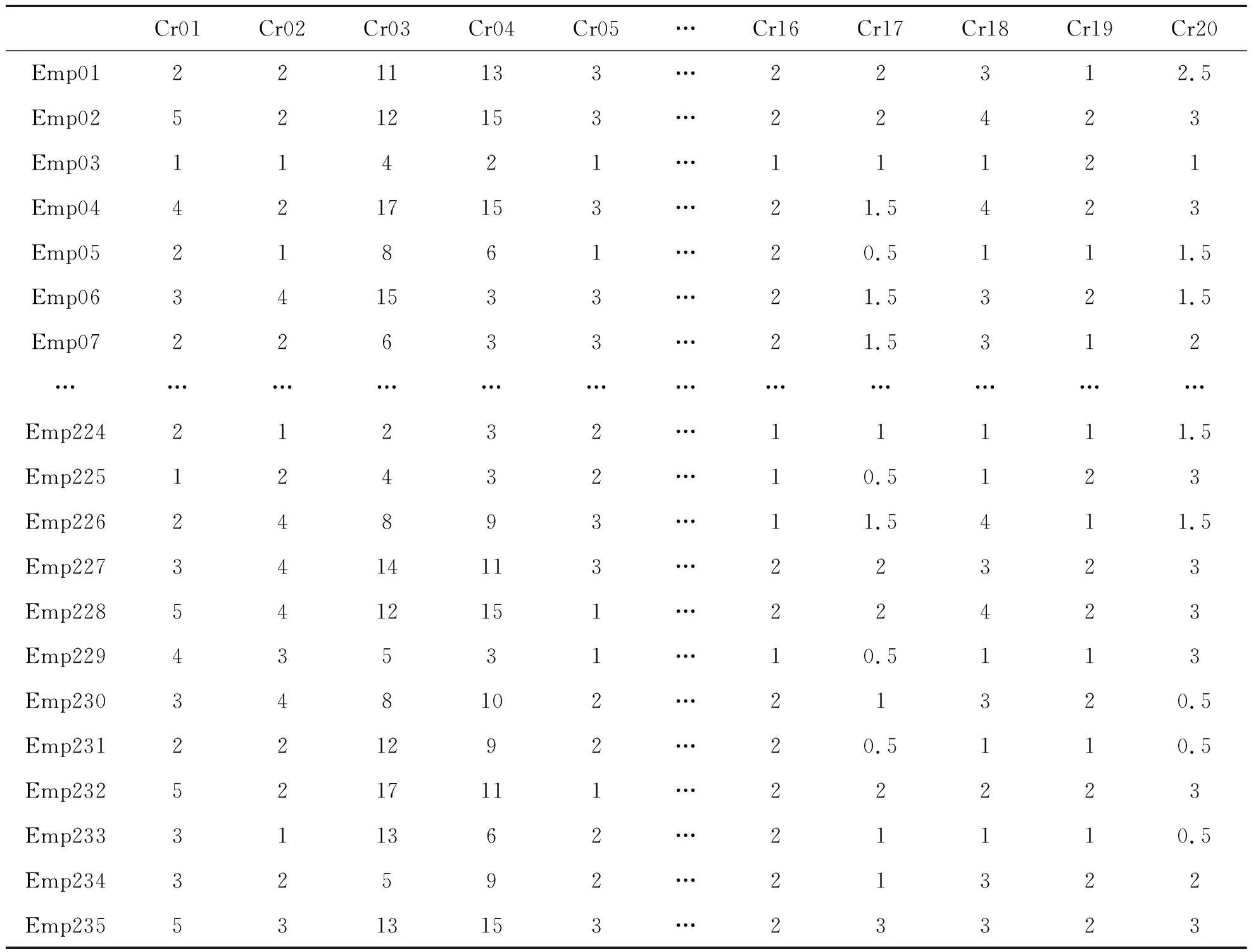
表1 YH公司销售部门季度绩效考核得分数据(基于各指标权重数值)

注:Emp表示员工编号,Cr表示关键指标编号

YH公司是BW集团的分公司,BW集团是中国十大房地产企业之一,也是中国领先的现代化大型房地产综合开发企业,专业从事房地产开发与经营管理。该公司销售部门目前采用的是结合平衡记分卡理论及关键绩效指标法，基于财务、客户、内部业务、学习发展四大维度所构建的包含20个关键指标的绩效评价体系,如表2所示。

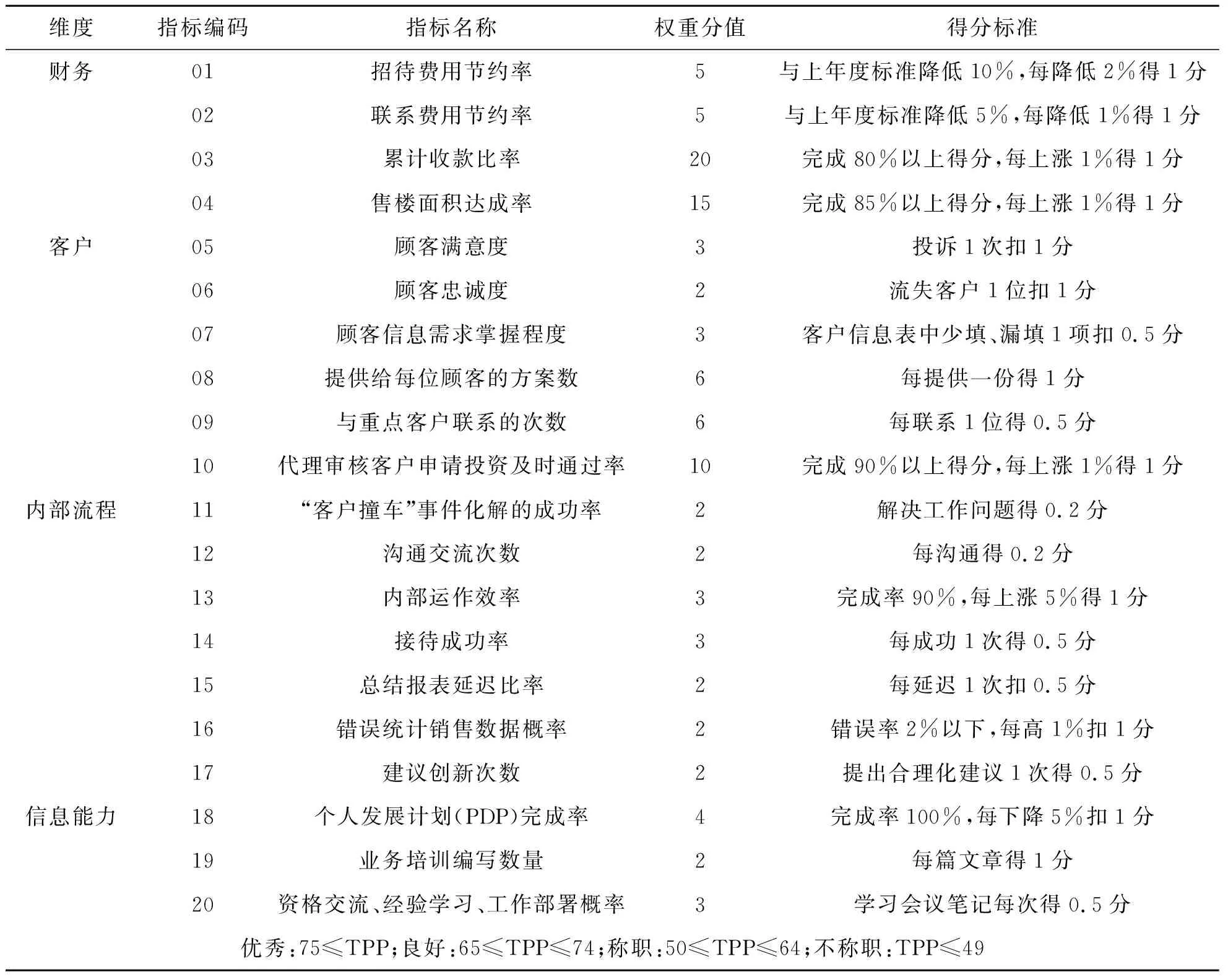
表2 YH销售人员考核体系

注:TPP表示各指标权重分值总和

2.2 分析技术

通过MATLAB 2018b以及下述FCM算法对YH公司39名销售人员2019年第一季度(1～3月)绩效评价数据进行聚类,计算每个员工关于所有集群的隶属度,每个集群表示不同的绩效等级,而后根据聚类中心按降序定义集群,最后将输出结果与传统加总方式比较,分析FCM算法是如何解决绩效评价数据分析问题的。

FCM算法步骤：

输入：要集群的数据对象、集群数量c、阈值(error_rate)和最大迭代次数(max_iteration)

(1)初始化隶属矩阵(k=1,2,…,c;j=1,2,…,n)

(2)Fort=1,2,3,…,max_iteration

①使用式(4)更新集群中心。

③使用式(1)新目标函数。

④If (‖Jq(u,V,X)new-Jq(u,V,X)old‖≤error_rate则算法停止。

输出：最终的集群数据。

FCM参数设置：

集群数量c=4(便于将FCM与公司现有绩效分级进行比较),聚类误差=0.01

error_rate=2，max_iteration=100。

3 研究结果

3.1 各员工对4个集群的隶属度

FCM算法按照输入参数构建4个绩效集群,为每个员工计算这些集群的隶属度,并采用员工的最高隶属度确定每个员工隶属的集群，如表3所示。由表3结果可知,每个员工都被附加到最合适的集群。例如,Emp01附属于隶属度为0.349 961 06的集群2,Emp03附属于隶属度为0.682 469 072的集群4。

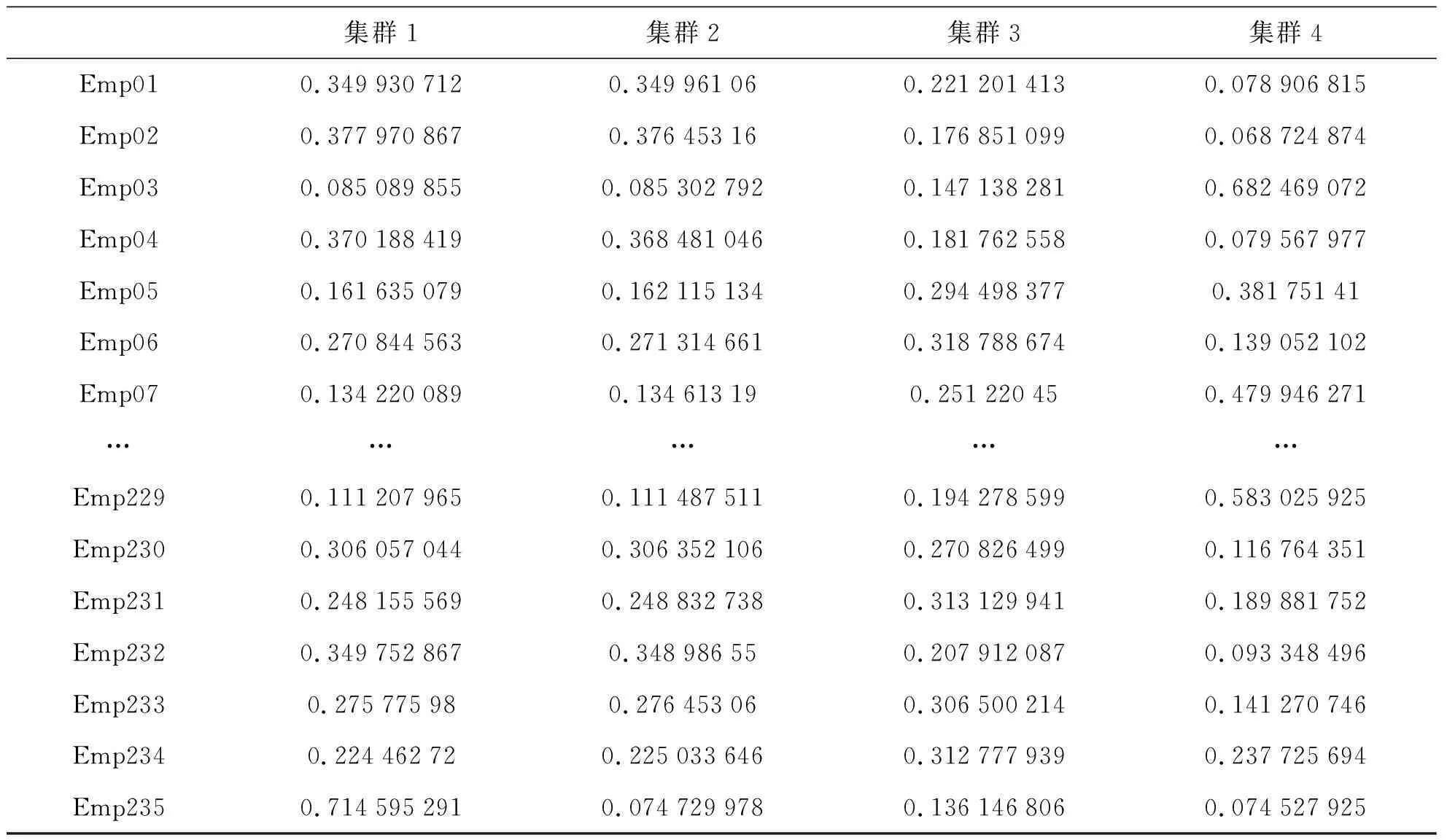
表3 员工对各集群的隶属度

3.2 聚类中心及绩效分级

在机器学习方法中,集群由其聚类中心有效地表示,算法完成后,构建聚类、计算聚类中心、标记聚类，如表4所示,将聚类中心按照降序排列以实现绩效的分级。

表4 基于FCM算法的绩效分级

FCM算法将员工02，04，15，17，…，211，218，220，231，233，235聚类为集群1,其绩效评价级别最高(4.346 104 498),由公司授予优秀员工。在日后的工作中,公司应当鼓励和激励集群2的员工向集群1迈进。在集群3中,公司应当分析员工的不足并进行相应的培训。FCM算法将第03，05，07，08，11，…，223，224，228，230和第232名员工聚类为集群4,他们属于许多指标有所欠缺的类别,这个中心值最小的集群(2.080 014 87)包含了235名员工中最需要自我反省的员工。

人力资源部门在审查这些集群时,应该详细审查成员的隶属度。例如在集群4中,第132名员工的隶属度为0.714 343 869;第145名员工的隶属度为0.714 595 291;第232名员工的隶属度为0.682 469 072。在这3名员工中,第232名员工的绩效水平高于另外两名员工,第145名员工表现最差。在这种情况下,如果公司想解雇一名员工,应当在这3名员工中选择第145名员工。同样,如果公司想奖励一名员工,则应该选择集群1的第32名隶属度为0.384 256 638的员工。

3.3 基于加总方法和FCM算法的绩效分级比较

基于加总方法和FCM算法的39名员工绩效分级比较如表5所示。由表5可知，第06、22、57、73、92、…、221名员工分别为66.9分、67分、67.2分、67.3分、67.7分、…、68.2分,属于等级2,但是根据FCM结果,该员工属于等级3。同样,第173名员工属于等级2,但FCM将该员工划分为优秀员工。另外,虽然第178名和第221名员工具有相同的TPP值(68.2),但FCM将他们分配到不同的绩效等级，类似的分配还有第71名和第149名员工等。简而言之,传统方法将部分员工与FCM进行了不同的分类。这些差异是传统的加总方法以固定分数为界限进行硬性分类以及累积的总分导致20个指标的单独效应的损失所带来的弊端。

表5 基于加总方法和FCM算法的39名员工绩效分级比较

4 结论

绩效评价数据的分析尚未有确定的方法,实践中采用加总的方式处理会导致每个指标的单独效应失效,因此,研究提出了一种FCM算法来替代传统的评价数据分析方法,并取得成功。研究方法在弥补传统方法的不足方面做出了重要而显著的贡献,简要总结如下:FCM算法解决了总分累积所导致的单指标效应失效问题；FCM算法不需要制定硬性分级标准,根据各指标评价数据自动进行更为科学的软聚类；FCM算法分级数目可以根据实际需要做出调整,输出结果也更为多样,比加总方法更为灵活；FCM算法可以将总分相同的员工划分到不同的绩效等级中,较之加总方法更为精确；最后，FCM算法计算速度极快,极大地节约了评价数据分析的时间、经济成本。