磁极错位削弱永磁直线伺服电动机齿槽法向力波动方法
夏加宽 沈 丽 彭 兵 宋德贤
(沈阳工业大学电气工程学院 沈阳 110870)
磁极错位削弱永磁直线伺服电动机齿槽法向力波动方法
夏加宽沈丽彭兵宋德贤
(沈阳工业大学电气工程学院沈阳110870)
单边平板式永磁直线伺服电动机(PMLSM)在运行过程中动、定子之间存在较大的法向力波动,法向力波动引起的摩擦力摄动和机床振动极大地影响了机床的加工精度,齿槽效应是引起永磁直线伺服电动机法向力波动的一个重要原因。为此,采用麦克斯韦张量法推导了动子边齿无限长无端部效应的PMLSM法向电磁力的解析表达式,揭示齿槽效应引起的法向力波动的规律。通过对傅里叶分解系数的分析,得出齿槽效应产生的法向力波动的主要谐波次数,提出永磁磁极三段错位法以削弱其引起的主要谐波法向力波动,消除传统的斜极、移相优化方法产生的电动机横向俯仰运动。最后以齿槽法向力波动较为明显的12槽8极PMLSM为例,采用有限元仿真和实验验证,结果证明该方法不仅能够削弱齿槽效应产生的法向力波动,还能在推力基本保持不变的情况下,有效地削弱推力波动。
永磁直线伺服电动机齿槽效应法向力波动磁极三段错位法
0 引言
永磁直线伺服电动机以其推力大、加速度高、实现直线进给系统“零传动”等优点,成为高精、高速数控机床的重要功能部件[1,2],广泛应用于高精密光学加工与检测等领域[3,4]。平板型永磁直线伺服电动机的动、定子之间存在较大的法向电磁力,同时,由于存在齿槽效应、端部效应和磁动势谐波等,在电动机运行过程中,还存在法向力的波动。法向力波动一方面以摩擦力扰动的形式影响水平推力性能[5,6];另一方面会引起机床的振动,是影响精密机床加工精度的重要因素。
对于永磁直线伺服电动机的法向力及其波动的分析及抑制方法近年来已经引起学者的注意。文献[7]对永磁直线电动机初级与次级间的法向吸力进行了详细的分析,认为法向电磁吸力主要是由于次级永磁体的强磁场引起的,初级电枢电流对其影响较小,法向电磁力波动是极距的周期函数。文献[8]分析研究了无槽永磁直线同步电动机推力和法向力分布,给出了解析公式,得出了法向力与位置的变化关系。文献[9]在分析基波气隙磁场分布基础上,利用麦克斯韦张量法推导了法向电磁力的解析方程,研究了极槽配合以及气隙长度对法向力的影响。文献[10,11]借助有限元软件研究了永磁直线电动机的法向力及其波动,借助削弱直线电动机推力波动的方法,分别通过改变端齿结构和磁极形状来削弱法向力波动。文献[12]采用数值法分析法向力的波动幅值对机床结构变形及机床振动的影响,并采取机械设计方案进行优化。文献[13]评估了法向力对平板型永磁直线电动机的性能影响,基于磁场分布和麦克斯韦张量法研究了平板型永磁直线电动机法向力的特征,但未对其波动规律进行分析。综上所述,气隙磁场是影响法向力的主要原因,电枢铁心开齿槽引起的气隙磁导波是引起法向力波动的重要因素。但还欠缺揭示齿槽效应引起的法向力波动规律的解析分析,以及针对波动规律的有效削弱方法。
齿槽是影响法向力波动的一个重要原因,本文以平板表贴式动铁型永磁直线伺服电动机为研究对象,首先利用麦克斯韦张量法和积分法推导齿槽效应产生的永磁直线电动机动子的法向力波动解析表达式,分析其主要谐波次数;然后从相位补偿角度分析永磁磁极三段错位法削弱法向力波动的原理;最后以12槽8极永磁直线伺服电动机为例,分别采用有限元仿真和实验验证该方法的有效性。
1 永磁直线伺服电动机空载齿槽法向力波动解析
永磁直线伺服电动机在电枢绕组开路时,动子受到切向推力和法向吸力的双重作用。文献[14]将齿槽和端部效应引起的切向推力称为磁阻力(detent force),而对其引起的法向电磁吸力波动还未命名,本文研究齿槽效应引起的法向力波动,这里简称齿槽法向力波动。空载时齿槽法向力波动是永磁磁动势与气隙磁导相互作用的结果,基于磁动势和磁导波的永磁直线伺服电动机的物理模型如图1所示。

图1 永磁直线电动机物理模型及磁感应强度和磁导波Fig.1 Physical model of PMLM,magnetic flux density and permeance wave
图1中,l为电枢铁心长度;lFe为电枢铁心宽度;bt为有效齿顶宽度;δ为气隙长度;t1为槽距;μ0为真空磁导率;z为电动机槽数;p为正对电枢铁心长度l下的电动机极数;hPM为永磁体高度;τm为永磁体宽度;τ为极距;αp为极弧系数,αp=τm/τ;λ(x,y)为相对气隙磁导;Br为永磁体剩余磁感应强度最大值;x为以某一指定齿中心线为原点的位置函数;y为某一指定齿中心线与某一对极中心线的距离。
1.1法向力的解析分析方法
为便于分析,作如下假设:①电枢铁心磁导率μFe为无穷大,不计饱和磁压降,磁力线不经过槽部;②永磁体的磁导率与空气的相同;③永磁体的磁力线垂直进入动子铁心,即只有法向磁场,而无切向磁场;④动子为无限长,即不考虑端部效应。
根据磁路基尔霍夫第二定律可得到永磁磁极在气隙中产生的磁场为永磁磁动势与相对气隙磁导的乘积

式中,HPM为永磁体磁场强度;λ(x,y)=μ0/δ。
电枢绕组开路时,动子受到的法向力就是永磁磁极对定子铁心的吸引力。由麦克斯韦张力张量定理可知,动子铁心单位面积的法向力为

将式(1)代入式(2),可得动子铁心单位面积受到的法向力为

对动子铁心面积积分,可得直线电动机动子受到的法向力为

1.2法向力波动的谐波分析



式中,
将式(5)、式(6)代入式(4)得

式中,v为电动机运行过一对极的法向力谐波次数,v=2kzτ/l。
从式(7)可以看出,当动子和定子相对位置固定时,动子和定子之间只存在恒定的法向力,随着动子和定子间的相对位移y发生变化,法向力也就产生了波动分量。不是和λ2(x,y)所有的傅里叶分解系数都对法向力波动有影响,只有满足条件kz=np的傅里叶系数才对法向力波动产生作用。根据式(7)可列出齿槽效应对部分极槽配合电动机产生的主要的法向力波动谐波次数,见表1。其中把齿槽法向力波动的最低次数称为齿槽法向力的基波,用v1表示,高次的齿槽法向力波动次数均是基波的整数倍,可表示为mv1(m=1,2,3,…)。

表1 不同极槽配合电动机的法向力波动次数Tab.1 The orders of normal force ripple with differences in pole-slot combinations
2 永磁磁极三段错位法削弱齿槽法向力波动
根据式(7)和表1可知,对于某一固定极槽组合的永磁直线伺服电动机,齿槽法向力波动主要谐波次数及相位关系是固定的。将式(7)的恒定部分去掉,得出电动机动子受到的v次齿槽法向力表达式为

如果将每个磁极沿X轴方向等分为两段,错开Δy距离,第一段磁极与齿槽产生的v次法向力的表达式如式(8),用y+Δy代替式(8)中的y得出第二段磁极与齿槽产生的v次法向力表达式为

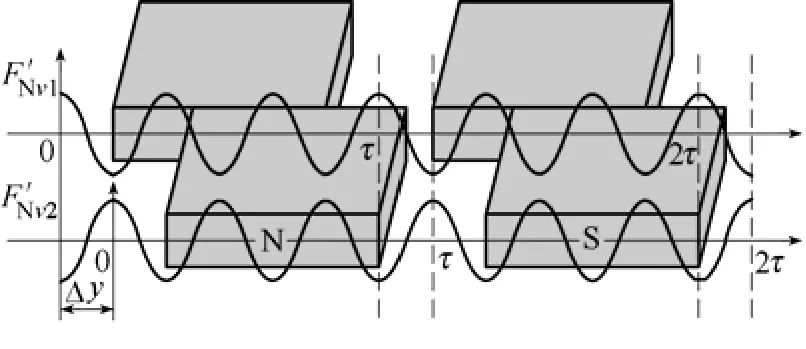
图2 永磁磁极两段错位法原理Fig.2 Schematic of two sections of permanent magnet staggered method
这种永磁磁极两段错位法,使得电动机动子沿横向受到的法向力不均等,从而引起电动机横向俯仰运动。基于此,提出永磁磁极三段错位法,将电动机永磁磁极沿X轴分成三段,中间段磁极长度是两侧段磁极长度的两倍,图3为采用永磁磁极三段错位法的12槽8极PMLSM的三维模型及原理图。

图3 永磁磁极三段错位法Fig.3 Three sections of permanent magnet staggered method
由于其磁极沿Z轴的对称分布,永磁磁极三段错位法能够在不发生电动机横向俯仰运动的情况下,消除v次齿槽法向力,进而削弱齿槽法向力波动。
3 仿真结果与分析
3.1永磁磁极三段错位法削弱齿槽法向力波动的仿真分析
为验证永磁磁极三段错位法削弱齿槽法向力波动的有效性与正确性,本文以齿槽法向力波动较为显著的12槽8极开口槽永磁直线电动机为例,由于端部效应也是引起永磁直线电动机法向力波动的一个重要原因,为了消除端部效应的影响,有限元建模时,动子边齿的长度为无限长,而定子为有限长,电动机参数见表2,电动机模型如图4所示。

表2 电动机参数Tab. 2 Motor parameters

图4 动子无限长电动机模型Fig.4 Model of the motor with infinitely long mover
12槽8极电动机极距为22mm,法向力波动的主要谐波次数为6次。根据式(9)求出磁极相对位移应为Δy=3.667mm。采用永磁磁极三段错位法前后的法向力及法向力波动频谱如图5所示。
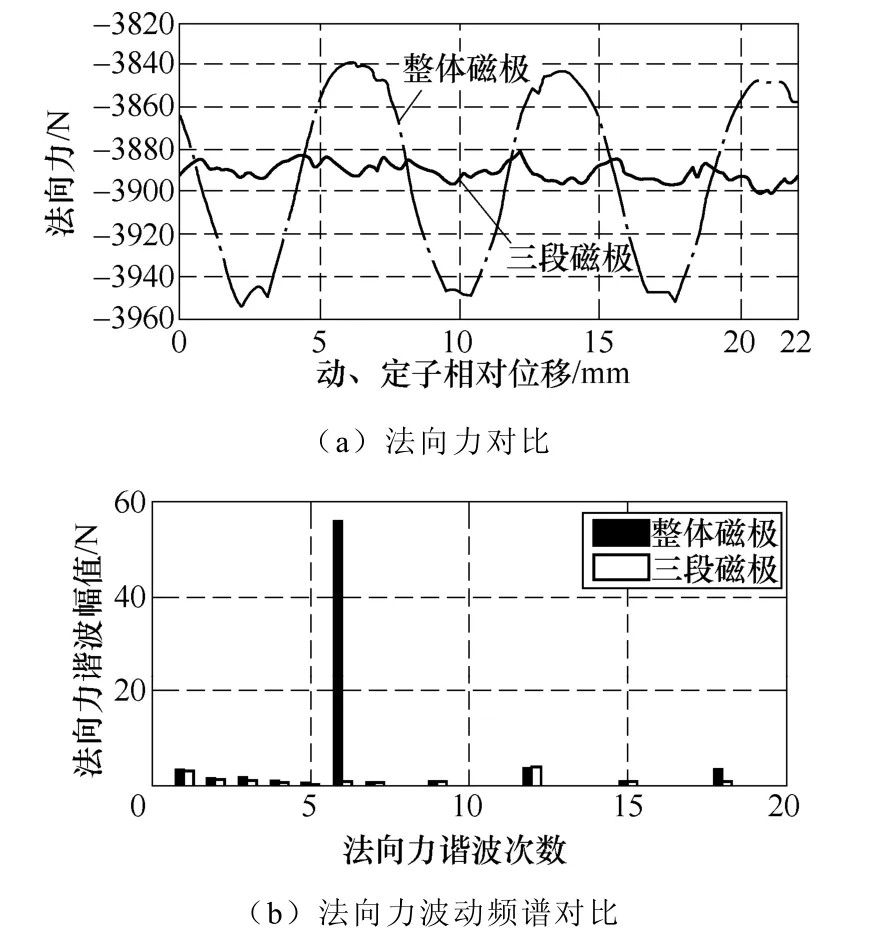
图5 法向力仿真结果Fig.5 Simulation results of the normal force
由图5可知,采用永磁磁极三段错位法前齿槽法向力波动的基波次数为6次,这与1.3节的解析分析结果一致。采用永磁磁极三段错位法后,对于基波的奇数倍次谐波,6次谐波幅值由56.5N减小到0.4N,18次谐波幅值由4.0N减小到0.6N,基本被抵消;对于基波的偶数倍次12次谐波,当磁极相对位移Δy=3.667mm时,两部分磁极与齿槽产生的法向力的相位相差2π,12次谐波幅值由4.6N增加到5.0N,变化较小。这与第2节分析结果一致。总的法向力波动峰峰值由103.9N减小到29.5N,有限元仿真结果证明永磁磁极三段错位法能够有效地减小甚至抵消齿槽法向力波动基波的奇数倍次谐波,进而削弱齿槽法向力波动。
3.2永磁磁极三段错位法对推力影响的仿真分析
推力性能是永磁直线伺服电动机的重要指标,在削弱法向力波动的同时,不应对电动机推力性能有较大影响。图6是采用永磁磁极三段错位法前后空载和负载时的推力及其波动。

图6 推力仿真结果Fig.6 Simulation results of the thrust
由图6a可知,空载时,采用永磁磁极三段错位法前后齿槽引起的推力波动由102N减小到18N;由图6b可知,负载时采用id=0、iq=7A供电,采用永磁磁极三段错位法前后齿槽推力波动由65N减小到22N,平均推力由290N减小到274N,衰减5.6%。仿真结果证明,采用永磁磁极三段错位法能够在推力衰减较小的情况下,有效地削弱电动机的法向力波动和推力波动。
4 实验结果与分析
永磁直线伺服电动机法向力波动静态测试系统由进给装置及检测单元组成,其中检测单元包括光栅尺与数显表、四个FC-WM微型拉力传感器及安装装置与变送器、BVM-300-4M四通道拉力测试仪与模态分析软件。利用辅助安装装置将4个拉力传感器安装在工作台和电动机动子之间,如图7所示,并调节预紧力;当电动机动子在导轨上移动时,由光栅尺和数显表测量动子和定子的相对位移,由拉力测试仪采集四个拉力传感器数据,间接计算电动机动子在一个极距范围内受到的法向力。图8为采用永磁磁极三段错位法前后实验结果与有限元仿真结果的对比。

图7 法向力静态测试系统Fig.7 Static measurement system of the normal force

图8 法向力静态测试结果Fig.8 Static measurement results of the normal force
由图8可知,采用永磁磁极三段错位法前后法向力测量结果与有限元仿真结果基本符合,法向力波动被有效地削弱。实验结果与仿真结果存在一定的偏差的主要原因有:①这种加装动子加长板的样机只是近似消除动子端部效应,不能消除定子轭部的端部效应;②永磁体充磁不均,采用三段式结构在安装上存在一定误差;③电动机制造以及安装上存在一定形位误差,检测单元误差等;④仿真时没有考虑磁极错位后两磁极所形成的直角处产生的磁耦合带来的影响。
5 结论
永磁直线伺服电动机齿槽法向力波动是永磁磁动势与铁心作用的结果。通过解析分析,揭示了永磁磁场谐波和气隙磁导谐波对法向力波动的影响规律,得出PMLSM法向力波动的解析表达式;通过对解析式的傅里叶系数分解得出,只有kz=np次傅里叶分解次数才对法向力波动产生作用,从而可确定法向力波动的主要谐波次数;提出的永磁磁极三段错位法可削弱甚至抵消主要次谐波,从而削弱齿槽法向力波动。有限元仿真和实验结果验证了该方法的有效性。
[1] Baatar N,Yoon H S,Pham M T. Shape optimal design of a 9-pole 10-slot PMLSM for detent force reduction using adaptive response surface method[J]. IEEE Transactions on Magnetics,2009,45(10): 4562-4565.
[2] 董婷,黄伟,王成元. 不等齿顶宽间隔绕组对直接驱动转台电机转矩特性的影响[J]. 电工技术学报,2010,25(8): 12-17.
Dong Ting,Huang Wei,Wang Chengyuan. Influence of unequal teeth tips width and alternate winding on torque characteristics in direct drive table motor[J]. Transactions of China Electrotechnical Society,2010,25(8): 12-17.
[3] 彭兵,夏加宽,王成元,等. 近极槽数表贴式永磁同步电动机齿顶漏磁分析与计算[J]. 电工技术学报,2012,27(1): 114-118.
Peng Bing,Xia Jiakuan,Wang Chengyuan,et al. Analysis and calculation of zigzag leakage flux in surface-mounted pm synchronous machines with similar number of poles and slots[J]. Transactions of China Electrotechnical Society,2012,27(1): 118-114.
[4] Li Hong,Zhou Yunfei,Shi Yangchun. Motion control for wafer stage of 0.1μm lithography[C]. IEEE International Conference on Integration Technology,2007: 338-342.
[5] 夏加宽,赵鹏,黄伟. 直线伺服电机法向力分析[J].电气开关,2010 (4): 15-17.
Xia Jiakuan,Zhao Peng,Huang Wei. Study on the normal force of a linear servo motor[J]. Electric Switchgear,2010(4): 15-17.
[6] 陆华才,江明,郭兴众,等. 永磁直线同步电机推力波动约束[J]. 电工技术学报,2012,27(3): 128-132.
Lu Huacai,Jiang Ming,Guo Xingzhong,et al. Thrust ripple suppression for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society,2012,27(3): 128-132.
[7] 郭瑶瑶,刘成颖,王先逵. 机床进给系统用永磁直线电机法向吸力的研究[J]. 中国机械工程,2007,18(10): 1174-1177.
Guo Yaoyao,Liu Chengying,Wang Xiankui. Study on normal force in permanent magnet linearmotor in machine tool feeding system[J]. China Mechanical Engineering,2007,18(10): 1174-1177.
[8] Filho A F F,Da Silveira M A,Homrich R P. An analytical solution for the normal force in linear actuators[C]. IEEE International Conference on Electric Machines and Drives,2005: 1249-1254.
[9] 刘恒坤,张晓,弥柱. 空心和Halbach永磁直线同步电机的牵引力和法向力分析[J]. 国防科技大学学报,2012,34(3): 94-97.
Liu Hengkun,Zhang Xiao,Mi Zhu. Analytical computation of normal and tangential forces in linear synchronous motor with air-core and Halbach permanent magnets[J]. Journal of National University of Defense Technology,2012,34(3): 94-97.
[10] Xia Jiakuan,Li Weiyang,Li Shen. Skew and end-teeth optimization in reduce permanent magnet linear synchronous motor normal force fluctuation[J]. Advanced Materials Research,2011,383-390: 4853-4859.
[11] Huang Rui,Zhou Jianpei,Kim G T. Minimization design of normal force in synchronous permanent magnet planar motor with halbach array[J]. IEEE Transactions on Magnetics,2008,44(6): 1526-1529.
[12] 宁建荣,夏加宽,沈丽,等. 基于拓扑优化的高精机床直线进给系统减振设计[J]. 组合机床与自动化加工技术,2012(12): 45-48.
Ning Jianrong,Xia Jiakuan,Shen Li,et al. Design of[13] Chen Yan, Jin Jianxun, Zheng Luhai. Normal force and the parameters of permanent magnet linear synchronous motors[C].International Conference on Applied Superconductivity and Electromagnetic Devices, 2011: 239-242.
reduce vibration for linear feed system of high precision machine tool based on topology optimization[J]. Machine Tool & Automatic Manufacturing Technique, 2012(12): 45-48.
[14] 潘开林, 傅建中, 陈子辰. 永磁直线同步电机的磁阻力分析及其最小化研究[J]. 中国电机工程学报, 2004, 24(4): 112-115.
Pan Kailin, Fu Jianzhong, Chen Zichen. Detent force analysis and reduction of PMLSM[J]. Proceedings of the CSEE, 2004, 24(4): 112-115.
The Magnet-Staggered Method to Weaken the Cogging Effect Normal Force Ripple of Permanent Magnet Linear Servo Motor
Xia JiakuanShen LiPeng BingSong Dexian
(Shenyang University of TechnologyShenyang110870China)
There is the large normal force ripple between the mover and stator when the single-side flat-plate permanent magnet linear servo motor (PMLM) is operating,and the friction force perturbation and the vibration of the machine tool caused by the normal force ripple will influence the accuracy of machine tool greatly. The cogging effect of PMLM is one of the important factors that cause the normal force ripple. Therefore,the normal force analytic expression of the infinitely long side tooth PMLSM which is derived with the Maxwell tensor method,which reveals the law of the normal force fluctuation caused by cogging effect. The primary harmonic of normal force caused by cogging effect is obtained by Fourier decomposition method,and the three sections of magnets staggered method to weaken the normal force ripple is presented to remove the lateral movement of the motor in traditional skewed pole and phase shift optimization methods. In the end,take 12 slots 8 poles PMLSM with obvious cogging normal force ripple for example,the finite element simulation and experiment methods are employed in this paper,and the results show that the method can reduce the cogging effect effectively without changing the thrust of PMLSM.
Permanent magnet linear servo motor,cogging effect,normal force ripple,three sections of magnets staggered method
TM351
夏加宽男,1962年生,教授,博士生导师,主要从事永磁伺服电动机设计与控制。
沈丽女,1981年生,博士研究生,主要从事永磁直线伺服电动机的设计与控制。
国家自然科学基金(51377108),辽宁省高等学校创新团队(LT2013006)和国家科技重大专项子课题(2012ZX04001-011-003)资助项目。
2013-12-24改稿日期 2014-03-24

