十字形多自由度超声电机接触分析模型研究*
□ 刘 扬 □ 张健滔
1.上海大学 机电工程与自动化学院 上海 200072
2.上海大学 上海市智能制造及机器人重点实验室 上海 200072
十字形多自由度超声电机接触分析模型研究*
□ 刘 扬1,2□ 张健滔1,2
1.上海大学 机电工程与自动化学院 上海 200072
2.上海大学 上海市智能制造及机器人重点实验室 上海 200072
十字形多自由度超声电机其动子绕X、Y轴旋转与绕 Z轴旋转的驱动机理是不同的,根据弹性接触理论,对其进行了分别考虑,并建立了电机摩擦接触分析模型。利用建立的模型,对多自由度电机机械特性进行了估算,分析了定子振幅、摩擦因数、驱动频率对电机输出性能的影响规律。对所研制样机的机械特性进行了测试,结果表明,所建立的模型对十字形超声电机特性的预估是有效的,可为多自由度超声电机设计提供指导。
多自由度超声电机 接触模型 仿真分析 机械特性
随着机电系统的发展,使用多自由度驱动的场合越来越多,例如多自由度运动平台、机器人关节与眼球驱动等,这些应用对驱动器提出了体积小、功率密度大、定位精度高等要求。传统的多个单自由度电机驱动,存在结构复杂、体积大、质量重等问题。因而对多自由度电机的研究十分必要,特别是多自由度超声电机,由于其具有结构简单、直接驱动、推重比大、惯性小、响应快、断电自锁、可控制性好和定位精度高等优点,备受国内外学者的关注[1-5]。
建立多自由度超声电机定、动子接触模型,有助于理解其运行机理,了解各参数对机械特性的影响,可为电机设计提供指导。目前研究较多的是行波型多自由度超声电机的理论模型,最早,Takashi Maeno[6]利用有限元方法建立了行波型单自由度超声电机模型。Joachim[7]通过假设定子为伯努利-欧拉梁,建立了行波单自由度超声电机定、动子接触模型。国内学者也对行波单自由度超声电机的定、动子接触模型进行了深入研究,周盛强等利用有限元三维点点接触单元,分析了接触界面的接触状态,曲建俊等假设定子摩擦层为黏弹性体,提出了行波超声电机黏弹性接触模型[4-5,8-9]。这些学者深入研究了行波单自由度超声电机接触模型,但有关多自由度超声电机接触模型的研究很少有报道。笔者对所研制的一款十字形多自由度超声电机的定、动子接触机理进行了研究,并建立其理论接触模型,利用该模型进行电机机械特性仿真。
1 十字形多自由度超声电机接触模型
1.1 十字形多自由度超声电机结构
研制的一款十字形多自由度超声电机结构如图1所示,电机动子为球形金属体,定子整体结构呈十字
形,定子中心开方形盲孔,将定子分为后驱动足、右驱动足、前驱动足、左驱动足,4片压电陶瓷非对称地贴在定子的4个驱动足上。动子直径大于定子中心方形盲孔的宽度,定子与动子沿竖直方向具有一定的接触压力,并通过摩擦传动。该超声电机可实现绕X、Y、Z轴旋转,具有结构紧凑、构件少、易于小型化等特点。
十字形多自由度超声电机利用两个振动模态工作,如图2所示。第一振动模态的振型如图2(a)所示,其左右驱动足交替伸长、收缩。第二振动模态的振型如图2(b)所示,其前后驱动足交替伸长、收缩,两个工作振动模态的频率需近似相等。

▲图1 十字形多自由度超声电机样机

▲图2 电机工作模态振型
1.2 绕X、Y轴旋转时的定、动子接触模型
电机定子驱动动子绕X、Y轴旋转时,工作机理类似,只需激励出其中一个工作模态。以绕X轴旋转为例进行分析,此时只需激励出工作模态一。电机正常工作时,定子驱动足与动子接触点作斜线运动。定子工作时驱动质点P的位移响应为:

当电机稳态工作时,定、动子间接触状态如图3所示。式(1)表示定子工作时驱动质点P位移响应可转换到NOτ坐标系,如图3(a)所示,即:
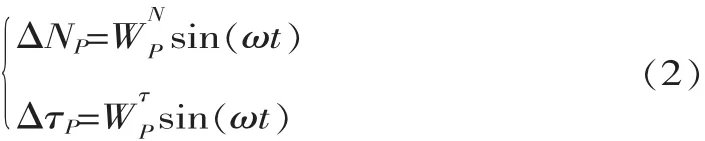
在一个驱动周期内,驱动质点与动子的状态分为:接触期和脱离期。当定子、动子稳定工作后,驱动质点P沿法向N的位移如图3(b)所示,σ0表示定子稳态工作时驱动质点的法向平衡位置面到动子接触表面的距离。
在驱动质点与动子脱离时,动子沿N方向的接触变形量δN(t)=0;接触时,可表示为:

式中:WC为定子、动子接触状态下定子驱动点的振幅。
设ta、td分别为驱动足与动子开始接触及开始脱离时间,一个驱动周期内定子与动子接触时间为:

设ε=Tj/T,T为驱动周期,所以有:

在驱动足与动子接触时段内,定子驱动质点的法向和切向位移及速度都是变化的。为简化分析,由于电机稳态工作时定、动子间接触频率很高,且动子有一定惯性,可假定动子在稳态工作时速度不变为vs1。驱动足与动子接触区域内,定子驱动足上质点切向振动速度vτ不断变化,故在接触时段内存在等速点(即定子驱动点切向振动速度与动子切向速度相同的点),如图4所示。
根据库仑定律,驱动足与动子间的摩擦力为:
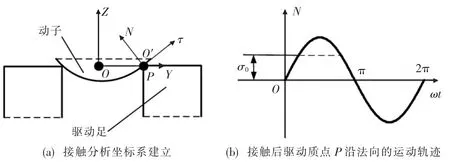
▲图3 驱动足与动子接触状态示意图

▲图4 一个周期内定、动子切向速度关系及做功示意图

式中:μd为驱动足与动子间动摩擦因数。
根据动量定理,一个周期内定子对动子的平均驱动力(沿切线方向)为:
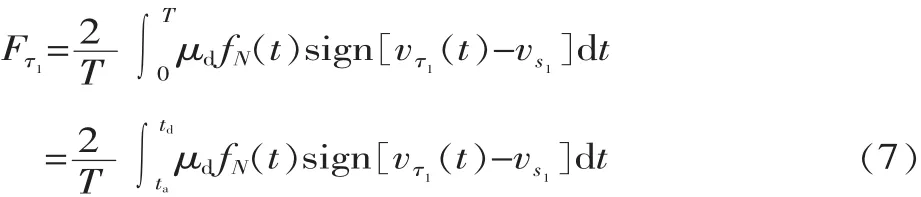
故十字形多自由度电机绕X轴旋转时输出力矩为:
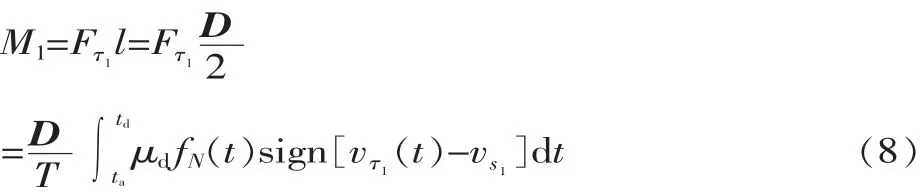
式中:l为驱动力的力臂;D为动子直径。
以上两式中的符号函数为:
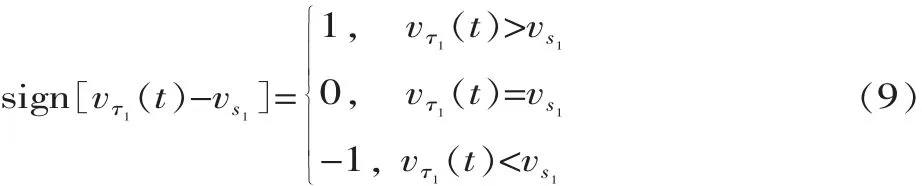
1.3 绕Z轴旋转时的定、动子接触模型
1.3.1 面外行波分析
十字形多自由度超声电机绕Z轴旋转时,将用正弦、余弦电信号同时激励出两个工作振动模态,此时定子驱动端产生行波来驱动动子,驱动足与动子间的接触比较连续平稳。根据赫兹接触理论,驱动足与动子间的接触力可分解为两个部分,即沿Z轴的接触力与沿径向的接触力。沿Z轴的接触力为:

式中:kZ为动子沿Z轴方向的等效弹簧刚度;δZ为动子沿Z轴方向的接触变形量,与定子振幅、动子接触刚度等相关。
根据库仑定律,驱动足与动子间的摩擦力为:

十字形多自由度超声电机绕Z轴旋转时,可将电机沿Z轴方向中心线展开,根据赫兹接触理论,此时定子与动子可等效于球体(定子)与面 (动子)接触的情况。故当仅考虑面外行波驱动时,驱动足与动子间的接触界面如图5所示。
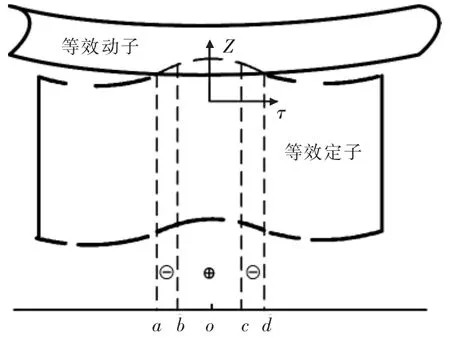
▲图5 驱动足与动子沿Z轴方向接触状况
在图5中,区间[a,d]为一个周期内接触区域,b、c点代表等速点,即定子振动速度与动子切向速度相同点。在[b,c]区域内,驱动足表面质点切向振动速度大于动子切向速度,这一区域内摩擦力做正功,定子对动子起驱动作用,该区域为驱动区间。在[a,b]及[c,d]区域内,驱动足表面质点切向振动速度小于动子切向速度,该区域内摩擦力做负功,定子对动子起阻碍作用,这些区域称为制动区间。
在分析定子、动子接触状况时,假设定子、动子材料具有弹性特性,根据赫兹理论,在沿Z轴方向预压力Fp作用下,接触区域的接触宽度为:
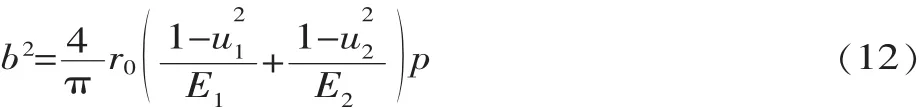
式中:r0为等效定子球体半径;E1为定子材料弹性模量;E2为动子材料弹性模量;u1为定子材料泊松比;u2为动子材料泊松比;p为单位长度上的载荷,且:
式中:L为定子与动子沿Z轴方向接触长度;Fp为动子对定子沿Z方向的作用力。
在接触区间[o,d]内,接触力沿切向τ(半径)方向的分布可表示为:

式中:q0为区间[o,d]上的最大应力,可表示为:

在接触区域内接触应力关于中点对称,因此区间[a,o]上的接触力也可用式(14)表示。驱动足与动子接触过程中,假定驱动质点切向运动速度与动子切向速度不同,则存在打滑,否则,两者相互黏结。结合库仑定律,定子对动子产生的驱动转矩为:
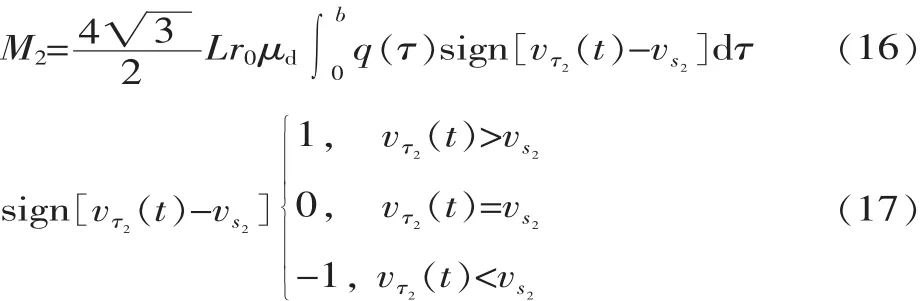
1.3.2 面内行波分析
当仅考虑定子产生的面内行波作用,其产生径向力可表示为:

式中:kr为动子沿径向的等效弹簧刚度;δr为动子沿径向接触变形量,与定子振幅、动子接触刚度等相关。
切向摩擦力可表示为:

此时,定、动子间的接触情况如图6所示,图中[a′,d′]为定、动子的接触区间,b′、c′为等速点,那么区间[b′,c′]为驱动区间,区间[a′,b′]及[c′,d′]为制动区间。
根据弹性接触理论[10-12],沿径向预压力作用下Fr的接触弧度α可表示为:


▲图6 驱动足与动子沿径向接触状况

式中:rs、r0为等效定子、等效动子的半径;Dα为Dund-urs参数。
最终,定、动子接触长度可表示为:

在接触区间[o,d′]内,接触 力沿切向分布力为:

由于接触区域内的接触力关于原点对称,故区间[a′,o]内的接触力亦可用式(23)表示。面内行波产生的转矩为:
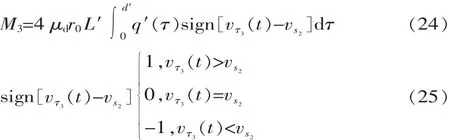
式中:L′为定子与动子沿Z轴方向接触长度;vτ3(t)为驱动足表面质点切向速度。
综上所述,绕Z轴旋转时输出力矩为:

2 机械特性仿真及分析
根据所建立的十字形多自由度超声电机接触模型,利用MATLAB进行仿真计算,分析电机各参数对电机输出性能的影响,有助于了解十字形多自由度超声电机在不同条件下的工作状态及输出性能,为电机设计提供参考。
2.1 仿真参数
表1为进行仿真计算时所采用多自由度电机的相关参数的基值。研究其中某参数对电机输出性能的影响时,取表中基值附近范围内的值进行仿真分析。

表1 电机的仿真相关参数
2.2 电机参数对其性能的影响
2.2.1 定子振幅对电机输出特性的影响
定子振幅与定子材料、结构、尺寸以及驱动电压的幅值等相关,其它参数确定的情况下,在一定范围内,定子振幅会随驱动电压幅值的增大而增大。图7所示为定子沿Z轴的振幅对电机输出力矩与输出速度关系特性曲线的影响。在保持其它参数不变的情况下,改变定子沿Z轴方向振幅时,电机的最大输出力矩及空载速度随着定子振幅增加而增加,且空载速度比最大输出力矩对振幅的改变更敏感。
2.2.2 摩擦因数对电机输出特性的影响
定子与动子间的接触摩擦因数是影响电机输出特性的最重要因素之一。因此,为了解动摩擦因数对动子输出特性的影响,对不同摩擦因数时的输出响应进行仿真分析。图8为只改变摩擦因数、其它参数不变的情况下输出力矩与输出速度的关系曲线,从图中可以看出,电机的最大输出力矩随着摩擦因数的增大而增大,而空载速度保持不变。
2.2.3 驱动频率对电机输出特性的影响
图9为驱动频率对电机输出特性影响的仿真曲线,从图中可以看出,随着驱动频率偏离共振频率越来越远,电机的输出特性越来越差,因为驱动频率偏离共振频率时,电机的振动幅值会随之显著减小。因而,选取合适的驱动频率可以显著提高电机工作时的输出性能,且可通过调节驱动频率来控制电机的输出特性。
3 样机试验
利用所研制的多自由度超声电机进行了样机输出特性试验。
3.1 驱动电压与转速关系
压电陶瓷片工作电压过高时容易被击碎,工作电压太低时运行效率低,为获得较为合理的工作电压,测量了超声电机驱动电压与转速的关系曲线。

▲图7 定子振幅WZ对电机输出特性的影响
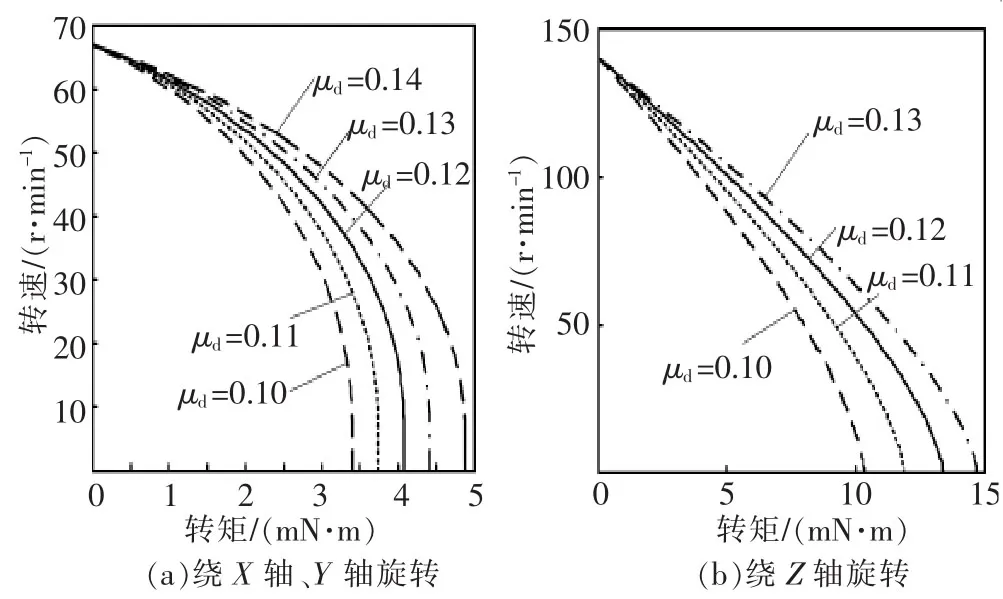
▲图8 摩擦因数对电机输出特性的影响

▲图9 驱动频率fw对电机输出特性的影响
利用信号发生器(Tektronix AFG3022)与功率放大器(HFPA-41)为电机供电。在动子上作标记,使用摄像机记录一段时间内动子的运动情况,再根据摄像计算平均转速。以26 kHz为激励频率,测试驱动电压峰峰值从100~250 V变化时的电机转速,如图10所示。电机绕X、Y、Z轴的转速随激励电压的增加而增加,可通过控制激励电压的大小来获得不同的电机转速。其实驱动电压减小时,电机的驱动振幅也减小,进而影响电机的转速。从图7仿真曲线可以看出,振幅减小时,计算出来的电机空载速度也在减小,其与图10测试的电机转速变化趋势基本一致。
3.2 驱动频率与转速关系的试验
实测样机在不同驱动频率下的转速,以获取驱动频率对电机转速的影响规律。当驱动电压峰峰值为250 V时,测得电机在25.2~26.8 kHz激励频率范围内绕X、Y、Z轴的转速。其中当驱动频率分别为25.6 kHz、26 kHz、26 kHz时,电机绕X、Y、Z轴旋转的最高转速分别为:55.4 r/min、55 r/min和125.5 r/min。根据该驱动频率与转速的关系曲线,可以通过改变驱动频率的方法来控制电机的转速。从图9驱动频率对电机输出特性的仿真曲线可看出,驱动频率偏离共振频率时,计算出的电机空载转速将变小。这与图11试验测试的电机转速变化趋势基本一致。
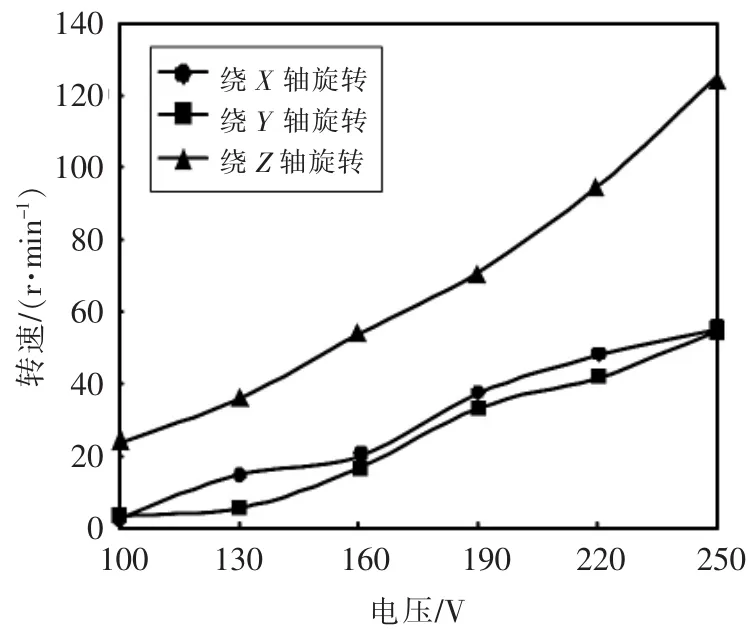
▲图10 驱动电压与转速的关系曲线

▲图11 驱动频率与转速的关系曲线
4 结论
建立十字形多自由度超声电机摩擦接触模型。由于该电机动子绕X、Y轴旋转与绕Z轴旋转的驱动机理不同,该模型利用弹性接触理论进行了分别考虑。
利用所建立的接触分析模型,对多自由度电机机械特性进行了估算,分析了定子振幅、摩擦因数、驱动频率对电机输出性能的影响规律。
对研制样机的机械特性进行了测试,测试结果与仿真计算结果的变化趋势基本一致,表明所建立模型对十字形超声电机的预估是有效的。本分析模型能有助于十字形多自由度电机的特性仿真分析和优化设计。
[1]赵淳生.超声电机技术与应用[M].北京:科学出版社,2007.
[2]李志荣,黄卫清,赵淳生.多自由度超声电机研究的一些新进展 [J].振动、测
试与诊断,2003,23(3):161-164.
[3]张健滔,金家楣,赵淳生.新型多自由度圆环型驻波超声电机[J].振动与冲击,2011,30(12):223-225.
[4]姚志远,吴 辛,赵淳生.行波超声电机定、转子接触状态试验分析[J].振动、测试与诊断,2009,29(4):388-391.
[5]周盛强,赵淳生.超声电机接触界面的两种简化有限元模型[J].振动、测试与诊断,2009,29(3):251-255.
[6]Takashi M,Takayuki T,Akiro M.Finite-element Analysis of the Rotor/Stator Contact in a Ring-type Ultrasonic Motor[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1992,39(6):668-674.
[7]Joachim P S,Peter H,Miao Bingqi.A Note on the Contact Problem in an Ultrasonic Travelling Wave Motor[J]. International Journal.Non-Linear Mechanics,1996,31(6):915-924.
[8]刘锦波,陈永校.超声波电机定转子接触的摩擦传动模型及其实验研究[J].中国电机工程学报,2000,20(4):59-63.
[9]曲建俊,孙凤艳,田秀.粘弹性接触层在定子表面的行波超声电动机接触模型[J].机械工程学报,2006,42(12):175-179.
[10]龚中良,黄平.基于非连续能量耗散的滑动摩擦系数计算模型[J].物理学报,2011,60(2):383-388.
[11]龚中良,黄平.基于热力耦合的滑动摩擦系数模型与计算分析[J].华南理工大学学报(自然科学版),2008,36(4): 10-13.
[12]Michele Ciavarella,Paolo Decuzzi.The State of Stress Induced by the Plane Frictionless Cylindrical Contact.Ⅱ. The Case of Elastic Similarity[J].International Journal of Solids and Structures,2001,38(26-27):4507-4523.
(编辑 丁 罡)
In cross-type multi-DOF Ultrasonic Motor,the drive mechanisms are different when the rotor rotates around X axis and Y axis or rotates around Z axis.So that they should be treated separately in accordance with the elastic contact theory and a model is established to analyze the frictional contact of the motor.The established model is used to estimate the mechanical properties of the cross-type multi-DOF ultrasonic motor and analyze the regular pattern involving the impact of the stator amplitude,the friction factor and driving frequency to the output performances of the motor.The test results of the mechanical properties of the prototype show that,The established model is valid for prediction of the characteristics of cross-type multi-DOF ultrasonic motor,it may provide guidance in design of the cross-type multi-DOF ultrasonic motor.
Multi-DOF Ultrasonic Motor Contact Model Simulation Analysis Mechanical Properties
TH122;TM356
A
1000-4998(2015)10-0006-06
*国家自然科学基金资助项目(编号:51305248)
上海市自然科学基金资助项目(编号:13ZR1416900)
上海大学创新基金资助项目(编号:SDCX 2012025)
2015年4月

