基因-疾病关联研究meta分析中存在合并基因型的贝叶斯分析策略*

第二军医大学卫生统计学教研室 (200433)　

宋嘉麒　金志超△　贺　佳△

基因-疾病关联研究常利用单核苷酸多态性(single nucleotide polymorphisms,SNPs)筛查与疾病相关的基因突变位点,然而由于样本量和统计效能的问题,常常导致假阴性,利用meta分析对原始研究进行定量合并,能够有效地提高统计效能。

在进行基因-疾病关联研究meta分析时,常常遇到遗传模型的假定问题。遗传模型的假定问题既存在于原始文献中,也存在于meta分析定量合并时。如果原始文献中研究者主观地进行了遗传模型的假定,如假定为显性或者隐形遗传模型,在其结果中有可能只给出特定遗传模型下的效应量(OR值),从而使meta分析作者无法同时获得三种基因型的频数,最终导致其在定量合并时也不得不采用原始文献中的遗传模型,或者将该研究剔除。Minelli,Salanti等人对遗传模型的假定问题进行了较为深入的研究[1-2]。Salanti等人的研究已经能够较好的处理上述两种遗传模型假定的情况[2],利用贝叶斯方法分析遗传模型假定而存在的基因型合并问题。但是在实际研究当中,由于Salanti等人提出的贝叶斯方法较为复杂,且对于常用的回顾性似然未提供代码(回顾性似然更适合采用病例对照研究的基因-疾病关联研究[3]),使得此方法在实际应用中使用的并不广泛。同时,Salanti等人在其研究中并未对遗传模型的选择提供结论。

本研究将在Minelli和Salanti等人研究的基础上,利用回顾性似然和贝叶斯方法处理基因-疾病关联研究meta分析中存在的原始文献基因型合并的问题,构建一个遗传模型选择指示概率,以数据驱动估计各种典型遗传模型存在的相应概率,最后提供相应的JAGS代码和R代码用以实现上述过程,为其他类似研究提供方法学支持。

方　　法

1.基本原理

常见的进行基因关联研究的原始文献会提供如表1所示的病例组和对照组的三种基因型的频率,假定三种基因型分别时AA、Aa和aa。

表1　常见基因关联研究的数据表现形式

表1中cni(n=1,2,3)表示纳入的某原始研究病例组三种基因型频率,病例组样本量为ci,tni(n=1,2,3)为对照组三种基因型频率,对照组样本量为ti。病例组和对照组基因型频率服从多项分布,可用(1)式和(2)式表示:

(1)

(2)

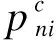
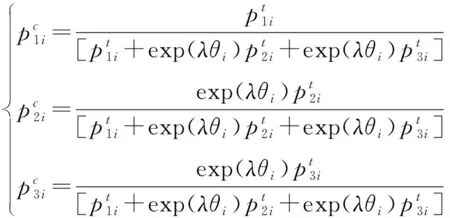
(3)

式中系数λ表示遗传模型,λ=0表示隐性遗传模型,λ=0.5表示共显性遗传模型,λ=1表示显性遗传模型。式(3)是在病例组和对照组所有基因型都可以从纳入文献中获取的情况下使用,但在纳入的原始文献中,作者在分析时有可能对遗传模型进行假定,得到的是一个对基因型频数进行合并了的四格表,如表2所示。

表2　假定遗传模型下合并基因型的基因关联研究数据表现形式

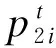
(4)

在估计φi时,假设感兴趣的等位基因A的频率为κi,根据哈代-温伯格平衡(Hardy-Weinberg equilibrium),φi=2(1-κi)/(2-κi)。相比利用极大似然估计等方法,贝叶斯方法在估计合并效应量θ时更方便,能够方便地借助外部信息,如哈代-温伯格平衡。

2.实例

实例数据来自Huang等发表的关于ACE I/D基因多态性与肾移植预后关系的系统综述[4],本实例选取了肾移植所致的急慢性排斥反应,共纳入11项研究,其中9项提供了完全的基因型频数,2个研究存在合并的基因型频数(II和ID基因型存在合并)[5-6],其基本信息如表3所示。

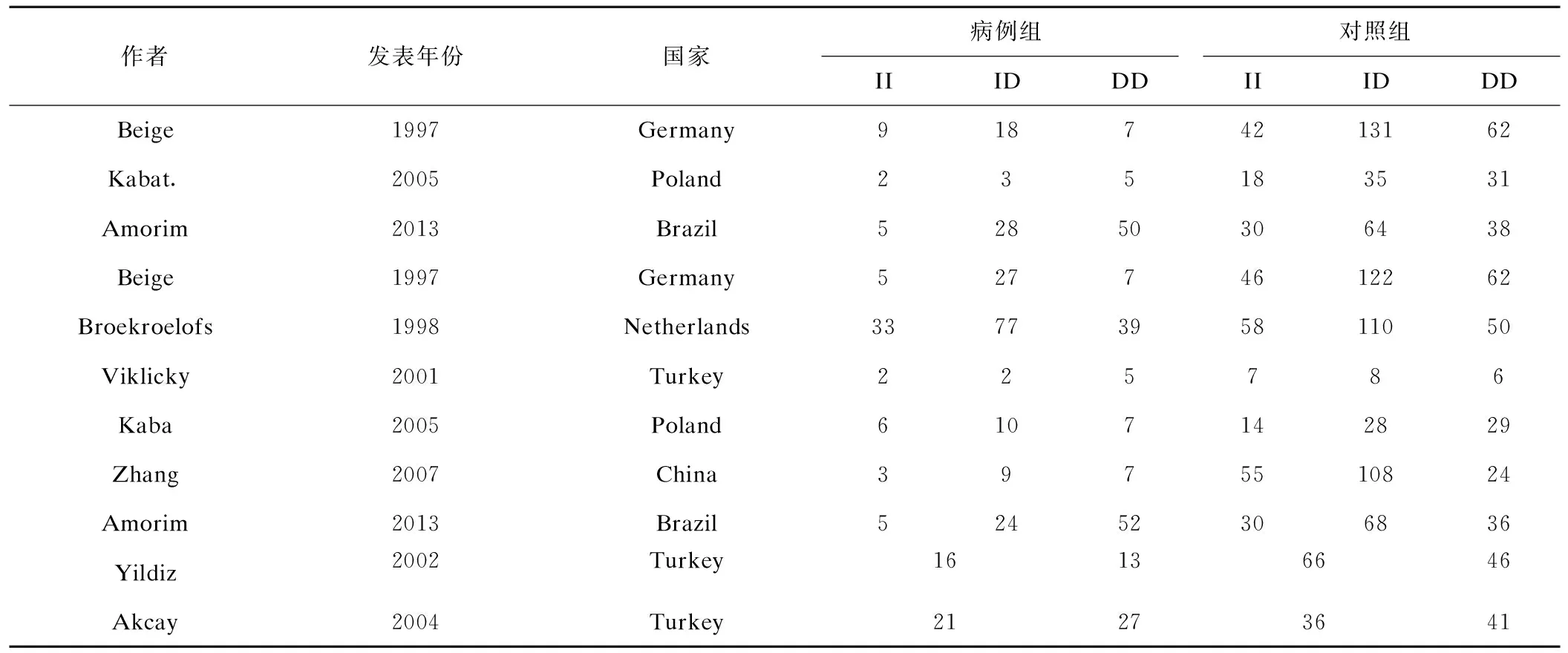
表3　 ACE I/D基因多态性对肾移植所致的急慢性排斥反应纳入文献基本信息

3.软件实现

本研究采用贝叶斯常用软件JAGS,并利用R软件中的R2jags包调用执行。由于文章篇幅所限,本例中只提供关键的JAGS代码,R代码可通过邮件向通讯作者索取。JAGS完整代码如下:

model{

#Complete studies

for(i in 1:9){

#Multinomial Likelihoods.matrix ′ca′ and ′co′ is 9*3

ca[i,1:3]～dmulti(p.case[i,1:3],tcase[i])

co[i,1:3]～dmulti(p.cont[i,1:3],tcont[i])

# 公式(3)

sum1[i]<-p.cont[i,1]+exp(lambda*theta[i])*p.cont[i,2]+exp(theta[i])*p.cont[i,3]

p.case[i,1]<-p.cont[i,1]/sum1[i]

p.case[i,2]<-exp(lambda*theta[i])*p.cont[i,2]/sum1[i]

p.case[i,3]<-exp(theta[i])*p.cont[i,3]/sum1[i]

for(k in 1:3){

p.cont[i,k]～dunif(0,1)

}

}

#Merged studies

for (i in 1:2){

#Multinomial Likelihoods.matrix ′ca.merg′ and ′co.merg′ is 9*2

ca.merg[i,1:2]～dmulti(p.casemerg[i,1:2],ca.n.merge[i])

co.merg[i,1:2]～dmulti(p.contmerg[i,1:2],co.n.merge[i])

#公式(4)

p.contr[i,1]<-p.contmerg[i,1]

p.contr[i,2]<-p.contmerg[i,2]*f[i]

p.contr[i,3]<-p.contmerg[i,2]*(1-f[i])

sum2[i]<-p.contmerg[i,1]+exp(lambda*theta[i+9])*f[i]*p.contmerg[i,2]+exp(theta[i+9])*(1-f[i])*p.contmerg[i,2]

p.case1[i,1]<-p.contr[i,1]/sum2[i]

p.case1[i,2]<-exp(lambda*theta[i+9])*p.contr[i,2]/sum2[i]

p.case1[i,3]<-exp(theta[i+9])*p.contr[i,3]/sum2[i]

for(k in 1:2){

p.contmerg[i,k]～dunif(0,1)

p.casemerg[i,k]～dunif(0,1)

}

#H-W平衡

f[i]<-2*(1-pa[i])/(2-pa[i])

pAA[i]<-(1-pa[i])*(1-pa[i])

n1[i]～dbin(pAA[i],co.n.merge[i])

pa[i]～dbeta(1,1)

}

for(i in 1:11){

theta[i]～dnorm(mean,prec)

}

# Priors information for effects and heterogeneity

mean～dnorm(0,0.0001)

tau ～ dnorm(0,1)I(0,) #半正态分布

prec=1/(tau*tau)

#Probability of genetic model,0:recessive model,0.5 co-dominant,1:dominant

d<-c(0,0.5,1)

p<-c(1/3,1/3,1/3)

K～dcat(p[])

lambda<-d[K]

#Results of interest

OR2<-exp(mean*lambda)

OR3<-exp(mean)

#probmodel[1]:recessive,probmodel[2]:co-dominant,probmodel[3]:dominant

for(g in 1:3){

probmodel[g]<-equals(K,g)

}

}

上述代码的关键部分为涉及合并基因型的回顾性似然构建和编码,对于τ还可以有其先验分布,如dgamma(0.001,0.001)和dunif(0,10)等。

结　　果

上述实例中,相对于基因型ACE D/D,携带有基因型I/I和基因型I/D的肾移植患者发生排斥反应风险无统计学意义,其OR值和95%置信区间分别为0.68 (0.41,1.02)和0.50(0.19,1.04),用以表示遗传模型的系数λ及其95%置信区间为0.53 (0.50,1.00),其后验概率密度分布如图1所示。三种遗传模型的概率分别为隐性遗传模型为0%,显性遗传模型6.2%,共显性遗传模型为93.8%。研究间变异τ2=0.98。

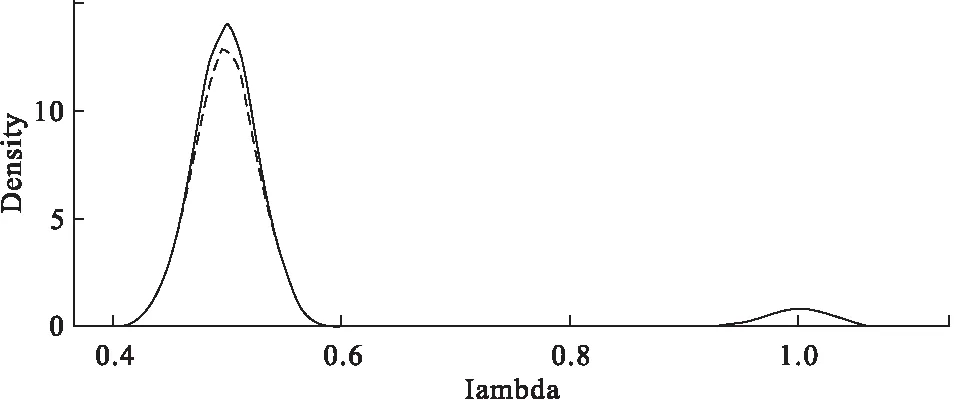
图1　表示遗传模型的系数λ的后验概率密度

另外,我们又选取了Ragland等发表的关于UCHL1 S/Y基因多态性与帕金森氏病发病风险关系的系统综述[7],共纳入18项研究,全部提供了完全的基因型频数。首先用无遗传模型约束的贝叶斯Meta分析方法[8-9]估计OR值,然后无放回地随机抽取2个研究,合并S/Y和Y/Y基因型频数,并用本研究方法估计OR值,并重复9次。结果如表4所示,相对于基因型S/S,基因型Y/Y的OR值为0.876～0.912,均值为0.895,与纳入全部研究的估计结果0.894相近,基因型S/Y的OR值为0.649～0.734,均值为0.704,与纳入全部研究的估计结果0.704相近。

表4　随机合并S/Y和Y/Y基因频数及全部研究OR值估计结果

讨　　论

本研究采用了贝叶斯方法处理了基因-疾病关联研究meta分析中原始文献中存在遗传模型假定而带来基因型合并问题。在meta分析过程中不假定基因

型,利用完整的研究和哈代-温伯格平衡估计合并基因型中每个基因型的频率,由于纳入了所有原始文献,未剔除存在合并基因型的研究,能够提高统计检验效能。利用Ragland等人实例提供的完全数据表明本文方法估计OR值的稳定性、准确性以及精确性均较高。

同时,利用本研究的方法,在无充分生物学机制的基础上,能够利用数据驱动估计几种经典遗传模型的概率。利用meta分析的方法估计遗传模型对于构建慢性传染性疾病的发病或预后模型具有重要意义[2]。在宏观环境危险因素的基础上,利用合理的遗传模型加入基因层面的影响因素,能够使预测模型更为精确,能够促进精准医学的开展。

本研究存在的主要缺陷是哈代-温伯格平衡在少量的研究中并不一定成立,因此需要考虑在哈代-温伯格平衡不成立条件下的似然函数形式[10]。另外,本研究未对影响合并结果的其他因素如种族、检测方法、性别等考虑在内,可以进一步考虑在贝叶斯框架下使用meta回归,使得结果更为合理。