自适应修正电子时间引信的空炸与弹道炸判定问题研究
杨宇鑫,李豪杰,原红伟,于 航
(南京理工大学 智能弹药技术国防重点学科实验室,江苏 南京 210094)
电子时间引信、计转数定距引信等空炸引信,都是在弹道上某点给出发火信号而作用[1-2]。文献[3]在智能空炸引信的引爆概率方面进行了研究,主要对近炸引信的炸高概率进行分析,而对空炸引信没有进行分析。文献[4]提出了基于四台光电探测靶与一个高分辨率面阵CCD相机相结合的近炸引信空中炸点的三维坐标测试方法。文献[5]利用短时傅立叶变换对弹道弹丸旋转信号进行视频分析,分解出不同的误差因素类型,提出了三类误差修正的策略。文献[6]以自测速修正电子时间引信为例,在弹丸飞出炮口后效期后,测量弹丸的实际炮口速度,并计算初速改变量,通过存储于引信内的时间模型对装定的引信作用时间进行修正,而由于引信炸点随机散布的影响,造成引信空炸实际炸点与预定炸点有些许偏差。引信的弹道炸是由于解除保险后引信发火系统在弹道上受到干扰而提前意外发火[7-9]。
上述文献分别对引信空炸与弹道炸的概率问题以及影响因素进行了研究,但对于两者的区分问题,并没有做深入的探索。本文从自适应修正电子时间引信的角度,分析2种发火模式的机理,并结合累积分布函数,提出一种判定引信空炸与弹道炸的方法。
1 空炸作用概率的求解
1.1 2种发火机理的分析
引信弹道炸即是,在引信解除保险之后,在预定作用点之前,由于受到意外干扰,包括信息型干扰和能量型干扰,引信发火控制系统意外产生发火输出信号,从而激发已经处于待发状态的引信。引信弹道炸的概率一般规定小于千分之一,在外弹道上解除保险点之后,可以认为是平均分布。
引信空炸即是,在引信解除保险后,在预定作用点附近,根据预先的指令信息或者非接触探测到的目标信息,引信发火控制系统正常产生发火输出信号,从而激发已经处于待发状态的引信。引信正常作用的概率,根据产品特性,一般规定在一定的置信度下,发火作用可靠度不小于某值(例如陆军某引信,置信度0.9,作用可靠度不小于0.92)。引信正常作用时,作用点的散布一般服从正态分布。
1.2 引信的定位模式分析
根据一般分析准则,对于某件事情的定位,主要看引起该事件的各种因素的概率,可将现象出现的原因归结于概率大的因素。
例如在弹道上某点作用,原因A引起的概率为PA,原因B引起的概率为PB,则根据定位原则,定位为原因A的条件为PA>PB,定位为原因B的条件为PA 对单个引信而言,通常有4种状态。第1种是正常工作状态,即正常空炸状态,其概率分布用F1(x)表示;第2种是完全失效状态,如瞎火,它的概率分布是F2(x);第3种是早动状态,即引信弹道炸,其概率分布为F3(x);第4种是迟动状态,它的概率分布为F4(x)。除完全失效状态F2(x)外,其他3种状态如图1所示[3]。图中,纵坐标f(x)为引信炸点概率密度函数,横坐标x为炸点距离,l为标定位置,l±Δl为引信空炸正常工作区间。 3种状态的概率分布函数为 (1) (2) (3) (4) 通常单个引信的作用距离按正态规律分布在其标定值l上下,其概率密度函数为 (5) 式中:f(x)为引信炸点概率密度函数,Pa为引信的动作可靠度。 由式(3)并根据上节所提到的引信的定位模式可知,当PA=PB时,为引信弹道炸与空炸的临界过渡点,所以当F3(x)=F1(x)时,则l-Δl即为引信空炸与弹道炸的分界点。将式(5)代入式(3),得: (6) 因此,求出参数σ,并最后解出l-Δl的值是本文的关键。本文尝试用累积分布函数的方法,令: F2(x)=F3(x) F1(x)=F(x) 即将引信在l-Δl处弹道炸概率与该处的正常空炸概率进行对比。 累积分布函数表示随机变量小于或等于某个数值的概率P(X≤x),正态分布的累积分布函数不是显式的初等函数,其值可以通过函数逼近等方法近似得到[10]。在本文中,可以用累积分布函数Fp(x)表示引信在早动状态下发火的概率,以x表示正常发火时的概率,然后利用函数逼近的方法,使引信弹道炸引起的概率与引信空炸引起的概率相等后,求出边界值。即有: (7) 正态分布的累积分布函数能够由误差函数的特殊函数表示: (8) 式中:μ为引信理想炸点位置,Gauss的误差函数为 (9) 实数erf(x)∈[-1,+1]。 标准正态分布的累积分布函数由误差函数的特殊函数表示为 (10) 简化可得: (11) 令引信弹道炸的概率为PB,控制空炸区间为Pa-PB的上下区间,即可得到分界点。根据此分界点判断引信是空炸还是弹道炸。已知空炸炸点散布服从正态分布。在对引信空炸概率散布模型的分析时,可以采用式(7)~式(10)进行分析计算。在有效区域内,空炸的作用率Pz、空炸精度可由指标中给出。 因此,确定空炸与弹道炸边界的关键在于,找出空炸炸点散布正态分布函数中占比为Pa-PB的分界点,即是空炸与弹道炸的边界。在结合空炸作用率的同时,求解出正态分布函数中参数σ的值,以及Pa-PB处分界点与目标炸点的距离。为了求解简便,以空炸精度和空炸作用率为切入点,求出参数σ的值,最后反求出Pa-PB处的边界值l。 令空炸精度为T,建立标准正态分布累积分布函数,且空炸的作用率约为Pz,根据式(11),则有: (12) 求出x的值。 由于空炸精度为T,则可以根据空炸精度与x的关系求出参数σ的值: (13) 上式完成了标准正态分布向正态分布的转化,以此可求出Pa-PB附近满足空炸精度条件下的分界点l值,得: (14) 得x1的值,则Δl=x1σ。 通过上述计算可以发现,引信完成空炸的作用区间在预定炸点的μ-x1σ处,可以认为,预定炸点的μ-x1σ所在的点即是空炸与弹道炸的边界点。 结合考核指标,自适应修正电子时间引信弹道炸的概率小于千分之一,令完全失效状态的概率为0,控制空炸区间为99.9%的上下区间,即可得到分界点,其空炸误差为±8 m,空炸作用率为80%,预定炸点为距发射距离400 m处,代入式(13)~式(15)进行计算,得Δl=29.374 5 m,由于所求值为弹道炸与空炸边界,即据发射距离370.625 5 m处(约为371 m)所在的点是空炸与弹道炸的分界点。 本文提出了以累积分布函数求解引信空炸与弹道炸边界的方法,由以上分析和计算可知,以自适应修正电子时间引信为例,在预定炸点为400 m,求得引信空炸与弹道炸分界点为371 m处。在试验中,可以根据该算法,对试验引信进行正确的评估。试验表明,当检测出引信的发火位置在理想发火位置附近时,可以依照边界点来判断是空炸作用还是由于提前解保而出现的弹道炸。这种算法可帮助军方与制造方更好地检验引信的性能。 [1] 丁立波,张合,马少杰. 计转数空炸引信自适应炸点控制技术[J]. 南京理工大学学报,2011,35(5):600-603. DING Libo,ZHANG He,MA Shaojie. Adaptive burst point control technique for turns count air burst fuze[J]. Journal of Nanjing University of Science and Technology,2011,25(5):600-603.(in Chinese) [2] 李豪杰,云赛英,李长生,等. 高原环境下电子时间引信炸点控制修正方法[J]. 弹道学报,2016,28(3):48-52. LI Haojie,YUN Saiying,LI Changsheng,et al. Correction method of burst control of electronic time fuze in plateau environment[J]. Journal of Ballistics,2016,28(3):48-52.(in Chinese) [3] 彭兴平,马宝华,熊永虎. 智能空炸引信系统的引爆概率研究[J]. 探测与控制学报,1999,21(3):7-9. PENG Xingping,MA Baohua,XIONG Yonghu. The study on the initiation probability of an intelligent air burst fuze system[J]. Journal of Detection & Control,1999,21(3):7-9.(in Chinese) [4] 李静,雷志勇,王泽民,等. 近炸引信对空炸点位置测试方法研究[J]. 计算机测量与控制,2011,19(7):1 602-1 604. LI Jing,LEI Zhiyong,WANG Zemin. Research on test method of anti-air proximity fuze burst location[J]. Computer Measurement & Control,2011,19(7):1602-1604.(in Chinese) [5] 马少杰,张合. 空炸引信定距误差分类及修正策略[J]. 弹道学报,2008,20(3):75-78. MA Shaojie,ZHANG He. Classification and modification for ranging error of air bursting range fuze[J]. Journal of Ballistics,2008,20(3):75-78.(in Chinese) [6] 云赛英. 自测速修正电子时间引信精度控制技术研究[D]. 南京:南京理工大学,2015. YUN Saiying. Research on precision control technology on self-measuring velocity and correcting electronic time fuze[D]. Nanjing:Nanjing University of Science and Technology,2015.(in Chinese) [7] 张武凤,王雨时,张宏,等. 惯性触发开关动态特性与引信弹道炸分析[J]. 探测与控制学报,2016,38(3):35-40. ZHANG Wufeng,WANG Yushi,ZHANG Hong. Analysis of inertial impact switch dynamic characteristics and fuze ballistic explosion[J]. Journal of Detection & Control,2016,38(3):35-40.(in Chinese) [8] 何小健,王劲,程剑,等. 碰击开关锡晶须与引信弹道炸[J]. 探测与控制学报,2011,33(2):1-4. HE Xiaojian,WANG Jin,CHEN Jian,et al. Tin whisker on impact switch and fuze ballistic explosion[J]. Journal of Detection & Control,2011,33(2):1-4.(in Chinese) [9] 刘猛,曲凡军,倪庆杰,等. 某底排弹引信弹道早炸原因分析[J]. 弹箭与制导学报,2015,35(2):69-72. LIU Meng,QU Fanjun,NI Qingjie,et al. Reason analysis on early explosion of fuze trajectory of certain BB projectile[J]. Journal of Projectile,Rockets,Missiles and Guidance,2015,35(2):69-72.(in Chinese) [10] 王晶晶,杨正瓴. 累积正态分布函数的逼近函数综述[J]. 计算机应用,2014(S2):83-84. WANG Jingjing,YANG Zhengling. Review of approximating functions to cumulative normal distribution function[J]. Journal of Computer Applications,2014(S2):83-84.(in Chinese)2 用累积分布函数求解引信空炸与弹道炸边界
2.1 单个引信的工作状态
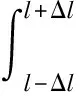



2.2 累积分布函数
3 算例
4 结束语

