面向心电信号的低功耗压缩感知电路设计*

黄 翔， 潘天文， 魏朋博， 孙益洲， 虞致国， 顾晓峰

0 引 言

受电池寿命的影响，心脏状态的长时间监测往往受到设备功耗的限制。因此，降低系统功耗成为面向心电(electrocardiogram,ECG)信号的植入式医疗设备迫切需要解决的一个问题[1～3]。

将压缩感知(compressed sensing，CS)理论应用于无线心电传输来降低系统功耗成为了近年来的研究热点。理论优势在于对原始稀疏信号的重构只需要很少的数据量，且其数据采集端的压缩过程相对简单，可以满足低功耗的要求[4,5]，而相对复杂的重构过程可在手机或其他终端实现[6]。Mamaghanian H等人利用扩展频谱随机调制预积分器，实现了一种CS模拟信息转换硬件电路，但其信号压缩是在模拟端实现的，易受噪声干扰[7]。Dixon A M等人研究了针对心电和肌电传感器的系统，采用阈值法和小窗滑动改善心电信号的时域稀疏度，可达到16倍的压缩因子(compression factor，CF)，但阈值法的引入破环了原始信号，导致恢复精度不够理想[8]。Chen F等人提出了一种比较通用的CS系统架构[3]，具有结构简单、功耗低且恢复精度较高的特点，但并未针对心电信号进行功耗优化。

本文在Chen F等人提出的结构基础上[3]，针对ECG信号的周期性进行低功耗优化。计算数据压缩过程中运算产生的最大数据，确定电路中累加器的位数即压缩数据的位数，避免使用冗余寄存器，以减少电路功耗、提高数据的CF，降低了发射模块的功耗。采用贝叶斯学习算法[9]对压缩数据进行重构以验证所设计电路的功能。

1 基于CS系统框架

在CS理论中[10]，用一个M×N维观测矩阵Φ将待压缩的N维心电信号f投影到一个低维的测量空间上，得到压缩后的M维压缩信号y(M≪N)

y=Φf=ΦΨx=ACSx

(1)

式中Ψ为稀疏基；x为f在稀疏基下的稀疏表示，ACS=ΦΨ称为CS矩阵。由于M≪N，式(1)为一个欠定方程，解不具有唯一性。考虑到x是f的稀疏表示，可以通过求解凸优化问题算出式(1)的最优解x*，再利用f*=Ψx*重构出原始的心电信号。

根据CS理论，一种基于CS的心电信号采集系统被广泛采用，其系统框图如图1所示。

图1 CS系统框架

该系统的前端主要有模/数转换器(ADC)和CS模块。ADC将模拟心电信号转化为数字信号f，CS模块用观测矩阵Φ与f相乘得到包含原始信号信息的M维压缩信号y，再将y经过并串转换由发射模块发射到终端，在终端利用y重构出心电信号。

2 CS电路及功耗优化

2.1 CS电路

CS模块主要由CS采样和并/串转换2个子模块组成，CS采样模块通过矩阵生成模块和累加器完成矩阵乘法运算，以实现心电信号的压缩功能，即

(2)

CS模块的电路实现如图2所示。其中，Φ1[n],Φ2[n],…,ΦM[n]分别为观测矩阵Φ中第M行对应的行向量，例如，Φ1[n]=[Φ11,Φ12,…,Φ1N]。

图2 CS模块电路结构示意

在硬件实现中，本文选择随机伯努利矩阵作为观测矩阵Φ。在进行矩阵乘法运算时只需做加减运算，不用做复杂的乘法运算，降低了硬件的复杂性。M的大小需要预先设定，若M过大，占用过多的面积;过小，导致压缩的数据所包含的信息量不足以准确重构原始数据。N为一组待压缩信号的个数，可配置，通过改变N值改变压缩比CF=(N×Bf)/(M×By)，其中Bf和By分别为输入的心电信号的位数和累加器的位数。Bf由ADC的位数确定，当ADC的位数大于8时其分辨率的提高并不会显著影响信号的重构质量[11]，考虑到低功耗的要求，Bf暂定为8。此外，采样频率的选择也会影响电路性能。若频率过大，对于一个周期的心电信号，采样过多的数据，造成功耗浪费；若采样频率;过小，则采样数据过少，导致包含的信息量无法在压缩之后重构出原始信号。文献[12]的实验结果表明在20 kHz的采样频率下，当M=50，N=1 024时可以使传输的数据量和重构的效果达到平衡。

根据M，N的值，确定矩阵生成模块的设计，电路结构如图3所示，矩阵生成模块由2组线性反馈移位寄存器组成，在每个时钟周期并行产生50个伪随机的0或1的数据，且每1 024个时钟循环一次。

图3 矩阵生成模块

2.2 电路功耗分析

上述电路结构中需要50个累加器，累加器功耗占了CS采样模块总功耗的较大部分，因此主要对累加器的功耗进行分析。本文参考逻辑功效 (logical effort，LE)模型分析累加器模块的功耗[13]。对该模型进行适当的简化，发现电路的动态功耗Pdyn可由每个节点的寄生电容值和开关频率决定[11]

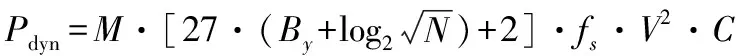
(3)

式中C为反相器参考电容值；fs为累加器输入数据的频率及开关频率。LE模型并不能计算出电路的亚阈值电流，为了计算漏电功耗，引入电源电压V下的反相器参考漏电流Ileak[11]，则漏电功耗Pleak可表示为

(4)

由式(3)、式(4)可知，在M，N，V一定的情况下，要想减小系统的功耗应尽量使By即累加器的位数最小。但对于不同的信号源，By不确定。为了防止累加结果溢出，通常将By设置得足够大(ADC输出位数的2倍)[3]。然而，心电信号具有一定的周期性和峰值，因此，在有限的累加过程中(N次累加)可以确定压缩过程中产生的最大数据，从而确定By，避免不必要的功耗和资源浪费。

2.3 电路功耗优化

为确定CS采样模块所需要的最小累加器位数，本文采用MIT-BIT心率不齐数据库[14]中的心电数据，计算压缩过程中累加过程所产生的最大数据。

以第一组1 024个心电信号的压缩过程为例说明，根据式(2):1)计算第1行累加过程中的最大值，即Φ11f1,Φ11f1+Φ12f2,Φ11f1+…+Φ1NfN这1 024个数的绝对值的最大值，用max_row表示；2)依次计算得到第2行到第50行的max_row；3)比较这50个max_row的值，得出第一组数组压缩过程中产生的最大数据max。依次类推，计算第2，3，…，N组数据压缩过程产生的最大值，最终比较得出整个心电信号压缩过程产生的最大数据，根据该数据确定累加器的位数。

由于数据库中的采样频率为360 Hz，而电路设计的采样频率是20 kHz，因此，需要预先对心电数据进行插值处理，并转换为8位二进制ADC数据，以模拟20 kHz采样的心电数据。取第一组1 024个心电数据，计算矩阵乘法，并求出观测矩阵每一行压缩过程中产生的最大值max_row，该过程计算结果如图4所示，横轴表示观测矩阵Φ的某一行，纵轴表示对应第x行累加过程中的最大值。

图4 第一组心电信号压缩产生的最大值

由图4可知，50个max_row中最大的为2 524，因此，max=2 524，重复上述过程，取100组信号，求出每一组计算过程中的最大值max。该过程计算结果如图5所示，横轴表示所取组的序号，纵轴表示对应第x组数据压缩过程产生的最大值max。

图5 各组心电信号压缩产生的最大数据

由图5可知，这100组数据中的最大值为3 725，且图中各组心电信号的max具有一定的周期性。虽然该最大值由限组数据统计得到，但由于心电信号的周期性，13位有符号二进制数最大可表示4 095可以满足计算要求，且对心电信号的准确重构亦验证了这一结论。若不进行这一步优化，对于8位心电数据，为避免结果溢出会选用16位的累加器[3]。采用13位累加器代替16位累加器，减少了电路中的冗余设计，可降低电路的静态和动态功耗。

2.4 电路功耗分析

采用SMIC的65 nm工艺库，利用Synopsys的工具对设计进行综合及功耗计算，为较准确评估功耗优化效果，对电路加入I/O PAD单元。在时钟频率为20 kHz下优化前后压缩感知电路功耗对比如表1所示。

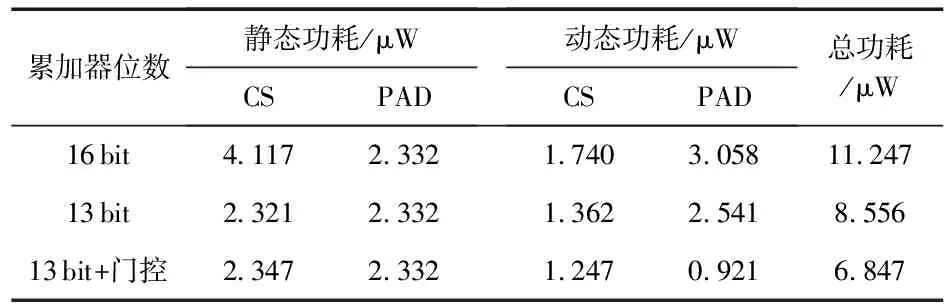
表1 电路优化前后功耗对比

其中13 bit+门控表示插入门控时钟的13位累加器构成的CS电路，CS表示由CS采样与并串转换模块组成的CS模块,PAD表示电路的I/O PAD。用13位累加器代替16位累加器，电路的总功耗降低了23.93 %(由11.247 μW减少到8.556 μW)，其中CS模块的静态功耗显著减少了43.62 %。CS模块的门数由原来的42 071减小到25 029，减小了40.51 %，这是功耗降低的主要原因。另外由于累加器位数的减小使得每个压缩数据y的位数减小，降低了PAD的翻转频率，从而降低了PAD的动态功耗。为进一步使得电路功耗降低，在综合时采用门控时钟技术，当部分单元进入空闲状态时关断相应的时钟树分支，既可以关闭相应单元，还可以消除时钟网络上冗余的电平翻转。门控时钟的加入使得电路功耗降低到了6.847 μW，较不加入门控时钟功耗降低了19.97 %。2种优化方法使得电路功耗降低了39.12 %。结果表明本文的优化方法可以明显降低系统的功耗，更好地适应了植入式设备的要求。

另外，随着累加器位数的减小，最终数据的压缩比由原来的10((1 024×8)/(50×16))提高到了12((1 024×8)/(50×13))，另一方面输出数据位数的降低也使得无线发射模块的功耗降低。

3 仿真与验证

3.1 电路仿真

根据上述设计与优化方法完成寄存器转换级(register transfer level,RTL)设计，仿真波形如图6所示。以图2中计算y1为例说明(y1,y2,…,y50是并行产生的)，xin为输入的8位心电信号(时钟上升沿采样)，q表示矩阵生成模块产生的观测矩阵Φ中的第一行对应的行向量Φ1[n](1执行加法，0执行减法)，acc_out为每个时钟上升沿根据xin和q,计算出的累加结果，当一组心电信号压缩结束后，产生复位信号acc_rst(高有效)，累加结果即y1由yout寄存输出，同时acc_out重新对下一组心电信号进行累加计算。

图6 压缩感知电路仿真波形

3.2 重构验证

为评估重构信号的质量，将压缩信号通过贝叶斯学习算法进行重构[9]，原始信号与重构信号如图7所示。该算法与传统的重构算法相比更适用于高数据压缩比和噪声变化的心电信号。

图7 原始信号与重构信号

为具体评估所重构的信号质量，本文采用均方根百分比(percentage root-mean-squared difference,PRD)指标来量化生物信号的信息丢失[12]

(5)

式中x(n)为原始信号；x(n)为重构信号。计算得出贝叶斯学习算法重构信号的PRD=1.14 %,可以满足临床应用的要求[10]。

4 结 论

对一种心电信号CS电路进行了低功耗优化设计。针对心电信号的周期性，通过减少电路模块中的冗余寄存器数目降低功耗，并采用门控时钟技术，发现2种方法使电路的功耗降低了39.12 %。另外，由于减少了传输数据的位数，一方面提高了信号的CF，另一方面发射模块的功耗亦得到了显著降低。利用贝叶斯学习算重构信号的PRD=1.14 %，符合临床应用对ECG信号的要求。

参考文献:

[1] 陈伟伟,高润霖,刘力生,等.《中国心血管病报告2015》摘要[J].中国循环杂志,2016,31(6):624-632.

[2] 江培海,黄启俊,常 胜,等.基于SoC FPGA的心电信号检测系统设计[J].传感器与微系统,2016,35(2):74-77.

[3] Chen F,Chandrakasan A P,Stojanovic′ V.A signal-agnostic compressed sensing acquisition system for wireless and implantable sensors[C]∥Custom Integrated Circuits Conference,San Jose,2010:1-4.

[4] 韩思辉.基于FFS的压缩感知算法研究[J].自动化技术与应用，2016,35(4):30-35.

[5] 赵 磊,俞阿龙,徐冬平,等.压缩感知在传感器节点信息采集中的应用[J].传感器与微系统,2016,35(8):141-143.

[6] 屈信超,张 跃.基于压缩感知的实时心电信号压缩算法[J].计算机工程与设计,2014,35(10):3450-3454.

[7] Mamaghanian H,Khaled N,Atienza D,et al.Design and exploration of low-power analog to information conversion based on compressed sensing[J].IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2012,2(3):493-501.

[8] Dixon A M,Allstot E G,Gangopadhyay D,et al.Compressed sensing system considerations for ECG and EMG wireless biosensors[J].IEEE Transactions on Biomedical Circuits and Systems,2012,6(2):156-166．

[9] Zhang Z,Jung T,Makeig S,et al.Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse Bayesian learning[J].IEEE Transactions on Biomedical Engineering,2014,60(2):300-309.

[10] 熊 炜，芦 荻，刁文静，等.基于压缩感知的宽带跳频信号采集[J].无线电工程，2015,45(3)：34-36.

[11] Chen F,Chandrakasan A P,Stojanovic V,et al.Design and analysis of a hardware-efficient compressed sensing architecture for data compression in wireless sensors[J].IEEE Journal of Solid-State Circuits,2012,47(3):744-756.

[10] Chen F,Lim F,Abari O,et al.Energy-aware design of compressed sensing systems for wireless sensors under performance and reliability constraints[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2013,60(3):650-661.

[11] Sutherland I,Sproull B,Harris D.Logical effort:Designing fast CMOS circuits[M].San Mateo,CA:Morgan Kaufmann Publishers Inc.1999.

[12] Parkale Y V,Nalbalwar S L.Application of compressed sensing(CS)for ECG signal compression:A review[C]∥Proceedings of the International Conference on Data Engineering and Communication Technology,Singapore,2017:53-65.