基于霍夫变换的工位点识别算法设计与实现

仲崇权　赵亮

摘 要：针对插件机器人的视觉定位系统，提出了一种基于图像金字塔的霍夫变换算法，目标在于准确识别工位点坐标。改进的霍夫变换算法与传统的霍夫变换算法相比减少了非零像素点的计算，并且通过限定霍夫变换算法所使用的参数，减少了内存的使用以及计算量；沿着边缘点的梯度方向进行像素点的累加，通过先确定圆心再确定圆心所对应的半径的方法，用二维累加器替代复杂的三维累加器，从而降低了时间复杂度和空间复杂度，提高了算法的效率。实验结果表明，本算法能够准确的定位PCB板的工位点，可以较好的运用在插件机器人的插件过程中。

关键词：视觉定位；累加器；霍夫变换；图像金字塔

中图分类号：TP391.41 文献标识码：A 文章编号：2095-1302（2016）08-00-04

0 引 言

插件机利用机器视觉技术将一些有规则的电子元器件自动标准地插装在印制电路板导电通孔内的机械设备中[1]。工位点识别算法对工位点的获取起着至关重要的作用，直接影响到插件的准确度及效率。传统的霍夫变换方法是一种穷尽式搜索，其时间复杂度和空间复杂度都比较高。为了克服传统霍夫变换的缺陷，文献[2]提出了一种广义霍夫变换方法，理论上可以检测到任意指定曲线，但在实际应用中，当需要检测的目标物体发生旋转或者缩放时，广义霍夫变换的时间复杂度和空间复杂度的增长都很快；文献[3]提出的改进后的霍夫变换算法同时利用边缘像素的梯度和曲率来加速目标的检测，该改进算法能够成功的用二维累加器替代三维累加器，有效降低时间复杂度和空间复杂度，但由于直线的曲率是无穷大，当图像中存在由许多直线组成的物体时效果很不理想；文献[4]利用一对边缘点来建立查找表，这种改进方法也能够利用二维累加器代替三维累加器，但对于有部分目标物体被遮挡的图像，检测结果可能不太理想。

本文提出了一种基于霍夫变换的改进方法，该方法在不影响目标检测准确度的情况下，利用图像金字塔在低分辨率的图像上进行目标检测，减少了非零像素点，同时利用像素梯度以及对圆的半径加以限定的方法，先获取圆心再确定半径，用二维累加器替代复杂的三维累加器，降低了霍夫变换算法的复杂度，提高了该算法的效率，保证了工位点识别算法的准确性。

1 霍夫变换与图像金字塔

1.1 霍夫变换

霍夫圆变换是通过三维累加器获取圆心以及半径的一种方法[5]，具体如图1所示，图像上的点映射为一个三维空间中的圆锥面：（a-x0）2+（b-y0）2=r2，在xy平面，若三个点在同一个圆上，则它们对应的空间曲面相交于一点，这些点构成的边界接近一个圆形。假设一幅大小为M×N （其中M>N）的图像，其中非零像素点个数为Z，图像上的每一个非零像素点所对应的圆锥面可表示为三维累加矩阵G=[ga，b，r]M×N×N/2，将Z个矩阵进行累加则得到三维累加器，0≤j≤Z-1。此累加器空间的最大值对应原始图像的圆的参数ac，bc，rc：

1.2 图像金字塔

图像金字塔是一系列以金字塔形状排列的分辨率逐渐降低的图像集合，如图2所示。最初用于机器视觉和图像压缩。金字塔最底部是待处理的原始图像（高分辨率），顶部则是该原始图像的低分辨率近似。当金字塔向上移动时，尺寸和分辨率降低。

图3显示了一个构建两个密切联系的图像金字塔的简单系统，第j-1级近似输出提供建立一个近似值金字塔所需的图像，第j级预测残差输出用于构建一个补充的预测残差金字塔。在图3中，近似和预测残差金字塔都以一种迭代方式进行计算。在第一次迭代前，以金字塔形式描绘的图像放在这个近似金字塔的第j级中。

（3）将输入的第j级图像与（2）得到的预测图像做差，得到的结果即为第j级预测残差。由于插件机视觉处理部分的主要目标是获取mark点及工位点的坐标和半径，因此在霍夫圆变换算法中，获取圆的中心及半径即可，之后通过高层图像计算原始图像中的圆心坐标以及半径值。所以本文提出的霍夫圆获取方法不需要预测第j级残差，只需要第j-1级近似。

为了确定在实现过程中所用到的图像金字塔的层数，获取原始图像的第二层以及第三层金字塔的图像。通过图4的比较可以看出第三层金字塔图像的工位点细节丢失较严重，且由于分辨率较低，通过该图像所确定的工位点坐标会对误差较为敏感，导致工位点坐标误差较大，插件失败。因此选择原始图像的第二层金字塔图像。假设原始图像中非零像素点的个数为M，则二层金字塔图像中的非零像素点的个数为M/4。图4所示是该图像的金字塔结果。

2 基于图像金字塔的改进霍夫变换

霍夫变换算法是在金字塔高层的低分辨率图像上完成的，通过确定梯度方向沿着梯度方向对累加器进行累加，提高了获取霍夫圆的效率[7，8]；环境允许的范围内限制半径参数可以减少内存的使用及计算量，提高算法的运行效率。然而由于三维累加平面复杂度较高，本文提出的霍夫变换方法通过先确定圆心再确定半径的方法，将三维累加平面变为二维累加平面，降低了复杂度。

首先利用图像金字塔算法得到边缘二值图像的二层金字塔图像，假设图像大小为M×N（非零像素点个数为Z），此时图像分辨率降低，边缘点减少。对边缘图像f（x，y）中的非零像素点计算其局部梯度；根据已经限定的圆的半径范围，将半径在限定范围内的像素点在二维累加器A中进行累加，此累加器用来求圆心。累加的具体方法为：对于图像的一个非零像素点（a，b），利用Sobel算子，通过掩模来近似一阶导数ga和gb，具体如图5所示。

2.1 获取圆心

遍历获得的A二维累加器对于欲获取的圆心有三个限定条件：

（1）圆心不能处于图像的边缘；

（2）圆心在A二维累加器中的累加值必须大于设定的阈值param；

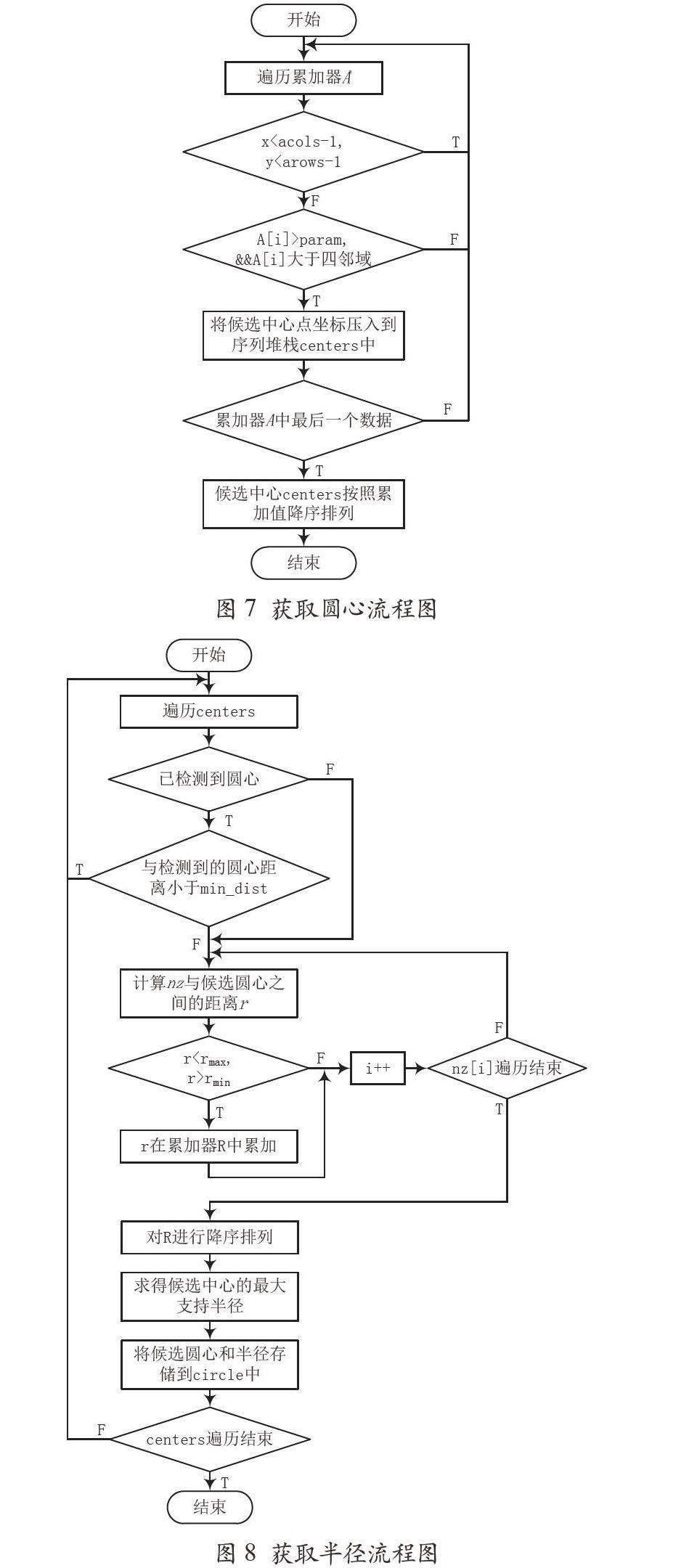
（3）圆心在A二维累加器中的累加值必须大于其四邻域的累加值。然后将其按照累加值进行降序排列，则累加值较高的点即为欲获取的圆心。获取圆心的流程图如图7所示。

2.2 获取对应圆心的半径

获取圆心对应半径的流程图如图8所示，若在获取候选圆心的过程中，centers中的候选圆心的个数是D，则对于每一个候选圆心（x0，y0），0≤o≤D-1。首先遍历存储圆参数的堆栈circle是否有已经确定了的圆的参数，若此时已经有检测到的圆的参数，则必须当其与已检测到的圆心点之间的距离大于设定的阈值min_dist（此阈值为欲获取的两个圆心之间的最小距离）时方可将该点视为欲获取圆心，同时遍历centers中的下一点；对R中的数据进行降序排列，即可得到该候选中心的最大支持半径。当遍历了centers中的每一个候选圆心点之后，circle中的值即为原始图像中通过本论文的改进的霍夫圆获取方法所得到的所有圆。

3 实验结果与分析

为了检验插件机器人工位点识别算法的准确性，对一个需要插入六个端子的PCB板进行插件测试，本实验通过Visual C++编程实现了基于霍夫变换的工位点识别软件。在实际的图像处理过程中，获取图像的视野大小可以设定为40 mm×30 mm，工位点的识别精度为0.01 mm，相机分辨率为40/0.01=4 000 pixcel（像素），另一方向是30/0.01=3 000 pixcel，即相机的分辨率至少需要4 000×3 000 pixcel，通过调研选择了一款有效像素为4 384×3 288的相机。

图9所示为实际插件过程中对工位点识别过程的截图，在实际测试过程中，该算法能够对工位点进行准确快速的定位，以完成插件功能，且实时性较好，插件的效率较高。

分析实验结果可知本算法在图像处理过程中对非零像素点的计算减少，降低了时间复杂度，提高了该算法的效率；同时利用二维累加器替代复杂的三维累加器，减少了处理内存空间的使用、降低了算法的计算量。因此本论文提出的基于霍夫变换的工位点识别算法准确度高，鲁棒性好，可以较好地用于插件机器人的插件过程中。

4 结 语

本文提出的基于霍夫变换的工位点识别算法能够准确高效的识别工位点，确定工位点的坐标。提出的基于图像金字塔的霍夫变换算法检测圆，在处理过程中减少了非零像素点的计算，提高了该算法的效率，保证了插件的实时性，避免了复杂的三维累加器的使用，利用二维累加器降低了时间复杂度和空间复杂度。实验结果表明，本算法能够准确识别PCB板的工位点，实现插件机器人的插件功能。研究成果已应用于某公司的插件机器人设备，满足了实际对PCB板进行插件的需求。本文提出的基于霍夫变换的工位点识别算法使得插件机器人的插件过程变得更加准确、稳定、高效。

参考文献

[1]黄震，顾启民.高精度机器视觉插件系统的研究与应用[J].组合机床与自动化加工技术， 2014（10）：105-108.

[2]张小军， 胡福乔.基于广义霍夫变换的芯片检测[J].计算机工程， 2009，35（23）：252-254.

[3] Yin Yaping， Wang Yanlin， Liu Guili， et al. The Detection of Quartz that Based on the Improved Hough Transform[J].Information Technology Journal， 2012，11（4）：560-562.

[4] Chen A J， Dong G H. Efficient Method for Rapidly Detecting Circles Based on Edge-Tracking[C]. Second International Symposium on Computational Intelligence and Design. Changsha， China. 2009：402-405.

[5]秦开怀， 王海颍， 郑辑涛.一种基于霍夫变换的圆和矩形的快速检测方法[J].中国图像图形学报， 2010，15（1）：109-115.

[6]许景波， 袁怡宝.圆度测量中的高斯滤波快速算法[J].南京理工大学学报， 2007，31（3）：342-345.

[7]魏锋， 王小林， 娄元静.基于图像处理技术的印刷电路板圆孔检测方法[J].河南理工大学学报（自然科学版），2013，32（1）：69-72.

[8]肖敏.基于机器视觉的晶圆定位系统研究[D].上海：上海交通大学，2013.