基于格的高效通用累加器与被累加值的零知识证明
谭子欣,邓 燚 ,马 丽
1中国科学院信息工程研究所 信息安全国家重点实验室 北京 中国 100093
2密码科学技术国家重点实验室 北京 中国 100878
3中国科学院大学 网络空间安全学院 北京 中国101408
1 引言
在过去,当用户需要访问数据,通常需要向数据管理者发送访问请求,然后管理者通过查表检查该用户是否具有访问权限。在这样的权限管理过程中,查表操作带来的开销往往会随着列表的大小呈线性增长,这样低效的管理方法显然将无法适应未来高速的大数据时代,为了解决这样的问题,1994年Benaloh和de Mare[1]提出了累加器的概念。累加器是指将某个集合中的所有元素压缩成一个较短输出,并能够为所有被累加值生成其对应的成员关系证据,通过成员关系证据可以向他人证明被累加值的成员身份,故而用户可直接将其身份和成员关系证据发送给数据管理者,数据管理者再通过一个确定的检验算法来判定该用户的合法性,这样的过程大大缩减了权限管理中的验证时间。除此之外,累加器在数字签名、匿名凭证、范围证明、集合成员关系证明等领域也有相当多的应用场景。
近二十年来,累加器的发展日新月异,功能性及安全性也在不断的更新和完善。1997年Barić和Pfitzmann[2]提出了无碰撞累加器的概念,并且首次给出了累加器的安全性定义。2002年Camenisch和 Lysyanskaya[3]提出了动态累加器的概念,即累加器增删元素的更新操作的时间复杂度独立于集合大小。2005年 Nguyen[4]提出了基于强Diffie-Hellman假设的动态累加器,2008年Damgård[5]和Triandopoulos又在此基础上设计出了能够支持非成员关系证明的双线性映射累加器。2007年 Jiangtao Li等人[6]提出了通用累加器的概念,同时基于强RSA假设实现了动态通用累加器。通用累加器既能为被累加成员生成成员关系证据,又能为非被累加成员生成非成员关系证据,而动态通用累加器则在通用累加器的基础上增加了动态更新的功能。到了 2012年 Camacho等人[7]和Lipmaa[8]分别独立研究出了能够去除可信第三方前提假设限制的通用累加器,前者是基于哈希树结构的通用累加器,后者是建立在欧氏环上的通用累加器。
随着量子计算的发展,人们开始忧心以往那些安全性基于强 RSA假设,离散对数假设等数论假设的累加器方案,未来在超高速量子计算机面前将会不堪一击,因而开始向格领域探索。2016年Libert等人[9]在利用基于SIS问题困难性假设[10]的抗碰撞哈希函数,构造出了第一个抗量子攻击的 SIS累加器,随后 Ling等人[11]在此基础上又提出了抗量子攻击的动态SIS累加器。2018年Libert等人[12]又设计出了基于 SIS问题困难性假设的通用累加器,同年Zuoxia Yu等人[13]设计出了首个基于SIS问题困难性假设的非成员关系累加器。
基于格上困难性假设的零知识证明系统通常有基于 Stern-like框架[9,11-15]和基于 Schnorr-like框架[16-20]两种模式。基于Stern-like框架的协议结合统计隐藏,计算绑定的承诺方案可以实现具有完美完整性以及统计零知识性的零知识协议,但缺点在于其单轮协议执行具有2/3的合理性错误,为了降低合理性错误,需要多次执行协议,所以整体执行效率低,在效率上不适用于现实场景; 而基于 Schnorr-like协议框架相对前者执行效率较高,且合理性错误较低,甚至可以实现单轮次执行合理性错误可忽略的零知识协议[1819],但需要拒绝样保证协议零知识性,因此存在一定的协议终止概率,不过可以通过参数设置将该终止概率降至任意小,所以相对前者更具有现实应用价值。
被累加值的零知识证明是指证明者以零知识的方式向他人证明自己知道一个累加器中的被累加值,即其所知秘密满足通用累加器成员关系验证算法,属于累加器在零知识证明领域上的一种应用。在过去,基于格上困难性假设的被累加值的零知识证明[9]和非被累加值的零知识证明[16]都主要采用 Stern-like协议框架来实现,却无法基于Schnorr-like协议框架来实现,主要原因在于该框架存在着知识的提取性错误,即无法保证提取出的证据满足范数限制要求或范围限制要求。今年Bootle等人[19]解决了这一问题,并基于 Schnorr- like协议框架实现了短秘密满足=m odq 的零知识证明,同时其1/n的合理性错误远小于基于 Stern-like协议框架实现的版本。同年,Rupeng Yang等人[20]基于Schnorr-like的协议框架实现了合理性错误1/poly的通用零知识协议框架,并且针对SIS累加器[9],提出了相应的被累加值的零知识证明方案[20],合理性错误可降低至1/poly。
1.1 本文贡献
本文在 SIS通用累加器[14]的基础上通过替换底层假设以及改进通用累加器的存储结构等手段,设计并实现了第一个基于 Ring-SIS问题困难性假设的通用累加器,可为被累加成员生成较短成员关系证据,也可为非被累加成员生成较短非成员关系证据; 该通用累加器打破了原有格上通用累加器[14]和非成员关系累加器[15]只能全局更新的限制,可实现局部更新; 图1展示的是本文设计的Ring-SIS哈希函数同 SIS哈希函数[15]在计算效率上的比较,当安全参数N越大,Ring-SIS哈希函数的计算效率越高。图2选用参数a1=64,N=171,此时 Ring-SIS哈希函数在计算效率上会低于 SIS哈希函数,但随着集合大小M的增加,Ring-SIS通用累加器存储结构带来的效率优势也越发明显,所以综合图1和图2可以得出结论: 随着安全参数N的增大或者被累加集合大小M的增大,Ring-SIS通用累加器内部计算效率以及更新效率要远优于以往的 SIS通用累加器[15]。实验结果表明本文所设计的通用累加器将更加适用于更新操作频繁且数据量更大的应用场景。
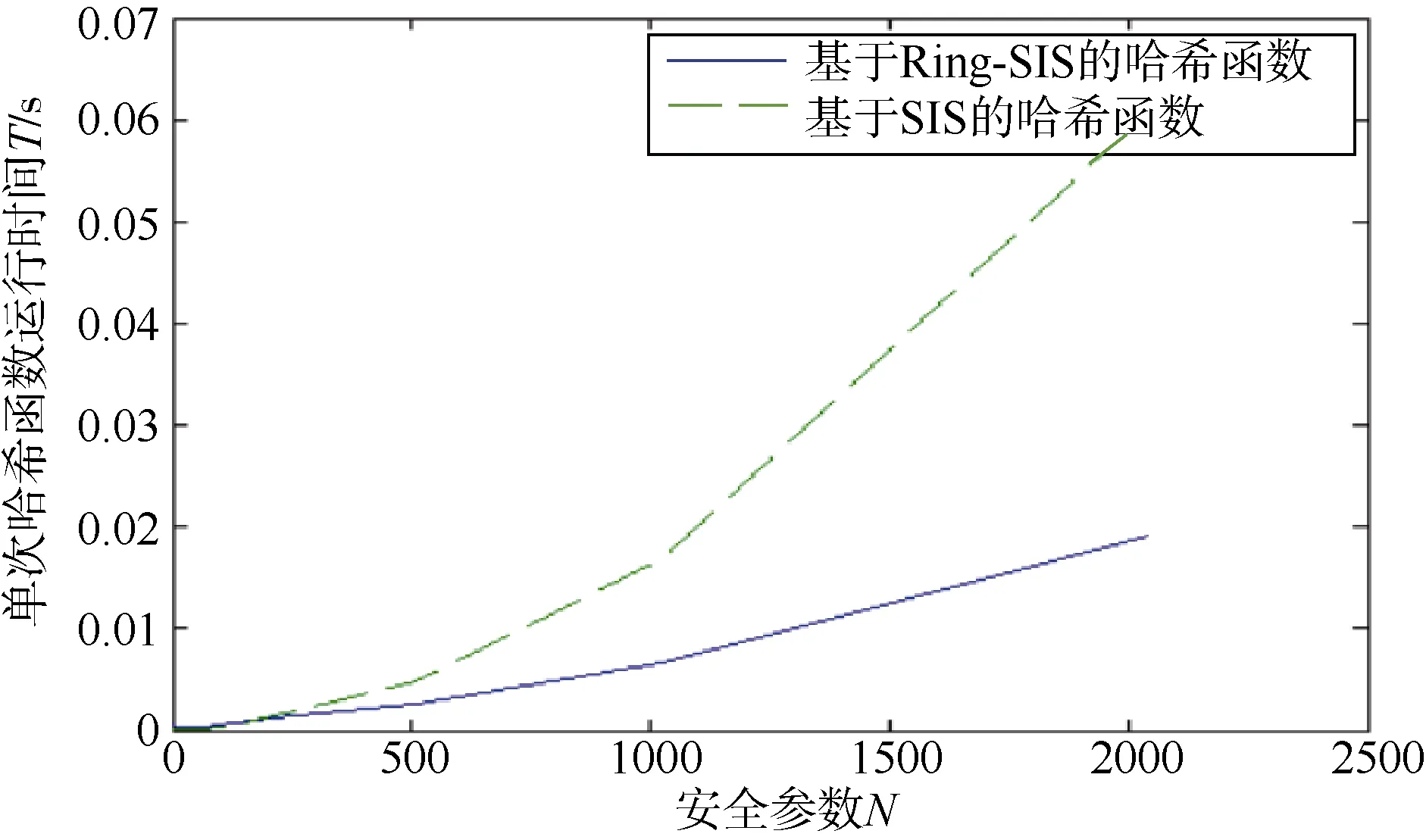
图1 当q=1024,Ring-SIS哈希函数与SIS的哈希函数运行时间对比图Figure 1 The comparison of execution time between the Ring-SIS hash function and the SIS hash function when q=1024

图2 当q=64,N=171,Ring-SIS通用累加器与SIS通用累加器单次更新运行时间对比图Figure 2 The comparison of single update time between the Ring-SIS accumulator and the SIS accumulator when q=64,N=171
另外针对本文所设计的 Ring-SIS通用累加器,本文基于 Schnorr-like协议框架,并选用尺寸大于2256的挑战值空间,设计出了第一个合理性错误可忽略的被累加值的零知识证明协议。表1所展示的是本文所设计零知识协议同以往协议[9,20]的工作比较。
1.2 本文结构
本文将在第 2章节给出全文所需要的准备工作,其中包括符号定义,密码学工具定义以及相关安全性定义; 第3章介绍了基于Ring-SIS问题困难性假设的通用累加器的具体设计以及通用累加器的安全性证明; 第4章详细介绍了Ring-SIS通用累加器所相应的被累加值的零知识证明协议,包括设计思路、具体构造以及协议的安全性证明; 第5章对本文工作进行了简要总结。
2 预备知识
2.1 符号定义
全文所需要用到的符号定义如表1所示。

表1 现有工作对比Table 1 The comparison of current schemes
2.2 工具介绍
2.2.1 格上问题与困难性假设
定义1(困难性假设)[21]已知环R,整数模数q≥2,整数l≥1,β﹥0和p≥1。给定多项式向量,对于任意概率多项式时间(PPT)算法求取一个非零短向量||e||p≤β是困难的。
定义2(问题)[18]已知环R,整数模数q≥ 2 ,整数k﹥n≥ 1,β﹥0和p≥1。给定一个随机矩阵,找到一个非零短向量y满足
根据[18]中的定义,如果存在算法A和函数ε,对无穷多个n,使得
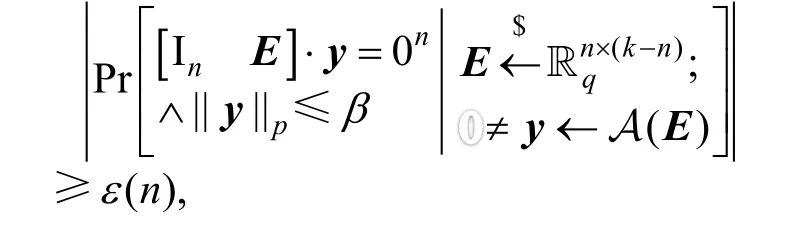
则称算法A能以优势ε(n)解决问题。
定义3(问题)[18]已知环R,整数模数q≥ 2 ,整数k﹥n≥ 1 ,β﹥0和p≥1。区分∙y的分布与上均匀随机分布,其中,且为非零短向量。且

表2 标记符注释列表Table 2 Tag comment list
根据文献[18]在定义,如果存在算法A和函数ε,对于无穷多个n,使得
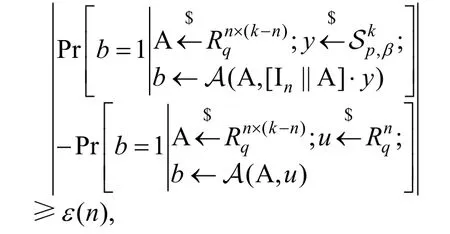
则称算法A能以优势1/poly(n)解决问题。
2.2.2 抗碰撞哈希函数
定义 4已知环R,整数模数q≥2,整数n,m≥ 0 。如果函数H:→满足下面三条性质:
易于计算: 对于任意x∊,H(x)能在多项式时间内计算完成;
压缩性:m﹤n;
抗碰撞性: 对于任意 PPT算法A,都存在一个可忽略函数ε,对所有安全参数n∊N,

则称函数H为抗碰撞哈希函数。
2.2.3 通用累加器
通用累加器主要由以下4个算法组成:
启动算法(Setup):输入安全参数N,输出一个公共参数pp;
累加器生成算法(Acc):输入公共参数pp和集合S,输出累加值u;
证据生成算法(Wit):输入公共参数pp、累加值u、元素δ以及类型type。当type=0,输出δ∊S的证据w,否则输出δ∉S的证据w;
验证算法(Ver):输入公共参数pp、累加值u、元素δ、证据w以及类型type。当type=0,验证w是否为δ∊S的证据,否则验证w是否为δ∉S的证据。
如果通用累加器对于所有的 PPT敌手A,都存在一个可忽略函数ε,满足:

则称该通用累加器是安全的。
2.2.4 知识的零知识证明
定义5(知识的零知识证明系统)对于NP关系P= { (x,w)} ∊ { 0,1}*× { 0,1}*,假设P为证明者,V为验证者,如果 P ( x,w) ,V ( x)是知识的零知识证明系统,则满足下面性质:
完整性:如果(x,w)∊P,则
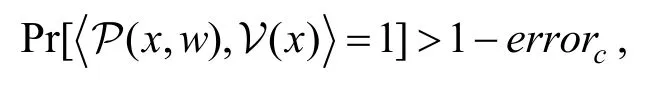
其中errorc为完整性错误。
m-特殊合理性:如果存在 PPT提取器,以P*,V ( x)产生的 m条合法副本 ( a,e1,z1),…,(a,em,zm)作为输入,可以输出证据w'满足(x,w ')∊P,其中对于任意 i,j ∊[m],ei≠ej。
诚实验证者零知识性:存在一个 PPT模拟器S,使得 S(x,r)输出副本 t r′ = ( a ′,e′ ,z′)的分布与验证者V诚实执行协议 P ( x,w) ,V ( x)所输出副本的分布是计算不可区分,其中r为诚实验证者使用的随机数。
2.2.5 正态分布与拒绝抽样
在域 RN上的,期望值为 v ∊RN同时标准差为σ﹥ 0 的正态分布,其概率密度函数通常被定义为

本文所使用的是在域 Rk上,期望值为 v ∊Rk,标准差为 σ ﹥ 0 的离散正态分布,其分布函数被定义为

下面是关于正态分布随机抽样的范数界限定理和拒绝抽样定理。
定理1[18,23]对于任意

当k∙N足够大时,该范数界限成立的概率接近于1。
定理 2[23]集合V为 Rm中所有||∙||2﹤T 的元素构成的子集,同 时h:V→R为一种概率分布。存在常数 M =O(1 ),使得算法A与算法F输出分布的统计距离将小于
算法A:
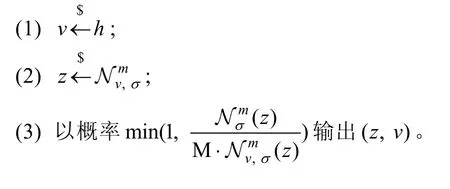
算法F:
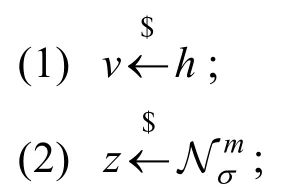
由文献[23]可知,如果对于任意正整数α,令σ=α ∙T ,则 M = e xp(12/α + 1 /(2α2))。算法A将会以至少的概率正常输出,且其输出分布与算法F输出分布之间的统计距离将小于
2.2.6 挑战值空间
挑战值空间是指验证者在收到来自证明者的第一轮消息后,选择挑战值的值域空间,通常挑战值空间的尺寸需要足够大,才能为了保证零知识证明协议较低的合理性错误,所以本文选择挑战集 合当N=512,其大小满足 | C |=﹥2256。
定理 3[18,24]当N,d为 2的幂次,且满足N≥d﹥ 1,模质数满足 q ≡ 2 d + 1 mod4d,则
(1) 多项式xN+1可以分解为d个不可约多项式:
(2) 对于所有 y ∊Rq{0}且满足或,在域Rq中可逆。
2.2.7 承诺方案
承诺方案由承诺阶段Com和打开阶段Open组成。在承诺阶段,承诺者S和接收者R需要先执行一个交互协议或者非交互协议,为一个具体的承诺方案生成所需参数,如消息x。然后S从自身的随机带中是随机挑选一个随机数r,计算承诺值c = C om(x;r),并将c发送给接收者; 在打开阶段,S将被承诺的消息x和随机数r发送给R,R随即通过验证 c = C om(x;r)来判断x,r是否为c的被承诺值。

另外,当算法 R*被限制为多项式时间算法,则上述承诺方案是计算隐藏的,当不限制算法 R*的计算能力,则称承诺方案是统计隐藏的。
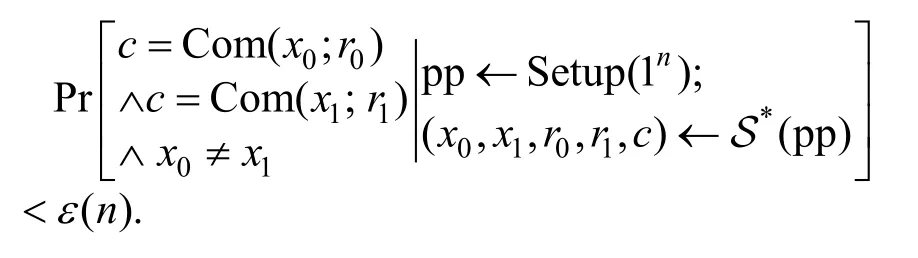
另外,当算法 S*被限制为多项式时间算法,则上述承诺方案是计算绑定的,当不限制算法 S*的计算能力,则称承诺方案是统计绑定的。
本文所构造的知识的零知识证明方案,需要使用具有加法同态性质的承诺方案,形如:

承诺方案主要用于保证协议的零知识性,故而选用文献[17]中的多项式向量承诺方案,具体算法如下所示:
密钥生成算法(CkeyGen):输入安全参数(1n,1k),输出公共参数,其中
承诺算法(Com):输入消息,选择随机数计算承诺值:
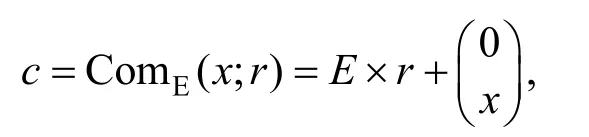
然后承诺者将c发送给接收者。
验证算法(Verify):承诺者向接收者发送接收者验证:
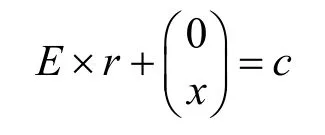
是否成立;
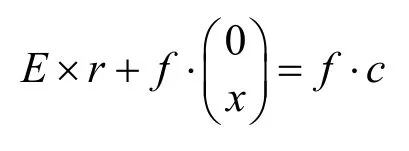
是否成立。
定理4[17]如果存在算法A能以优势ε打破承诺方案ComE的隐藏性,则存在算法 A ′在相同时间量级内以优势ε解决问题。
定理5[17]如果存在算法A能以概率ε打破承诺方案ComE的绑定性,则存在算法 A ′在相同时间量级内以优势ε解决问题。
3 通用累加器设计
目前已有的 SIS通用累加器[13,15,16],都是基于Merkle哈希树的结构实现的,而哈希函数作为哈希树的主要部件,决定着累加器的安全性和计算的整体效率。另外,对于以往SIS通用累加器,都要求叶子节点呈升序排列,故而每当有成员的加入或是撤销,都需要重新排序,再计算整棵Merkle哈希树。所以本文设计通用累加器的大致思想是通过替换哈希函数的底层假设,从根本上提升内部计算效率。同时,将单棵哈希树结构拆分成多棵子树结构,如图3所示,当通用累加器需要更新时,只需对被操作元素对应的子树进行重新计算,通过局部更新来实现通用累加器更新效率的大幅度提升。本节将主要介绍基于Ring-SIS的哈希函数以及基于Ring-SIS的通用累加器的具体构造。

图3 Ring-SIS通用累加器设计图Figure 3 The design of the Ring-SIS universal accumulator
3.1 抗碰撞哈希函数
在给出高效通用累加器算法之前,本节首先将介绍保证高效通用累加器安全性的基础部件:基于Ring-SIS问题困难性假设的抗碰撞哈希函数。本文所使用的哈希函数为了能与树型累加器所需要的数据形式相结合,在一般背包函数形式的哈希函数[25-26]的基础上稍作修改,具体构造如下所定义:
定义 6(哈希函数)给定模数q,整数,向 量 a =(a1,… ,以多项式环向量作为输入,哈希函数Ha定义为
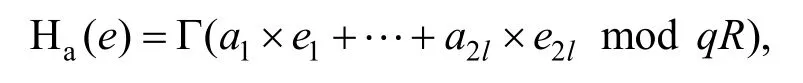
操作 Г : = Rq→被定义为 Г (t) = ( cl,… ,c1),其中另外对于所有i∊[N]与
由上面哈希函数的结构可以推出:
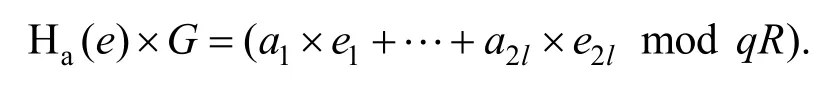
定理6如果问题对于所有PPT算法是困难的,则上述给出的哈希函数Ha是抗碰撞哈希函数。证明.假设函数Ha不是抗碰撞的,则存在PPT算法A和一个多项式poly(∙),对于无穷多个n,
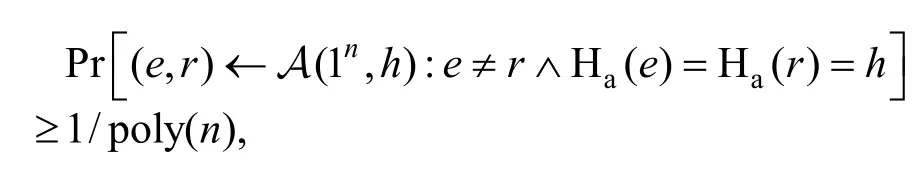
即至少能以1/poly(n)的概率找到一对碰撞(e,h0)和(r,h1)满足下面关系:
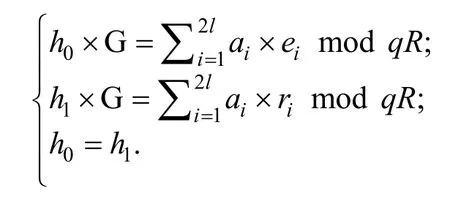
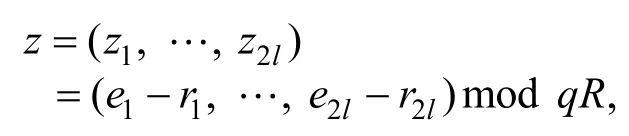
3.2 通用累加器
本文设计的高效通用累加器是以3.1小节中基于Ring-SIS问题困难性假设的哈希函数Ha为基础部件,一共涉及四个基础算法以及一个通用累加器更新算法。
令p=l∙N- 2 ,另外要求安全参数N使得p满足 p = 2g0,其中g0为正整数。这里定义被累加值的选择空间为:

其中
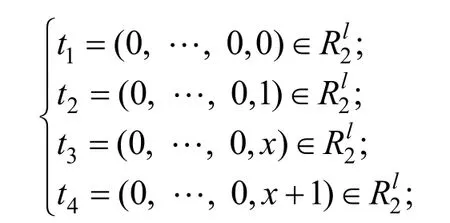
另外,对于 F irstj与Lastj的定义将在随后的启动算法中给出。
启动算法(Setup):
(1) 输入安全参数N。
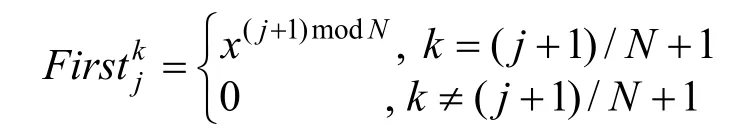
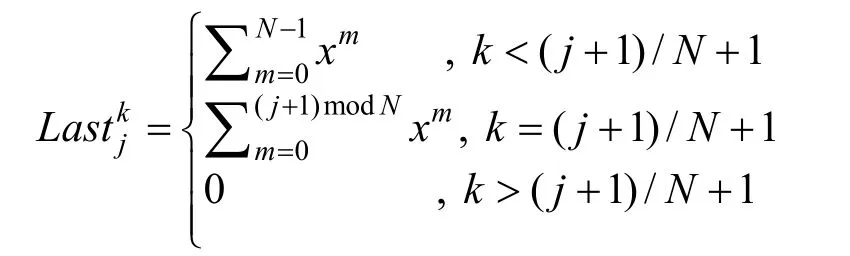
(3) 输出公共参数为 p p = {a,{F irstj,L astj}j∊[p]}。
累加器生成算法(Acc):
1) 输入公共参数pp以及升序集合S⊆K。
2) 将集合S按照如下方法划分为p个互不相交的升序子集,即 S = { Si}i∊[p]。对于任意s=(sl,… ,s1)∊Si,要 求deep(ptbl(s) ) - 2 =i,其 中deep(ptbl(s) ) ∊[l ∙N ]表示比特串ptbl(s) ∊ { 0,1}l∙N中的从右至左的非零最高位。
3) 对于所有子集Si,∀i∊[p],加入辅助元素,各自计算新的子集通过算法对新子集计算子树 Ti,并返回 Ti的根rooti。

证据生成算法(Wit):
2) 当type=0且δ∊S,输出关于δ∊S的证据w:
(1) 令 nd= d eep(δ),i =nd- 2 ,故 δ ∊ Si⊆ S 。
(2) 在子树 Ti中找到元素δ对应的叶子节点,则关于δ∊S的证据可以表示成如下形式:

其中

(3) 输出证据w。
3) 当type=1且δ∉S,输出关于δ∉S的证据w:
(1) 令 nd= d eep(δ),i =nd- 2 ,故 d ∉Si。
(3) 在子树 Ti中找到 δ0,δ1对应的叶子节点,即元素δ∉S的证据可以表示成如下形式:
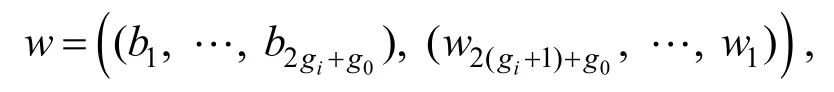
其中
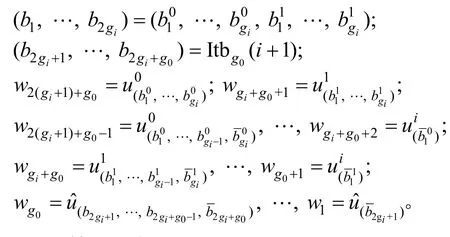
(4) 输出证据w。
验证算法(Ver):
1) 输入公共参数pp,元素δ∊K,证据w,累加值ˆu以及类型标识type。
2) 当type=0,检查是否δ∊S:

若
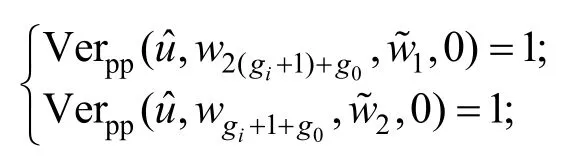
同时满足,则输出1。
累加器更新算法(AccUpdate):
1) 输入公共参数pp,被操作元素δ∊K以及操作标识opt。
2) 当opt = 0 ⋀ δ ∉ S ,表示向通用累加器中添加新元素δ:

3) 当opt= 1 ⋀ δ ∊ S ,表示从通用累加器中删除元素δ:
(1) 令 i = d eep(δ) - 2 ,将δ从升序子集Si⊆S中删除,得到新的升序集 Si=Si/δ,此时 ki=|Si|。
(2) 随后按照步骤2中的(2)至(4)执行,最终输出最终树T更新后的根节点Root。
3.3 安全性分析
定理 7如果问题对于所有 PPT算法是困难的,根据 2.2.3小节中通用累加器的安全性定义可知,3.2小节给出通用累加器ACC是安全的。
证明.假设ACC不是安全的,则存在一个PPT敌手算法B以及一个多项式poly(∙),对于无穷多个N,使得

然后可以利用敌手算法B构造出另一个 PPT敌手算法A来打破哈希函数Ha的抗碰撞性,进而打破格上问题的困难性假设,以此证明假设的矛盾性 。
令事件A为δ∊S,同时PPT算法B能伪造δ∉ S 的有效非成员关系证据; 令事件B为δ∉S,同时PPT算法B能伪造δ∊S的有效成员关系证据,根据假设可以得出:

令事件C为存在一个PPT算法找到哈希函数Ha的一对碰撞,那么事件C发生的概率
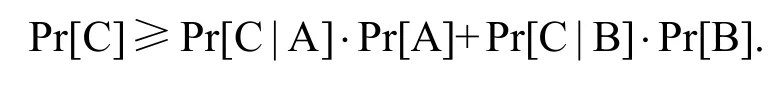
下面将讨论: 在事件A发生的前提下,事件C发生的概率。
若δ∊ S ⋀ t ype= 1 ,令 i = d eep(δ) - 2 ,则算法B伪造的证据为
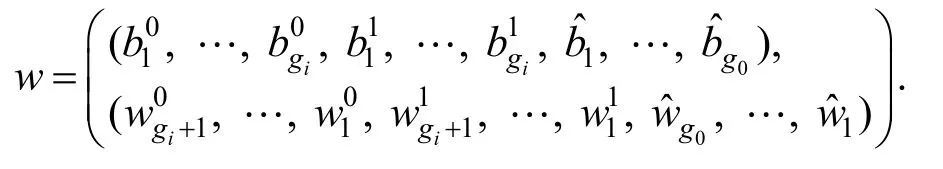
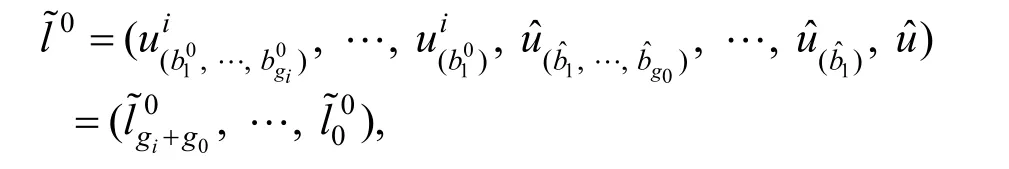
子树 Ti中叶子节点至最终树T中根节点Root的路径:
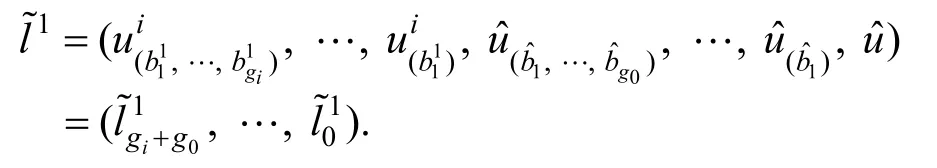
另外通过验证算法 V erpp(,δ,w,1 )可以计算出路径:
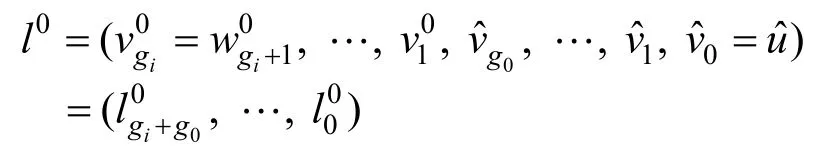
和路径:
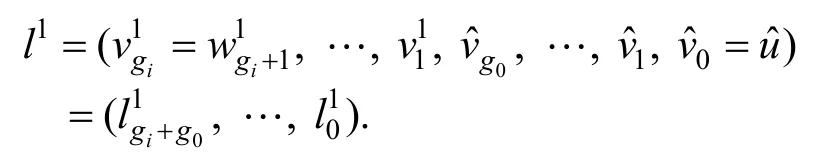
且由于δ∊S,所以有如下不等式关系:
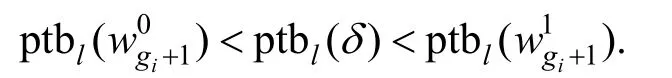
下面将讨论: 在事件B发生的前提下,事件C发生的概率。
若δ∉ S ⋀ t ype= 0 ,令 i = d eep(δ) - 2 ,则算法B伪 造 的 证 据 为 w = ( (b1,… ,bgi+g0),(wgi+g0,… ,w1) ),然后通过累加器生成算法可以获得树T中的一条路径:


综上可以得出事件C发生的概率:

该结果与哈希函数Ha的抗碰撞性定义相矛盾。根据定理6可以得知当存在PPT算法打破哈希函数Ha的抗碰撞性,也能找到一个PPT算法打破问题的困难性假设。
4 零知识证明
本节主要介绍Ring-SIS通用累加器相关的,被累加值的零知识证明协议П。在此之前,首先简要介绍协议中主要用到的一些技巧以及协议所证断言的变形过程。
4.1 秘密值之间特殊关系证明

则可以从等式组
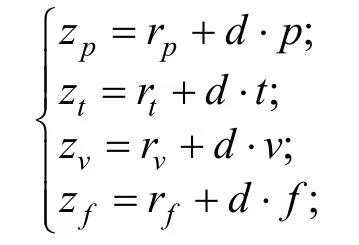
中获得如下关于d的线性关系式:
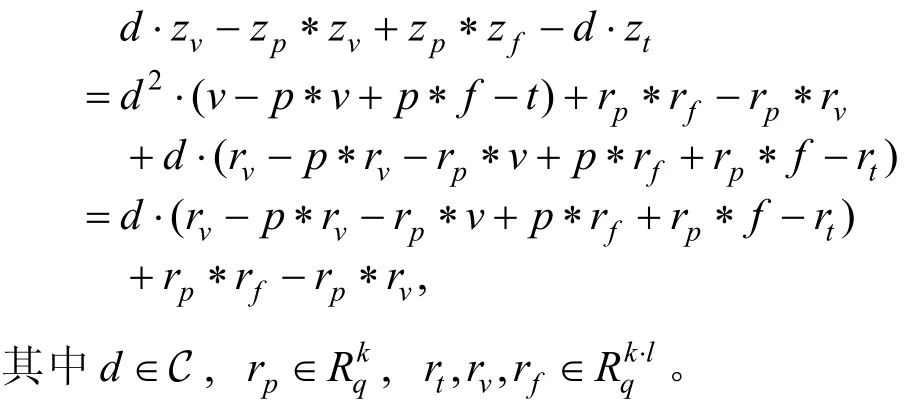
为了证明秘密值p,t,v,f之间形如:

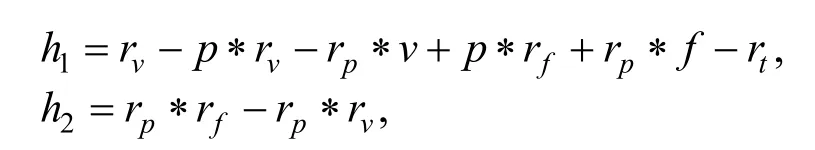
然后计算 c1= C om(h1)与 c2= C om(h2),并将其先发送给验证者。证明者在收到挑战值后,再计算并回复消息 zb,zf,zt给验证者,最后由验证者验证:
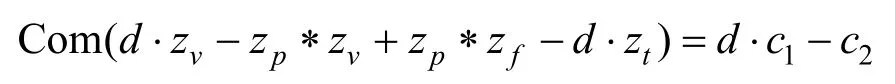
是否成立。
4.2 范围证明
为了证明秘密满足一些特殊的范围限制,通常会采用范围限制转换技术来实现,范围限制转换技术即将秘密值满足范围限制这一条件转换成秘密值满足特定关系等式的条件。比如,为了证明秘密值,则只要证明等式是否成立即可,另外,集合{0,1}k可以看做是kR的真子集。
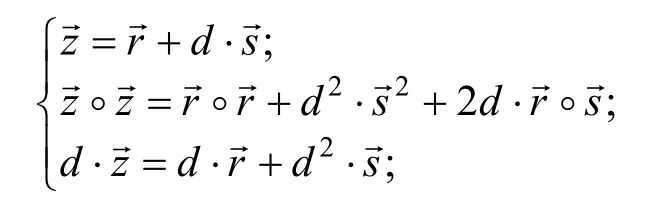
中,推导出
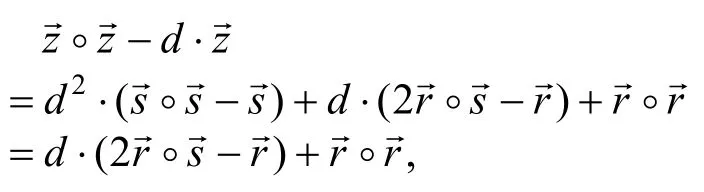
最终得到了一个关于d的线性关系式。

是否成立即可。
4.3 被累加值的零知识证明
本小节将详细介绍如何使用秘密值的特殊关系证明以及范围证明等技巧来共同实现 Ring-SIS通用累加器所对应的,被累加值的零知识证明系统。该零知识系统具体可以表述成如下语言:

根据 3.2小节中的成员关系验证算法的要求,当hg+r= δ ,对∀j∊[L],有下列等式成立:
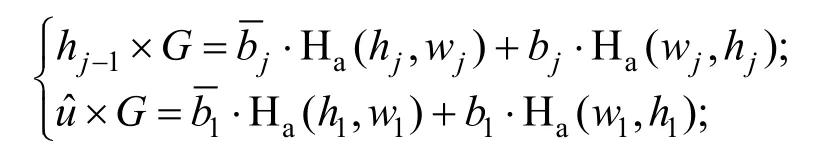
上述等式也得能等价于如下形式:
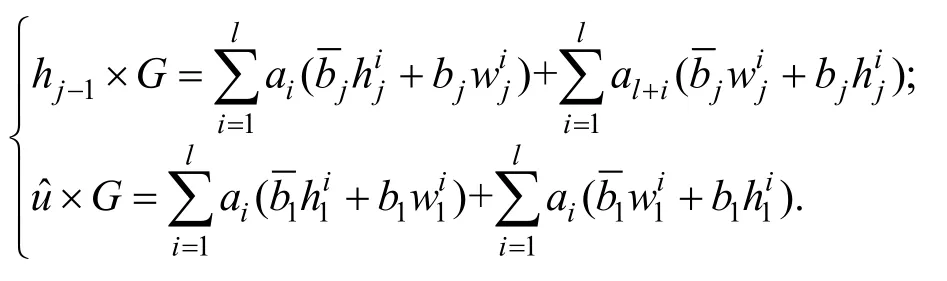
为了更加简洁地描述上述验证等式,我们可以定义如下参数符号:
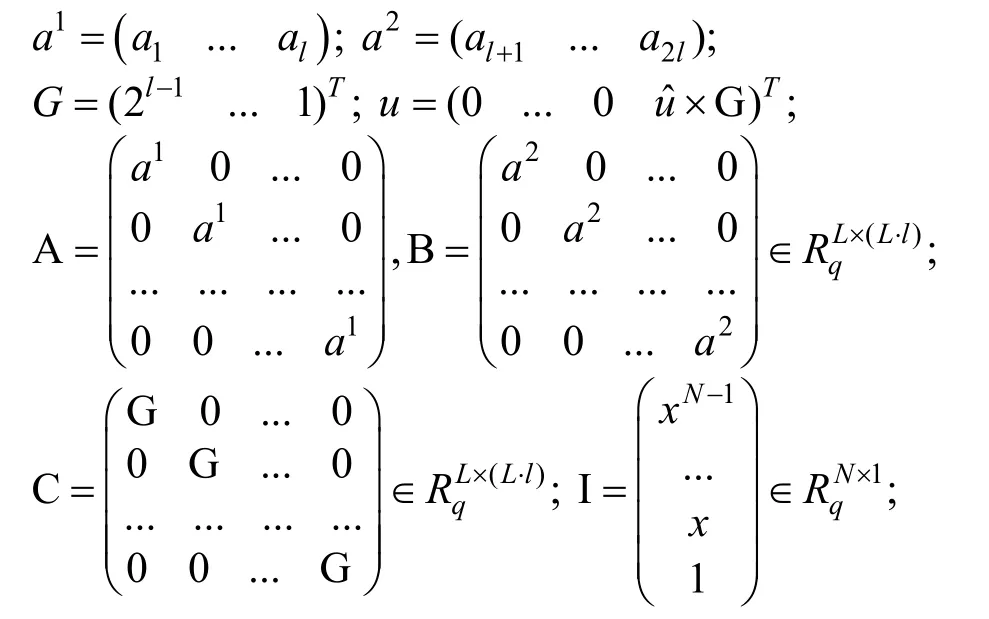
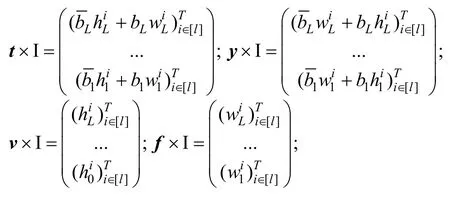
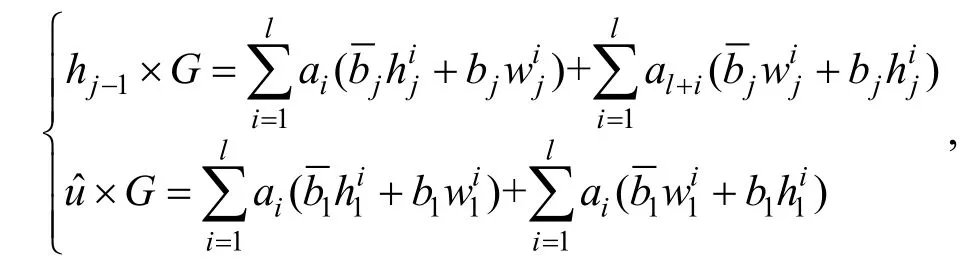
可以得到简洁版的成员关系验证等式:

下面将构造被累加值的零知识证明协议П来零知识地证明秘密值满足上述成员关系验证等式。
协议П:
公共输入:
输入证据:
证明目标:存在向量满足下述关系:
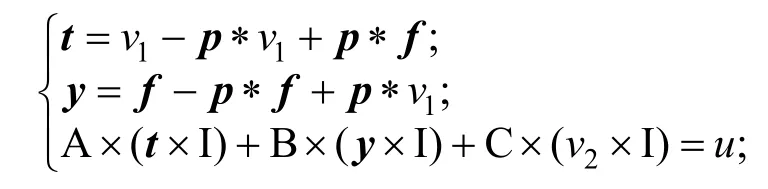
生成证明:
(1) 证明者选择以下随机数:
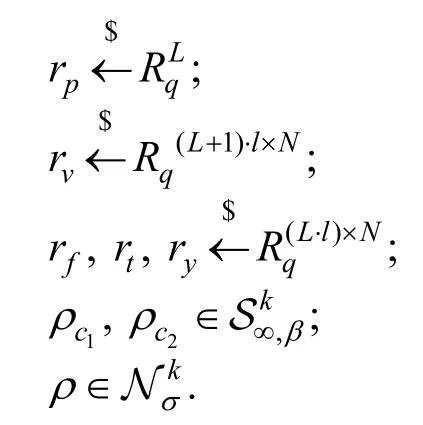
定义如下参数:

计算
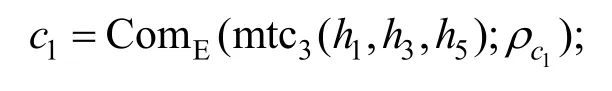
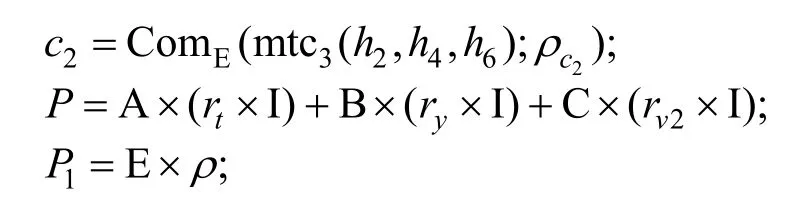
最后证明者将消息
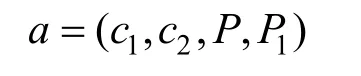
发送给验证者。
(3) 证明者检查挑战d是否有效,若有效则计算如下消息:


(4) 验证者令
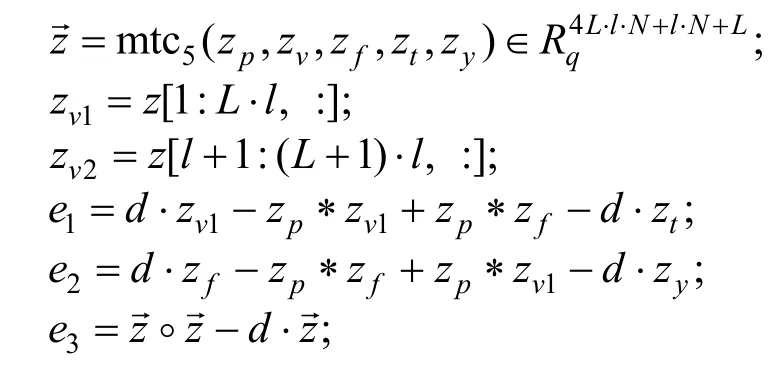
并检查下述条件:

是否都成立。
4.4 安全性分析
完整性:当协议不中止,诚实证明者可以正确回复所有来自验证者的挑战d,由定理2可知,当σ=α∙T ,可以获得 M =exp(12/α + 1 /(2α2) ),协议中断的概率。另外根据定理1可知因此诚实证明者使得诚实验证者相信的概率趋近于
3-特殊合理性:当恶意证明者能以的概率猜中挑战值,或者能以不超过τ的概率伪造承诺并通过验证,则合理性错误 e rrors最多为。将概率τ降至,则协议的合理性错误为
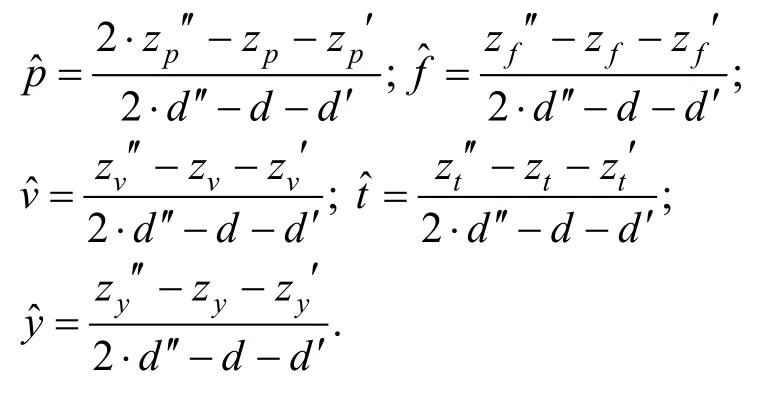
接下来证明提取出的秘密具有合法有效性。令
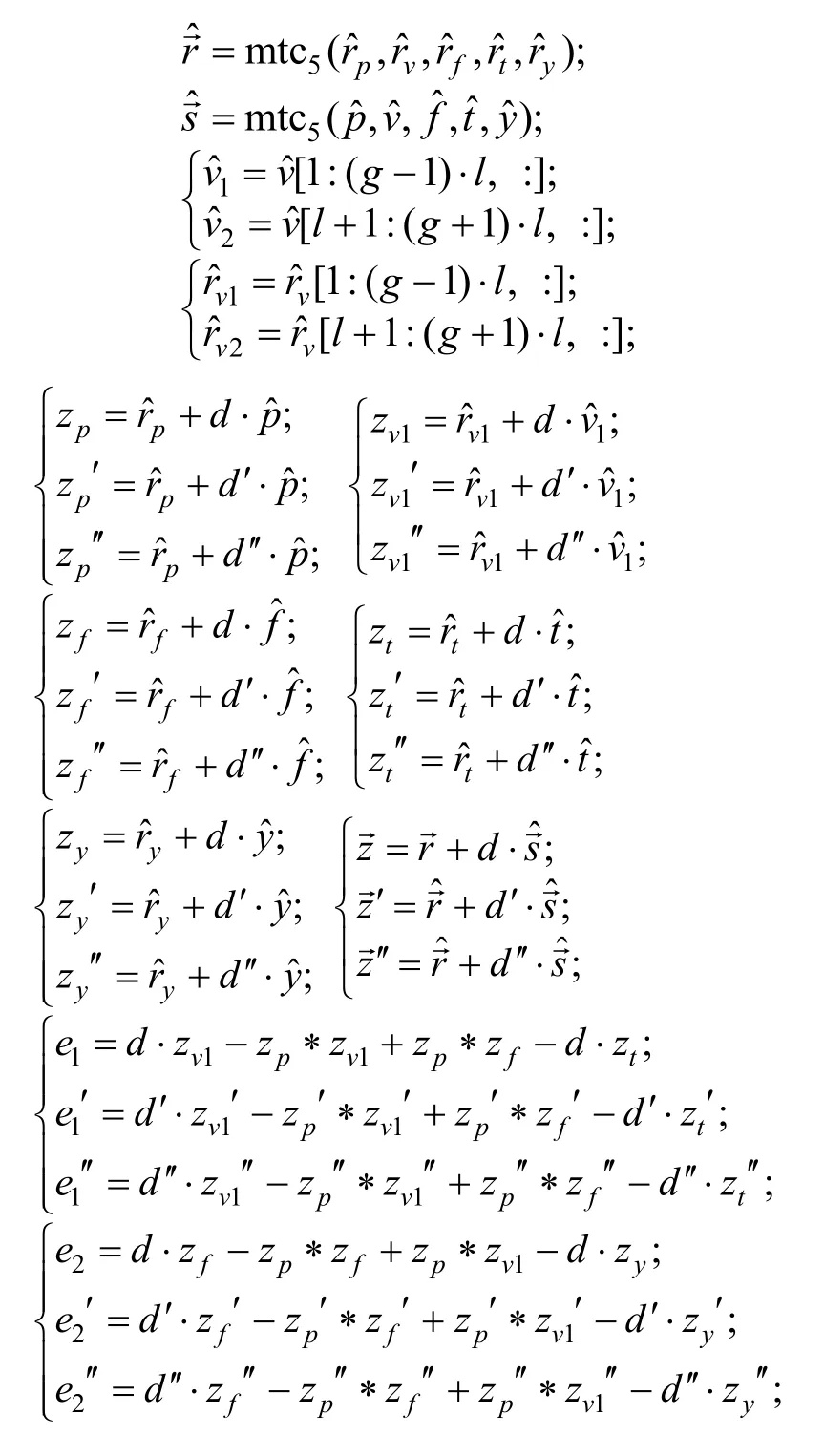
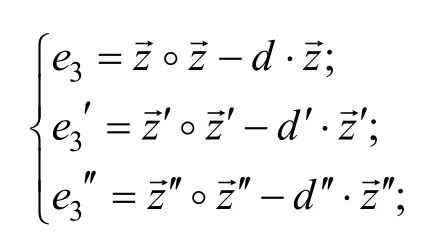
对于验证公式:

可以推导出:

由于 d '- d≠ 0 ,且根据定理 4可知,d'-d在Rq中是可逆的,所以可以得出结论:
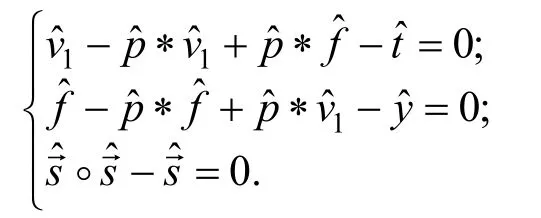
另外根据验证等式:
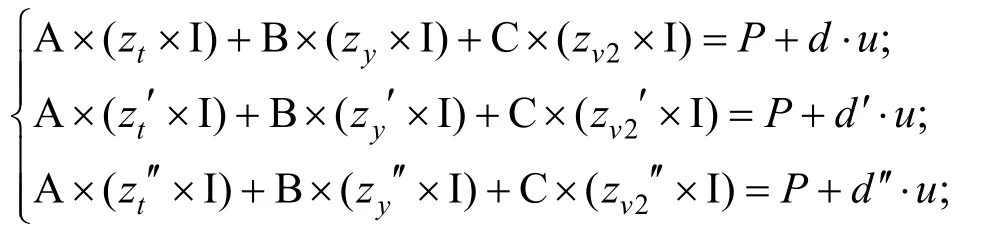
可以推导出
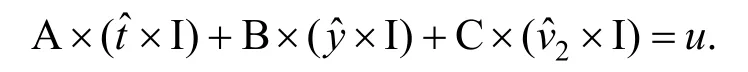
诚实验证者零知识性:
模拟器Sim:
(1) 随机选择

(3) 以概率 Pabort= 1 - 1 /M输出副本:
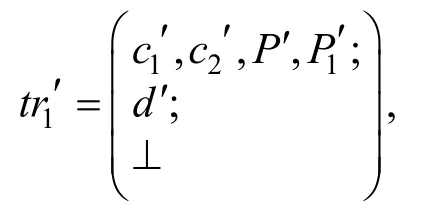
并中止程序,否则继续步骤4;
(4) 随机选择

(5) 令

(6) 计算
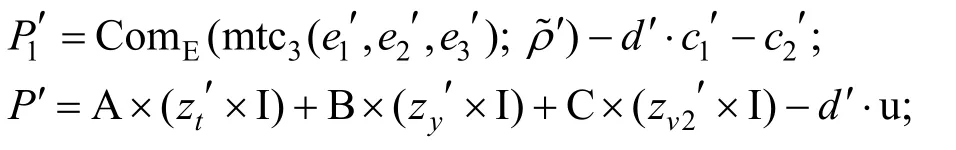
(7) 以概率 Pabort= 1 - 1 /M 输出副本:
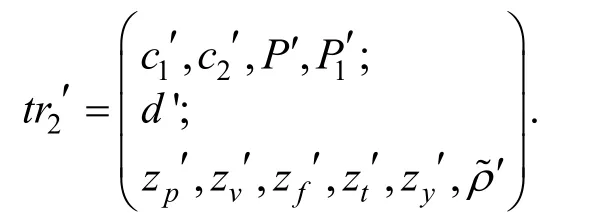
下面将论证模拟器Sim输出副本的分布与协议П输出副本的分布不可区分。
在模拟器Sim被中止的情况下,由于承诺方案的隐藏性,所以(c1,c2)的分布与的分布不可区分; P1与都来自于相同分布; P的分布由来自于均匀随机分布的 rt,ry,rv共同决定,所以P与P′也是不可区分的。故而在被中止情况下,副本′的分布与协议П输出副本的分布是不可区分的。
在模拟器Sim不被中止的情况下,承诺值(c1,c2)的分布与的分布不可区分依赖于承诺方案Com的隐藏性; 由于协议П在不中止的情况下,有效副本需要满足的条件,又因为因此,当问题对于任意算法是困难的,P的分布与上均匀随机1分布不可区分,所以的分布与′的分布也是不可区分的,具体可参考文献[18]定理 6中的证明; 对于P的分布与P′的分布,由于′都是均匀随机抽取的,所以P与P′的分布也是均匀随机的; 对于(zp,zv,zf,zt,zy)的分布,又由于rp,rv,rf,rt,ry都分别取自均匀随机分布,所以(zp,zv,zf,zt,zy)的分布与的 分布也是不可区分的; 最后根据定理2可知,由拒绝抽样所得的的分布与是统计不可区分的。
故综上,模拟器Sim输出副本的分布与协议П输出副本的分布是不可区分的。
4.5 拓展
关于基于 Ring-SIS的通用累加器所对应的非被累加值的零知识证明系统,具体可以表述成如下语言:

根据3.2小节中的非成员关系验证算法,非被累加值的零知识证明需要证明者证明非被累加值所在子树中存在两个相邻叶子节点,且非被累加值的大小在这两个叶子节点取值之间,为了实现以上过程,不仅需要被累加值的零知识证明,还需要大整数范围证明以及大整数加法关系证明共同实现。由于基于Schnorr-like框架的大整数间加法关系的零知识证明还未取得相关进展,故暂时未能实现对于合理性错误可忽略的非被累加值的零知识证明,我们未来也将继续探究该问题。
5 总结
近年来,各类抗量子的密码学工具逐渐走入人们的视野,其最大的亮点主要在于更强的安全性,但影响着其实用性的关键主要还是在于其效率的考量。本课题主要是从抗量子攻击通用累加器的效率角度,以及相应知识的零知识协议的效率角度进行进行研究,提出了计算效率和更新效率远优于以往方案的 Ring-SIS通用累加器,同时还提出了单轮次执行合理性错误可忽略的,被累加值的零知识协议方案,其直接解决了以往方案需要重复执行多次来降低合理性错误的弊端,为基于格上困难性假设的通用累加器实用性相关的研究,进行了近一步的探索。

