密码累加器研究进展及应用
苗美霞,武盼汝,王贇玲
(西安邮电大学 网络空间安全学院,陕西 西安 710121)
密码累加器能够高效地证明元素是否存在于集合中。具体来讲,首先将集合X={x1,…,xn}中的所有元素累加到累加器accX中,然后计算元素xi∈X的证据wi,最后利用证据wi和累加值accX来证明元素xi∈X。密码累加器与向量承诺[1-2]、零知识集合(ZK-sets)[3-4]等原语有紧密的联系,三者都能解决(非)成员验证的问题。但是,三者在验证内容、隐私性等方面存在一定的区别。向量承诺[1-2]针对有序集合(向量) 提供验证,即不仅能够证明元素mi存在于有序集合中,而且能证明mi是第i个位置上的消息,但是其计算复杂性较大。零知识集合[3-4]不仅能够证明某个元素是否属于集合,同时不泄漏任何关于集合的信息,如集合的大小。然而,零知识集合的验证开销与集合中元素的数量线性相关,效率较低。
BENALOH等[5]于1993年首次提出密码累加器的概念,但是该构造为静态累加器,即累加集合固定不变。CAMENISCH等[6]于2002年提出了动态累加器的概念,可以支持累加集合动态地添加和删除元素。然而,上述两类累加器仅支持集合中元素的成员证明,即xi∈X,而无法支持非成员证明,即无法提供y∉X的证据。为了解决此问题,LI等[7]于2007年首次提出了通用累加器的构造,能够同时实现成员和非成员证明。
密码累加器自提出以来,许多学者对其进行了大量的研究并给出了具体的构造方案。基于不同的密码工具,密码累加器可分为基于RSA体制的累加器[5-8]、基于双线性映射的累加器[9-12]和基于Merkle哈希树的累加器[13]。密码累加器有着广泛的应用场景。在访问控制系统中,将授权用户的访问权限聚合到累加器中,授权用户通过将成员证据作为访问凭证来访问系统。在匿名凭证系统中[6],需要进一步隐藏用户的身份,将累加器和零知识证明[14]结合是解决这类问题的有效方法。在数据外包存储中,密码累加器可用作认证数据结构(Authenticated Data Structure,ADS)[15-18],用户利用计算结果和相应证据来证明计算结果的正确性。在加密货币中,密码累加器通过代替Merkle哈希树来降低通信开销和提高验证效率[19]。此外,累加器还可应用于时间戳[5]、隐私保护数据外包[20]、认证字典[21]、编辑[22]、负责任的证书管理[23-24]等场景中。
笔者首先从密码累加器的构造方案和功能应用等方面对现有方案进行了分类、分析和总结;其次介绍了密码累加器的主要应用场景;最后指出了现有方案面临的一些问题以及未来的发展趋势和研究方向。
1 累加器模型与定义
1.1 系统模型
一般来讲,一个密码累加器主要包括以下3个主体。
(1) 累加器管理员:生成密钥对,创建并发布累加器。此外,动态累加器可以添加和删除元素,并创建这些元素的成员证据。通用累加器可以对没有被聚合到累加器中的元素创建非成员证据。
(2) 用户:接受累加器管理员提供的证据,证据是他们在累加器系统中的凭证,可以提供给验证方进行验证。之后有新的元素添加到累加器时,用户可以在本地更新证据。
(3) 验证方:通过用户提供的证据和累加器公开的累加值,来检查元素x是否在此累加器中。
下面分别对静态累加器、动态累加器以及通用累加器进行了定义。用X表示累加器的累加值域,用X={x1,…,xn}表示累加器中元素的集合,用t表示累加元素的上限,t可以是无穷的,表示累加域无界。此外,陷门信息(即私钥skacc)是可选择的输入,因为有些累加器需要陷门信息才能更新累加器或证据,而有些不需要。
定义1一个静态累加器方案可以描述成一个四元组Π=(Gen,Eval,WitCreate,Ver)。
(1) Gen(1λ,t):累加器管理员输入安全参数λ、累加元素上限t,输出密钥对(skacc,pkacc),如果累加器不存在陷门信息,则陷门信息skacc=φ。
(2) Eval((skacc,pkacc),X):累加器管理员计算累加值和辅助信息。输入集合、密钥对(skacc,pkacc),输出累加值accX,并将其公布给用户和验证方;输出辅助信息aux,并发送给用户,使得用户可以在本地更新证据。
(3) WitCreate((skacc,pkacc),xi,accX,aux):累加器管理员创建用户xi的证据。输入密钥对(skacc,pkacc)、累加值accX、元素xi∈X及辅助信息aux,生成xi的证据wi。
(4) Ver(pkacc,xi,wi,accX):验证方验证元素是否在累加器中。输入公钥pkacc、累加值accX、元素xi及其证据wi。如果wi是xi∈X的证据,则返回1;否则,返回0。
在此基础上,如果累加器可以动态地更新集合X,并可以有效地更新集合中元素的证据,那么该累加器为动态累加器。通过对静态累加器定义扩展,可以得到一个动态累加器。
定义2动态累加器在静态累加器的基础上添加了一个三元组Π=(Add,Del,MemWitUp)。
(1) Add((skacc,pkacc),accX,aux,x):累加器管理员添加元素x∉X到累加器中,并更新累加值accX。输入密钥对(skacc,pkacc)、累加值accX、辅助信息aux和要添加的元素x∉X,输出更新后的累加值accX′=accX∪{x},并更新辅助信息aux。
(2) Del((skacc,pkacc),accX,x,aux):累加器管理员删除元素x∈X时,更新累加值accX。输入密钥对(skacc,pkacc)、累加值accX、辅助信息aux和被删除的元素x∈X,输出更新后的累加值accX′=accX{x},并更新辅助信息aux。
(3) MemWitUp((skacc,pkacc),x,wi,aux):添加或删除元素x后,用户更新元素xi的证据wi。输入密钥对(skacc,pkacc)、x、辅助信息aux和xi的证据wi,输出xi更新后的证据w′i。
上述累加器可以对元素x∈X构造成员证据,但无法对元素x∉X构造非成员证据。而通用累加器既可以对元素x∈X构造成员证据,又可以对元素x∉X构造非成员证据。
定义3通用累加器在上述WitCreate算法中,可以添加一个布尔参数type,创建成员证据时type=0,创建非成员证据时type=1。如果通用累加器不具备动态累加器添加或删除元素的功能,则为通用静态累加器,否则为通用动态累加器。对于通用动态累加器,则需要在定义1和定义2的基础上添加NonMemWitUp算法,可以在累加集合更新时,对非成员证据进行更新。
(1) NonMemWitUp((skacc,pkacc),x,w,aux):在添加或删除某个元素x时,用户更新非成员元素y∉X的证据u为u′。输入密钥对(skacc,pkacc)、x、辅助信息aux和y的证据u,输出y更新后的证据u′。
1.2 累加器的性质
累加器有3个安全性质:正确性、健壮性(包括无碰撞性和不可否认性)、不可区分性。3个安全性质定义如下:
(1) 正确性:对于所有诚实生成的密钥、所有诚实计算的累加值和证据,验证算法Ver将始终返回1。
(2) 健壮性:传统上,健壮性指无碰撞性,对于元素y∉X,很难找到其成员证据[8],对于元素xi∈X,也很难找到其非成员证据[7];健壮性的另一种扩展形式是不可否认性[23],不可否认性是通用累加器特有的性质,它表示为元素x∈X或x∉X计算两个相互矛盾的证据在计算上是不可能的。
(3) 不可区分性:不可区分性[25-26]与安全隐私相关,指累加器和持有证据的用户都不会泄露有关累加集合X的信息。
分别对静态累加器、动态累加器和通用累加器进行形式化定义。具体如下:
(1) 安全性(静态):一个静态累加器是安全的,如果对于所有概率多项式时间(Probabilistic Polynomial Time,PPT)对手Aλ,有
(2) 安全性(动态):令M为接收输入(f,aux,g)的交互式图灵机,其中,aux是有关f的辅助信息,g∈ZA。M维护一个元素集合X,该集合最初为空,初始累加器acc设置为g。M响应两种消息:对于消息D(add,x),它确保x∈X,将x添加到集合X中,通过运行D修改acc,然后将更新后的acc发回;对于消息D(delete,x),它将检查x∈X,将其从集合X中删除,通过运行D更新acc,然后将更新后的acc发回。最后,M输出X和acc的当前值。如果对于所有PPT的对手Aλ,动态通用累加器方案是安全的,则有
(3) 安全性(通用):一个通用累加器是安全的,如果对于所有PPT对手Aλ,有
2 基于RSA体制的累加器
2.1 静态累加器
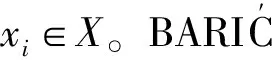
(1) Gen(1λ):累加器管理员输入安全参数λ,生成累加器初始值g∈Zn,输出密钥对(skacc,pkacc)=((p,q),N),其中N由两个大的强素数p、q组成,且N=pq。
(2) Eval(pkacc,X):累加器管理员计算累加值。累加值accX=gx1,…,xnmodN,其中X={x1,…,xn},且xi是素数。
(3) WitCreate(pkacc,xi,accX):累加器管理员创建用户的证据。输入公钥pkacc、累加值accX和元素xi,生成xi的证据wi=gx1,…,xi-1,xi+1,…,xnmodN。
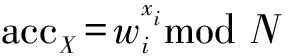
值得注意的是,RSA累加器在计算过程中需要进行模幂运算,集合X中的元素在指数中是乘法关系,所以上述构造的元素必须限制为素数,如果聚合的是非素数,则可能存在某个值是另2个值的乘积,进而敌手可以很容易伪造证据进行验证。
2.2 动态累加器
在一些需要添加或撤销成员的应用场景中,如在群签名、匿名凭证撤销系统中,群管理员需要动态添加或撤销成员资格。然而,上述静态累加器的集合元素固定,不具备添加或删除的功能。因此,CAMENISCH等[6]为了解决匿名凭证系统的撤销等问题,将累加器扩展为动态。动态累加器允许累加器管理员动态地添加或删除元素,并且可以动态地更新累加器和成员证据。在添加元素时,更新累加器、成员证据只需要进行简单的模指运算,可以很容易实现;而在删除元素时,CAMENISCH等[6]采用了RSA算法的基本思想来更新累加器,通过使用陷门信息skacc进行求逆运算,可以将元素从累加器中删除。删除元素时需要用陷门信息更新累加值,但更新成员证据时无需陷门信息。方案具体如下:
(1) Gen(1λ):累加器管理员生成公私钥对,初始空累加值acc0=g∈ZN。输入安全参数1λ,输出累加器管理员公私钥对(skacc,pkacc)=((p,q),N),其中N=pq,且p、q为大的强素数。
(2) Add(accX,x,X,pkacc):累加器管理员添加元素x后更新累加值accX。添加元素x∉X到累加器中,X更新为X∪{x},更新后的累加值为
(3) Del(accX,x,X,(skacc,pkacc)):累加器管理员删除元素x后更新累加值accX。删除元素x时,需要陷门信息skacc,通过计算的累加值为
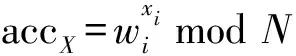
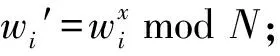
值得注意的是,执行删除操作时,累加器管理员需要用到陷门信息skacc来更新累加值,此时不诚实的累加器管理员可以通过陷门信息随意更改累加值、对成员创建假的证据等,所以必须要求累加器管理员是可信的。
2.3 通用累加器
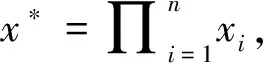
该方案给出了两种创建非成员证据的方法,一种需要陷门信息skacc,另一种不需要。不需要陷门信息的方法在计算非成员证据时需要找到a、b,使得ax*+byi=1,而x*与累加器成员个数线性相关,计算开销很大。需要陷门信息的方法在计算证据时,可通过x*′=x*mod(p-1)(q-1),其中p、q为陷门信息,使得x*′在进行模运算后很小,从而在ax*′+byi=1中,证据的计算开销仅为O(1)。因此在某些可以使用陷门信息的场景下,选择需要陷门信息计算非成员证据的计算量小;而对于某些无法使用陷门信息的场景下,不需要陷门信息计算非成员证据是一个很好的选择。下面给出了两种计算非成员证据的具体构造。
2.3.1 需要陷门信息
使用skacc计算非成员证据。假设存在受信任的累加器管理员知道skacc=(p,q)、集合X={x1,…,xn}、累加器accX=gx1,…,xnmodN,其中g∈QRN。累加器管理员计算元素yi∉X的非成员证据如下:
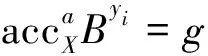
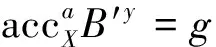
2.3.2 不需要陷门信息
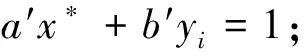
该方案同时支持元素的动态添加和删除,并实现相应证据的高效更新,具体的非成员证据更新算法NonMemWitUp如下:
NonMemWitUp(x,(a,B),accX,accX′):
添加:添加元素x∈XX,且x≠yi,给定更新前后的累加器accX和accX′,则yi∈XX的证据ui=(a,B)更新如下:
(1) 找到两个整数a0′和r0,使得a0′x+r0yi=1,由于x、yi都为素数,所以a0′、r0可以很容易找到;
(2) 两边同乘更新前的证据a,使得a0′ax+r0ayi=a;
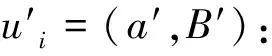
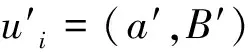
(1) 选择一个整数r,使得ax-ryi∈Z2l;
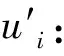
2.4 支持批处理更新的累加器
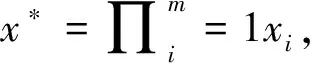
LI等[7]简要地概述了累加器可以批量添加和删除元素,并未给出具体的算法,而BONEH等[19]给出了具体的批量添加(BatchAdd)和批量删除(BatchDel)的算法。在BatchDel中,存在一个ShamirTrick算法,可以将两个元素的证据聚合在一起。具体的算法如下:
(1) BatchAdd(accX,{x1,…,xm})
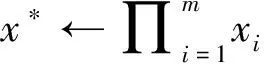
② accX′←accx*
(2) BatchDel(accX,(x1,w1)…(xm,wm))
① accX′←w1
②x*←x1
③ fori←2,i≤m
④ accX′←ShamirTrick(accX′,wi,x*,xi)
⑤x*←x*·xi
⑥ return accX′
(3) ShamirTrick(w1,w2,x1,x2)

②a,b←Bezout(x1,x2)
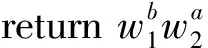
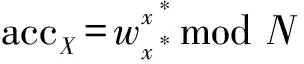
PoE协议输入:u、w∈G,x∈Z;证明:ux=w。
① 验证方发送随机的λ比特的素数l给证明方;
② 证明方计算(q,r),使得x=ql+r,并将Q=uq发送给验证方;
③ 验证方计算r=xmodl,当Qlur=w成立时接受。
此外,为了减小通信开销,BONEH等[19]也使用了Fiat-Shamir启发式方法[32]及多轮协议的概括[33],将PoE协议改成了非交互式协议NI-PoE。并将NI-PoE协议运用到累加器中来提高批处理成员验证的效率,具体构造如下:
MemWitCreate*(accX,{x1,…,xn})
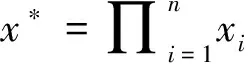
②wx*←WitCreate(accX,x*)
③ returnwx*,π=NI-PoE(x*,wx*,accX)
VerMem*(accX,{x1,…,xn},w={wx*,π})
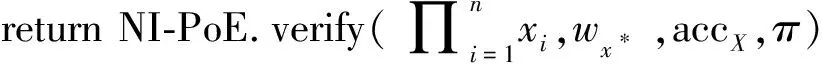
除了成员验证效率得到了提高,非成员验证的效率也提高了。当进行批处理非成员验证时,一种方法是通过NonMemWitCreate*算法将多个非成员元素直接相乘来创建证据,验证时只需要验证VerNonMem*算法中的协议运行是否成功。另一种方法是通过AggNonMemWit算法聚合这些非成员证据来创建证据。

PoKE2协议输入:u、w∈G;证据:x∈Z;证明:ux=w。
① 验证方发送g给证明方;
② 证明方发送z=gx给验证方;
③ 验证方发送随机的λ比特的素数l和一个挑战值α给证明方;
④ 证明方计算(q,r),使得x=ql+r,并将Q=uqgαq和r发送给验证方;
⑤ 验证方检查Qlurgαr=wzα是否成立。
NonMemWitCreate*(accX,x*,y*)://accX=gx*,x*=∏x∈Xx,y∈∏yi
①a,b←Bezout(x*,y*)//ax*+by*=1
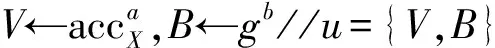
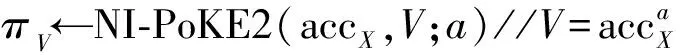
④πg←NI-PoE(y*,B,gV-1)//By*=gV-1
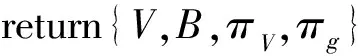
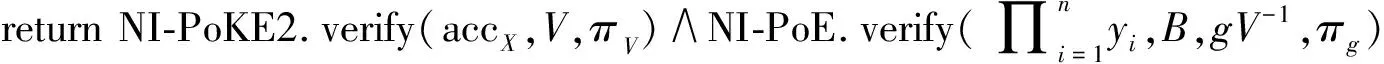
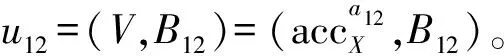
①a,b←Bezout(y1,y2)
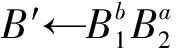
③a′←ba1y2+aa2y1
④a12←a′mody1y2
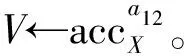
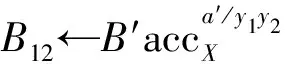

⑧πg←NI-PoE(y12,B12,gV-1)//By1212=gV-1,y12=y1y2,

3 基于双线性映射的累加器
RSA累加器方案中,累加器聚合的元素被限制为素数,需要把元素转变为素数[34]后才能进行累加。为了解决这个问题,NGUYEN等[9]首次提出了基于强Diffie-Hellman(SDH)假设的双线性映射动态累加器,此累加器不要求累加值域为素数。DAMGARD等[10]和AU等[11]补充了LI等[7]提出的通用累加器构造,使得双线性映射累加器同RSA累加器一样,都具备了动态和通用的功能。然而,上述累加器中累加集合的大小需提前设定,如累加的元素数量上限为q。因此,TOLGA等[35]通过一组累加器突破了上述累加集合大小受限的问题。此外,CAMENISCH等[12]也给出了一种基于q-DHE假设的方案,此方案对证据和累加器的更新无需陷门参与,即支持公开更新。
3.1 动态累加器
RSA累加器的累加域元素要求为素数,为了解决这一问题,NGUYEN等[9]提出了基于q-SDH假设的双线性映射累加器,其中累加的元素的数量上限为q。相比于RSA累加器采用模幂运算聚合累加元素,此构造以双线性对运算为基础。具体构造如下:
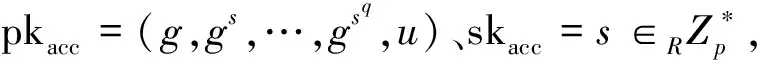
(2) Eval(X,pkacc):累加器管理员计算累加值accX。输入集合X={x1,…,xn}⊂Zp{-s},其中n≤q,使用pkacc而无需私钥s的情况下计算累加器accX=gu∏x∈X(x+s)。
(3) WitCreate(pkacc,xi,accX,X):累加器管理员创建用户xi的证据。输入公钥pkacc、累加值accX、集合X和元素xi,生成xi∈X的证据为wi=gu∏x∈X{xi}(x+s)。
(4) VerMem(accX,xi,wi):验证方验证xi是否在累加器中。通过验证e(wi,gxigs)=e(accX,g)是否成立。如果成立,则输出1,否则输出0。

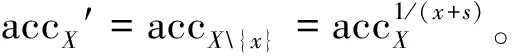
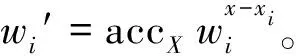
要注意的是,在上述构造中,公钥大小与累加元素的上限q线性相关,如果q很大,则元素公钥将会非常大,而在RSA累加器中,公钥是常数N。此外,RSA动态累加器只有在删除操作更新累加值时会用到陷门信息skacc,而在此构造中,更新累加值时,包括添加和删除都需要用到陷门信息。
双线性映射动态累加器除了该基于q-SDH假设的方案之外,CAMENISCH等[12]也给出了一种基于q-DHE假设的构造。此方案采用了两个公开的集合V和Vw,分别是被累加到累加器中的元素集合和证据wi被创建时,累加器添加或删除了哪些元素的集合。当证据需要更新时,可以通过Vw对所有元素的证据公开更新。具体构造如下:
(1) Gen(1λ,t):输入参数1λ和累加元素上限t,累加器管理员随机选择值γ∈Zq,生成初始累加器accφ=1、初始状态stateφ=(φ,gγ1,…,gγq,gγq+2,…,gγ2q)和公私钥对:
(pkacc,skacc)=((g1,…,gq,gq+2,…,g2q,e(g,g)γq+1,pksig),(γ,sksig))=
((gγ1,…,gγq,gγq+2,…,gγ2q,e(g,g)γq+1,pksig),(γ,sksig)) 。
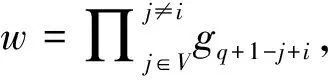
stateU∪{i}={U∪{i},g1,…,gn,gn+2,…,g2n} 。
(3) Update(pkacc,V,stateU):用户输出accV=∏v∈Vgn+1-v(V⊂U)。
(4) WitUp(pkacc,wi,Vw,V,accV,stateU):任何不可信实体都可以进行证据的更新。如果i∈V且V∪Vw⊂U,计算
输出wi′=(w′,σi,gi)。
(5) VerMem(pkacc,i,wi,accV):验证方验证i是否在累加器中。不可信实体更新证据wi后,用户i获得新的证据wi′后,通过等式e(gi,accV)=ze(g,w)来验证i是否在累加器中。
在删除成员时,RSA累加器[6-7]和基于SDH假设的双线性映射累加器[9-10]更新累加值都会用到陷门信息,并且更新操作都进行了幂运算。而该方案在删除成员时更新累加器不需要陷门信息,并且更新操作无需进行幂运算,只用进行简单的乘法运算,因此计算效率大大提升。
3.2 通用累加器
上述累加器无法支持非成员验证,因此,DAMGARD等[10]首次基于SDH假设将双线性映射累加器扩展为通用累加器,具体非成员证据的构造和验证方法如下:

(2) VerNonMem(accX,y,(ay,By)):验证方验证元素y的非成员身份。已知公共参数gs,验证通过检查e(ay,gygs)=e(accXgBy,g)是否成立。如果成立,则输出1,否则输出0。
在该方案的基础上,AU等[11]也提出了基于SDH假设的通用累加器方案,使得无需使用陷门信息便可进行累加器的更新。
4 基于Merkle哈希树的累加器
Merkle哈希树累加器是一类设计简洁且高效的累加器。Merkle哈希树中,叶子节点为集合元素的哈希值,内部节点为左右孩子的哈希值,根节点为最终累加值。元素xi的成员证据由xi到根节点路径上的所有兄弟节点组成,通过重构根节点来判断元素xi是否存在于集合中。然而,RSA累加器和双线性映射累加器只需O(1)大小的证据,而Merkle哈希树累加器需要O(logN)大小的证据,其中N表示累加元素的总数。
CAMACHO等[13]给出了一个通用累加器方案的简单构造,该方案和LI等[7]的通用累加器方案在功能上是相似的,适用于动态集合并允许非成员身份证明,并且该方案在存在抗碰撞哈希函数的假设下可证明是安全的。该方案实现非成员证明的主要思想为:集合中元素按顺序存储,若某元素的左右相邻元素为连续元素,则该元素不在集合中。例如,x的左右相邻元素为xα、xβ,且xα、xβ连续,则x为非成员元素。方案具体构造如下:
(1) Gen(1λ):累加器管理员输入安全参数λ,生成初始累加器acc0和M0。初始集合X为空,是M={0,1}λ的子集;然后选择一个哈希函数H,计算一个随机索引i∈K,并设置H=Hi;最后将m的初始值设置为H(-∞‖+∞)的根节点Nm,并且累加器管理员公布acc0=ProofNm。
(2) WitCreate(m,x):累加器管理员创建证据。输入x∈M和内存m,计算证据w=(w1,w2)如下:
① 如果x∈X,则证据w1=(xα,xβ),其中x=xα或x=xβ;否则x∉X,证据w1=(xα,xβ),其中xα ② 设置w2是由H(xα‖xβ)生成的m的最小子树。 (3) Update(m,x):累加器管理员更新累加器、内存m和证据w。输入x∈X,acc和m。 ① 添加:x∉X时,添加x操作如下:将m中适当节点处的值H(xα‖xβ)替换为H(xα‖x),其中xα ② 删除:删除x时,查找包含x的两个节点,用Vα,Vβ表示。删除x后,用H(xα‖xβ)代替之前的H(xα‖x)和H(x‖xβ),并保持树平衡。更新后的树为m′、累加器acc′=Proofm′、证据w′=(del,w1,w2,w3)。 (4) CheckUpdate(acc,acc′,w′):在添加或删除元素后,用户检查累加器管理员提供的更新后的元素,更新正确,则输出OK。输入x∈M、更新前的累加器acc、更新后的累加器acc′和更新后的证据w′。如果w′=(add,w1,w2)且符合下列前提,则算法输出1;否则输出0。删除操作也类似,这里省略。 ①w1是通过在w2上添加叶子获得的树。 ② 除了值是H(xα‖xβ)的节点以外,w1、w2树中其余所有节点都相同。 ③ Proofw1=acc,Proofw2=acc′。 ④H(xα‖x),H(x‖xβ)∈Vw2。 (5) VerMem(x,w,acc):验证方验证某个元素是否在集合中。输入x∈M、证据w=((w1,w2),u)和累加器acc。检查(a)Proofu=acc;(b)H(x′‖x″)∈Vu和(c)(x=x′),(c)(x=x″)或(c′)(x′ 首先,在RSA累加器和双线性映射累加器中,需要累加器管理员生成陷门信息来更新累加器或证据,而Merkle哈希树累加器[13]不需要陷门信息来更新累加器或证据,因而无需管理员参与。其次,Merkle哈希树累加器主要基于哈希算法,而RSA累加器和双线性映射累加器分别需要模指数运算和双线性对运算,所以Merkle哈希树累加器计算效率高。然而,Merkle哈希树累加器的证据大小与集合大小呈对数关系,所以通信代价较高。 对上述3类密码累加器的构造方案进行了比较和总结。RSA累加器基于强RSA假设,具有较短的公共参数,且可以很容易扩展到通用累加器[7]或动态累加器[6],但此类型下的累加器通常需要昂贵的操作才能将元素以素数形式编码。双线性映射累加器有基于q-SDH假设和q-DHE假设的两种类型,它们不需要素数编码,但需要最大元素数量的公共参数。大多数RSA累加器和双线性映射累加器都需要可信累加器管理员生成陷门信息。如在RSA累加器中,任何知道模N=pq分解的对手都可以轻易地作弊。而Merkle哈希树累加器不需要陷门信息,把这类不需要陷门信息的累加器也称为强累加器。Merkle哈希树累加器基于抗碰撞的哈希函数假设,是一类高效简洁的累加器,但是该类构造不需要可信的累加器管理员,所以需要O(logN)大小的证据(N表示累加集合的元素数量),而前两类需要可信设置的累加器只需O(1)大小的证据。此外,RSA累加器和双线性映射累加器也有一些构造[23,28]。这些构造下,累加器管理员完全不受信任,但这些构造要么证据数量随集合X的大小呈对数增长,要么依赖尚未在密码学进行深入研究的代数群。 表1给出了3类密码累加器构造方案的详细比较[26,36]。其中,S代表静态累加器,D代表动态累加器,U代表通用累加器,w代表成员证据的更新,u代表非成员证据的更新,a和d分别代表添加和删除操作时累加值的更新,acc代表累加值的更新,B代表累加器累加元素是否具有上限,|pkacc|、|w|、|u|分别代表公共参数,成员证据和非成员证据的大小。 表1 不同类型累加器的比较 累加器自提出以来,有着广泛的应用场景。包括时间戳[5]、群签名[6,37]、环签名[38]、访问控制系统[39]、匿名凭证系统[6]、加密货币[19]、认证数据结构(ADS)[15-18]等。此外,还被用在隐私保护数据外包[20]、认证字典[21]、编辑[22]、负责任的证书管理[23-24]等应用中。介绍几种典型应用:累加器在时间戳、成员资格撤销中的应用。此外,还会介绍最近比较流行的应用:累加器在区块链[40-42]中的应用。 BENALOH等[5]首次提出了密码学累加器,并应用于时间戳中。时间戳可以在任何文档上附加一个“发布”日期,以证明原始文件在签名时间之前已经存在。在传统的时间戳系统中,机构需要对文件逐个添加时间戳,验证方也需要逐个验证,使得时间戳的生成和验证代价高。为了提高时间戳系统的效率,BENALOH等[5]设计了基于密码累加器的时间戳系统,该系统可以批量的生成和验证时间戳。具体方法为:将某个时刻产生的所有文档聚合到累加器中,然后对该累加器附加时间戳。验证t时刻的文档时,仅需验证该文档存在于t时刻的累加器中,并且可以实现多个文档时间戳的批量验证,大大提高了时间戳系统的生成和验证效率。 静态累加器[5]可以用来解决时间戳、成员资格测试等集合成员无需变动的问题。然而,存在一些应用场景需要对成员进行添加或删除操作,如匿名凭证撤销系统、群签名方案、身份托管方案等[43-45]会进行撤销成员的操作。传统的撤销方案[43]如下:一种是当用户尝试访问资源时,验证方通过在数据库中查找用户的证书,使得证书被撤销的用户无法访问资源,但此查询操作与用户数线性相关;另一种方法是每天为所有合格用户重新颁发新的证书,使得证书被撤销的用户无法使用旧证书访问资源,此方法中,合法用户进行证书验证和管理员重新颁发证书的通信成本高,与成员数线性相关。上述撤销方案的困难度与合法成员数线性相关。为了解决此类撤销问题,CAMENISCH等[6]提出了基于动态累加器的成员撤销系统。在该方案中,群管理员充当累加器管理员的角色,将合法证书聚合成累加值。当撤销成员时,群管理员用累加器陷门信息更新累加值。由于动态累加器在撤销证书时,更新累加值和证据的计算量与合格成员数和撤销用户数量无关,所以大大提高了成员资格撤销的效率。 近年来,区块链的扩容技术[19,40,46-47]有很多,其中无状态区块链[19]是一项很重要的扩容技术。如在比特币中,当节点A向B发起一笔转账时,除了需要通过签名来验证这笔交易是否是A发起的,还要验证A是否有这笔钱。在传统验证方法中,验证节点维护网络中每个节点的未花费交易集合UTXO[19],验证节点通过查看节点A发起的交易是否在UTXO集合中来判断A是否发起了合法的转账。然而,随着参与比特币交易的用户越来越多,UTXO集合越来越大,验证节点的存储压力也越来越大。除了比特币等基于UTXO模型的区块链面临这样的问题,基于账户的模型,如以太坊也面临着同样的问题。为了解决此类问题,BONEH等[19]提出了基于支持批处理累加器的无状态区块链。在该无状态区块链的构造中,验证节点无需存储整个UTXO集合,只需存储该UTXO集合中元素的累加值,用户节点存储与自己相关的UTXO及证据。当进行一笔交易时,交易发起者会提供附带证据的交易给验证节点,验证节点通过判断交易和证据是否通过验证来确定这笔交易是否合法。此外,批处理累加器可以对交易进行高效批量验证,不仅减轻了全节点的存储压力,而且进一步提高了验证效率。在此之后,也产生了很多区块链扩容技术[19,40,46,47]。 笔者主要围绕密码累加器的相关研究内容展开综述,并按实现方式、功能对累加器进行了分类,详细描述了基于RSA的累加器、基于双线性映射的累加器和基于Merkle哈希树的累加器的经典构造。经过分析,现有的累加器方案仍然存在一些不足,未来的研究方向可以关注以下几点: (1)基于双线性对的累加器解决了累加元素必须为素数的不足,然而,该类累加器的公开参数的大小与集合的大小相同,增加了通信代价。此外,累加器的大小需提前设置,即累加器包含的元素个数固定。在动态应用场景中,元素的个数不断增加,若参数设置过大,则增加公开参数的传输开销;若参数设置过小,则应用场景受限。因此,如何突破双线性映射累加器的大小限制成为未来研究的方向之一。 (2)在可验证外包数据存储中,使用数字签名、布隆过滤器、Merkle哈希树等验证数据结构验证外包数据的完整性,具有证据生成和验证效率高等优点。然而,该类数据验证结构为私有验证,即只有拥有私钥的用户才能验证结构,使得使用场景受限。向量承诺、密码累加器可以实现公开验证,然而,构造和验证效率低下。因此,如何构造高效的密码累加器,应用于动态密文检索、无状态区块链、分布式存储系统是未来研究的方向之一。5 三类密码累加器的分析与比较
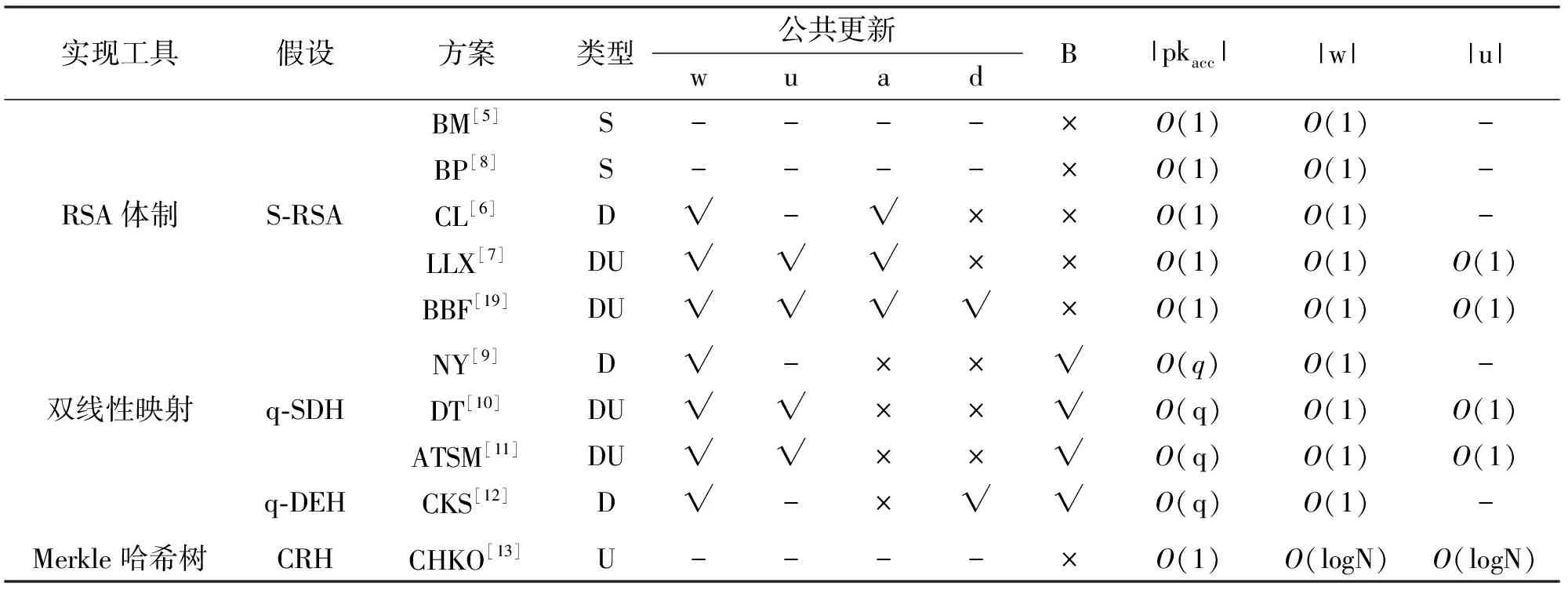
6 应 用
6.1 时间戳
6.2 成员资格撤销
6.3 无状态区块链
7 总结和展望

