针对Fruit v2和Fruit-80的差分错误攻击

乔青蓝，董丽华

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

近年来RFID标签、智能卡和FPGA的影响不断扩大。在这些设备中，内存、电池供电和计算能力有限，因而硬件和软件的效率与安全性至关重要，进而设计资源受限条件下的轻量级密码算法已经成为信息安全领域的重大挑战。在过去的十几年里，许多流密码，例如Grain[1-2]、Trivium[3]、MICKEY 2.0[4]等被相继提出。然而为了抵抗时间记忆数据权衡(TMD)攻击[5-6]，所有这些密码都使用了一个相对较大的内部状态来生成密钥流，并不适用于资源受限的情况。

2015年，ARMKNECHT等[7]学者为减少内部状态同时不损害其对时间记忆数据权衡攻击的安全性，给出了一个全新的设计原则，即密钥不仅参与初始化阶段(KLA)，还参与了密钥生成阶段(PRGA)。基于这一原理，他们提出了第一个小状态流密码Sprout。众多密码学者针对Sprout进行了密码分析[8-13]。虽然分析发现Sprout结构是不安全的，但是近几年基于此原理相继提出了许多超轻量级流密码，例如Plantlet[14-15]，Lizard[16]以及Fruit v2[17]等。其中Fruit v2[17]是2016年，Ghafari为了抵抗针对Sprout的密钥恢复攻击，通过使用更复杂的轮密钥函数对Sprout结构给出的改进版本。目前Fruit族已有4个版本： Fruit-v2[17]、Fruit-80[18]、Fruit-128[19]和Fruit-F[20-21]。但是Fruit族作为Sprout的继承者，内部依然存在着与Sprout类似的弱点。2017年，文献[22]对Fruit进行了快速相关攻击，并指出使用262.8轮Fruit加密和222.3个密钥流可以有效确定其80位密钥。随后他们对Plantlet和Fruit进行区分攻击[23]，并提出Fruit的首个密钥恢复攻击，结果显示Fruit中至少有264个弱密钥。2019年，文献[24]对类Grain小状态流密码发起了快速相关攻击，并指出对于Fruit v2使用255.34加密和255.62个密钥流比特可以有效确定密钥，对于Fruit 80使用262.82的数据和内存复杂度以及264.47的时间复杂度可以有效确定密钥。2019年，文献[25]采用分而治之的方法对Fruit进行攻击，比穷举密钥搜索快16.96倍左右。2020年，文献[20]提出了具有长周期的轻量级轮密钥的小状态流密码Fruit-F以避免快速相关攻击。同年，文献[26]对Fruit-80进行相关攻击，结果显示可以恢复Fruit-80的全部密钥，因此设计者对于密钥流的长度限制是不够的。由此可见，Fruit族密码结构虽然是对Sprout的改进，但其结构依然存在着弱性，需要进一步研究和改进。

另一方面，在密码算法的实现中，通常使用寄存器来存储数据和内部状态，因而使用具有较低代价如电压跳变、时钟刺激、激光等方法，即可向寄存器中注入错误[27-29]，因此差分错误攻击对密码算法具有巨大的威胁。1997年，文献[30]首次提出了差分错误攻击的概念，将这种攻击方法应用于分组密码算法，成功攻击了数据加密标准(Data Encryption Standand，DES)，此后差分错误攻击成功地应用于众多分组密码算法[31-40]。一般来说，差分错误攻击对于流密码算法同样有效。2004年，文献[41]在其发表的论文中试图找到一种差分错误攻击的方法，用来分析所有流密码。2008年，文献[42]对Trivium进行了差分错误攻击，通过注入43个错误成功恢复了Trivium的密钥。同年，文献[43]对该攻击算法做了进一步改进，只需一位错误注入就可以恢复密钥。2009年，文献[44]介绍了一种基于真实故障模型的针对GRAIN-128的故障攻击并给出了对抗措施。2011年，文献[45]证明了Grain-128也可以通过在非线性反馈移位寄存器(Nonlinear Feedback Shift Register，NFSR)中诱发故障而受到攻击，该攻击需要在NFSR中注入56个错误，计算复杂度约为221。2012年，BANIK等学者分别在宽松故障模型下[46]和严格故障模型下[47]对Grain族进行差分错误攻击。2012年，文献[48]对Trivium算法进行了错误攻击，该模型不假定攻击者可以同步故障注入的时间。2013年，文献[49]提出了对MICKEY-128 2.0的差分错误攻击。2015年，文献[50]对Grain的差分错误攻击提出了进一步的改进，进一步减少了错误插入数量 。目前对于流密码的错误攻击的研究成果主要集中在对Trivium，Grain，MICKEY，Rabbit和Sosemnauk等密码。在小状态流密码方面，2015年，文献[8]对Sprout进行了差分错误攻击，攻击中通过使用120个错误恢复了Sprout的密钥。基于此，2017年，文献[15]对Plantlet进行了差分错误攻击，仅需要4个故障就可以在数小时内恢复Plantlet的密钥，随后，文献[51]首次对Lizard进行了差分错误攻击，并且表明只需要5个错误就可以恢复内部状态，但不能恢复完整密钥。目前对轻量级小状态流密码的差分错误攻击研究成果较少，针对Fruit族的差分错误攻击更是尚未展开，因此笔者尝试将差分错误攻击应用于小状态流密码Fruit族的安全性分析。

在相对宽松的错误模型假设下(即攻击者可在密码内部状态的某个随机位置在每次重启执行过程的同一时刻注入单个错误)，通过求解利用输出函数的一阶差分性质得到的内部状态的线性方程组，笔者分析了密码的整个内部状态。研究结果表明，在216.3的时间复杂度下即可恢复Fruit v2和Fruit-80的内部状态。在恢复密钥部分，借助Cryptominisat-2.9.5 SAT解算器[40]对非线性方程组进行求解，只需要大约10 min即可完成所有方程的求解。通过统计显示，攻击所需错误个数为27.3。

1 Fruit流密码的介绍

Fruit系列流密码是超轻量级小状态流密码的最新版本，正是由于它较小的内部状态吸引了全世界密码学界的广泛关注。该系列目前由4个版本的密码组成：Fruit v2、Fruit-80、Fruit-128和Fruit-F。每个版本的密码在密码分析方面都有独特的挑战。本节将深入介绍Fruit族的算法结构。

2016年，GHAFARI等学者在IACR(eprint)的网页上首次非正式地介绍了Fruit v2密码并进行了简单的密码分析[17]。2018年，Fruit-80作为更易于实现和安全的更新版本而出现[18]。

Fruit-v2和Fruit-80在设计中的新想法如下所示：

(1) 新的轮密钥函数(Sprout的大多数弱点与轮密钥函数有关)；

(2) 新的初始化过程，以加强对相关密钥攻击的抵抗能力；

(3) 防止线性反馈移位寄存器(Linear Feedback Shift Register，LFSR)初始化后内部状态全为零的新思路(与Grain家族和Sprout不同)；

(4) 增加线性反馈移位寄存器的大小以在每次加载中获得更长的密钥流；

(5) 新的针对非线性反馈移位寄存器的更轻的反馈函数和输出函数(与Grain-v1和Sprout相比)。

1.1 Fruit族密码结构

通过对比如表1所示的Fruit族的各版本结构，可以发现除了轮密钥及内部更新函数，结构的其他部分大体相同。

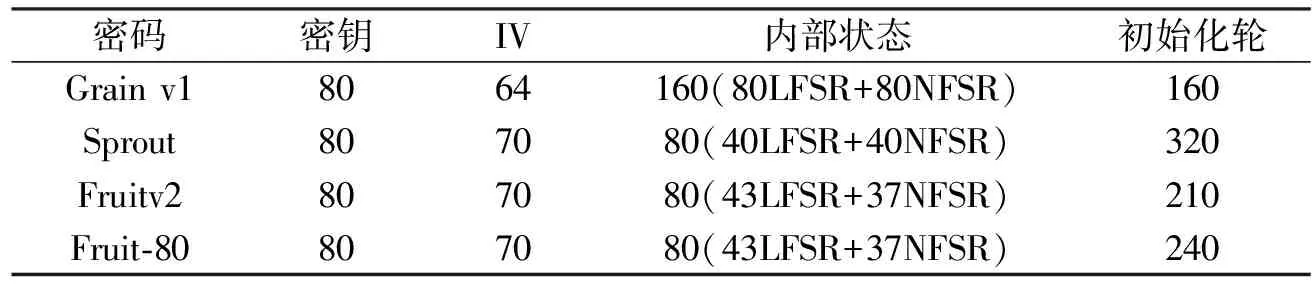
表1 Fruit 族相关密码对比

因此，笔者对各版本的相同结构部分给出了如图1所示Fruit族小状态流密码的广义模型，此模型由以下几部分组成。

图1 Fruit 族小状态流密码的广义模型

LFSR：设m为线性反馈移位寄存器的内部状态的大小，Lt=(lt，…，lt+m-1)为线性反馈移位寄存器在时刻t的内部状态，f为线性反馈移位寄存器的内部状态更新函数，即Lt+1=(lt+1，…，lt+m)，lt+m=f(Lt)，并且其逆过程是Lt-1=(lt-1，…，lt+m-2)，lt-1=f′(Lt)。

NFSR和计数器：设m′为非线性反馈移位寄存器的内部状态的大小，Nt=(nt，…，nt+m′-1)为t时刻非线性反馈移位寄存器的内部状态，非线性反馈移位寄存器按以下方式递归更新：

(1)

1.2 Fruit族密码的完整数学描述

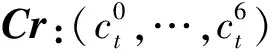
图2 Fruit v2的具体结构 图3 Fruit-80的具体结构

(2)

其中，

(3)

(4)

(5)

其中，

(6)

g函数：非线性反馈移位寄存器的反馈更新函数如下：

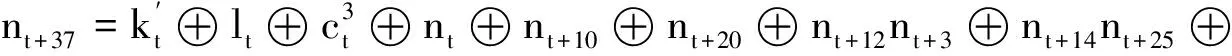
(7)

Fruit-80的非线性反馈移位寄存器的反馈函数与Fruit v2大致相同，不同之处为Fruit-80的g函数少了计数器的参与：

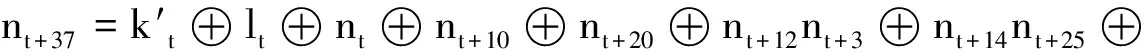
(8)

f函数：Fruit v2和Fruit-80的线性反馈移位寄存器的反馈更新函数为

lt+43=lt⊕lt+8⊕lt+18⊕lt+23⊕lt+28⊕lt+37。

(9)

h函数：此函数从LFSR和NFSR状态中生成预输出流，如下所示：

h(lt+6，lt+15，lt+1，lt+22，nt+35，lt+27，lt+11，lt+33，nt+1，nt+33，lt+42)=
lt+6lt+15⊕lt+1lt+22⊕nt+35lt+27⊕lt+11lt+33⊕nt+1nt+33lt+42。

(10)

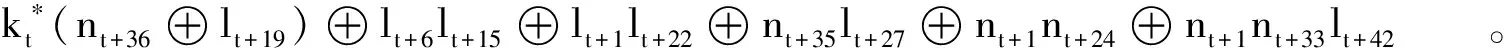
(11)

输出函数：输出密钥流由非线性反馈移位寄存器的7位、线性反馈移位寄存器的1位和h函数的输出产生，如下所示：

(12)

其中，BFruit v2={0，7，13，19，24，29，36}，BFruit-80={0，7，19，29，36}。

密码初始化：在初始化阶段，首先进行密钥加载。将80位的密钥K分别载入线性反馈移位寄存器和非线性反馈移位寄存器，其中K的前37位载入非线性反馈移位寄存器，即n0=k0，n1=k1，…，n36=k36，剩余的43位载入线性反馈移位寄存器，即l0=k37，l1=k38，…，l42=k79，两个计数器均置为0，Fruit v2的IV通过在前面添加1个比特1和9个比特0，在后面添加50个比特0，扩展为130个比特IV′，形如：IV′=1000000000v0v1，…，v6900…00。Fruit-80的IV通过在前面添加1个比特1和9个比特0扩展为80个比特IV′，即，IV′=1000000000v0v1，…，v69。

2 故障位置检测算法

本节借鉴MAITRA等[8]所提出的基于特征向量和错误路径之间的相关性确定位置的方法，给出适用于所有Fruit族的故障位置识别算法，并使用此算法对Fruit v2和Fruit-80进行实际故障位置识别。

在攻击之前，先来介绍一些将要使用的符号：

(1)St=[nt，nt+1，…，nt+m′-1，lt，lt+1，…，lt+m-1]，用于表示t时刻的内部状态。其中nt+i(lt+i)表示t时刻的第i位非线性反馈移位寄存器(线性反馈移位寄存器)。当t=0时，为了方便起见，使用S0=[n0，n1，…，nm′-1，l0，l1，…，lm-1]来表示密钥流产生阶段的初始内部状态。

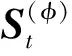
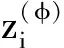
当0≤i≤λ-1，为了形成密钥流序列的惟一模式，给出以下定义[8]。

定义1特征向量Q(φ)，将其定义为

(13)

其中，

(14)

这个概率是通过预先进行足够多的实验来估计的。特征向量Q(φ)可以在攻击的离线阶段被预先计算出来，然后存储起来与差分密钥流进行比较。

定义2假设在未知位置δ(0≤δ≤80)注入了一个错误，定义

(15)

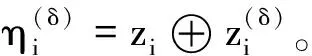
未知位置δ(0≤δ≤80)的错误路径Γ(δ)可以定义为

(16)

注意，在这种情况下没有概率，也就是说，可以通过比较每个Q(φ)和Γ(δ)来估计准确的错误位置。

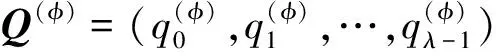
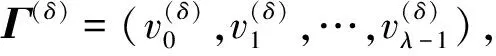
① maxφμ(Q(φ)，Γ(δ))

②μ(Q(δ)，Γ(δ))

③α(Q(δ))=#|{μ(Q(φ)，Γ(δ))>μ(Q(δ)，Γ(δ))}|

图4统计了Fruitv2和Fruit-80的maxφμ(Q(φ)，Γ(δ))和μ(Q(δ)，Γ(δ))指标：

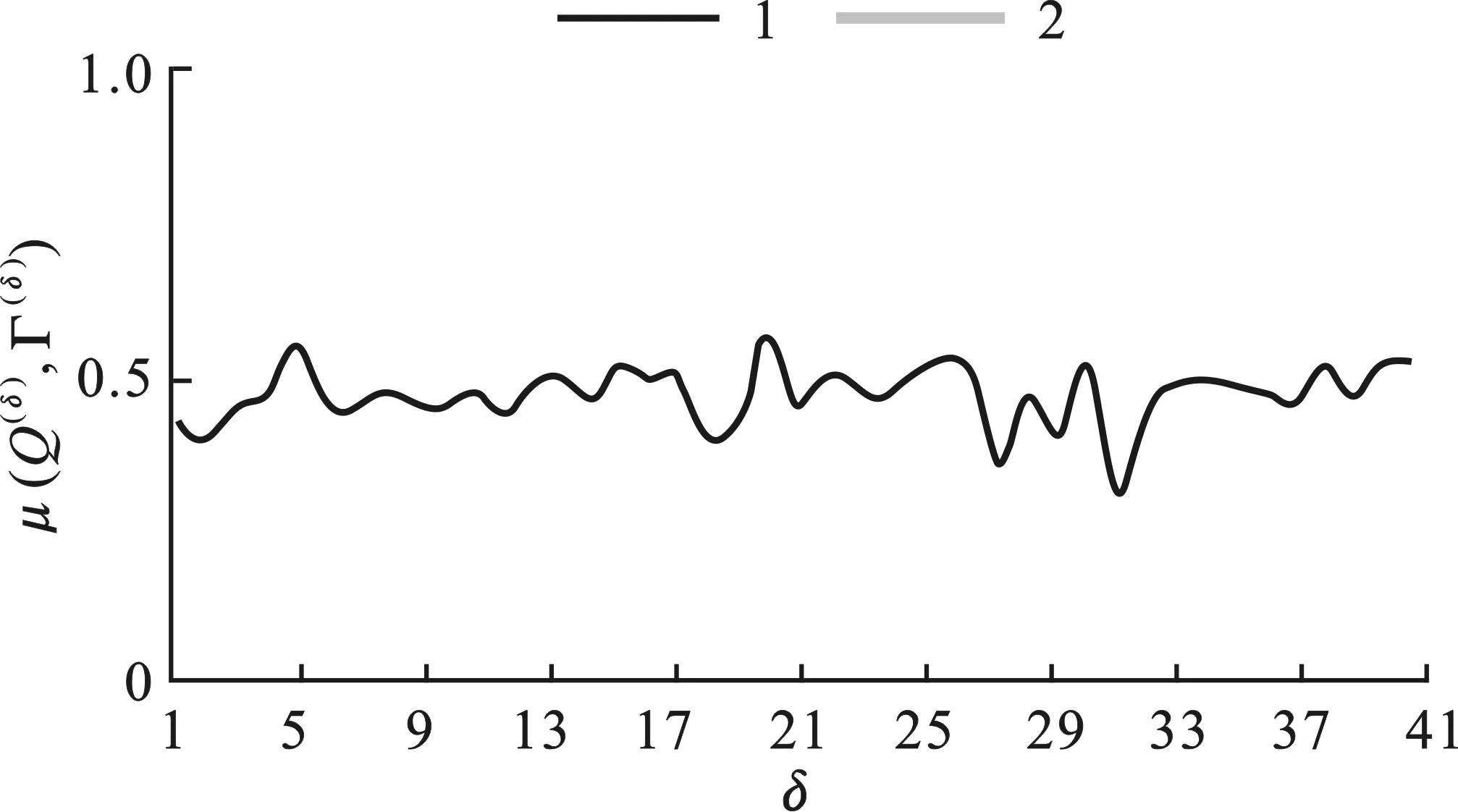
(a) Fruit v2 (b) Fruit-80

在图4中，当μ(Q(δ)，Γ(δ))接近maxφμ(Q(φ)，Γ(δ))，即α(Q(δ))较小时，更容易定位这些错误。然而，如果μ(Q(δ)，Γ(δ))远小于maxφμ(Q(φ)，Γ(δ))，即α(Q(δ))较大，则意味着从差分密钥流中更难定位该特定错误位置。将文献[8]中的图3和文献[15]中的图3与笔者的结果进行对比发现，与Sprout和Plantlet相比，Fruit v2和Fruit-80的α(Q(δ))更小，更易定位错误位置。

下面对错误位置检测方法进行具体描述：假设每个错误都是在每次初始化过程结束后的初始内部状态随机注入的，统计密码在状态φ处注入错误后的特征向量Q(φ)，在具体实现时令λ=64，在攻击之前用随机的密钥初始化向量对将密码算法运行215轮，统计注入错误前后密钥流之间的关系，并计算(Q(0)，Q(1)，…，Q(m+m′))，然后获取在具体位置δ注入错误对应的错误路径Γ(δ)，通过对Γ(δ)和Q(φ)(0≤φ≤m+m′)比较来确定错误位置。确认错误位置的具体步骤为

① 在任意位置注入一个错误δ；

③ 对每个状态位置φ计算μ(Q(φ)，Γ(δ))；

④ 对于每个错误，根据μ(Q(φ)，Γ(δ))建立一个等级表Tδ，以更高的优先级排列可能的错误位置φ。

算法1给出了检测错误位置的一般步骤。

算法1位置识别算法。

输入：签名向量(Q(0)，Q(1)，…，Q(m+m′))以及τ个不同的错误δ1，δ2，…，δτ。

输出：候选等级表Tδ。

Fori=1 toτdo

获取错误路径：

Forφ=0 tom+m′ then

计算μ(Q(φ)，Γ(δi))

计算maxφμ(Q(φ)，Γ(δi))

End

找到maxφμ(Q(φ)，Γ(δi))对应的φ0，令δi=φ0

计算μ(Q(δi)，Γ(δi))

Ifμ(Q(δi)，Γ(δi))=maxφμ(Q(φ)，Γ(δi)) then

Tδ=[φ0]

ElseTδ=[φ0]

计算μ(Q(φ)，Γ(δi))中次小于maxφμ(Q(φ)，Γ(δi))的系数对应φ1

重复第1步

Tδ=[φ0，φ1]

以此类推

End

returnTδ。

算法1的整体复杂度为τ(m+m′)。使用上述识别算法对Fruit v2和Fruit-80进行了实际错误位置识别。实验结果表明，对于Fruit v2在第一次筛选之后全部故障位置都被精确识别出，因此Fruit v2准确识别单个错误的复杂度为一次算法的复杂度O(26.3)。而对于Fruit-80第一次筛选之后只有小部分故障位置没有精确识别出，其中最难识别的故障为l23，对应T23的长度为2，即Fruit-80准确识别单个错误的复杂度为执行两次算法的复杂度O(27.3)。预计算阶段即计算特征向量Q(φ)的时间复杂度为O(226.5)，数据复杂度为O(211.5)。

3 针对Fruit v2和Fruit-80的差分错误攻击

一旦攻击者能够推断出注入错误的位置，就可以继续使用此信息对密码发起攻击。在本节中，将在最宽松的假设下对Fruit家族进行攻击，即假设攻击者有能力执行以下操作：

① 在同一个随机寄存器位置注入多个时间同步的单位翻转错误；

② 重置执行密码的设备并重新启动密码。

在本节中，将以Fruit v2为例来说明新方法，但是，这种攻击同样适用于Fruit系列的任何版本。这种错误攻击主要基于Fruit系列的各版本的输出布尔函数h的特定性质，即h函数满足文献[46]中提出的如下仿射差分函数性质：

定义5对于具有q个变量的布尔函数F，如果F满足对任意一个非零向量α∈{0，1}q，F(x)+F(x+α)是一个仿射函数，则α是F的一个仿射差分。如果布尔函数没有仿射差分，则称其为抗仿射差分函数。

例如，对于Fruit v2的滤波函数h(式10)，满足

h(lt+1)+h(lt+1+1)=(lt+6×lt+15⊕lt+1×lt+22⊕nt+35×lt+27⊕lt+11×lt+33⊕nt+1×nt+33×

lt+42)+(lt+6×lt+15⊕(lt+1+1)×lt+22⊕nt+35×lt+27⊕lt+11×lt+33⊕

nt+1×nt+33×lt+42)=lt+22。

(17)

可见h是仿射差分为α={0，0，1，0，0，0，0，0，0，0，0}的一个仿射函数。

利用这一差分性质，在密钥流产生阶段开始时，可以对线性反馈移位寄存器的状态变量建立若干个线性方程，并通过求解这些方程得到完整的线性反馈移位寄存器状态。而非线性反馈移位寄存器的移位性质将帮助确定非线性反馈移位寄存器的状态位。鉴于这一背景，内部状态恢复过程将包括以下步骤：

① 攻击者在随机选择的线性反馈移位寄存器位置注入一个错误，并通过比较无错误和错误密钥流及上一节中提出的错误位置识别算法来确定错误位置。

② 通过比较特定密钥流产生阶段中的无错误和错误密钥流，根据布尔函数h的仿射差分性质，可以得到PRGA开始时线性反馈移位寄存器状态位的线性方程。运行适当次数的错误攻击，得到几个这样的线性方程组，通过求解线性方程组得到线性反馈移位寄存器状态。

③ 如上所述，将无错误和错误密钥流在某些其它PRGA轮中进行比较，得到在PRGA开始时非线性反馈移位寄存器的某些特定位置的值，根据非线性反馈移位寄存器的移位性质确定非线性反馈移位寄存器的值。

3.1 确定LFSR的内部状态

lt+22=l37⊕l33⊕l29⊕l28⊕l24⊕l23⊕l18⊕l14⊕l6⊕l8⊕l0。

(18)

以此类推，可以获得43个变量为l0，l1，…l42的线性方程，其中27≤t≤68。用矩阵表示为LY=W，矩阵L是线性函数lt+22，其中27≤t≤68，Y=[l0，l1，…，l42]T，W是一个列向量：

(19)

使用Matlab对矩阵L进行逆运算，结果证明矩阵L是可逆的，所以通过注入错误和计算W可以立刻求出向量Y=L-1W。此时可以确定线性反馈移位寄存器的全部状态。主要消耗时间与内存的是Y=L-1W的计算过程，它大概需要43×43位来存储L-1和433≈O(216.3)的时间复杂度。

3.2 确定NFSR的内部状态

在注入错误之前可以使用相同的(K，IV)对密码进行重置，Fruit v2和Fruit-80的密钥流输出函数的表达式为式(12)；由于现在线性反馈移位寄存器的内部状态已知，如果错误位置在n33，那么注入错误后产生的密钥流输出函数分别为

nt+1(nt+33+1)lt+42⊕nt⊕nt+7⊕nt+13⊕nt+19⊕nt+29⊕nt+24⊕nt+36⊕lt+38，

(20)

nt+1nt+24⊕nt+1(nt+33+1)lt+42)⊕nt⊕nt+7⊕nt+19⊕nt+29⊕nt+36⊕lt+38。

(21)

3.3 密钥恢复阶段

在之前的分析中成功地恢复了Fruit系列密码的内部状态S0，然而这并不能直接恢复密钥。因为在轻量级流密码算法中，密钥不仅参与初始化阶段，而且也参与了密钥生成阶段，这使得密钥恢复变得更加困难。

在Fruit v2和Fruit-80中参与非线性反馈移位寄存器更新的轮密钥函数的每个密钥位都是由计数器Cr决定的，在初始化的第1阶段(Fruit v2为130轮，Fruit-80为80轮)，Cr从0开始计数直到结束，在初始化的第2阶段，Cr的7位被重新分配，由非线性反馈移位寄存器的6比特最低有效位和线性反馈移位寄存器的1比特最低有效位组成。因此对于Fruit v2和Fruit-80可以将密钥恢复阶段分为3步进行。

3.3.1 获取连续128位轮密钥比特

密钥恢复过程中的难点主要是内部状态更新过程中有轮密钥函数和计时器的参与，而轮密钥函数和计时器都是未知的，又由于轮密钥函数中参与的密钥是由计时器决定的，因此，首先对计时器Cr进行猜测，Cr由7比特组成，因此Cr有27种可能性。在密钥流产生阶段的初始时期，内部状态S0已知。

nt+35lt+27⊕nt+1nt+42⊕nt+1nt+33lt+42。

(22)

对于Fruit v2，由于轮密钥只参与非线性反馈移位寄存器的更新，因此可以通过输出函数zt来获取非线性反馈移位寄存器的反馈位(即n36)的值，再通过非线性反馈移位寄存器的更新函数获取这一时刻的轮密钥函数k′的值：

nt-7×nt-17⊕nt-4×nt-22×nt-30⊕nt-27×nt-29×nt-31×nt-33。

(23)

3.3.2 根据轮密钥函数建立方程组

对于Fruit v2，可以建立针对k′的方程组。由于对每个计时器的值都可以构成一个轮密钥函数k′，假设在密钥流产生阶段Cr输出为127，此时：

s=31，y+32=63，u+64=79，p=15，q+16=47，r+48=79 。

(24)

因此可以建立方程组：

(25)

为了消除方程组中的二次项，猜测：(k0，k1，k2，…，k31)，通过高斯消去求解128个线性方程组来获取其余的48位密钥，因此获取密钥的复杂度为27×232×1283=260。

(26)

为降低计算的难度，笔者猜测(k0，k1，k2，…，k15，…，k48)，将非线性函数组转换为线性函数方程组，然后使用高斯消去求解128个线性方程组获取剩余的32位密钥，此时获取密钥的复杂度为27×248×1283=277；复杂度相对较高，也可以直接使用SAT解算器求解128个非线性方程来获取80位密钥，因此获取密钥的复杂度由SAT解算器确定。借鉴文献[52]中表5使用SAT解算器对Grain差分错误攻击所建立的方程进行求解的结果，估算出求解128个非线性方程所需的时间最多为3.2 s。因此求解27个这样的方程组所需时间大概为409.6 s。

3.3.3 检测密钥的正确性

通过上述方法，可以得到27组候选密钥，在这一阶段要从候选的密钥中选择一个正确的密钥。逆运算密码80轮，判断计时器Cr的7位是否符合前6位来自非线性反馈移位寄存器的最低有效位，第7位为1。

上述方法对Fruit v 2和Fruit-80均适用，因为这两个密码算法的轮密钥函数中密钥的参与位置由计数器Cr决定，且3个轮密钥函数的周期都是有限且在密钥流限制范围内的，因此可以建立有限个方程并确保所有密钥位均参与运算，通过求解方程组获取密钥。

3.4 复杂度分析

错误个数直接取决于要执行的重置密钥IV的数量，以便覆盖线性反馈移位寄存器中几乎所有位置，由于每次重置密钥和IV后正好有一个错误注入，因此错误注入的预期数目为mlnm(对于m=43，这大约等于27.3)。此后，该攻击需要在一个m×m矩阵和一个m×1向量之间进行一次矩阵乘法来恢复LFSR，并通过求解几个方程来获得非线性反馈移位寄存器状态。由于恢复内部状态建立的方程均为线性方程，因此可以通过高斯消去法求解方程组，因此恢复线性反馈移位寄存器的时间复杂度为O(m3)，恢复非线性反馈移位寄存器的时间复杂度为O((m′)3)。最后，该攻击需要建立轮密钥函数的非线性方程组来恢复密钥，求解非线性方程组部分给出两个方案：一是猜测部分密钥线性化方程，将问题简化为用高斯消去法求解线性方程组，这使得攻击的复杂度很大，为了简化计算难度、降低攻击复杂度；在方案二中，使用SAT解算器求解所有的非线性方程组，统计求解的时间。具体的攻击复杂度对比如表2至表4。

表2 针对Fruit v2和Fruit-80的DFA复杂度对比

表3 SAT解算器恢复密钥时间对比 s

表4 Fruit v2和Fruit-80复杂度对比

4 结束语

借鉴MAITRA等对Sprout的差分错误攻击和BANIK等对Grain的分析，在精确识别错误的基础上，笔者研究了在相对宽松的错误模型下，针对Fruit v2和Fruit-80的差分错误攻击(DFA)。笔者所提出的攻击对Fruit v2和Fruit-80进行差分错误分析。研究结果表明，精确识别单个错误所需的预计算阶段的时间复杂度为O(226.5)，数据复杂度为O(211.5)。以概率1识别Fruit v2单个错误的复杂度为O(26.3)，识别Fruit-80的复杂度为O(27.3)。Fruit v2和Fruit-80恢复内部状态的复杂度为O(216.3)(线性反馈移位寄存器)和O(26.2)(非线性反馈移位寄存器)。而在恢复密钥部分，如果使用猜测部分密钥简化方程的方式恢复密钥，Fruit v2恢复全部密钥的复杂度为O(260)，而Fruit-80恢复全部密钥的复杂度为O(277)，因此与Fruit v2相比，Fruit-80具有更强的抗差分错误攻击的能力。但是如果使用SAT解算器求解非线性方程组来恢复密钥，只需要大约10 min即可完成所有方程的求解，对Fruit-80具有很大的威胁，需要引起更多的关注。