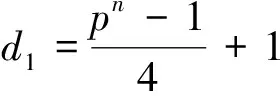有限域上一类完全置换单项式的构造

黄萌濛，伍高飞

(西安电子科技大学 网络与信息安全学院，陕西 西安 710071)

设有限域Fq有q=pn个元素，其中，p是素数，n是正整数。若f(x)为FqFq上的一一映射，则称多项式f(x)∈Fq[x]为域Fq上的置换多项式(Permutation Polynomials，PPs)。有限域上的置换多项式在编码理论以及代数组合论中有着非常重要的应用。在编码理论中，置换多项式可以用来构造最优线性码[1-2]。在代数组合论中，置换多项式可以用来构造具有良好性质的差集系统[3]。完全置换多项式(Complete Permutation Polynomials，CPPs)是一类特殊的置换多项式，除了上述在编码理论和代数组合论中有应用外，完全置换多项式还可用来构造正交拉丁方阵[4-6]，并和最大长度序列(maximum length sequence，m-序列)及其采样之间的互相关值猜想具有密切联系[7]。近年来，研究者又发现利用完全置换多项式可以构造一类在两种不同的广义离散傅里叶变换下具有均匀频谱的布尔函数——Bent-Negabent函数[8]。因此，完全置换多项式的研究无论是在理论上还是应用上都十分有必要。

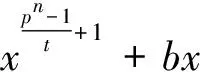
1 预备知识

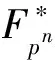
(1)f是双射的；

引理2设f(x)是Fq上的完全置换多项式[9]，则

(1)f(x+a)+b是Fq上的完全置换多项式，其中a，b∈Fq；

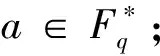
(3)f-1(x)是Fq上的完全置换多项式。

引理2说明，若d是Fpn上的完全置换单项式指数，则d-1(modpn-1)也是Fpn上的完全置换单项式指数。

由AGW准则可以证明：

引理3设p为素数，r，n和d为正整数且满足d|(pn-1)。令h(x)∈Fpn[x]，则f(x)=xrh(x(pn-1)/d)是有限域Fpn上的置换当且仅当下列条件同时成立[18]：

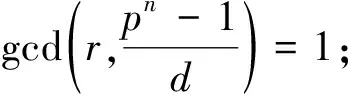
(2)xrh(x)(pn-1)/d是μd上的置换，其中μd是Fpn中阶为d的元素的集合，即

μd={x|xd=1，x∈Fpn} 。

2 完全置换单项式的构造

首先，总结有限域上完全置换单项式指数的已有研究结果；其次，发现并证明一类新的完全置换单项式指数。

利用Magma对完全置换单项式指数展开搜索，总结了完全置换单项式的已有构造，见表1和表2。表1中给出了F2n上完全置换单项式指数的研究结果，表2列出了奇特征有限域Fpn上完全置换单项式指数的研究结果，其中粗体表示的是未被证明的完全置换多项式指数。

表1 F2n上的完全置换单项式指数(2≤n≤12)

表2 Fpn上的完全置换单项式指数

续表2

笔者对近十多年来有限域Fpn完全置换单项式的相关理论研究进行了总结。表3列出了有限域Fpn上完全置换单项式的研究结果。

表3 Fpn上已知的完全置换单项式v-1xd

续表3

续表3

通过观察分析表1和表2中尚未被证明的完全置换多项式指数，发现并证明了一类新的完全置换单项式指数。

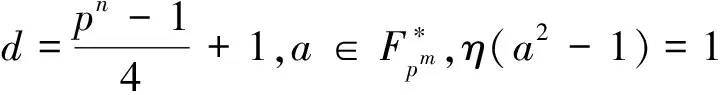
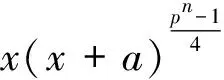
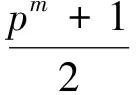
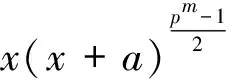
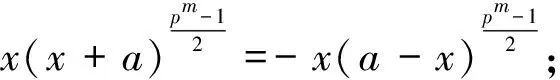
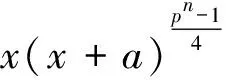
因此，对任意x∈μ4，η(a2-x2)=1等价于η(a2-1)=1且η(a2+1)=1。证毕。

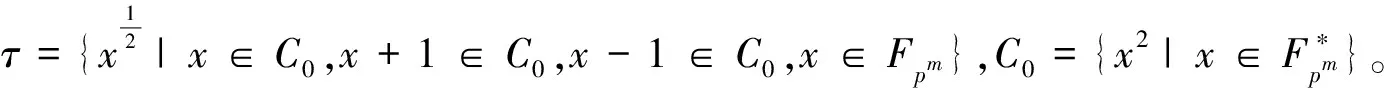
故满足条件的a的个数为

程序结果表明：当p=3，3≤m≤12；p=5，2≤m≤10；p=7，2≤m≤8；p=11，2≤m≤8时，|τ|>0。

后续将考虑集合{x|x∈C0，x+1∈C0，x-1∈C0，x∈Fpm}中元素的个数。

证明 ① 若p≡±3(mod 8)且m是奇数，则p2m≡9(mod 16)。事实上，要证p2m≡9(mod 16)，若令p=8k±3，k为正整数，则只需证p2m≡(8k±3)2m≡9(mod 16)即可。而

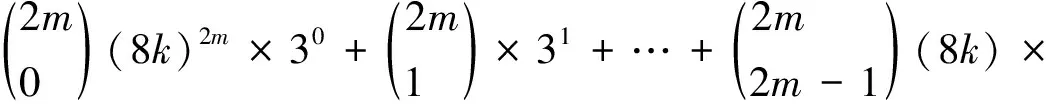
注意到m是奇数，可令m=2l+1，l为正整数，则32m≡9m≡92l+1≡9(mod 16)。

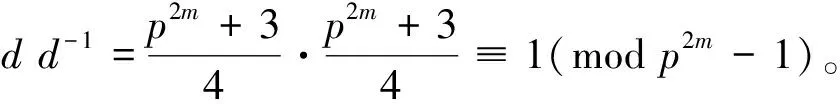
② 若p≡±1(mod 8)或m是偶数，则p2m≡1(mod 16)。证明过程与①中类似，不再赘述。

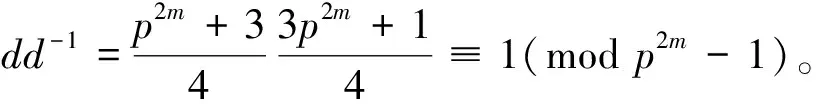
证毕。

综合定理1和命题1，有如下定理：

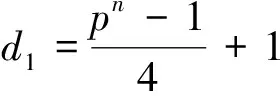
证明d1是Fp2m上的完全置换单项式指数，只需证下面(1)和(2)同时成立即可：

(1) gcd(d1，p2m-1)=1；

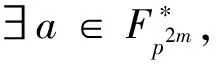
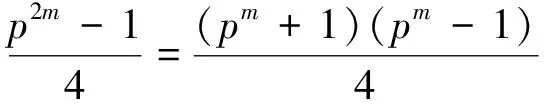
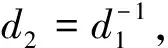
注2利用定理2，可以证明表2中p=7，n=4时，d(d-1)=601(1 801)；p=11，n=4时，d(d-1)=3 661(10 981)为完全置换单项式指数。程序结果表明，当p=3，n=6；p=3，n=10；p=7，n=6；p=11，n=6时，定理1的结论依然成立。故猜测当pm≡-1(mod 4)时，定理1仍成立。

3 结束语

由于完全置换多项式在密码学中的重要应用，构造新的完全置换多项式非常重要。但现有的构造以及计算机搜索验证表明，目前仍有很多完全置换多项式尤其是完全置换单项式指数尚未被刻画。