局部特征值解的无条件稳定FDTD高效实施方案

赵斯晗，魏 兵，2，何欣波，2

(1.西安电子科技大学 物理与光电工程学院，陕西 西安 710071；2.西安电子科技大学 信息感知技术协同创新中心，陕西 西安 710071)

传统时域有限差分方法(Finite Difference Time Domain，FDTD)由于其简单、高效等特点在计算电磁学中占据重要地位，然而传统有限差分方法需满足CFL条件以保证解的稳定性[1-3]。当分析含有精细结构目标的电磁问题时，需要用更小的网格对其进行精确描述，这使得时间步长随之变小，完成一次计算需要大量的时间步数，导致计算效率较低[4]。

为了解决这一问题，JIAO D团队提出了基于滤除空间不稳定模的显式无条件稳定时域有限差分方法(explicit and Unconditionally Stable Finite Difference Time Domain，US-FDTD)[5-6]。由于数值系统的不稳定性是由较大特征值对应的特征模引起的[7]，而这些不稳定模式对所关心频段内的场值贡献很小，因此将其消除不会影响计算结果的精确性。然而，当未知量个数或不稳定模式很多时，求解全域矩阵特征值问题及场值迭代的计算成本仍然很高。

由于系统中的不稳定模式是由空间中的细网格和与细网格紧邻的粗网格造成的[8]，因此笔者给出了一种基于局部特征值求解的显式无条件稳定时域有限差分方法(Unconditionally Stable Finite Difference Time Domain based on Local eigenvalue solution，USL-FDTD)的高效方案用以解决上述计算成本高的问题。笔者将计算域分为两部分，细网格和与之紧密相邻的粗网格为区域I，其余粗网格为区域Ⅱ。于是原始系统矩阵相应地被分为四个局域矩阵块，仅需找到区域I所对应局域矩阵中的不稳定模式即可获得全域不稳定模式。这大大降低了特征值求解及矩阵向量相乘的计算复杂度，降低了内存需求和计算时间。

1 US-FDTD算法基础

为了便于分析，此处考虑无耗问题。麦克斯韦微分方程组差分离散后可写为如下形式[9]：

(1)

(2)

其中，{h}表示计算区域中磁场未知量构成的向量；{e}表示计算区域内电场未知量构成的向量；{j}为激励源矢量；Δt表示时间步长；n，n+1，n±1/2表示时刻；Se表示对电场的旋度算符；Sh表示对磁场的旋度算符；ε表示介电常数；μ表示磁导率；D1/ε表示元素为1/ε的对角矩阵；D1/μ表示元素为1/μ的对角矩阵[9]。

将式(1)代入式(2)，可得

(3)

将式(2)中，n+1→n，n→n-1，n+1/2→n-1/2，得

(4)

联立式(3)和式(4)，可得到电场{e}关于时间的二阶方程：

(5)

其中，{f}n=-(jn+1/2-jn-1/2)/Δt，为-∂j/∂t在n时刻的中心差分[9]。

式(5)实际上为式(6)的中心差分离散：

(6)

系统中的不稳定模式可通过求解全域矩阵S的特征值问题获得：

SΦi=λiΦi，i=1，2，3，…，n，

(7)

其中，λi和Φi分别表示S中第i个特征值和特征向量，n代表S矩阵的维度。若时间步Δt按照采样定理确定，则大于4/Δt2的特征值所对应的特征向量Φi称为不稳定模式[11]。

设Φh为所有不稳定模式构成的矩阵，则式(6)修改为

(8)

对式(8)采用中心差分离散后可得US-FDTD方法的迭代公式[9]：

(9)

2 USL-FDTD方案

2.1 USL-FDTD理论

在计算含有精细结构目标的电磁问题时，由于实际物理尺寸的限制，其空间离散尺度远远小于计算上限频率准确计算所需的空间离散尺度[12]。为满足CFL条件，用于仿真计算的时间步长就会很小。若时间步长不满足稳定性条件，则会导致计算的不稳定。

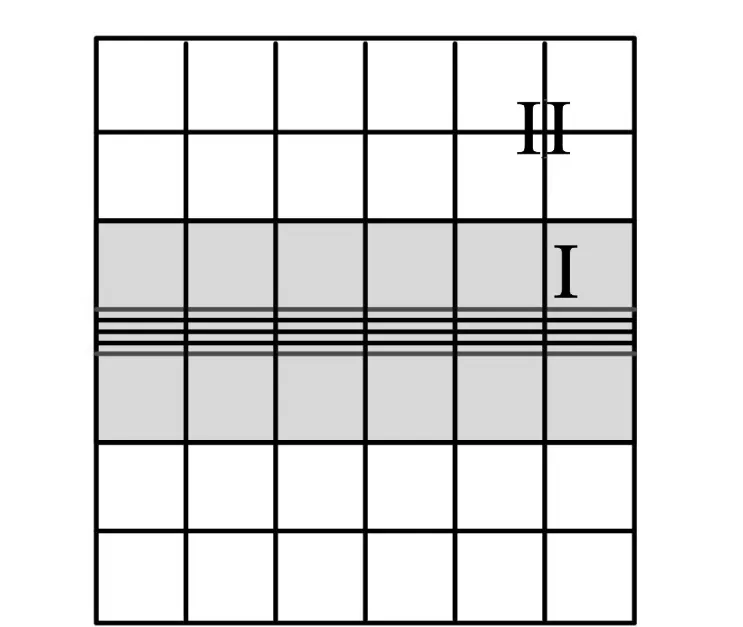
图1 分区域编号示意图

不稳定模式是由空间中的细网格和与细网格紧邻的粗网格造成的[8]，若对计算域未知量进行分组编号，如图1，子域I包含所有细网格和与细网格直接相邻的粗网格对应的未知量；子域Ⅱ包含剩余粗网格对应的未知量。

分别对区域Ⅰ、Ⅱ进行编号。Ⅰ区域粗细网格交界处棱边的电场，如图2所示，需做插值处理。图2中h1和h2分别代表1号和2号面片的磁场，e1～e7代表棱边的电场。“×”代表h2关于e2对称的位置，h×代表未知磁场。l1和l2分别代表h1和h2到“×”处的距离。

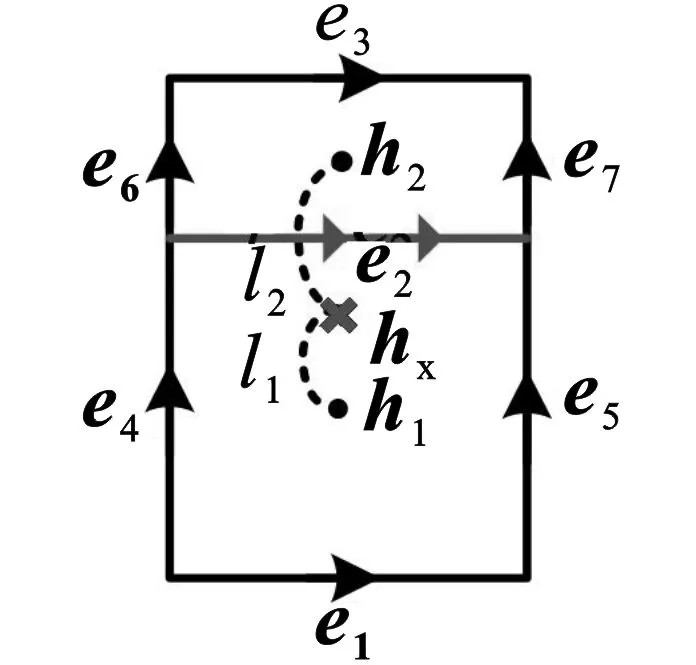
图2 粗细网格交界处示意图

h×可用已知磁场表示为

(10)

e2可表示为

(11)

其中，

(12)

将式(12)代入式(11)中，得

(13)

对边界处棱边所对应的Sh矩阵元素按照式(13)进行更新。

由于Sh经过了插值处理，这时S矩阵不再是一个对称矩阵，需要对不稳定模式Φh进行正交化处理，以满足条件[13]：

(14)

这时S矩阵可自然地被分为4个小矩阵块，分块后的S矩阵和电场未知量{e}向量相乘如图3所示。

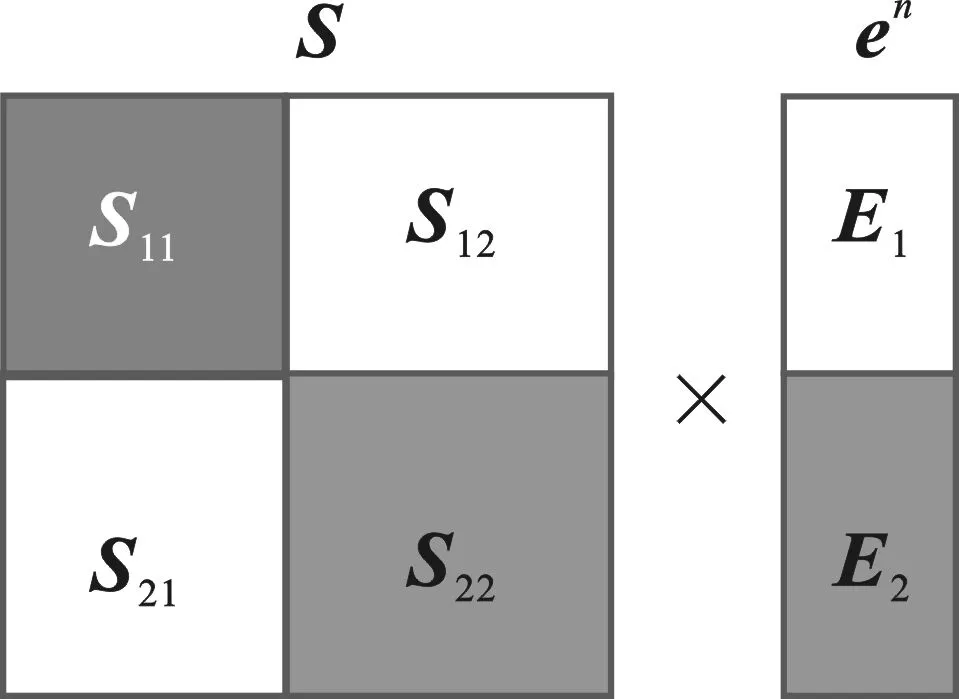
图3 系统矩阵S和电场矢量相乘

图3中，S11矩阵对应子域Ⅰ，包含所有不稳定模式；S22矩阵对应子域Ⅱ，无不稳定模式；S12矩阵和S21矩阵为耦合矩阵，分别代表区域Ⅰ对区域Ⅱ的场值贡献和区域Ⅱ对区域Ⅰ的场值贡献，无不稳定模式。

设{e1}、{e2}分别代表区域Ⅰ和区域Ⅱ的电场未知量，{f}代表激励源项。分组后的S矩阵、未知量{e}和激励源项可写成如下形式：

(15)

式(15)中，只有S11矩阵与细网格及相邻粗网格相关，即不稳定模式仅存在于S11矩阵中。求解S11的特征值问题即可求得全域不稳定模式：

S11Vi=λiVi，i=1，2，3，…，l，

(16)

其中，λi和Vi分别表示S11中第i个特征值和特征向量，l代表S11矩阵的维度。

设Vh代表所有特征值大于4/Δt2对应的特征向量构成的矩阵。由式(6)，通过对S11矩阵的修改，即可消除整个系统的不稳定模式：

(17)

对式(17)采用中心差分离散，可得

(18)

{e2}n+1=2{e2}n-{e2}n-1-Δt2S22{e2}n-Δt2S21{e1}n-D1/ε{f2}n。

(19)

在每个时间步后，需要对{e1}n+1删除额外的零空间模式以保证正确性[14]：

(20)

2.2 复杂度分析

下面从特征值求解及场值迭代两方面分析US-FDTD和USL-FDTD的计算复杂度。

文献[13]和[15]中，US-FDTD方法计算全域矩阵特征值问题的复杂度为O(k2N)，k为不稳定模个数，N为全域矩阵S的维度；而USL-FDTD中，局部特征值问题的复杂度可降低为O(k2n)，n为矩阵S11的维度(n≪N)。因此USL-FDTD提高了特征值求解的计算效率，节省了计算时间。

在式(9)中，全域矩阵和全域电场未知量相乘的复杂度为kO(N)；而在式(18)中，S11矩阵和局域电场未知量相乘的复杂度为kO(n)。因此USL-FDTD降低了矩阵矢量相乘的复杂度，节省了迭代计算的时间。

3 数值结果

3.1 有挡板的PEC谐振腔

在4.00 m×4.64 m谐振腔上下两侧分别加宽度为0.40 m的PEC挡板，构成一个有窄缝的PEC谐振腔，窄缝宽度为0.04 m。由于窄缝很小，因此必须采用细网格模拟。粗网格尺寸为0.10 m，细网格尺寸为0.01 m，网格离散如图4所示，共离散为4 090条棱边。区域I为图中虚线框表示的部分。区域Ⅱ为其余粗网格区域。其中区域I共有526个未知量，区域Ⅱ有3 564个未知量。在(2.00 m，2.32 m)处加微分高斯脉冲线电流源，脉冲宽度为τ=6.666 7×10-9s，t0=5.333 3×10-9s。本例中用传统FDTD、US-FDTD及USL-FDTD分别计算了(3.5 m，0.5 m)处y方向的电场值，结果如图5所示。表1给出了USL-FDTD与传统FDTD和US-FDTD方法的性能对比，使用电脑配置为Intel Core 64×4核处理器，运行频率3.2 GHz，内存8.0 GB。

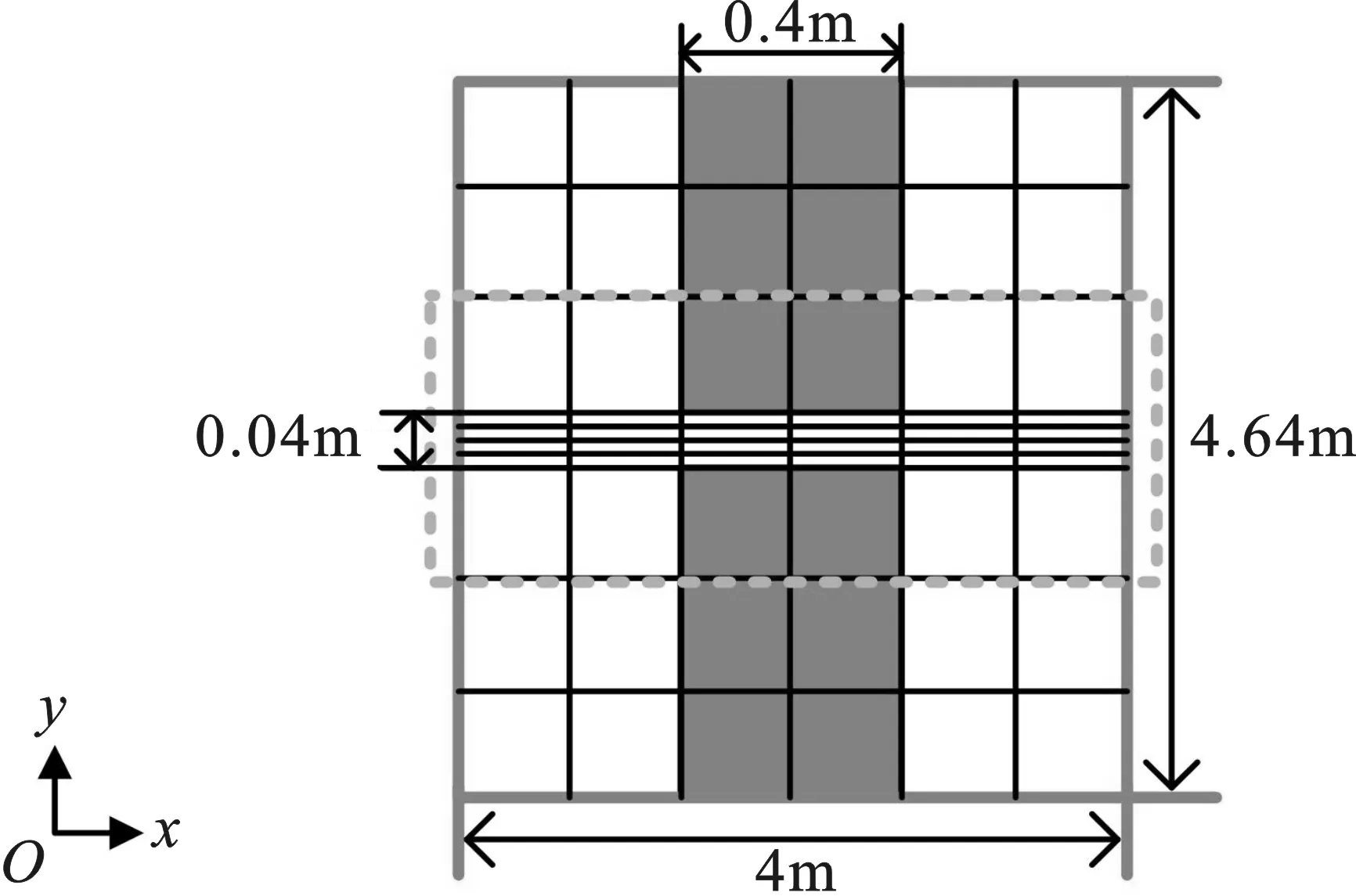
图4 带有挡板的PEC谐振腔

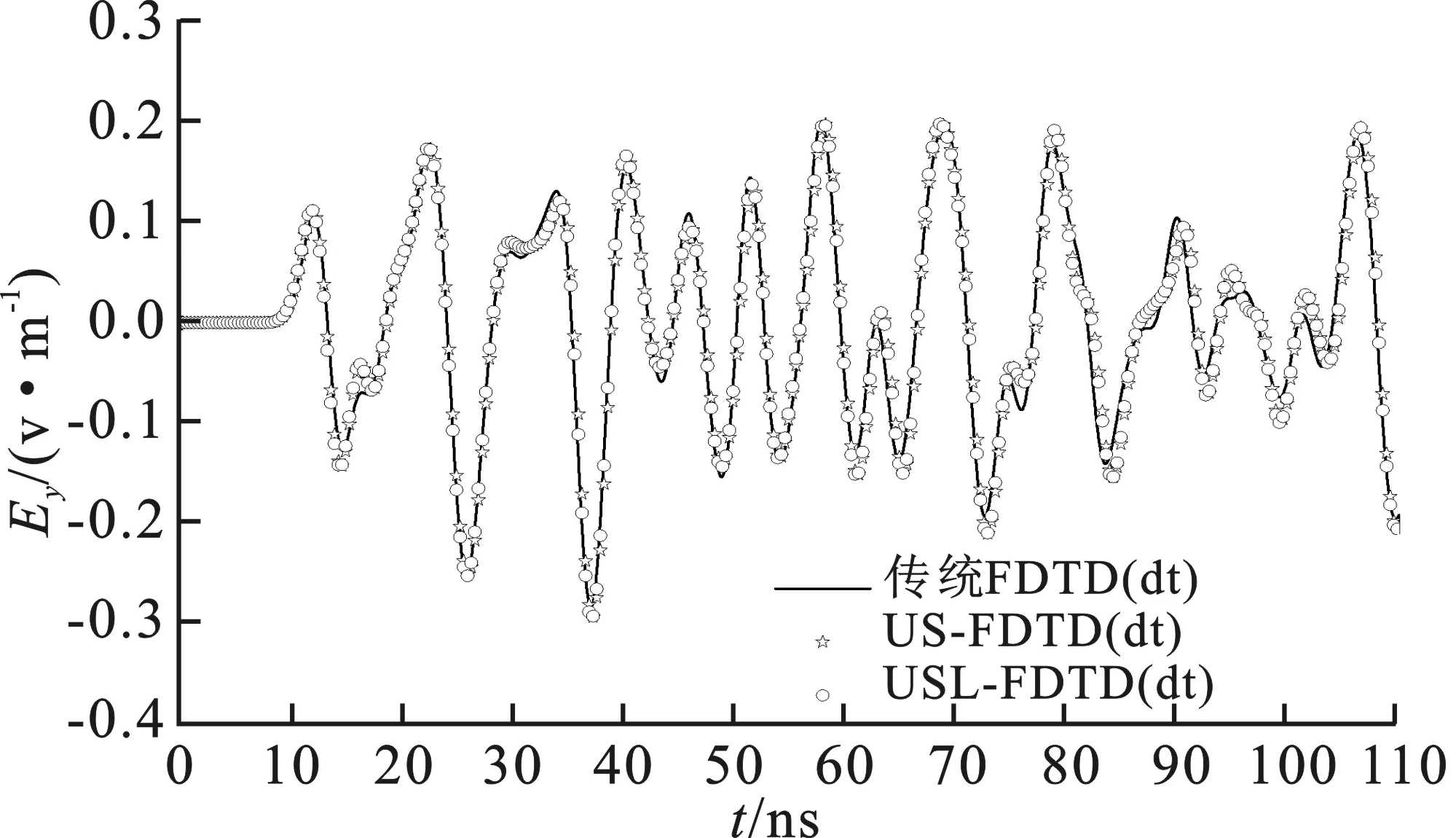
图5 场值计算结果

由图5可看出3个计算结果吻合得很好。表1中，US-FDTD和USL-FDTD方法的时间步长是传统FDTD方法的10倍，因此US-FDTD和USL-FDTD的迭代时间相比传统FDTD方法显著减少。US-FDTD和USL-FDTD需求解矩阵特征值，因此所耗内存比传统方法大；而USL-FDTD仅需求解局域矩阵特征值，矩阵维度大大降低，所以使用的内存比US-FDTD少，且特征值的求解时间大幅减小，计算性能相比前两种数值方法优势明显。

表1 性能对比

3.2 介质板的透射系数

介质板相对介电常数为15，厚度为0.6 cm，如图6所示。

图6 介质板计算模型

粗网格尺寸为1 cm。由于介质板厚度小于一个粗网格的尺寸，为精确模拟，竖直方向需用细网格进行剖分，细网格尺寸为0.1 cm。将计算域离散成640条棱边，其中区域I共有220条棱边，区域Ⅱ共有420条棱边。在介质板上方加一排水平方向的微分高斯脉冲线电流源，脉冲宽度τ=10-9s，t0=8×10-10s。四周采用Mur一阶吸收边界。分别监测无介质板时Q点波形E0和有介质板时Q点透射波形Et，将二者分别做傅里叶变换后的比值作为透射系数。并将USL-FDTD的计算结果与解析法、传统FDTD方法以及US-FDTD方法进行对比，结果如图7所示。

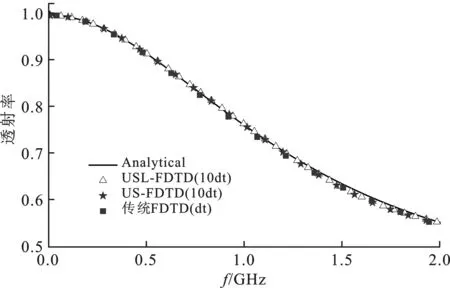
图7 透射系数

由图7可看出4种方法的计算结果一致。在配置为Intel Core 64×4核处理器，运行频率3.2 GHz，内存8.0 GB的硬件条件下，USL-FDTD的时间步长为1.67×10-11s，矩阵维度为220，特征值求解花费0.02 s，迭代花费0.055 s；US-FDTD采用的时间步长为1.67×10-11s，矩阵维度为640，特征值求解花费0.46 s，迭代花费0.069 s。传统FDTD方法的时间步长为1.67×10-12s，迭代耗时11.16 s。以上表明所给方案在处理含精细结构目标的电磁问题时，不仅保证了计算精度，且其计算性能优于传统FDTD和US-FDTD。

4 结束语

笔者给出了一种基于局部特征值求解的显式无条件稳定时域有限差分方法的高效实现方案。该方案和US-FDTD均采用大时间步进行迭代，但并不需要求解全域矩阵的特征值，因此相比US-FDTD方法大大降低了矩阵维度，提高了特征值问题的求解效率，降低了内存需求。通过对谐振腔的场值及介质板透射率的计算，说明在处理含有精细结构目标的电磁问题时，该方案的优势比传统FDTD和US-FDTD方法更为突出。