一种用于高速高精度锁相环的Sigma-Delta调制器设计

马瑞山，刘 芳

（中国电子科技集团公司第五十八研究所，江苏 无锡 214035）

0 引 言

Sigma-Delta调制技术最初的运用是在模数转换领域。引入该技术，是为了降低信噪比对过采样率的依赖性。由于它具有良好的噪声整形功能，使得其应用越来越广泛，在小数分频器中的应用就是一个典型的例子[1-4]。在分频器应用中，Sigma-Delta调制器的输出是不断变化的，调制器连接到多模分频器上使分频比也不断改变。由于调制器的高通特性，最终使得相位噪声往高频处集中，实现噪声整形的目的。锁相环（Phase Locked Loop，PLL）中有一个低通环路滤波器，具有低通特性，可以把集中在高频处的噪声阻隔下来[1]。由于其电路简单而作用却非常明显，所以Sigma-Delta调制技术得到了很多关注和研究，并取得了广泛的应用。

为了适应目前高速高精度数字小数分频锁相环的市场需求，众多学者对Sigma-Delta调制技术进行了研究。文献[2]对用于小数分频的脉冲吞咽分频器进行了结构改造，在脉冲吞咽分频器中加入了脉冲产生器，解决了脉冲吞咽分频器在工作过程中出现误分频以及分频偏移的问题。文献[3]在传统MASH调制器结构中加入反馈抖动电路，避免了传统结构中抖动生成电路的复杂性，同时也减小了电路面积。文献[4]在传统MASH调制器的第一级引入了初始加载值，可以通过调节加载值到达改变PLL最终输出相位的目的，避免了通过加入数字延时调节锁相环输出相位的复杂操作。文献[5]通过脉冲吞咽分频器和加抖动的MASH调制器，实现了高速锁相环的小数分频器设计。以上文献在实现小数分频器时，对Sigma-Delta调制器的时钟频率要求都不高，分频精度最大为24位，所以在对应工艺下都很容易做到。

本设计在文献[4]和文献[5]的基础上，对Sigma-Delta调制器中的累加器进行了优化与改进，设计了并行累加器Sigma-Delta调制器，使Sigma-Delta调制器的速度得到了大幅提升。

1 系统结构及原理

1.1 系统结构

Sigma-Delta小数分频锁相环的系统结构如图1所示，主要由鉴频/鉴相器、电荷泵、低通滤波器、压控振荡器、多模分频器、Sigma-Delta调制器以及SPI寄存器配置模块组成[6-8]。通过SPI总线配置Delta- Sigma调制器的整数值INT、分子值NUM、分母值DEN以及相位微调值SEED，由Sigma-Delta调制器产生不断变化的分频值Frac，多模分频器根据输入分频值Frac实现任意分频比的分频操作，鉴频/鉴相器识别参考频率Fref与多模分频器输出频率之间的误差，并通过电荷泵与低通滤波器将相位误差转换为电压信号控制压控振荡器调节输出频率[9]，最终达到跟踪参考频率Fref的目的。

图1 Sigma-Delta小数分频锁相环系统结构图

1.2 小数分频原理

小数分频是指统计意义上的小数分频，是通过Sigma-Delta调制器不断地按一定规律控制锁相环进行不同的整数分频，最终实现统计意义上的小数分频[9-10]。设多模分频器进行N分频和N+1分频，Tn表示N分频的时间，Tn+1表示N+1分频的时间，则最终的输出频率Fout可表示为

式中：Fout为锁相环输出频率，Fref为锁相环参考频率，N为分频比整数部分，.F为分频比小数部分。

通过SEED值进行相位微调的公式可以表示为

式中：P为锁相环输出的相位移，232为SEED的最大值。相位微调精度为1/232×360°。

1.3 Sigma-Delta调制器噪声整形原理

之所以在小数分频锁相环中采用Sigma-Delta调制器，是因为它具有出色的噪声整形功能，即通过Sigma-Delta调制器可以使相位噪声往高频处集中[11-14]。再加上锁相环的低通特性，可以很容易地把集中在高频处的噪声阻隔下来[15-16]，从而达到降低分频器对整个锁相环环路噪声的影响。下面介绍噪声整形的原理。

如图2（a）所示，在信号量化的过程中，不可避免地会产生量化误差。量化误差的范围为-d/2～d/2。

图2 信号的量化及噪声功率

根据噪声总功率的表示方法，量化噪声的总功率可以表示为

式中：d是量化单位，x代表量化误差。

过采样率OSR定义为

式中：fs为过采样频率，fb为信号频率。

如图2（b）所示，PQ1(f)为过采样前的噪声功率谱，PQ2(f)为过采样后的噪声功率谱。总的量化噪声功率不变，由式（3）和式（4）可以得到：

所以分布在频带内的噪声功率为

由式（6）可知，过采样率越高，频带中的噪声功率PN越小，所以调整过采样率可以进行噪声整形。

Sigma-Delta噪声整形是通过运用累加器和比较结构把噪声推到高频[17-18]，再通过锁相环的低通特性将高频噪声滤除。Sigma-Delta的噪声传递函数可以写为

式中：n是调制阶数。把式（7）代入式（6），可以得到经过整形的被采样信号的频带内噪声为

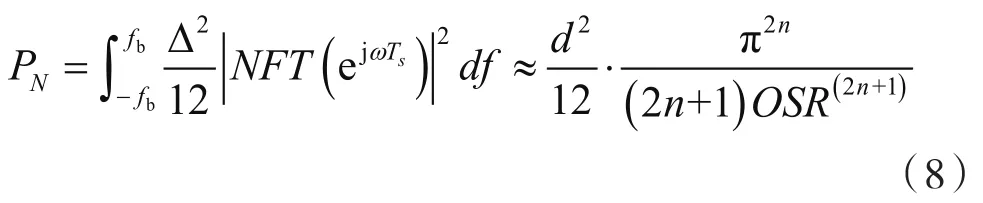
由式（8）可以看出，带内噪声和过采样率及调制阶数有关，调制阶数越大，噪声整形效果越好。

1.4 MASH结构的Sigma-Delta调制器

MASH结构的Sigma-Delta调制器是基于累加器设计的[10]。如图3（a）所示的4阶MASH累加器结构，每个累加器根据输入产生误差值和量化值，最后通过ΔN公式消除误差。

如图3（b）所示，每级累加器的工作过程相同，不同的是第一级累加器多了一个相位微调控制数据SEED。通过调节SEED值可以对锁相环输出相位进行微调。当SEED值为0，其功能与其他累加器完全一致。以第一级累加器为例，累加器的工作过程为：输入累加器的分母为DEN，分子为NUM。每经过一个时钟周期，累加器的值增大NUM，当累加的值超过DEN，则产生一个进位输出信号C。同时累加的结果与DEN比较，当累加的结果没有大于DEN时，累加器延时一个单位时间后输出本次累加的结果，并将此结果反馈回本级累加器进行累加。当累加的结果大于DEN时，累加器延时一个单位时间后输出本次累加的结果减去DEN的值，并将此结果反馈回本级累加器进行累加。

图3 MASH1-1-1-1结构图

为了简化公式推导，这里将输入信号设为X[z]，通过对累加器结构的分析，可以很容易得出一阶累加器的传输函数为

e1[z]为累加器输出的误差信号，最后的移位操作是为了构造高通函数时能消去低阶噪声而设计的。进位输出C1位宽为1，等于经过噪声整形后的量化误差与输入信号之和。其他累加器的传输函数也可以由此推出：

ΔN公式可以由噪声整形原理及式（9）至式（12）推出：

从式（13）可以看出n阶Sigma-Delta调制器最终输出的低次项都被抵消掉了，噪声只剩高次项，具有高通特性，可以进行噪声整形。

2 Sigma-Delta调制器中累加器结构改进

本文对Sigma-Delta调制器中的累加器结构进行改进。改进后的单级累加器细节如图4所示。

图4 改进后的单级累加器细节图

改进后的结构是在每个时钟周期正常输出误差值c的前提下，将32位加法拆成了两个并行的16位加法。具体做法是，将加法的误差也就是低位加法器（sum_3和sum_4）的进位和溢出通过寄存器DFF3放到下次累加过程中补偿，达到整体累加过程中总的数据量不变。输出误差c则主要通过对含有分母DEN因子的累加器进行判断得出。由1.4节中的内容可知，如果分母值DEN大于或等于累加结果值则C值为1’b0，相反如果DEN值小于累加结果值则C值为1’b1，具体电路中可以通过分母值与累加结果相减，然后通过判断符号位的方式得出C值。同理，拆分后的电路也可以通过减法的形式得出正确的C值，通过高位比较和低位比较相结合的方式，最终得出C值。通过上述处理，在整个过程中达到与32位加法相同的效果。关键伪代码如下所示。

其中，cin对上次输出结果进行补偿，cin[0]为低位相加时的进位；cin[1]为低位减法器的符号位，如果cin[1]为1，则表明本次反馈回来的低位是负数的补码，即向高位借位相减后的结果，所以高位需要减去cin[1]；co_m是低位相加产生的进位，co_s是低位相减后的符号位，cmp_eq是高位是否相等的判断结果，co是输出的用于补常的数据。

3 仿真结果与分析

3.1 仿真结果总结分析

通过Verilog HDL硬件语言对改进后的结构进行描述，使用Synopsys VCS工具对改进后结构和传统结构的输出进行了对比验证，并且通过Design Compiler工具基于0.11μm CMOS工艺完成了逻辑综合。

Synopsys VCS工具仿真对比的部分截图如图5（a）和图5（b）所示。可以看到，改进后的结构每级输出中多了2位寄存器数据co，用于补偿本次累加器的输出；改进后的结构与传统结构最终输出的delta_n一致，说明改进后的结构能同位替换传统结构。

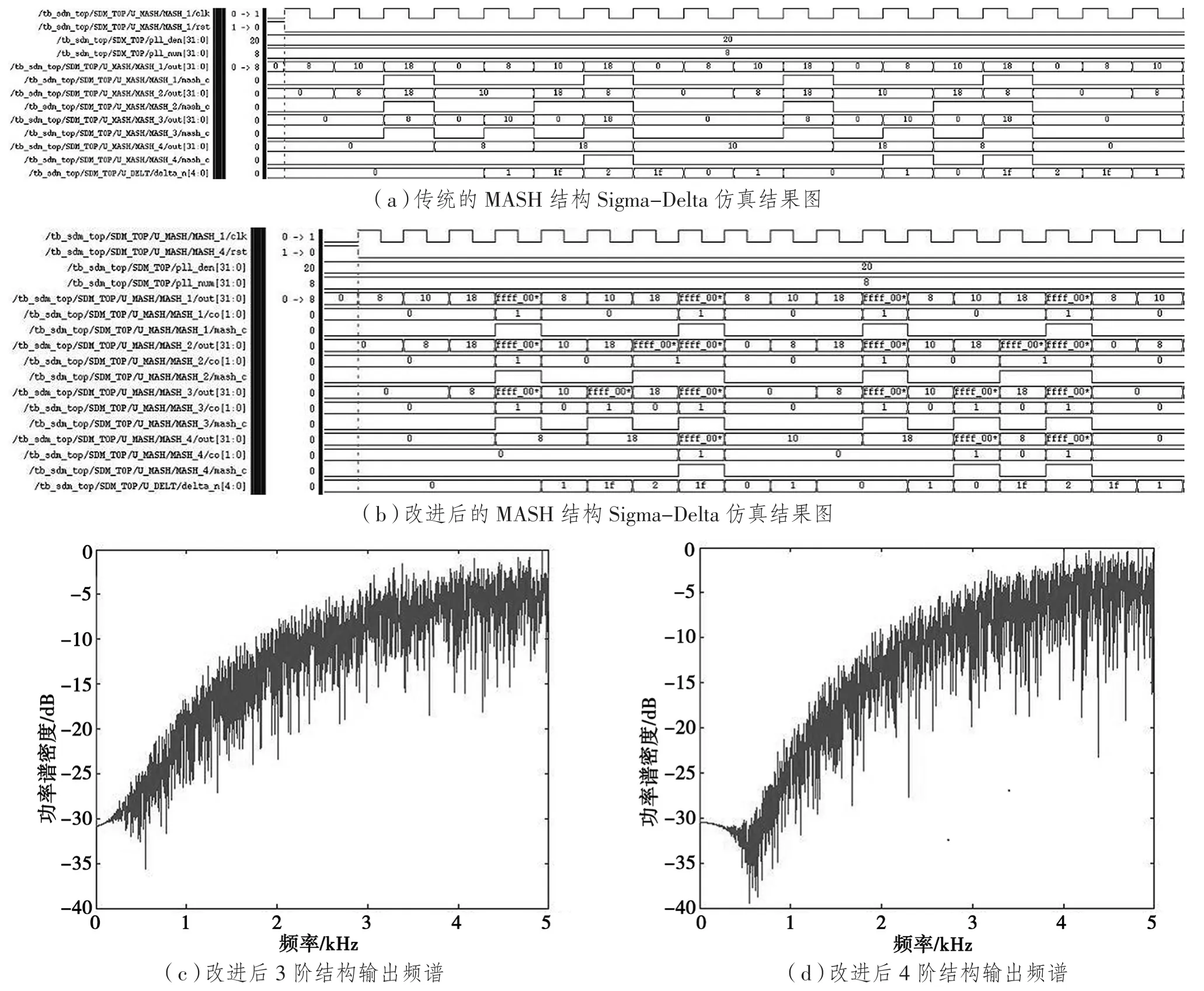
图5 改进前后输出对比

综合结果显示，传统结构四级级联SS-coner下只能达到325 MHz，在同样约束条件下，改进后的结构四级级联SS-coner能达到400 MHz，相比传统结构速度提升了23.77%。传统结构综合后面积为36 827.520 6 μm2，改进后的结构综合后面积为37 930.560 5 μm2，面积相比传统结构多了2.99%。

图5（c）和图5（d）分别为对改进后的MASH 3阶结构和MASH 4阶结构的输出进行频谱分析的结果。可以看出Sigma-Delta调制器将噪声推向高频的特性，与1.3节中Sigma-Delta噪声整形的理论相符，达到了噪声整形的目的。

3.2 不同文献对比

不同文献中Sigma-Delta调制器的设计参数及锁相环输出频率对比如表1所示，可以看出，相比本设计而言，其他小数分频的分频精度相对较低，输出频率范围较窄，对速度要求不是很高。当锁相环输出频率较高时，本设计中的Sigma-Delta调制器将会有较突出的优势。

表1 不同小数分频锁相环设计参数对比

4 结 语

本文针对高速高精度小数锁相环，设计了一款高速Sigma-Delta小数分频器，并通过Verilog HDL语言进行了实现，使用DC综合工具基于0.11 μm CMOS工艺进行了综合，使用VCS工具对设计进行了验证。最终结果显示，本文设计的Sigma-Delta调制器能够实现噪声整形的目的，且相比传统四级结构的Delat-Sigma调制器，在增加2.99%面积的情况下，速度提升了23.77%。