BR0代数的犹豫模糊滤子与理想

彭家寅

PENG Jiayin

内江师范学院 数学与信息科学学院，四川 内江 641199

School of Mathematics and Information Science,Neijiang Normal University,Neijiang,Sichuan 641199,China

1 引言

现实世界中存在着许许多多的不确定型与不精确问题，而建立在Contor集合论上的经典数学工具却很难甚至无法处理这类问题。1965年，Zadeh对Contor的集合进行了推广，提出模糊集理论[1]，在某种程度上有效地解决了一些不确定问题。随后，模糊集理论得到了迅速发展，研究者们提出了直觉模糊集理论[2]、vague理论[3]、区间数理论[4]等等作为数学工具来处理嵌入在系统中不同类型的不确定性和不精确性问题，丰富和发展了经典的模糊集理论。然而，这些理论都存在一定的局限性[5]，在较多决策问题中，许多决策者在做决策时常常是犹豫的，在几个可能方案之间徘徊，并且不同决策者的可能方案数目通常是不同的，像这样的问题用上述理论模型很难准确描述。为此，Torra[5]引入了犹豫模糊集，从一个新的角度扩展了Zadeh经典模糊集理论，它允许其元素的隶属度有多个可能值。犹豫模糊集引起了国内外研究者们的浓厚兴趣，其理论与应用得到了快速发展[6-14]。

1993年C.Elkan博士在美国第十一届人工智能年会上的一篇报告“模糊逻辑似是而非的成功”引起了学者们关于模糊逻辑的意义和应用的一场激烈的争论。这场争论的各方都或多或少，有意无意地触及到了模糊控制的核心“部件”——“模糊推理”。为了将模糊推理纳入到严格的逻辑框架之中，王国俊教授[15]建立了一种模糊命题演算的形式演绎系统L∗和与之在语义上相匹配的R0代数。吴洪博教授在此基础上提出了基础L∗系统和基础R0代数，即BL∗系统和BR0代数[16]，文献[17-18]进一步探究基础L∗系统和基础R0代数问题。从文献[16-18]可以看出MV代数是BR0-代数的特例，Lukasiewicz模糊命题演算系统是BL∗系统的扩张，并且BR0代数与Hajek[19-20]提出的BL代数有本质的不同，这就意味着对BR0代数的研究是很有意义的工作。众所周知，滤子理论与理想理论在逻辑代数系统的结构研究中扮演着十分重要的角色。文献[21]引入了BR0代数的模糊滤子与模糊素滤子的概念，研究了其相关性质。文献[22]提出了BR0代数的模糊理想和模糊素理想的概念，研究了它们的基本性质，给出了BR0代数的模糊集构成模糊理想的条件。本文，将犹豫模糊集应用于BR0代数中，建立拟BR0代数的犹豫模糊滤子与理想理论，研究其性质和结构特征。

2 预备知识

定义1[5]设X为一个给定的集合，一个X上的犹豫模糊集的定义如下：

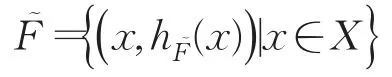
其中是由区间[0，1]上若干个不同值构成的集合，表示X中的元素x属于集合的若干种可能隶属度。

设为X上的犹豫模糊集，P([0,1])为区间[0,1]的幂集。称集合

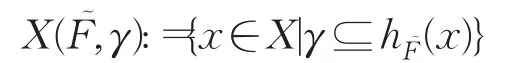
为犹豫水平集，其中γ∈P([0,1])。

定义2[16]设 X是(¬,∨,→)型代数，如果 X 上有偏序≤使(X,≤)成为有界分配格，且∨是关于序≤的上确界运算，¬是关于序≤的逆序对合对应，且

其中1是(X,≤)的最大元，则称X为基础R0代数，记为BR0代数，并记0=¬1。以下用符号'表示¬，并在BR0代数 X 中引入圈乘运算：⊗:x⊗y=(x→y′)′，可以证明圈乘运算⊗和蕴涵算子→构成伴随对。

定义3[23]设X为BR0代数且F⊆X，称F为X的滤子，如果对任意x,y∈X，有

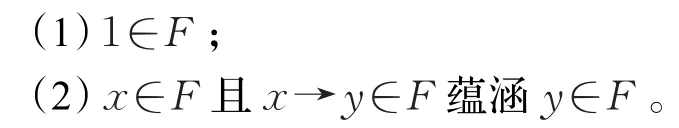
若F为X的滤子且F≠X，则称F为X的真滤子。

定义4[23]设X为BR0代数且I⊆X，称I为X的理想，如果对任意x,y∈X，有

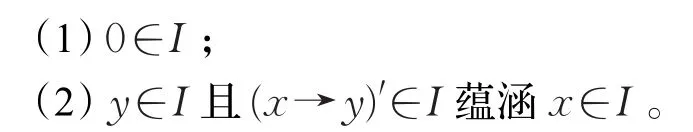
若I为X的理想且1∉I，则称I为X的真理想；进一步，当 x∧y∈I有 x∈I或 y∈I，则称I为X的素理想。

3 BR0代数的犹豫模糊滤子

定义5BR0代数X上的一个犹豫模糊集叫作X的一个犹豫模糊滤子，如果它满足

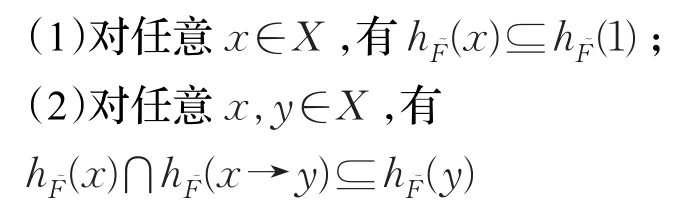
设为X的一个犹豫模糊滤子，若存在x∈X使得，则称为 X 的一个犹豫模糊真滤子。

定理1设为BR0代数X的一个犹豫模糊滤子，如果 x,y∈X 使得 x≤y ，那么。

证明设 x,y∈X使得 x≤y，则 x→y=1。由为 X 的一个犹豫模糊滤子，所以

定理2设为BR0代数X的犹豫模糊真滤子，则

证明若，因1是X 的最大元及¬为逆序对合的，故对任意 x∈X ，x′≤1，0=1′，进而 x′→1=1，

0′=1 。由定理1和定义5（2）可以得知，。结合定义 5（1）有，，这与为 X 的犹豫模糊真滤子矛盾，所以。

定理3设为BR0代数X上的犹豫模糊集，则为X的犹豫模糊滤子的充要条件是对任意γ∈P([0,1])，当时，X,γ)为 X 的滤子。

证明假设为X的犹豫模糊滤子，γ∈P([0,1])且，则存在 x∈X 使得。由定义5（1）知，，故 γ ⊆ h(1)，即。假设且，则且。由定义5（2）知，。按定义3，X(,γ)为 X 的滤子。

反之，假设对任意 γ∈P([0,1])，当时，X(,γ)为 X 的滤子。对任意 x∈X ，记，则 x∈X(,γ)且 X(,γ)为 X 的滤子。于是 1∈X(,γ)，也就是，即定义5（1）成立。对任意 x,y ∈X ，记，，则

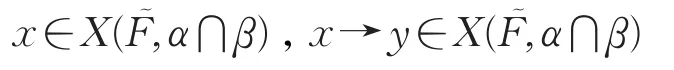
且为 X 的滤子。由定义3可知，y∈X(,α⋂β)，进而

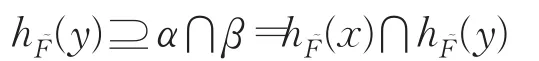
即定义5（2）成立。综上所述，为X的犹豫模糊滤子。

推论1设为BR0代数X的犹豫模糊滤子，则为 X 的滤子。

推论2设为BR0代数 X的犹豫模糊滤子且a∈X ，则为 X 的滤子。

推论3设A为BR0代数X的滤子，且α,β∈P([0,1])使得α⊂β。定义X上的犹豫模糊集如下：

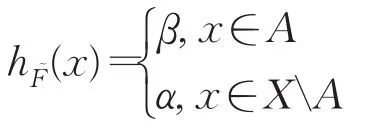
则为X的犹豫模糊滤子。

定理4设和为BR0代数X的犹豫模糊滤子，则⋂是X的犹豫模糊滤子。

证明对任意x∈X，

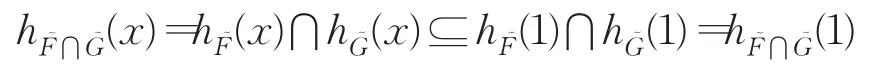
又任意x,y∈X，都有：

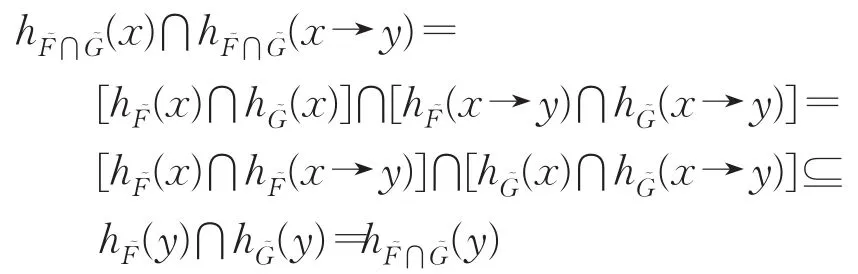
所以⋂是X的犹豫模糊滤子。

定义6设X和Y都是BR0代数，f是BR0代数X到BR0代数Y的同态映射，与分别是X和Y上的犹豫模糊集，则由 f可诱导出两个犹豫模糊集f()和 f-1()：

注：hf()的定义等价于：对于任意

定理5设X和Y都是BR0代数，f是BR0代数X到BR0代数Y的同态映射。

（1）若为X的犹豫模糊滤子，且 f是同构映射，则 f()为Y的犹豫模糊滤子。

（2）若为Y 的犹豫模糊滤子，则 f-1()为 X 的犹豫模糊滤子。

证明（1）∀y∈Y ，因 f同构，故

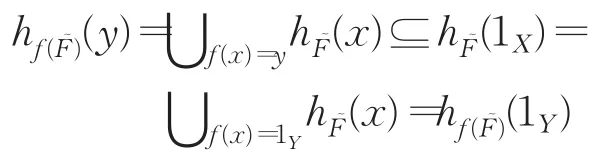
这里1X和1Y分别是X和Y中的最大元。对任意y1,y2∈Y，因 f为同构映射，所以分别存在 x1,x2∈X使得f(x1)=y1，f(x2)=y2。于是 f(x1→x2)=y1→y2，故

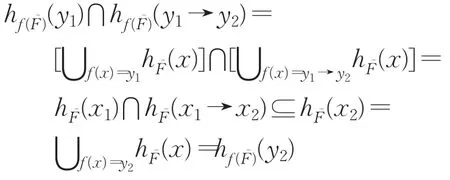
所以 f()为Y的犹豫模糊滤子。

（2）因 f为同态映射，f(1X)=1Y。对任意x∈X都有，。对任意 x1,x2∈X ，令 f(x1)=y1，f(x2)=y2，则 y1,y2∈Y且

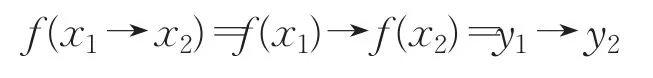
故

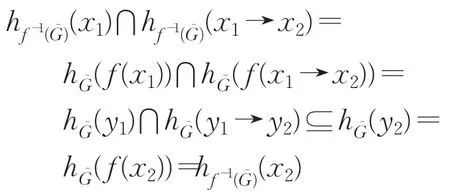
所以 f-1()为X的犹豫模糊滤子。

4 BR0代数的犹豫模糊理想

定义7设为BR0代数X的犹豫模糊集，称为X的犹豫模糊理想，如果它满足

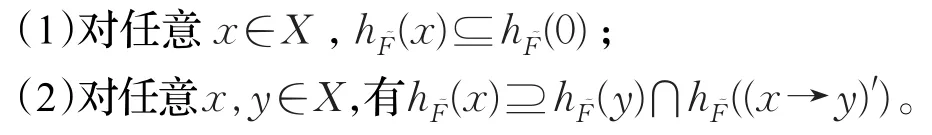
设为 X的犹豫模糊理想，若存在 x∈X使得，则称为 X 的犹豫模糊真理想。

定理6设为BR0代数X的犹豫模糊理想，若x,y∈X 使得 x≤y ，则。

证明设 x,y∈X 且 x≤y，则 x→y=1。又为X的犹豫模糊理想，依定义7有：

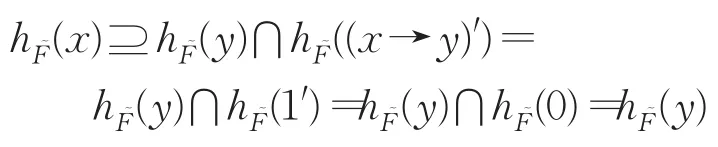
所以结论成立。

定理7设为 X的犹豫模糊真理想，则

证明若，则对任意 x∈X ，由定义 7知 ，h(0)=h(0)，结合定义7（1）知，h(x)=h(0)对任意 x ∈X都成立，这与为X的犹豫模糊真理想矛盾，所以h(1)≠h(0)。

定理8设为BR0代数X的犹豫模糊集，则为X的犹豫模糊理想的充要条件是：对任意γ∈P([0,1])，当 X(,γ)≠∅ 时，X(,γ)为 X 的理想。

证明假设为X的犹豫模糊理想，γ∈P([0,1])且 X(,γ)≠∅ ，则存在 x∈X 使得 h(x)⊇ γ ，由定义7（1）知，h(0)⊇ h(x)⊇γ ，所以 0∈X(,γ)。假设 y∈X(,γ)，(x → y)′∈ X(,γ)，则 h(y)⊇ γ 且 h((x → y)′)⊇γ 。 由 定 义 7（2）知 ，h(x)⊇ h(y) ⋂h((x → y)′)⊇γ⋂γ=γ ，所以 x∈X(,γ)，因此 X(,γ)为 X 的理想。

反 之 ，设 任 意 γ∈P([0,1])，当 X(,γ)≠∅ 时 ，X(,γ)为 X 的理想。对任意 x∈X ，记 h(x)=γ ，则x∈X(,γ)且 X(,γ)为 X 的理想。由定义 4（1）知，0∈X(,γ)，于是 h(0)⊇γ=h(x)，即定义 7（1）成立。对 任 意 x,y∈X ，记 h(y)=α ，h((x→y)′)=β ，则y∈X(,α⋂β)且 (x→y)′∈ X(,α⋂β)。因 X(,α⋂β)为 X 的理想，则 x∈ X(,α⋂β)，从而 h(x)⊇α⋂β=h(y)⋂ h((x → y)′)，即定义7（2）成立。综上所述，为X的犹豫模糊理想。

推论4设I为BR0代数X的理想，且α,β∈P([0,1])使得α⊂β。定义X上的犹豫模糊集如下：

则为X的犹豫模糊理想。

推论5设为BR0代数X的犹豫模糊理想，则{x ∈ X|h(x)=h(0)}为 X 的理想。

推论6设为BR0代数 X的犹豫模糊理想且a∈X ，则 {x∈X|h(a)⊆h(x)}为 X 的理想。

定理9设和都是BR0代数X的犹豫模糊理想，则⋂也是X的犹豫模糊理想。

证明对任意x∈X，有

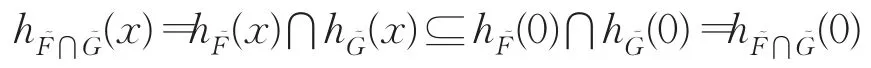
对任意x,y∈X，有

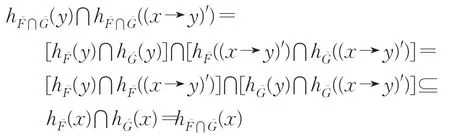
这就表明⋂是X的犹豫模糊理想。

注若和都是BR0代数X的犹豫模糊理想，但⋃未必是X的犹豫模糊理想。例如，令X={a,b,c}，则(2X;¬,∨,→)为 BR0代数，其中2X为 X 的幂集，任意A,B⊆X，¬A=X-A，A∨B=A⋃B，A→B=¬A∨B。定义2X的犹豫模糊集和为：

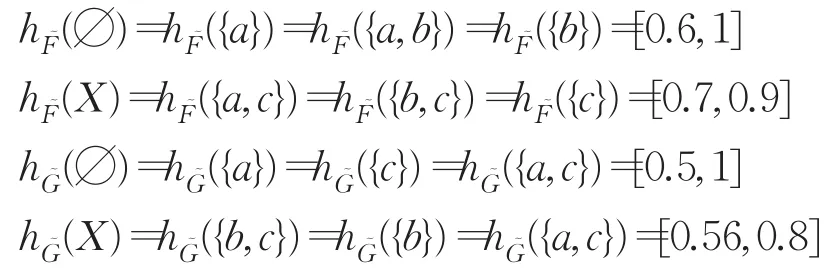
可以验证和都是BR0代数2X的犹豫模糊理想，但⋃不是2X的犹豫模糊理想，这是因为，因此

定理10设X和Y都是BR0代数，f是BR0代数X到BR0代数Y的同态映射。

（1）若为X的犹豫模糊理想，且 f是同构映射，则 f()为Y的犹豫模糊理想。

（2）若为Y 的犹豫模糊理想，则 f-1()为 X 的犹豫模糊理想。

证明（1）对任意y∈Y，总有

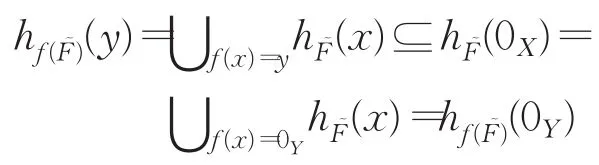
这里0X∈X，0Y∈Y。又对任意y1,y2∈Y，因为 f为同态映射，所以存在x1,x2∈X使得f-1(y1)={x1}，f-1(y2)={x2}并且

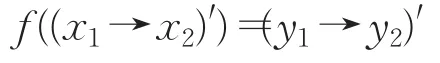
于是

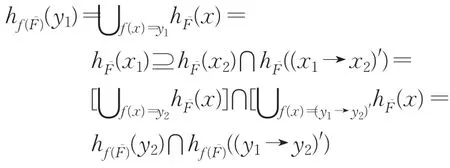
所以 f()为Y的犹豫模糊理想。

（2）因f为同态映射，所以f(0X)=0Y。对任意x∈X,有即定义7（1）成立。对任意x1,x2∈X，因为Y的犹豫模糊理想，故因 f是同态映射，所以

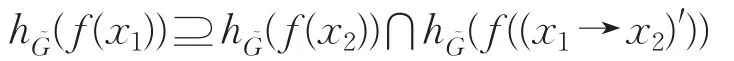
按照定义6关于犹豫模糊集 f-1()的定义知，。 综 上 所 述 ，f-1()为X的犹豫模糊理想。

定义8设为BR0代数X的犹豫模糊真理想，如果满足：对任意 x,y∈X ，都有 h(x∧y)⊆h(x)⋂h(y)，则称为 X 的犹豫模糊素理想。

定理11设为BR0代数X的犹豫模糊真理想，则为X的犹豫模糊素理想的充要条件是：对任意x,y ∈ X ，有 h(x ∧y)=h(x)⋂ h(y)。

证明充分性：显然成立。

必要性：由定义8知，h(x∧y)⊆ h(x)⋂ h(y)对任意x,y∈X成立。又因为X的犹豫模糊理想，依定理6知，h(x ∧y)⊇ h(x)且 h(x ∧y)⊇ h(y)，故

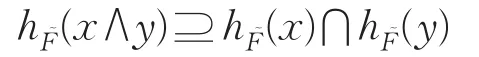
所以

定理12设为BR0代数X的犹豫模糊素理想，则 h(x ∨ y)=h(x ∧ y)。

证明因为X的犹豫模糊素理想，由定义7（2）知，

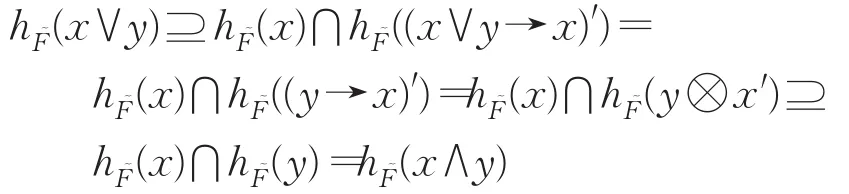
结合定理6有，h(x ∨ y)⊆ h(x)且h(x ∨ y)⊆ h(y)，所以 h(x ∨ y)⊆ h(x)⋂ h(y)=h(x ∧ y)，故 h(x ∨y)=h(x ∧y)。

定理13设为BR0代数X的犹豫模糊素理想，则对任意 γ ∈P([0,1])，当 X(,γ)≠∅ 时，X(,γ)为 X的素理想。

证明因为X的犹豫模糊理想，由定理8知，对任意 γ ∈P([0,1])，当 X(,γ)≠∅ 时，X(,γ)为 X 的理想。设 x∧y∈X(,γ)，则h(x∧y)⊇γ，由定理11知，h(x)⋂h(y)⊇ γ ，故 h(x)⊇ γ 且 h(y)⊇ γ ，即 x ∈ X(,γ)，y∈X(,γ)，因此 X(,γ)是 X 的素理想。

注定理13的逆命题不真。对任意γ∈P([0,1])，当X(,γ)≠∅ 时，X(,γ)为 X 的素理想。由定理8知，为X的犹豫模糊理想。令X={0,a,b,1}，X上的序关系为0≤a≤b≤1，可以证明X为BR0代数。定义X上的犹豫模糊集:X → P([0,1])，满足 h(0)⊃ h(a)⊃ h(b)⊃h(1)，令 γ =h(a)，则 X(,γ)={0,a}为 X 的素理想。但h(a ∧ b)=h(a)⊃ h(b)，所以 h(a ∧ b)⊃ h(a)⋂ h(b)，故为X的犹豫模糊素理想。

定理14设为BR0代数X的犹豫模糊素理想，记 F={x∈X|h(x)=h(0)}，则 F 为 X 的素理想。

证明由推论5知，F为X的理想。设x∧y∈F，则 h(x∧y)=h(0)。因为 BR0代数 X 的犹豫模糊素理想，所以 h(x)∧ h(y)=h(x ∧ y)=h(0)，于是 h(x)⊇h(0)且 h(y)⊇ h(0)。由定义7（1）知，h(x)⊆ h(0)且h(y)⊆ h(0)，因此h(x)=h(0)=h(y)，故 x ∈ F，y ∈ F，这表明F为X的素理想。

类似于定理10的证明，可以得到如下定理。

定理15设X和Y都是BR0代数，f是BR0代数X到BR0代数Y的同态映射。

（1）若为X的犹豫模糊素理想，且 f是同构映射，则 f()为Y 的犹豫模糊素理想。

（2）若为Y 的犹豫模糊素理想，则 f-1()为 X的犹豫模糊素理想。

5 结论

不确定性常常出现在现实世界的许多问题中，模糊集及其扩展为处理这些不同问题的不确定性提供了成功理论与方法。犹豫模糊集就是其中一个为处理犹豫情境下不确定性问题的拓展版，并且已成功地应用于决策问题中，然而用之探究代数结构的文献不多。另一方面，BR0代数中模糊理想理论的研究在技术上是比较困难的，到目前为止研究文献很少。为此，本文将犹豫模糊集应用于BR0代数的理想理论中，引入了犹豫模糊滤子、犹豫模糊理想和犹豫模糊素理想的概念，研究它们基本性质，给出了BR0代数的犹豫模糊集成为犹豫模糊滤子、犹豫模糊理想和犹豫模糊素理想条件。说明了犹豫模糊素理想的任何非空子集是素理想，但反之不然。证明了犹豫模糊滤子、犹豫模糊理想及犹豫模糊素理想在交运算及BR0代数同构运算下的不变性。用犹豫模糊集去研究BR0代数结构的这一思想方法，也可以用于研究MV-代数、格蕴涵代数、MTL-代数、Heyting代数、BCK-代数等逻辑代数结构，乃至群、环、域等一般代数结构讨论中。

参考文献：

[1]Zadeh L A.Fuzzy sets[J].Information and Control，1965，8：338-353.

[2]Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20（1）：87-96.

[3]Gau W L，Buehrer D J.Vague sets[J].IEEE Transactions on Systems，Man，and Cybernetics，1993，23（2）：610-614.

[4]Zadeh L A.The concept of a linguistic variable and its application to approximate reasoning[J].Information Sciences，1975，8（2）：199-249.

[5]Torra V.Hesitant fuzzy sets[J].International Journal of Intellignt Systems，2010，25：529-539.

[6]Xu Z S，Xia M M.Distance and similarity measures for hesitant fuzzy sets[J].Information Sciences，2011，181：2128-2138.

[7]Chen N，Xu Z，Xia M M.Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis[J].Applied Mathematical Modelling，2013，37：2197-2211.

[8]Xia M M，Xu Z S.Hesitant fuzzy information aggregation in decision making[J].International Journal Approximate Reasoning，2011，52：395-407.

[9]Yu D，Wu Y，Zhou W.Generalized hesitant fuzzy geometric Bonferroni mean and its application in multi-criteria group decision making[J].Journal of Information&Computational Science，2012，9：267-274.

[10]Zhang Z M.Hesitant fuzzy power aggregation operators and their application to multiple attribute group decision making[J].Information Sciences，2013，234：150-181.

[11]Yue L，Sun M，Shao Z.The probabilistic hesitant fuzzy weighted average operators and their application in strategic decision making[J].Journal of Information&Computational Science，2013，10：3841-3848.

[12]Bedregal B，Reiser R，Bustince H，et al.Aggregation functions for typical hesitant fuzzy elements and the action of automorphisms[J].Information Sciences，2014，255：82-99.

[13]Qian G，Wabg H，Feng X.Generalized of hesitant fuzzy sets and their application in decision support system[J].Knowledge-Based Systems，2013，37：357-365.

[14]Ye J.Correlation coefficient of dual hesitant fuzzy sets and its application to multiple attribute decision making[J].Applied Mathematical Modelling，2014，38：659-666.

[15]王国俊.数理逻辑引论与归结原理[M].2版.北京：科学出版社，2006.

[16]吴洪博.基础R0代数与基础L∗系统[J].数学进展，2003，32（5）：565-576.

[17]胡明娣，王国俊.基础代数的结构研究[J].纺织高校基础科学学报，2006，19（3）：205-209.

[18]吴洪博，文秋梅.基础L∗系统的一种扩张——Lukasiewicz系统[J].模糊系统与数学，2002，16（2）：52-57.

[19]Hajek P.Metamathematics of fuzzy logic[M].Dordrecht，The Netherlands：Kluwer Academic Publishers，1998.

[20]Hajek P.Basic fuzzy logic and BL-algebras[J].Soft Computing，1998，2：124-128.

[21]龚加安，吴洪博.BR0代数的模糊滤子与模糊素滤子[J].安康学院学报，2009，21（6）：91-93.

[22]李海霞，张修彦，吴洪博.BR0代数的Fuzzy理想与Fuzzy素理想[J].纺织高校基础科学学报，2008，21（1）：1-3.

[23]程国胜.R0代数中的滤子与理想[J].模糊系统与数学，2001，15（1）：58-61.