基于云模型的不确定性大群体多属性决策方法

肖子涵，耿秀丽，徐士东

XIAO Zihan,GENG Xiuli,XU Shidong

上海理工大学 管理学院，上海 200093

Business School,University of Shanghai for Science and Technology,Shanghai 200093,China

1 引言

随着社会经济的发展和环境的复杂性加剧，规划、战略等决策问题需要大量人员共同参与决策过程。在实际决策过程中，由于事物本身的模糊性、决策者自身的局限性和主观性等特征，决策者很难对决策对象进行精确的评价，因此，不确定性大群体决策问题越来越受到人们的重视。

文献[1]针对决策偏好为区间直觉梯形模糊数的大群体决策冲突测度问题，提出了聚集冲突测度模型并集结为群体冲突测度模型，然后应用于大群体偏好集结。文献[2]将直觉模糊熵与TOPSIS相结合确定综合权重，应用于应急大群体决策。现有方法只考虑到决策信息的模糊性，却没有考虑到随机性，而决策信息的随机性在不确定性大群体多属性决策中是普遍存在的。随机性是不确定性概念的另一个重要性质，云模型是李德毅院士于1995年在概率论和模糊数学基础上提出的概念，它同时研究了模糊性和随机性以及两者之间的关联性，更好地刻画了自然语言中概念的不确定性[3-4]，同时也更好地克服了定性与定量转换过程中的信息缺失问题。

云模型间的差异化度量是方案排序和优选过程中的重要内容。文献[5]提出一种基于前景理论和云模型的决策方法，在最优权系数基础上，通过各方案综合前景值进行排序。文献[6]利用云模型云滴的随机性和稳定倾向性的特点，提出了一种云模型云滴机制的量子粒子群优化算法。文献[7]针对专家权重未知，评价值为不确定语言的多准则群决策问题，基于综合云，通过Hamming距离求得贴近度大小，进而对备选方案进行排序。以上研究只是从云模型的数字特征出发对云模型进行的简单比较，然而云是由一定数量符合一定随机规则的云滴构成的，这就使得数字特征都相同的云其云滴也不完全相同，因此单纯通过数字特征的计算来确定云的距离不够合理和精确。文献[8]从云滴分布的角度，基于云滴之间的横坐标差值，提出云的相似度算法。文献[9]提出基于云模型最大最小贴近度和算术平均最小贴近度的两种云的相似度算法。以上研究只是通过云滴的横坐标比较和度量来进行相似度计算，没有考虑云滴纵坐标对计算结果的影响，使得计算结果不够精确合理，基于此，本文通过计算云滴的距离，并基于云的距离测度对云的相似度算法进一步改进，提出了一种改进的云相似度算法，采用云的相似度来实现云模型间的差异化度量并最终实现方案排序。

专家权重的确定是大群体决策中的又一关键问题。在专家权重确定过程中，由于专家具有不同的知识、经历和偏好，应该首先对专家进行聚类。由于所提供评价信息存在差异性，因此聚类后专家评价信息的一致性程度越高表示该小群体越重要。文献[10]针对决策者主观权重已知，提出一种通过计算专家个体决策结果与群体决策结果的偏差量并结合熵理论求得专家的客观权重的权重调整算法。文献[11]利用二元语义集成算子计算属性的主观权重，基于最小偏差确定属性客观权重，主客观相结合解决属性值和属性权重信息均以语言评价信息形式给出的多属性群决策问题。本文针对已知专家聚类的大群体决策问题，研究基于小群体权重的多属性决策问题，假设小群体中专家无差别，提出主客观相结合确定小群体权重的方法，主观权重由决策者根据小群体的重要度来确定，客观权重由基于对各决策指标评价信息的一致性分析来确定。

本文提出基于云模型的大群体决策方法，首先采用云模型将专家的对备选方案的语言评价值进行云量化；然后采用决策者主观确定和一致性分析相结合的主客观权重确定方法确定小群体权重，合成得到方案综合云；最后基于云的距离测度提出了一种改进的云相似度算法，通过云的相似度算法比较各方案综合云并最终实现方案的排序。

2 基于云模型的决策信息转化

2.1 云模型的基本概念

李德毅院士在1995年提出了一种能将定性语言值转化为数值描述的不确定定量模型——云模型[12]，该模型将模糊性和随机性结合在一起，构成定性和定量之间的映射。

定义1[13]设U是一个数值表示的定量论域，C是论域U上的定性概念，存在定量值x∈U是定性概念C上的一次随机实现，且对C的隶属度μ(x)∈[0 ,1]是一个具有稳定倾向的随机数，即 μ:U→[0 ,1]，∀x∈U ，x→μ(x )，则隶属度 μ(x)在论域U上的分布简称为云，记为C(U )，且每一个(x,μ(x))称为一个云滴。

云模型用期望Ex，熵En，超熵He来表示定性的概念，其中Ex表示定性语言概念论域的中心值，熵En代表定性概念不确定度的度量，超熵He代表熵的离散程度，因此，也将云记为C(Ex,En,He)[14]。

定义2[15]设在论域U中有n朵基云{C1(Ex1,En1,He1)，C2(Ex2,En2,He2),…,Cn(Exn,Enn,Hen)}，可将n朵云集成一朵综合云C(Ex,En,He)。

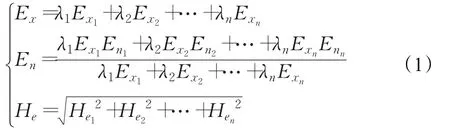
其中λ=(λ1,λ2,…,λn)为 n 朵云权重值。

2.2 评价语言值转化为云模型

设决策者对各方案属性的语言评价等级为n（一般为奇数），由专家制定有效论域U=[Xmin,Xmax]，利用黄金分割法生成n朵云与相应的语言标度一一对应。一般情况下，中间的一朵云为C0(Ex0,En0,He0)，左右相邻的云分别为，中间的云用来表示一般或中等的定性概念的完整云，左边的云是用来表示较差或差等一些定性概念的半降云，右边的云是用来表示较好或好等一些定性概念的半升云[16]。

在有效论域中可用黄金分割法生成n朵云。黄金分割法生成5朵云的计算方法如表1所示。

2.3 云的相似度

在文献[8]提出的云相似度算法基础上，基于云的距离计算提出改进的云相似度算法。

输入：两个云模型C1=(Ex1,En1,He1)、C2=(Ex2,En2,He2)和云滴数n。

表1 黄金分割法生成云的计算方法

输出：两个云模型间的相似度Sim(C1,C2)。

步骤1两朵云C1=(Ex1,En1,He1)、C2=(Ex2,En2,He2)通过云发生器各生成n个云滴。

步骤2将各自云滴按横坐标从小到大进行排序。

步骤3对云滴进行筛选，保留落在[Ex-3En,Ex+3En]范围内的云滴。

步骤4设筛选后的两朵云的云滴数分别为n1和n2，假设n1≥n2，将第一朵云从n1个云滴中随机选取n2个云滴，对云滴按横坐标从小到大进行排序，保存在集合Drop1和Drop2中，若n1＜n2，则与此类似。

步骤5将两个集合Drop1、Drop2按对应的次序计算各云模型C1、C2之间的距离d(C1,C2)：

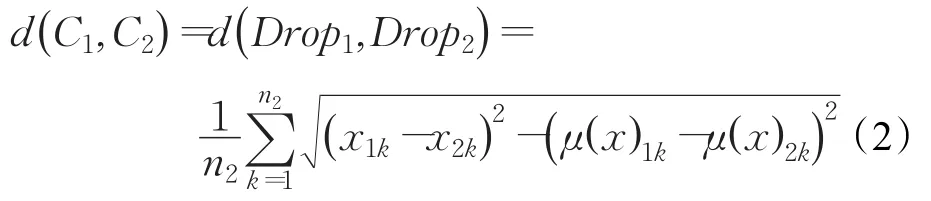
步骤6基于云的距离计算结果计算云的相似度Sim(C1,C2)：

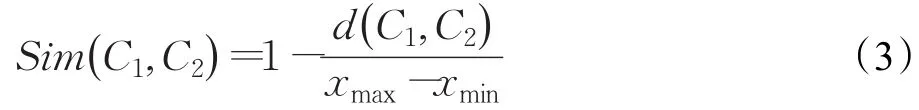
算法中步骤4是指如果筛选出的云滴数不一致，以较少的云滴数作为统一的云滴数，这是因为根据“3σ规则”在[Ex-3En,Ex+3En]范围内的云滴占据了所有云滴中的绝大部分，两个云模型在生成云滴数同为n的情况下筛选出的云滴数n1和n2差别较小，可以忽略不计，因此可以将多余的云滴直接舍弃。步骤5是对两个云模型距离的求解，它等于两个云模型已筛选云滴集合Drop1、Drop2中所对应云滴间的平均距离。步骤6是在云的距离计算基础上对云的相似度进行计算，xmax-xmin表示有效论域的取值范围，云的距离越大其相似度越小，反之，云的距离越小其相似度越大，特殊的，当

上述云的相似度算法是从云滴分布的角度对云模型进行的差异性度量，充分考虑了云模型本身的特点，基于云滴的距离来计算云的相似度比单纯采用云滴的横坐标计算云的相似度更具有合理性和准确性，因此，计算结果也更精确可靠。此外，由于云滴分布的随机性，相似度计算结果也随之具有一定的随机性。

3 基于专家权重确定的云模型方案排序

3.1 专家权重确定方法

设群体Ω由m个已知小群体G=(G1,…,Gi,…,Gm}构成，Q={q1,…,qi,…,qm} 表示 Gi中专家成员数。存在n个候选方案A=(A1,…,Aj,…,An)可供选择，每个专家使用语言评价值S=(S1,…,Sl,…,St}对各方案h个评价指标C=(C1,…,Ck,…,Ch)进行评价，各评价指标属性权重为。

群体Gi的主观权重是决策者根据群体Ω中多个群体G={G1,…,Gi,…,Gm}的重要程度来确定的，考虑到参与决策的多个群体Gi中专家之间的公平性，主观权重可根据群体Gi中参与决策的专家数量确定，即表示为：

且

表示群体Gi中专家er对方案Aj第k个属性的语言评价值，是一个0-1变量，表示群体Gi中专家使用评价值Sl对候选方案各属性进行评价的次数，表示Sl在小群体内部专家评价信息中的分布百分比。则

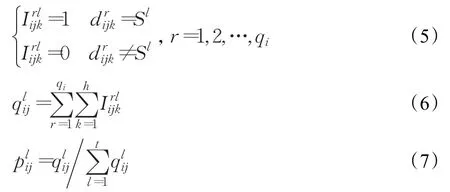
B={B1,…,Bl,…,Bt} 是评价值 S=(S1,…,Sl,…,St}所对应的数集，分布百分比Pij可表示为：

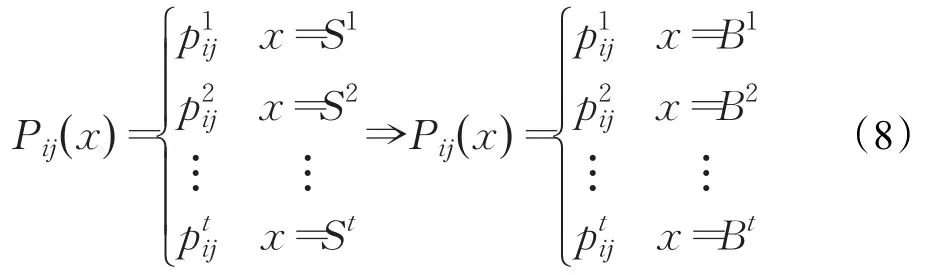
Var(pij)表示百分比 pij的变化，设P∗是一种特殊的分布百分比，Var(P∗)表示理论上百分比的最佳变化，则Var(pij)和Var(P∗)的计算如下：

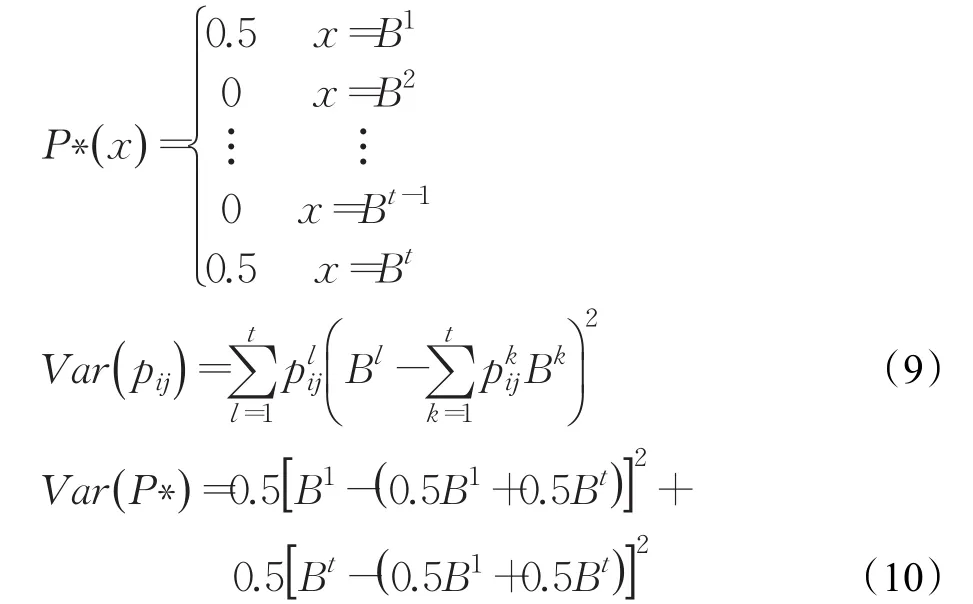
CIij表示群体Gi中专家对方案Aj的h个属性评价的一致性，CIij越高表示群体Gi中专家知识结构和利益需求的一致性程度越高。表示群体Gi针对方案Aj的客观权重，则CIij和的具体计算形式如下：

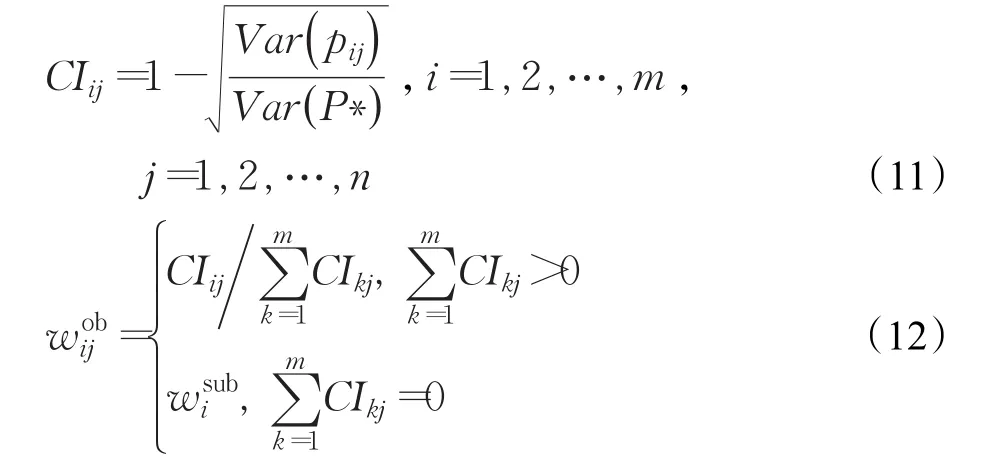
表示群体Gi针对方案Aj的权重，结合主观权重和客观权重，则wij和小群体内部专家权重可表示为：

α、β是参数，0≤α,β≤1，α+β=1，若α=0，则说明在大群体方案评价中只考虑主观权重，若β=0，则说明在大群体方案评价中只考虑客观权重。且0≤wij≤

3.2 基于云模型的方案排序

本文所提基于专家权重确定方法并结合云模型的大群体决策过程如下：

步骤1获取并用语言评价值表达专家对候选方案各属性的评价信息，利用黄金分割法将群体Gi中专家er对方案Aj第k个属性的语言评价值转化为云模型

步骤2根据公式（4）～（14）计算大群体Ω中m个小群体Gi的内部专家权重。

步骤3在云决策矩阵的基础上，根据公式（15）对方案Aj中h个属性的云模型集结为

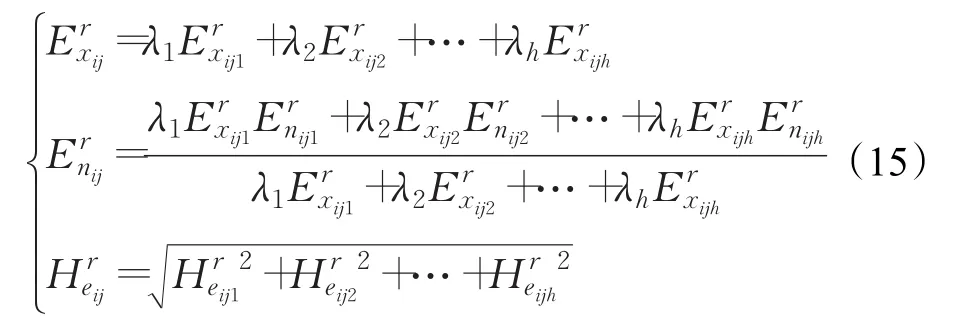
步骤4结合专家权重，根据公式（16）对云模型二次集结为

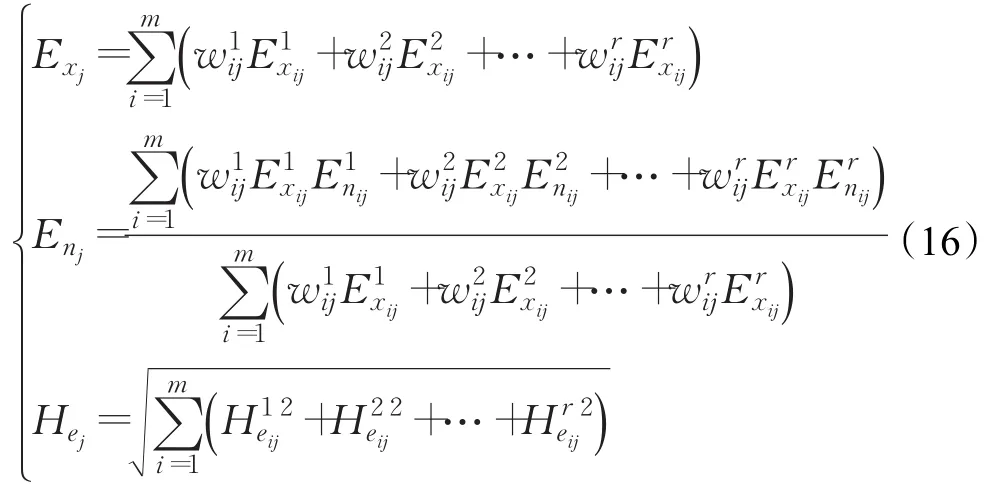
步骤5令C∗=(E x∗,En∗,He∗) 为最优云，依据本文所提云的相似度算法计算Cj与C∗的相似度Sim(Cj,C∗)，按相似度大小对备选方案进行排序。

4 算例分析

随着科技的进步和发展，一系列智能设备的兴起在给人们生活带来极大便利的同时也正在改变着人们传统的生活方式。智能手环是一种具有代表性的可穿戴智能设备，它可以用来监测个人的运动状态和简单生理指标，帮助人们制定运动计划，还可以与智能手机互联，对重要信息进行提示，因此深受用户的喜爱。

某企业是国内一家新兴的智能终端设备研发与制造企业。为了更好地保证其设计产品的竞争力，针对某款智能手环，从屏幕尺寸(C1)、操作方式(C2)、防水级别(C3)、信息提示类型(C4)、待机时长(C5)五方面制定了3个备选设计方案，其具体参数如表2所示。现采用本文所提方法对备选设计方案进行排序并最终确定出最优的设计方案。

表2 备选设计方案指标参数

企业从年纪为 G1：20～30岁、G2：30～40、G3：40～50岁研发人员中分别抽取人数为Q={q1,q2,q3}={15，9，6}组成了30人的专家组对备选设计方案进行评价。预先设定的评估语义集合为：S={S1,S2,S3,S4,S5}={VG，G，F，P，VP}={非常好，好，一般，差，非常差}，决策者对各方案各指标的评价数据如表3所示。根据本文所提的基于云模型的不确定性大群体多属性决策方法对上述备选方案进行选择，具体过程如下。

表3 决策信息表

步骤1给定有效论域U=[Xmin,Xmax]=[0，100]，He0=0.1，根据表1生成5朵云{C+2,C+1,C0,C-1,C-2}与语言评价集 S={VG，G，F，P，VP}对应，其数字特征如表4所示。则表3决策信息表可转化为云决策矩阵

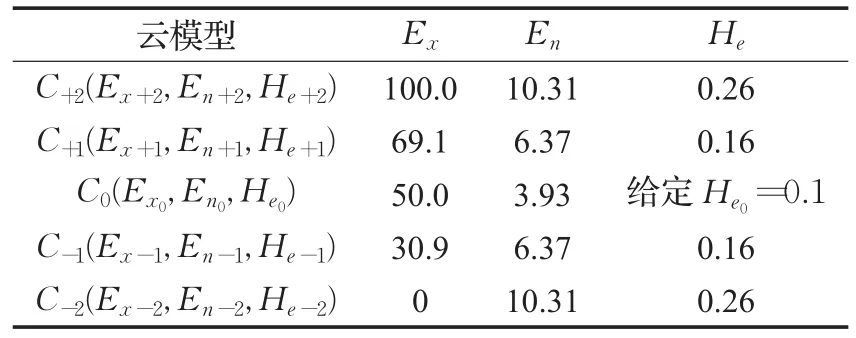
表4 5朵云数字特征

步骤2设定 B=(B1,…,Bl,…,Bt}={1，0.8，0.6，0.4，0.2}是语言评价值 S={VG，G，F，P，VP}所对应的数集，根据公式（4）～（12）计算主观权重和客观权重。

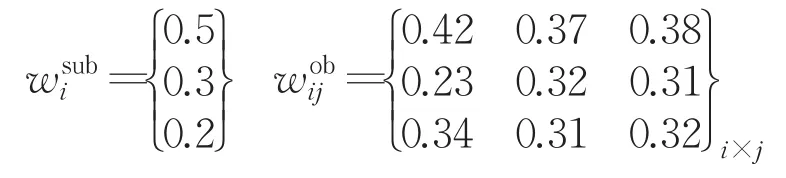
在主客观权重的基础上引入α=0.5，β=0.5，即主客观权重同等重要，根据公式（13）、（14）计算大群体Ω中m个小群体Gi针对方案Aj的权重wij和小群体内部专家权重。

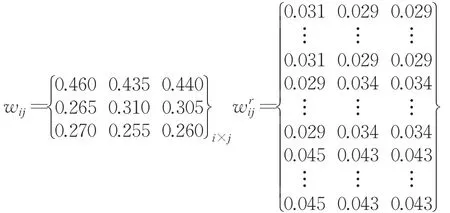
步骤3在云决策矩阵(,,)的基础上，已知 λ=（0.20，0.30，0.12，0.13，0.25），跟据公式（15）对方案Aj中5个属性的云模型集结为如表5所示。

表5 按属性集结后的云模型

步骤4结合小群体内部专家权重，根据公式（16）对云模型二次集结为 Cj(Exj,Enj,Hej)。

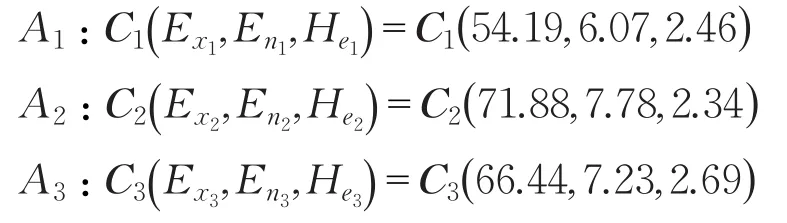
步骤5利用MATLAB生成方案Aj云模型的云图如图1～3所示，令 C*=（100，10.31，0.26）为方案最优云，计算Cj与C*的相似度sim(Cj,C*)分别为：Sim(Cj,C*)={0.357 3，0.599 5，0.534 0}。根据计算结果，备选方案的排序为：A2≻A3≻A1，所以方案A2为最优方案，可以投入生产。

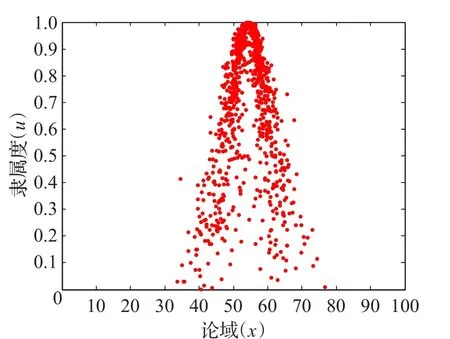
图1 方案A1的云图

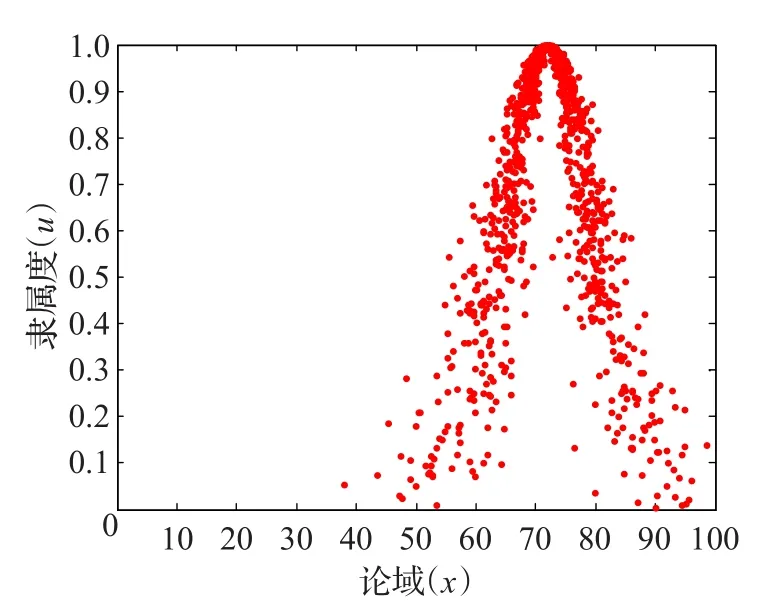
图2 方案A2的云图

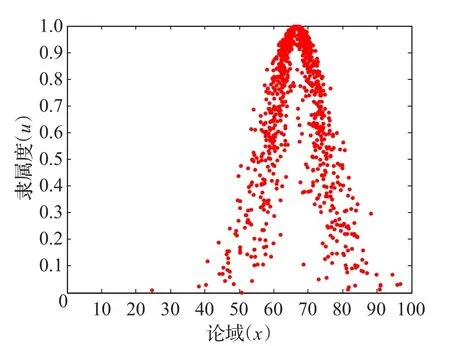
图3 方案A3的云图

5 结束语

本文针对由多个已知小群体组成的大群体，提出了一种基于云模型的不确定性大群体多属性决策方法。针对各决策指标对应的小群体权重不同的问题，提出了主客观权重相结合的方法确定小群体权重。所提方法包括三部分：

（1）采用云模型对专家的语义评价信息进行量化，从评价语言的模糊性和隶属度的随机性两方面更好地刻画了评价过程的不确定性，因此评价结果也更具有客观性和准确性。

（2）在评价信息的基础上，采用决策者主观确定和一致性分析相结合的主客观专家权重确定方法确定小群体权重，在此基础上考虑均等的小群体内部专家权重，结合属性权重和专家权重二次集成生成综合云。

（3）从云滴分布的层面来对云的相似性和差异性进行度量，提出基于云距离测度的云相似度算法并用于确定备选方案与最优云的相似度，进而确定方案的排序，使方案的比较更加准确合理。

所提方法已用于某企业智能手环方案的评价分析，通过实证分析，验证了所提方法的有效性和可行性。

参考文献：

[1]徐选华，万奇锋，陈晓红，等.一种基于区间直觉梯形模糊数偏好的大群体决策冲突测度研究[J].中国管理科学，2014，22（8）：115-122.

[2]王畅，曾亚.基于直觉模糊集的应急决策方法研究[J].情报探索，2016（3）：125-128.

[3]李德毅，孟海军，史雪梅.隶属云和隶属云发生器[J].计算机研究与发展，1995（6）：15-20.

[4]李德毅，刘常昱.论正态云模型的普适性[J].中国工程科学，2004，6（8）：28-34.

[5]赵坤，高建伟，祁之强，等.基于前景理论及云模型风险型多准则决策方法[J].控制与决策，2015（3）：395-402.

[6]齐名军，杨爱红.基于云模型云滴机制的量子粒子群优化算法[J].计算机工程与应用，2012，48（24）：49-52.

[7]王坚强，刘淘.基于综合云的不确定语言多准则群决策方法[J].控制与决策，2012，27（8）：1185-1190.

[8]张勇，赵东宁，李德毅.相似云及其度量分析方法[J].信息与控制，2004，33（2）：129-132.

[9]金璐，覃思义.基于云模型间贴近度的相似度量法[J].计算机应用研究，2014，31（5）：1308-1311.

[10]万俊，邢焕革，张晓晖.基于熵理论的多属性群决策专家权重的调整算法[J].控制与决策，2010，25（6）：907-910.

[11]丁勇，粱昌勇，朱俊红，等.群决策中基于二元语义的主客观权重集成方法[J].中国管理科学，2010，18（5）：165-170.

[12]Li D，Meng H，Shi X.Membership clouds and membership cloud generators[J].Journal of Computer Research&Development，1995，32（6）.

[13]Li D，Cheung D，Shi X，et al.Uncertainty reasoning based on cloud models in controllers[J].Computers&Mathematics with Applications，1998，35（3）：99-123.

[14]Li D Y，Yi D.Artificial intelligence with uncertainty[M].[S.l.]：Chapman&Hall，2005.

[15]王洪利.NSS中基于云模型的谈判人偏好表示及其效用研究[J].中国管理信息化，2008，11（11）：54-58.

[16]王洪利，冯玉强.基于云模型具有语言评价信息的多属性群决策研究[J].控制与决策，2005，20（6）：679-681.