高性能正弦超混沌构造及红外图像安全保护

赵 锋，吴成茂

ZHAO Feng1,WU Chengmao2

1.西安邮电大学 通信与信息工程学院，西安 710121

2.西安邮电大学 电子工程学院，西安 710121

1.School of Telecommunication and Information Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

2.School of Electronics Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

1 引言

红外成像目标探测广泛用于军事战场，它是监视作战环境中的飞机、坦克、装甲车辆等态势的重要手段。近年来，红外成像技术也在海监和反恐等领域得到了一定的应用。如何保护红外成像图像的安全对于作战指挥、海监和反恐等科学决策具有重要作用，已引起了信息安全与对抗专家的高度重视。面对未来作战环境日益复杂，提高红外成像图像的安全是保障现代武器装备发展方向中的综合一体化预警探测系统安全的前提和基础。

针对图像信息所具有的海量性、冗余性和局部相关性等特点，已有大量文献[1]探索了图像信息安全保护措施，特别是混沌映射因具有良好的初始值和参数变化的敏感性而成为解决图像信息安全的重要工具；但是，众多混沌图像加密存在一定安全隐患[2]，难以抵抗选择明文等攻击，从而导致现有混沌图像加密结果安全性差，无法满足军事、海监和反恐等高安全性场合的应用需要。纵观现有混沌图像加密技术，导致其加密结果安全性弱的关键在于：（1）像素位置置乱与像素扩散相互独立；（2）像素值扩散操作非线性差且扩散能力弱；（3）产生密钥的混沌映射本身的复杂性、随机性和敏感性等较弱，无法获得真随机序列。为此，探索新的图像加密机制和方法，提高密文和明文之间的关联性和非线性特性，以及构造超高性能混沌系统产生弱结构随机序列[3]等已成为混沌图像加密研究中的热点方向之一。

在现有众多混沌图像加密算法中，因其存在混沌映射鲁棒性差且难以获得弱结构的随机密钥序列等共性问题[4-6]，本文首先利用正弦函数构造离散二维超混沌系统，该系统Lyapunov指数显著地大于5.0，所产生随机序列具有弱结构性，能较好逼近真随机序列，作为像素扩散操作的密钥序列；其次，将现有像素扩散的异或操作进行拓展并提出参数控制的异或运算与同或运算相混合的像素值扩散机制，以便提高加密结果抗选择明文和差分攻击等能力；最后，鉴于现有图像加密为无意义的噪声，容易引起攻击者或信息对抗方的怀疑[7-8]，将加密图像像素值经非线性变换产生具有一定意义的纹理图像，降低图像加密的怀疑程度，以便进一步提高其安全性，满足军事、国防、海监、反恐等高安全场合的应用需要。

2 二维正弦超混沌系统

针对Logistic混沌映射，因存在稳定窗和空白区而导致其鲁棒性差且混沌行为简单的不足而提出了改进[9]。为了进一步增强Logistic混沌的复杂性和随机性，文献[10]提出了闭环调制耦合的二维Logistic混沌，以及正弦与Logistic函数耦合的二维LASM和SIMM超混沌系统[11-12]。但是，这些二维混沌或超混沌系统不仅其鲁棒性弱，而且它们所对应的最大正李氏指数值明显低于5.0，或者稍微大于5.0且小于6.0，无法产生良好的弱结构随机序列而满足图像加密、混沌信号调制等需要。于是本文将提出具有较强鲁棒性的高性能二维正弦超混沌系统，其两个正李氏指数值都可远大于5.0，能满足混沌系统在众多场合中的应用。

针对文献[12]中正弦函数和闭环调制方法相结合的正弦超混沌系统，即

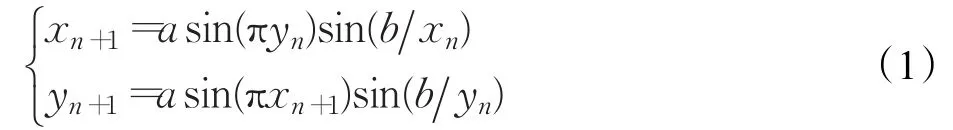
其中a,b＞0。该系统最大正李氏指数值大于5.0且小于6.0，但仍无法产生明显的弱结构随机序列，难以满足高安全性场合图像加密的需要。为此，在文献[13]基于模函数的混沌映射启发下，本文将正弦函数、有限区域模函数，以及闭环调制相结合的高性能超混沌系统定义为：

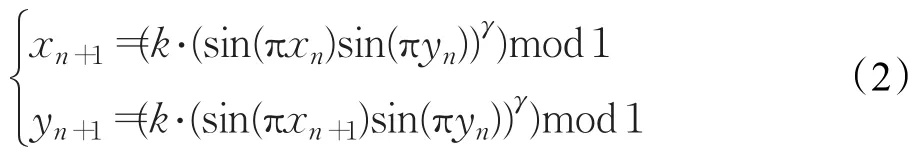
其中k≥1,r＞0且

上述式（2）所获得序列xi,yi(i=0,1,…)的值都属于半开单位区间[0,1)，该超混沌系统所产生的吸引子分布在单位区域[0,1)×[0,1)且具有良好的随机均匀分布特性，从而具有较强的鲁棒性。

针对超混沌系统式（2），有效选取参数k和γ能获得较大正李氏指数，其详细情况如下：

（1）若k=109且0.05＜γ≤1.85时，该系统是超混沌的且最大正李氏指数值大于20。

（2）若k=108且0.22≤γ≤1.71时，该系统是超混沌的且最大正李氏指数值大于19且小于20。

（3）若k=105且0.19≤γ≤1.28时，该系统是超混沌的且最大正李氏指数值大于12且小于13。

（4）若k=103且0.44＜γ≤0.99时，该系统是超混沌的且最大李氏指数值明显大于8.0且小于8.1。

从图1所示来看，本文所建议的二维正弦混沌系统是超混沌的，参数k取值越大则参数γ的有效范围越宽，这表明该系统参数γ与参数k紧密相关，参数γ的有效范围可视为参数k的单调递增函数。另外，该超混沌系统相比最近文献[12]的正弦超混沌系统能获得更大的最大正李氏指数值，对初始参数更加敏感，有利于改善混沌图像加密系统的密钥敏感性等需要。

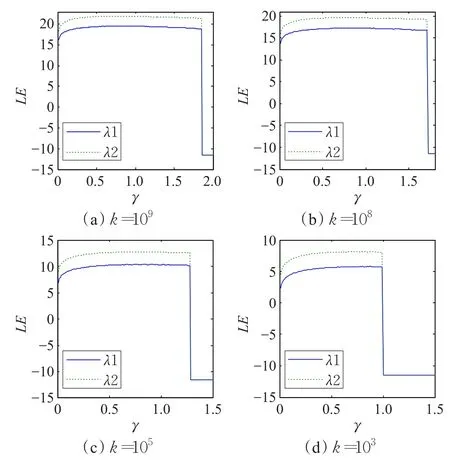
图1 正弦超混沌系统式（2）的李氏指数曲线

针对本文所建议的混沌系统式（2），若选取参数k=108且γ=1.5，以及初始值 x0=y0=0.000 1时，则该系统是混沌的且迭代5 000次所对应的相图如图2（a）所示。若k=109且γ=1.7时，则该系统是超混沌的且迭代所对应的相图如图2（b）所示。从图2所示的正弦超混沌系统相图来看，若式（2）选取适当参数，则该系统是超混沌的，其相空间在单位平面[0，1）×[0，1）上呈均匀分布状态，克服了传统Logistic映射存在稳定窗和空白区的缺陷，表明该系统具有良好的鲁棒性和随机性，利用它产生的加密密钥具有更好的多样性、随机性和安全性。

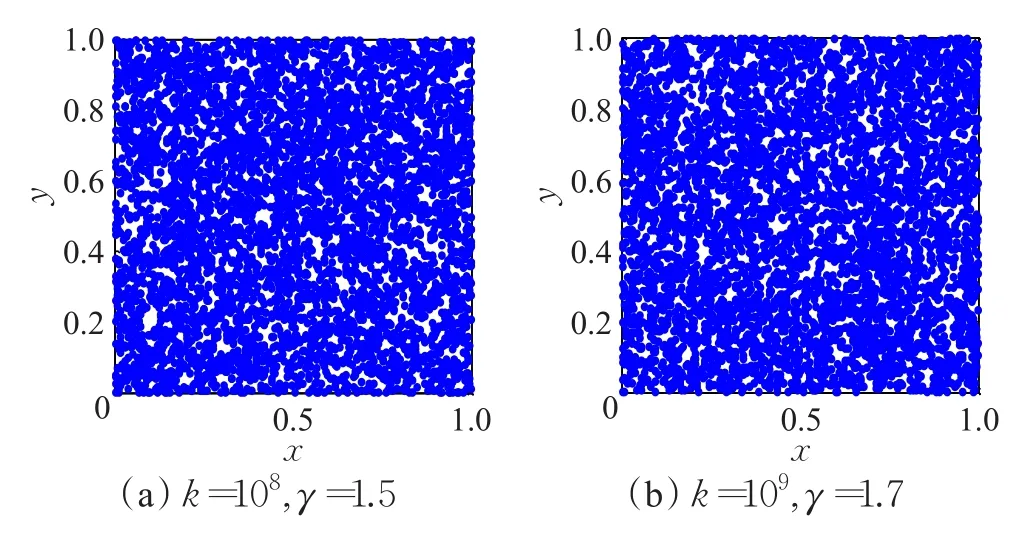
图2 本文建议正弦超混沌系统的相图

针对文献[12]提出的超混沌系统式（1），系统输出保持在单位区间内，必须选取参数a=1。若a=1且b选取任意大于1的正数时，其相图形状变化不明显且相空间分布非常不均匀。从图3所示的文献[12]超混沌式（1）所产生的相空间图来看，相图并非在单位平面[0，1）×[0，1）上呈均匀分布，表明该超混沌系统随机性相比图2所示的超混沌随机性明显差很远，因其相空间图存在稳定窗和大量空白区域，不利于用于图像加密产生高安全且高质量的密钥序列需要。

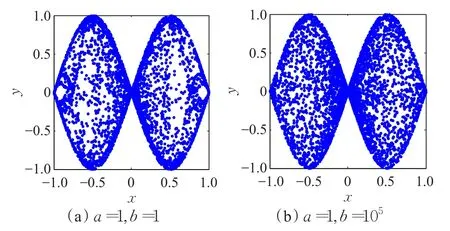
图3 文献[12]超混沌系统的相图

总之，通过对比图2、图3所示的两种超混沌系统相图分布均匀性程度，以及本文建议超混沌系统相比文献[12]超混沌系统能获得更加巨大的最大正李氏指数值，可判定本文建议超混沌系统式（2）具有一定的潜在优势[14-15]，通过超混沌序列获取系统参数和初始值更加艰难，有利于高安全场合信息加密和混沌通信等需要。

3 参数控制的同异或操作加密法

传统密码学中，一般采用密钥经异或操作（或者同或操作）对明文实现加密，解密时利用密钥经异或操作（或者同或操作）对密文解密并获得明文，这种加解密方法已在图像安全保护中得到广泛应用；但是，若选取加密的明文是0或255时，则可推算获取密钥信息，从而导致加密结果难以抵抗选择明文和差分等攻击，无法满足高安全性的军事、海监等场合的应用需要。为此，本文将探索参数控制的同或操作与异或操作相混合的加密方法。

假设密钥K和明文P均是L个字节的非负整数序列，对任意字节密钥ki和明文 pi进行异或操作或者同或操作可描述为：

或者

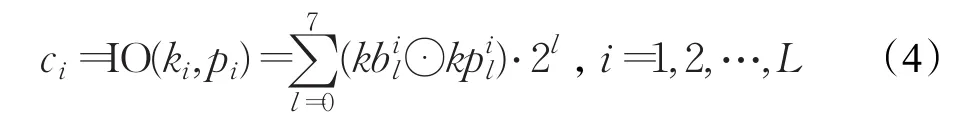
其中EO(ki,pi)和IO(ki,pi)分别表示字节整数ki和 pi之间的比特位异或操作和同或操作，ci,ki,pi∈{0,1,…,

面对同或操作与异或操作难以抵抗选取全为0或255的明文进行攻击分析的不足，本文提出参数控制的同或操作与异或操作相混合的字节整数之间的运算操作，定义描述如下：

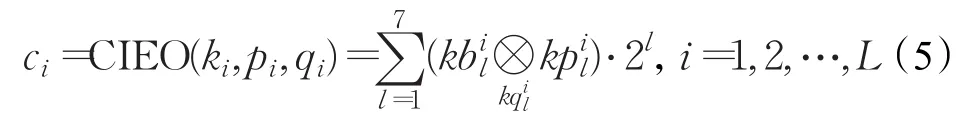
其中表示两个比特值之间的运算选择同或操作还是异或操作与参数取值密切相关。若参数等于1时，则选择异或操作；否则，选择同或操作。

参数控制的字节整数之间同或与异或相混合运算具有基本性质如下：

（1）若qi=255时，则混合运算CIEO(ki,pi,qi)退化为异或运算。

（2）若qi=0时，则混合运算CIEO(ki,pi,qi)退化为同或运算。

另外，同或运算与异或运算相混合操作式（5）仍满足ci=CIEO(ki,pi,qi)且 pi=CIEO(ki,ci,qi)的对偶性质，给图像加解密应用提供了理论基础。本文将上述同或与异或相混合运算式（5）用于改造现有的反馈结构加密机制[16]为：

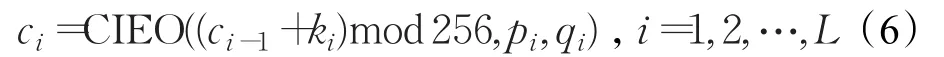
或者

也可将文献[17]增强型反馈加密结构修改为：

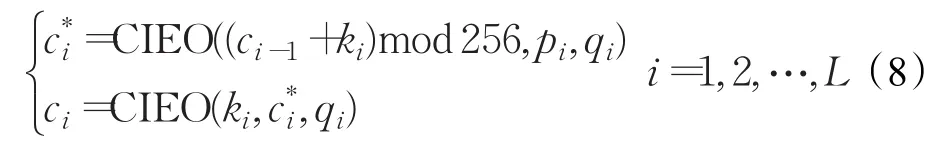
上述式（6）至式（8）的字节型非负整数序列qi和密钥序列ki可由本文建议高性能超混沌系统式（2）产生弱结构随机序列整数化获得。特别地，若随机序列qi取值全为255时，该种反馈结构加密法退化为文献[16-17]的加密机制。由于加密机制式（6）至式（8）中的参数序列qi可随机选取，相比文献[16-17]加密机制能明显提高抗选择明文攻击的能力。另外，这种改进的同异或操作可以推广至众多图像加密算法[18-19]，以便进一步提高它们的加密结果安全性。甚至，也可将这种参数控制的同异操作推广至DNA编码操作，以便增强文献[20]等DNA与混沌相结合的图像加密算法安全性。

4 图像加密算法设计

红外图像是通过测量物体向外辐射的热量而获得的，相比可见光图像相比具有分辨率差、对比度、信噪比低、视觉效果模糊、像素灰度值主要集中于中下灰度层次等特点。为保证红外成像系统中红外图像的安全，克服传统图像加密时方法安全性不高、实时性差等缺陷，本文提出了利用二维高性能正弦超混沌映射式（2）并结合参数控制同异或混合运算的反馈加密机制设计了一种新的图像加密算法，其框图如图4所示。由加密图像产生的图像特征信息与外部密钥相结合产生超混沌系统的参数和初始值，提高抗选择明文攻击能力。超混沌系统迭代产生像素值位置置乱的参数和像素正反向扩散操作的双密钥序列。图像加密包括像素位置置乱和像素值正反向扩散操作3部分组成，提高抗差分攻击能力。正反向扩散操作是双密钥序列驱动的异或与同或操作相混合的高安全加密机制[21]，它是保证加密安全的核心。

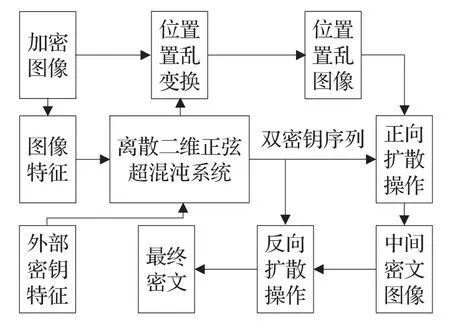
图4 图像加密框图

假设加密明文大小为M×N的灰度图像G=(gij)M×N，加密所得密文图像为G*=)M×N。加密过程描述如下：

步骤1选取长度为256个比特的外部密钥二进制序列且∈{0,1}(l=0,1,…,255)，将其转化为32个字节整数序列255}(l=0,1,…,31)。

步骤2计算明文图像G的均值和模特征量分别为：

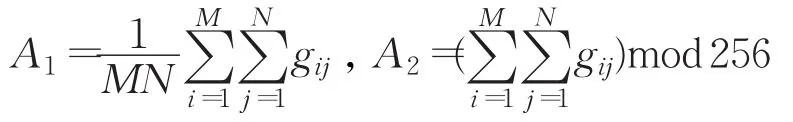
步骤3选取本文建议的8个二维正弦超混沌系统式的参数和初值分别为：

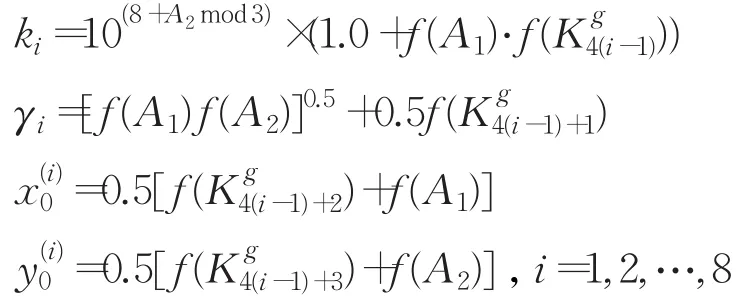
其中

步骤4对8个二维正弦超混沌系统分别迭代200次所得结果舍去，再迭代M×N次产生单位区间随机序列和(i=1,2,…,8;l=1,2,…,M×N)，将其处理为：

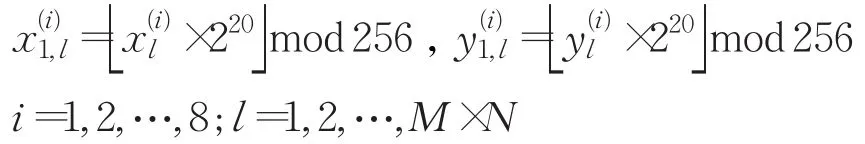
将和进行有限域乘法递归融合并产生：

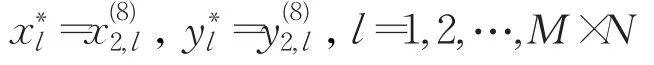
其中和定义为：

若i=1时，则=且=；否则，

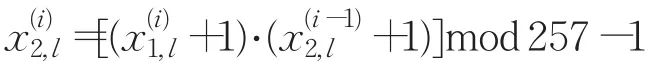
和

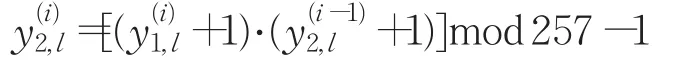
将序列和进行异或运算并获得密钥序列为=⊕，l=1,2,…,M×N。

步骤5对明文图像进行位置置乱10次，所采用的置乱方法为文献[22]改进不等长Arnold变换：

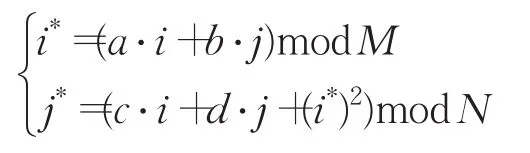
其中将置乱所得图像记为G'=()M×N。

步骤6将位置置乱后图像G'=()M×N转化为1维序列=且 l=(i-1)×N+j。

步骤7利用序列、和对序列按照式（8）进行正向扩散加密为：

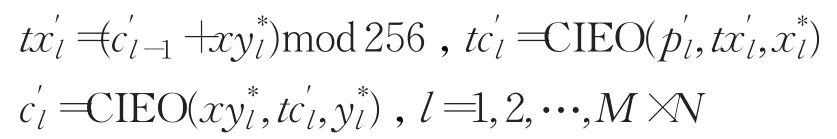
其中选取为A2。

步骤8对中间密文(l=1,2,…,M×N)按照式（8）进行反向扩散加密为：

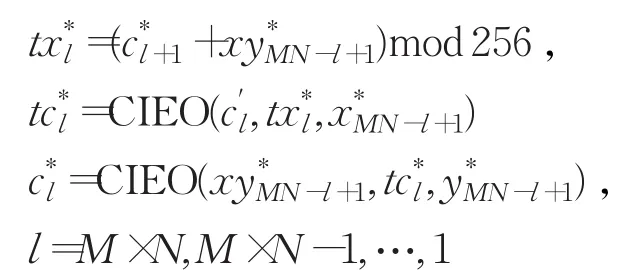
其中选取为255-A2。

步骤9将反向扩散加密结果(l=1,2,…,M×N)转化为矩阵，这里，i=1,2,…,M;j=1,2,…,N。

步骤10输出密文图像

5 密文图像伪装方法

面对传统图像加密结果是无意义的噪声图像，容易引起攻击者的怀疑，于是探索有意义的图像加密已成为新的发展趋势。文献[7-8]提出了利用小波变换产生有意义密文的加密算法，但不足是密文图像相比明文的大小有了显著增加（密文大小为明文图像大小的4倍），不利于网络传输和存储等需要。另外，文献[23]利用压缩感知理论提出无嵌入有意义加密法，密钥经耦合字典采用凸优化迭代学习非常耗时（算法复杂性非常高），不利于大幅面遥感影像伪装和实时性要求较高场合的应用需要。为此，本文提出一种快速的密文图像后处理方法，将密文图像变换成有一定意义的纹理图像；同时图像灰度直方图呈非均匀分布，给统计攻击带来更大的迷惑性。

万有引力定律是经典牛顿力学中的重要定律，文献[24]将其用于图像像素置乱并获得像素扩散操作方法，其本质是通过像素大小和位置坐标的远近产生像素扩散加密，即

其中k为引力系数且取较大的正值，m为单位质点的质量且取值为1，(x,y,z)是单位质点的空间坐标且z≠0，mij是图像(i,j)位置像素的质量，Bij是(i,j)位置像素灰度值，是像素置乱后灰度值。这种置乱扩散法仍促使密文图像呈无意义的杂乱噪声且灰度直方图呈均匀分布，难以获取原始图像的真实信息，但容易引起攻击者的怀疑。

在式（9）置乱扩散操作的启发下，本文提出一类新的变换法，利用像素位置信息对像素值进行修改，能将杂乱无章的密文图像伪装成一种有意义图像且灰度直方图呈非均匀分布。

假设密文图像G*=()M×N，经变换获得的伪装图像W=(wij)M×N，其变换伪装方法为：

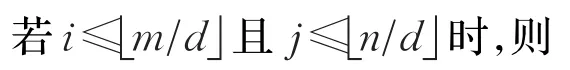
其中d为正整数且1,2,…,8)，常选取 d=2，rl=0.25(l=1,2,…,8)。

通过上述变换伪装所获有意义的纹理图像W=(wij)M×N，相应的灰度直方图呈非均匀分布，能增强统计攻击的迷惑性。本文建议的伪装密文图像方法的优势是仅需要扫描图像一遍就实现图像信息的伪装，相比文献[7-8，23]高复杂度的伪装方法，特别有利于实时性要求较高场合的图像信息保护需要。

6 仿真结果与分析

本文加密算法采用Matlab编程并在Matlab2013平台下进行系统测试。首先采用标准Lena等图像测试了加密算法的有效性，其次测试大小为220×210的低灰度级范围红外图像（图5（a）和图5（f）所示），限于篇幅有限而文中仅给出1幅图像的测试结果。该算法采用256比特的外部密钥，结合图像特征信息产生8个超混沌正弦映射的参数和初始值，8组超混沌映射产生像素值扩散操作的双密钥序列，控制同异或混合操作实现像素反馈扩散操作，加密结果经变换伪装成一定意义的纹理图像，其详细结果如图5（c）～图5（i）所示。

从上述图5所示的低灰度级范围红外图像的加密和伪装结果可见，本文建议的红外图像信息保护方法是非常有效的。

6.1 密钥空间

本文算法的外部密钥是256比特随机序列，并与图像特征信息相结合产生超混沌系统的参数和初始，加密算法的密钥空间大小为2256。密文经变换伪装获得有意义图像时，参数d为正整数且常取2、4至50，参数rl(l=1,2,…,8)常取范围为0.2至0.5。因此，本文加密算法的密钥空间明显超过文献[25]算法。另外，超混沌系统的参数和初始值不仅与外部密钥相关，而且也与图像特征信息相关，即使外部密钥相同，但加密图像不同，导致加密结果存在显著变化，能实现香农的一次一密密钥体制，有效抵抗穷举攻击。

6.2 密钥敏感性分析

图5 红外图像及加密伪装

敏感性是有效密码系统的基本特征，它包括两方面：一是使用不同的密钥对同一幅图像加密时，能产生两幅完全不同的加密图像；二是解密密钥发生稍微变化，也不能令加密图像得到正确解密。一般而言，常用图像像素变化率（Number of Pixels Change Rate，NPCR）和归一化像素值平均改变强度（Unified Average Changing Intensity，UACI）对加密算法的密钥敏感性分析，其定义如下：

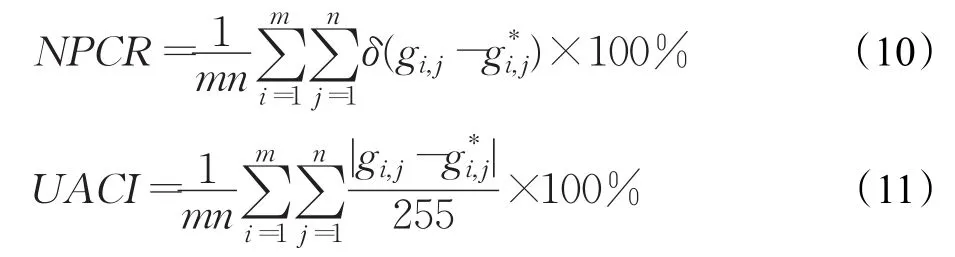
其中

针对图5所示的红外图像，256比特的外部密钥发生一个比特位变化，将密钥1变化为密钥2，所对应两幅密文如图6（b）和图6（c）所示，其相应差分图像如图6（d）所示，表明本文算法具有较强的密钥敏感性。另外，计算获得密钥稍微变化所对应加密图像的像素变化率NPCR为99.651 5%，归一化像素值平均改变强度UACI为33.561 2%，进一步证实本文算法对密钥变化具有极高的敏感性。

图6 不同密钥加密图及差分图像

若解密密钥与加密密钥稍有差异是无法正确解密获取明文图像的。限于篇幅有限，省略错误密钥所对应的解密结果。

6.3 抗差分攻击分析

抗差分攻击能力依赖于对明文图像的敏感度，对明文图像的敏感度越强，抗差分攻击能力越好。常用像素变化率NPCR和归一化像素值平均改变强度UACI两指标衡量算法的抗差分攻击能力。改变红外图像的任意像素值，测得算法的像素变化率NPCR为99.651 3%，归一化像素值平均改变强度UACI为33.561 4，表明本文算法具有较高的抗差分攻击能力，相比文献[16]算法（像素变化率NPCR为99.605 7%，归一化像素平均改变强度UACI为33.404 9%）也具有更强的敏感性。

6.4 信息熵分析

信息熵反映了信息的随机性和不可预测性。图像像素灰度值分布越均匀，信息熵越大，随机性越强，安全性越高。信息熵公式为：

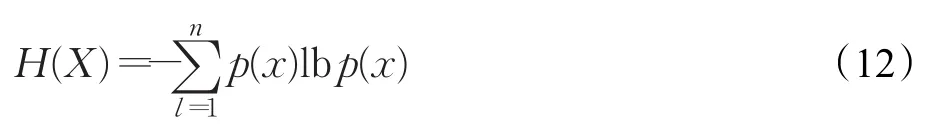
其中X是一个随机变量，文中为一幅灰度图像灰度级集合，p(x)表示图像灰度级x出现的频次率，n为灰度级数。通常，灰度图像为256个灰度级，其理想信息熵值为8（均匀分布）。本文算法所对应扩散加密密文的信息熵为7.996 4，它与理想信息熵值非常接近，表明本文像素扩散加密法的随机性好，不确定性高，安全性好。另外，文献[26]提出了直方图方差法度量直方图分布的均匀性程度，其本质是直方图偏差，它与信息能量度量直方图均匀性是等价的。由于信息能量与信息熵之间呈对偶关系[27]，本文不再利用直方图方差法评价图像加密结果所对应的直方图分布均匀性程度。

6.5 相关性分析

一幅图像相邻像素值较为相似，则相关性较高。图像经像素位置置乱和像素值扩散操作之后，相邻像素值毫无规律，其相关性较低。计算相邻像素相关性公式为：

其中

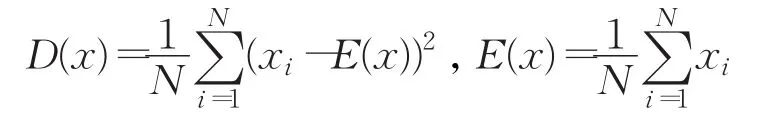
上述式（13）中x,y表示图像相邻像素的灰度值，r(x,y)表示相邻像素的相关系数，N表示相邻像素对的数目。随机选取图5所示的红外图像、置乱和扩散操作所获密文图像中相邻3 000个像素对进行测试，所得结果如图7和表1所示。

从图7所示相邻像素分布图可看出，明文图像相关性较高，分布于斜率为1的直线附近。密文图像在矩形区域内呈均匀分布。从表1所示的相邻像素相关系数可看出，加密前明文像素具有较高的相关性；而加密后密文像素具有非常弱的相关性，表明本文算法对于降低相邻像素相关性取得的效果相比文献[25]更好。

6.6 密文像素空间分布

纹理图像常借助相邻像素共生矩阵进行特征提取分析。本文将相邻像素共生直方图熵作为度量图像加密像素空间分布均匀性指标。对红外图像进行置乱和扩散操作所得密文的水平和垂直方向相邻像素的共生直方图如图8所示。不同方向相邻像素的共生直方图均匀性程度可采用信息熵描述，其定义为：

图7 相邻像素分布图

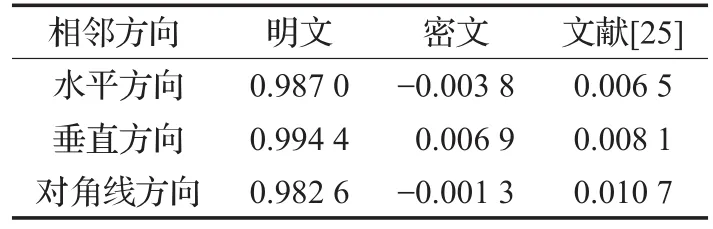
表1 相邻像素的相关系数

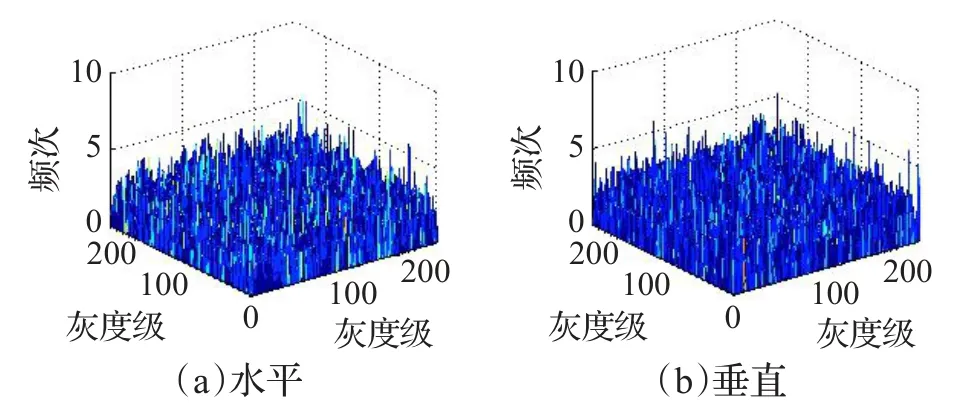
图8 相邻像素共生直方图

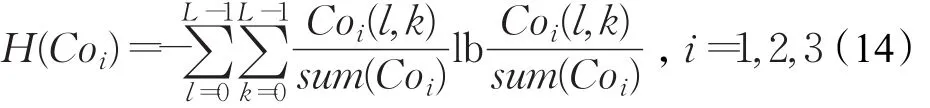
其中

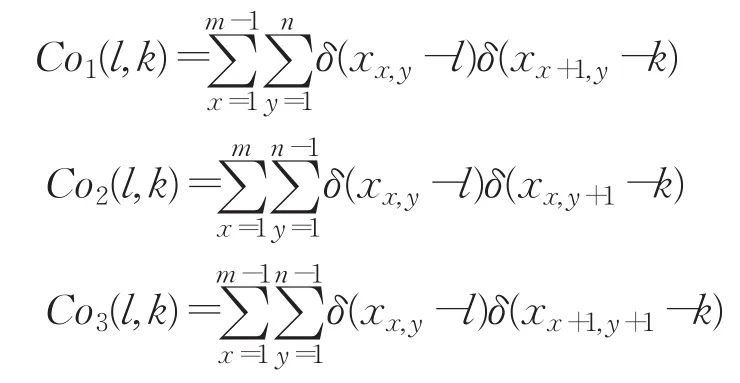
l,k=0,1,…,255

若像素空间分布呈理想均匀分布时，其不同方向相邻像素对出现的概率应为1/2562，相应信息熵达到最大为16.0。通过测试获得红外明文图像水平、垂直和对角线3方向相邻像素对所对应共生直方图信息熵分别为4.623 3、4.291 7和4.705 4，表明红外明文图像像素空间分布极不均匀。然而，通过本文加密算法所获密文水平、垂直和对角线3个方向相邻像素对所对应共生直方图信息熵分别为14.872 3、14.875 2和14.874 3，它们与理想共生矩阵信息熵16相差并不大，表明本文加密方法能促使密文像素空间分布非常均匀。

6.7 像素扩散操作安全性分析

图像加密主要包括像素位置置乱和像素值扩散操作两方面，其中大多数加密算法的像素位置置乱和像素值扩散操作相互独立，采用传统异或与有限域加法操作相结合的加密算法无法抵抗选择特殊明文如灰度值全为0或255的单灰度级图像进行攻击，根本原因在于像素位置置乱对于取值为某一灰度级的单值图像是无效的，导致扩散操作攻击分析容易获取像素扩散操作的密钥，从而对密文进行破解并获得明文图像。如文献[25]加密算法，其位置置乱和扩散操作相互独立，像素扩散操作采用c1(l)=c1(l-1)⊕k(l)⊕p(l)进行正向扫描加密产生中间密文c1(l)(l=1,2,…,mn)，再采用反向扫描c2(l)=c2(l+1)⊕k(l)⊕c1(l)加密产生最终密文 c2(l)(1≤l≤mn)。若选取特殊明文 p(l)=0(1≤l≤mn)时，则加密所得密文c2(l)(1≤l≤mn)。假设c2(mn+1)已知时，利用k(l)⊕c1(l)=c2(l)⊕c2(l+1)，可获得 k(l)⊕c1(l)(1≤l≤mn)。又因明文p(l)=0(1≤l≤mn)，可将正向扫描加密 c1(l)=c1(l-1)⊕k(l)⊕p(l)简化并获得c1(l)=c1(l+1)⊕k(l+1)。再利用反向扫描加密所对应的k(l)⊕c1(l)=c2(l)⊕c2(l+1)，在已知c2(mn+1)条件下可推断得到c1(l)(0≤l≤mn-1)。进一步，再利用 p(l)=0(1≤l≤mn)和 c1(l)=c1(l-1)⊕k(l)，可得 k(l)=c1(l)⊕c1(l-1)(1≤l≤mn-1)。但是，k(mn)是无法推断获得，它仅有256个穷举值。因此，在穷举c2(mn+1)和k(mn)共计62 256次时，能完全获取该加密算法的密钥，这表明该算法存在一定安全隐患，不适合高安全级别的图像加密需要。

本文加密算法引入参数控制的异或与同或相混合的扩散机制，其本质是双密钥扩散加密法，一个密钥控制异或与同或操作的选取，另一密钥参与密文的产生。该种扩散操作不仅具有良好的非线性扩散能力，而且双密钥产生由本文建议的具有较大正李氏指数超混沌产生，仅利用特殊明文加密所对应的密文无法破解获取双密钥，从而间接保证该加密算法具有良好的抗选择明文等攻击能力，其详细分析过程如下。

针对本文加密所采用的加密机制为：

若选取pi=0(i=1,2,…,L)，已获得密文为ci(i=1,2,…,L)，于是利用加密表达式ci=CIEO(ki,,qi)因参数ki和qi未知而无法获得。此时，假设穷举搜索已知ki和qi，利用ci=CIEO(ki,,qi)可获得，再利用加密表达式=CIEO((ci-1+ki)mod256,0,qi)，根据已知的和qi，可获得一个新的ki计算值，若它与穷举值ki不一致，再对ki和qi穷举直至获得的ki计算值和穷举值相同，此时获得加密密钥ki和qi，其穷举次数为256×256。于是，按照这种思路获取图像加密密钥序列ki,qi(i=1,2,…,L)的穷举次数为(256×256)L，其统计攻击分析时间复杂性为O(2562L)。针对大小为256×256的密文图像，穷举攻击次数达到62 25662256次数，才能获取完整的双密钥序列。因此，本文所建议的加密机制相比文献[25]方法抗选择明文攻击的安全性有了显著改善。另外，文献[28]指出一个加密系统若能抵抗选择明文攻击，就能抵抗选择密文、明文和密文等攻击，限于篇幅有限不再讨论。

6.8 明文与伪装图的差异性分析

将明文图像加密成杂乱无章且类似噪声的密文图像，可达到保密图像的目的；但是，这种密文图像容易引起攻击者怀疑，采用选择明文、密文进行攻击分析并获取密钥，从而导致加密结果安全性差。本文将加密获得的密文伪装成有一定意义的图像，可降低攻击者的怀疑程度，间接提高加密图像的安全性。因传统PSNR指标无法真实刻画两图像像素差异性程度，下面采用分块平均变化强度[29]（Block Average Changing Intensity，BACI）度量明文与伪装图之间的差异性，其定义为：

该分块平均变化强度值能刻画两幅大小相同的灰度信息差异程度。该值越大，则表明两幅图像相似程度越低。针对图5所示的红外明文图像与其加密伪装图像之间BACI值如表2所示。

表2 明文与密文伪装图之间的BACI值

另外，给定参数rl(l=1,2,…,8)，参数d从2至50变化，测得明文与伪装图之间的BACI值变化不明显，表明参数rl(l=1,2,…,8)对伪装图变化影响较大。通过测试该明文与随机图之间BACI值均大于20.381 1，表明本文所建议的明文与伪装图之间的差异性是非常显著而有意义的。

总之，为了提高图像加密的安全性，国内外众多学者提出了不同类型混沌系统并将其应用于图像加密[30-34]；但是，无论是低维还是高维混沌系统的构造都希望混沌系统随参数变化鲁棒性强且对初始值和参数变化极为敏感（即最大正李氏指数值越大越好），所产生的密钥序列越接近真实随机序列，更有利于加密系统安全性提高的需要，这将成为混沌系统及其加密应用中永恒不变的追求。

7 结束语

本文利用正弦函数与反馈调制机制相结合构造了二维正弦函数超混沌系统，适当选取参数获得该系统的最大正李氏指数超过20.0。该系统产生的弱结构拟真随机序列控制异或运算与同或运算相混合的反馈扩散加密法，实现图像高安全性加密。将密文经灰度变换伪装成有意义的图像，降低了密文攻击者的怀疑，有利于信息安全保护的需要。

另外，本文提出的密文伪装方法存在的不足是伪装图像较为简单，图像信息丰富性和多样性欠少。接下来，将引入分形动力学产生分形几何图形的思想，利用密文信息驱动分形动力系统参数，继续探索新的密文图像伪装方法，以便产生更多实际意义的伪装图像。

参考文献：

[1]Harram I M，Bakura M U M，Mohammed A M，et al.Recent trends in image encryption：A review[J].Journal of Information Sciences and Computing Technologies，2016，5（3）：519-528.

[2]赵锋，吴成茂.自编码和超混沌映射相结合的图像加密算法[J].计算机辅助设计与图形学学报，2016，28（1）：119-128.

[3]陈滨.混沌波形的相关性[M].西安：西安电子科技大学出版社，2011：77-87.

[4]朱和贵.信息安全中混沌图像加密算法及其相关问题研究[D].长春：吉林大学，2014.

[5]魏娜.混沌同步和加密中若干问题的研究[D].辽宁大连：大连理工大学，2015.

[6]刘杨.混沌伪随机序列算法及图像加密技术实现[D].哈尔滨：哈尔滨工业大学，2015.

[7]Bao L，Zhou Y C.Image encryption：Generating visually meaningful encrypted images[J].Information Sciences，2015，324（10）：197-207.

[8]Kanso A，Ghebleh M.An algorithm for encryption of secret images into meaningful images[J].Optics and Lasers in Engineering，2017，90（3）：196-208.

[9]陈志刚，梁涤青，邓小鸿，等.Logistic混沌映射性能分析与改进[J].电子与信息学，2016，38（6）：1547-1551.

[10]Wu Y，Yang G L，Jin H X，et al.Image encryption using the two-dimensional logistic chaotic map[J].Journal of Electronics Imaging，2012，21.

[11]Hua Z Y，Zhou Y C.Image encryption using 2D Logisticadjusted-Sine map[J].Information Sciences，2016，339：237-253.

[12]Liu W H，Sun K H，Zhu C X.A fast image encryption algorithm based on chaotic map[J].Optics and Lasers in Engineering，2016，84：26-36.

[13]Ramadan N，Ahmed H E H，Elkhamy S E，et al.Chaosbased image encryption using an improved quadratic chaotic map[J].American Journal of Signal Processing，2016，6（1）：1-13.

[14]Elhadj1 Z，Sprott J C.On the robustness of chaos in dynamical systems：Theories and applications[J].Frontiers of Physics in China，2008，3（2）：195-204.

[15]Hua Z Y，Zhou B H，ZHou Y C.Sine-transform-based chaotic system with FPGA implementation[J].IEEE Trans on Industrial Electronics，2018，65（3）：2557-2566.

[16]朱从旭，胡玉平，孙克辉.基于超混沌系统和密文交错扩散的图像加密新算法[J].电子与信息学报，2012，34（7）：1735-1743.

[17]刘红，肖云鹏，徐光侠.双向扩散的图像加密算法安全性分析和增强[J].数字通信，2014，41（3）：34-37.

[18]Wang X Y，Yang L，Liu R，et al.A chaotic image encryption algorithm based on perceptron mode[J].Nonlinear Dynamics，2010，62（3）：615-621.

[19]Zhang H，Wang X Y，Wang S W，et al.Application of coupled map lattice with parameter q in image encryption[J].Optics and Lasers in Engineering，2018，88：65-74.

[20]Liu H Y，Wang X Y，Kadir A.Image encryption using DNA complementary rule and chaotic maps[J].Applied Soft Computing，2012，12（5）：1457-1466.

[21]朱从旭，孙克辉.对一类超混沌图像加密算法的密码分析与改进[J].物理学报，2012，61（12）.

[22]吴成茂.二维不等长变换的改进及其应用[J].计算机辅助设计与图形学学报，2015，27（8）：1529-1538.

[23]韦星星.基于结构化信息的图像内容分析与理解[D].天津：天津大学，2015：41-55.

[24]孙玉辉，陈建华.一种基于万有引力模型的图像置乱方法[J].福建师范大学学报：自然科学版，2006，34（1）：47-50.

[25]林青，张延江，王珺.基于超混沌系统的图像加密算法[J].中国科学：技术科学，2016，46（9）：910-918.

[26]Zhang Y Q，Wang X Y.A new image encryption algorithm based on non-adjacent coupled map lattices[J].Applied Soft Computing，2015，26：10-20.

[27]Amari S，Nagaoka H.Methods of information geometry[M].Oxford：Oxford University Press，2000.

[28]Wang X Y，Teng L，Qin X.A novel colour image encryption algorithm based on chaos[J].Signal Processing，2012，92（4）：1101-1108.

[29]张勇.混沌数字图像加密[M].北京：清华大学出版社，2016：87-92.

[30]Yuan H M，Liu Y，Lin T，et al.A new parallel image cryptosystem based on 5D hyper-chaotic system[J].Signal Processing：Image Communication，2017，52：87-96.

[31]冯泽仲，王晓东.基于忆容器混沌电路设计及图像加密算法[J].计算机与应用化学，2017，34（3）：251-256.

[32]Radwan A G，Abdelhaleem S H，Abd-El-Hafiz S K.Symmetric encryption algorithms using chaotic and nonchaotic generators：A review[J].Journal of Advanced Research，2016，7：193-208.

[33]He J B，Yu S M，Cai J P.Analysis an design of anticontrolled higher-dimensional hyperchaotic system via lyapunov-exponent generating algorithms[J].Journal of Applied Analysis and Computation，2016，6（4）：1135-1151.

[34]Chai X L，Gan Z H，Yang K，et al.An image encryption algorithm based on the memristive hyperchaotic system，cellular automata and DNA sequence operations[J].Signal Processing：Image Communication，2017，52：6-19.