随机需求有时间窗的路径优化及补救策略研究

邓 烨，朱万红，唐 建

DENG Ye,ZHU Wanhong,TANG Jian

解放军理工大学 野战工程学院，南京 210001

College of Field Engineering,PLAUniversity of Science and Technology,Nanjing 210001,China

1 引言

现代城市物流配送中存在很多需求不确定的情况，例如运钞车对银行网点进行存取款服务，应急中心对灾害点进行应急配送等，这些都是要求在需求信息不充分的情况下完成物流配送任务。如何在保证服务质量的前提下尽量降低配送成本，是物流配送者最为关心的内容，因此随机需求的车辆路径问题（Vehicle Routing Problem with Stochastic Demand，VRPSD）研究得到广泛关注[1]。传统VRPSD问题一般不考虑客户的时间窗约束，而在现实中，是否满足时间窗约束往往也是评价服务质量的重要标准之一，因此需要加以考虑[2]。同时，针对需求超出容量约束时的传统补救策略由于偏于保守，往往造成违反客户时间窗的风险成本较高，因此需要提出更加敏捷可靠的补救策略。

目前，关于随机需求车辆路径问题一般是基于先验序列的两阶段优化方法[3]，而先验序列的确定一般是基于机会约束规划（Chance Constrant Programming，CCP）和二元可能性理论进行研究[4]。基本的机会约束规划模型以预设成功服务概率作为约束，不考虑服务失败情形下的风险成本，适用于需求服从连续分布情况，可通过确定等价式转化为确定性模型求解。基本二元可能性理论只考虑需求是二元、离散情况[5]，根据服务的期望成本范围以及服务失败情形下的风险成本来确定先验路线。考虑到真实客户需求量具有多种可能性，并非简单二元结构，因此本文采用机会约束规划理论求解先验路线，并采用预优化策略[3]进行补救调整，即根据服务失败情况下的总服务成本确定最优的服务概率和计划配送路线，然后再对不满足实际需求的客户进行补救。

针对服务失败（容量超出）的情况，一般按照Teodorović提出的补救策略对客户进行补救[6-8]，其中Yee[9]针对计划路线配送失败情况下的动态调度策略进行了研究。在现实中，由于不同配送中心的信息化服务水平不同，导致应对服务失败情况的补救策略有很大差异。在信息化水平较低的配送中，车辆发现服务失败一般是返回中心重新装载；当信息化水平较高时，一旦发现超出容量范围则可以即时通知中心重新派出新车；而当信息化水平最高时，可以通过一定的预测提前判断容量是否超出并且即时通知中心派出新车。不同补救策略下的风险成本是明显不同的，因此，研究不同信息化水平的补救策略如何影响风险成本对决策者而言具有重要的指导意义。

2 问题描述及数学模型

2.1 问题假设及目标

本文研究的是现代城市物流配送中的随机需求且有时间窗的车辆路径优化问题，目前仅有较少文献对含有时间窗约束的随机车辆问题进行研究[2，10-11]，为了不失一般性，综合以上文献中的基本假设内容，对本文研究问题进行如下假设：（1）客户需求量是连续随机变量，服从连续概率分布且不小于0；（2）客户具有服务时间窗，只有在时间窗口内才可以进行服务，提前到达的车辆需等待到开始时刻再进行服务，超出截止时刻到达的车辆则认为配送失败，因此具有严格的时间窗约束，但若由于不满足随机需求量进行补救而超出时间窗的，则仅需对超出时间窗的部分给予惩罚；（3）每个客户原则上只被服务一次，除非由于不满足需求量而进行补救；（4）车辆行驶速度假设为定值1，且路段间的行驶速度恒定不变，车辆的车型相同，车容量相同，不考虑车辆最大行驶距离或最大行驶时间约束；（5）每辆车服务完所有客户后返回配送点，同时每辆车在完成其所有计划客户后才支付单辆车的报酬（多次发车补救也只算为单辆车）。

在这里，假设客户需求为非负的连续随机变量具有一般性，从长远时间来看，离散随机变量可以看为连续，而需求为0的随机变量代表该客户不需要服务；同时假设时间窗约束在预优化阶段为严格约束，在补救阶段则被松弛（否则均为不可行解），体现了含有时间窗的随机需求模型的特殊性。只有在这些假设基础上，才能进行模型的构建和求解。

基于以上假设，问题的优化目标是在满足客户容量约束和时间窗约束的条件下使总服务成本最少，达到经济效益的最大化。这里的总服务成本是指各车的派出成本与行驶成本之和，即在最小化派出的车辆数的前提下尽量缩短服务距离。

2.2 符号说明

随机需求有时间窗的车辆路径问题（Vehicle Routing Problem with Stochastic Demand and Time Windows，VRPSDTW）是基本VRPTW模型的一种衍生模型。因此，可以在Desrochers等[12]提出的传统网络流公式体系下进行描述。

设G=(V,D)是一个完全有向图，V={v0,v1,…,vn+1}代表所有点的集合，其中v0和vn+1代表1个配送中心点和1个虚拟配送中心点，其他点代表客户，构成客户点集C={v1,v2,…,vn}；每个客户点存在一个随机需求qi≥0，并且假设其服从某一概率分布Ui，还存在服务时间si≥0，并且要求在时间窗[ei,li]内得到服务，配送中心的服务时间窗口为[0,Tmax]；任意两点组合构成一条边，则 D={(vi,vj)|(vi,vj)∨(v0,vi)∨(vi,vn+1),vi,vj∈C,i≠j}代表道路边集，每一条边(vi,vj)∈D都有一个权重，即距离dij且dij≥0；任一车辆k∈K ，每辆车的最大载重量为Q。

2.3 数学模型

为了对VRPSDTW问题进行建模，首先需要定义两个决策变量：

（1）二进制决策变量：

（2）非负实数决策变量：车辆k服务完客户vi（包括配送中心）后的出发时间。

最终，可以构建VRPSDTW为一个机会约束混合整数规划数学模型。

目标函数：

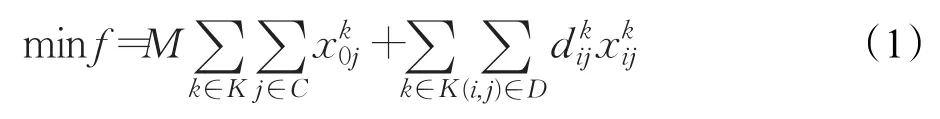
约束条件：

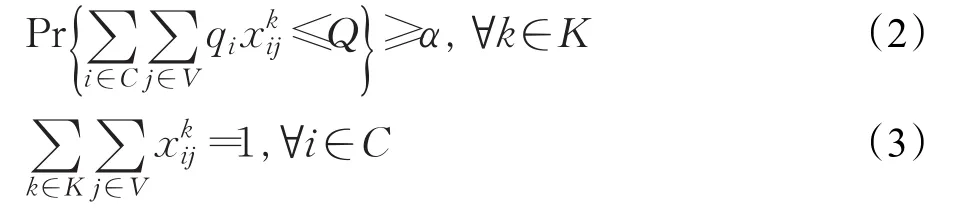
其中，式（1）表示最小化总的配送成本，默认单辆车的派出成本远大于单位距离成本，M设置为一个较大的常数；式（2）表示随机容量约束，Pr为概率测度，α为设定的满足容量约束的最低概率值α∈(0,1]，qi为客户i的随机需求量；式（3）表示每个客户必须并且只能被访问一次；式（4）表示任何到达某一客户的车必须还从同一个客户处离开；式（5）表示每辆车必须从配送中心出发最后还必须返回中心；式（6）表示每辆车离开中心最多一次，同时其返回中心也最多一次；式（7）表示对某点的服务开始时间必须介于该点的时间窗内；式（8）表示车辆从上一点出发到达下一点的到达时间一定不晚于下一点的服务开始时间。

2.4 模型转化与分析

2.4.1 随机约束转化

由于本文考虑的模型含有随机需求，是一类随机约束优化模型，一般方法是通过随机模拟需求进行仿真。该方法具有不受分布类型限制，适用性强的优点，但也存在很大缺陷：（1）仿真次数要求高，计算量很大。尤其是当问题规模也很大的时候，随机模拟的计算时间会非常长；（2）计算结果不稳定，即使经过大量的仿真，也不能保证得到理论最优解。因此，本文假设需求变量服从独立正态分布，这样就可以基于不确定原理[13]，将机会约束式（2）转化为确定等价形式进行求解，见式（9）。

其中，Φi(q)为正态分布N(μi,σi)的分布函数，(α)为分布函数的反函数，即求α分位点处的q值。

这样转化以后，实际是将随机约束规划模型转化成了一般的确定性约束规划模型，大大降低了计算量，同时可以保证得到理论上的最优解。这里，考虑到真实情况的复杂性，某段时期内客户的需求量当然不可能完全符合正态分布，但是根据中长期统计的客观数据，以及中心极限定理，可认为需求变量服从独立正态分布并不失其一般性。

2.4.2 补救策略分析

模型在随机约束条件或其确定等价式下算出的最优解只能作为计划配送方案，而现实中一旦部分客户的需求量太大，使得计划配送方案中剩余部分客户的需求无法满足，则需要额外进行配送补救。而补救策略的不同，额外增加的成本和时间也不同。本文基于不同的物流信息化水平，给出3种补救调整策略分别为：

（1）策略1：某辆车按照计划路线配送，若在到达客户i时得知其需求超出当前剩余货量，则卸载全部货量后返回中心重新装载货物，然后立刻返回客户i补充剩余需求，并继续按照原计划配送路线服务后续客户；若在服务完客户i后剩余货量正好为0，而后面还有客户，则立刻返回中心重新装载，然后直接开始服务后续客户。

（2）策略2：某辆车按照计划路线配送，若在到达客户i时得知其需求超出当前剩余货量，则立刻通知中心即刻派出新车服务客户i及其后续客户，原车卸载全部货量后返回中心；若到达客户i时发现服务完后的剩余容量将正好为0，而后面还有客户，则立刻通知中心即刻派出新车服务后续客户，原车服务完客户i后直接返回中心。

（3）策略3：某辆车按照计划路线配送，若在到达客户i时发现在满足其需求后剩下的载货量不足以满足下一个客户的计划需求量，则立刻通知中心派出新车开始服务后续客户，原车服务完客户i之后，直接返回中心；若在到达客户i时发现当前的需求已无法满足，则立刻通知中心派出新车到客户i补充剩余需求，然后按照计划路线服务后续客户，原车卸载全部货量后返回中心。

以上策略均假设到达客户即可知道当前准确需求量，同时配送中心已经准备好额外用车，不需增加额外装货时间。其中第一种策略是目前被所有相关文献采用的补救策略，其后两种是本文所提出的信息化补救策略。直观上看，第一种策略信息化水平最低，偏向于保守与经济，即使发现容量不满足，车辆也要等服务完毕才返回，并且不增加额外车辆，仅增加额外车次；第二种策略信息化水平一般，偏向主动与高效，一旦发现不满足需求，即刻通知中心派出新车；第三种策略信息化水平最高，最为高效，通过预测下一点无法服务，在还未服务下一点时就通知中心派车，因此能最大程度保证服务的成功性，但同时以损失一定经济效益为代价，可能会造成车辆和货物的浪费。这三种策略将在第4章中给出仿真比较。

3 算法设计

3.1 混合进化算法

带有时间窗车辆路径问题（VRPTW）是一类组合优化问题，可行解的数量会随着问题的规模呈指数增长，是典型的NP-hard问题[14]，本文研究的VRPSDTW问题同样如此，当问题规模较大时，传统的精确算法在有限时间内已不可能求解，必须设计智能算法进行求解。为了提高算法效率，本文设计了包括最近邻初始化算法、Falkenauer交叉算子、多样化变异算子和改进选择策略的混合进化算法（Hybrid Evolution Algorithm，HEA），以求实现算法收敛速度和收敛精度的平衡。混合进化算法流程见图1。

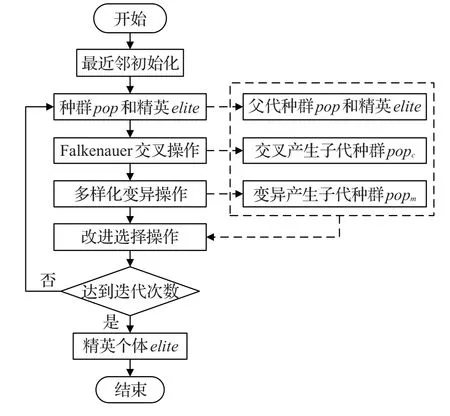
图1 混合进化算法流程图

3.2 编码与最近邻初始化

路径优化这一类组合优化问题一般采用随机排列访问点的实数编码方法构造解。如图2所示，0代表配送点，其他为客户点，每个0后面代表一条配送路线，有多少0，就代表有几条配送路线。

图2 染色体编码案例

然而，由于产生可行解本身就是一个NP-hard问题，采用随机初始化的方法很难在有限时间内得到足够数量的种群。因此，参考Solomon[15]的初始化方法，提出一种随机参数最近邻启发式算法初始化种群。首先，需重新定义任意两点间的距离d′ij：

式中，dij代表行驶时间（速度为1）；Tij代表下一点开始服务时刻与上一点出发时刻的差，Tij=bj-(bi+si)，bj=max{ej,bi+si+dij}；Vij代表下一点到达时刻与下一点服务结束时刻的差，Vij=lj-(bi+si+dij)；δi为随机归一化系数，且。随机初始化算法首先随机生成与种群个数相同的多组系数δi。

算法从配送中心点开始，每次选择d′ij值最小的点作为下一个访问点，当不满足约束条件时，返回配送中心，重新派出车辆开始选剩下的点直到所有客户均被访问完毕，重复此过程直到生成所有初始种群。

3.3 Falkenauer交叉算子

交叉算子采用Falkenauer[16]提出的经典形式。首先从第一个父代中选择随机数量的子路径给子代，然后从第二个父代中选择不含有当前子代客户点的子路径给子代，如果还有客户未被选中，则按照剩余点在第二个父代中的顺序依次尝试插入新路径中，如果无法插入，则新建一条子路径。如图3所示，交叉产生的子代均为可行解，将其放入子代种群popc中。

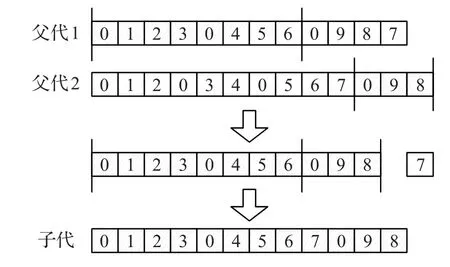
图3 Falkenauer交叉算子示意图

3.4 多样化变异算子

传统进化算法一般只采用一种变异策略，导致解的邻域结构比较单一，解的搜索空间狭窄，而采用多样化变异策略可以显著弥补这些缺陷。本算法中采用六种变异算子来对种群进行变异操作，分别为“交换（Exchange）”、“移动（Relocate）”、“组合（Combine）”、“分解（Split）”、“转换（Shift）”和“反转（Converse）”。如图4所示，白色方块代表真实配送中心，灰色方块代表虚拟配送中心。算法依次选择种群样本个体，按照变异概率进行变异，每次变异开始后，随机选择一种变异方式执行，如果变异成功生成可行解，放入子代种群popm中。

3.5 改进选择策略

传统的选择策略多是直接对子代进行选择，误差较大，较优解易丢失。因此，这里将全局最优解、父代种群和子代种群进行混合，一起参与下一次的选择。另外，传统基于适应值进行概率赋值的选择方法在进化早期易陷入“早熟”，后期由于适应值差异不大易造成收敛速度变慢，而基于适应值的排序数进行转化的赋值方法不随适应值大小而变化，只由当前序值决定被选概率，因此可以避免局部收敛，提高收敛速度[17]。在此基础上，本文提出基于Boltzmann序值的概率赋值方法。在机器学习和自适应控制等领域，Boltzmann选择策略（Boltzmann selection policy）被搜索算法所广泛采用，它模拟了自然界中温度的非线性下降过程，因此也是模拟退火算法的核心思想。

首先，按照函数目标值由小到大排序（目标值越小则越优）；然后，按照式（11）、式（12）对每个序数对应的个体赋给概率值：

式中，Pi代表排在第i位的个体在轮盘赌中被选择的概率；n为参与选择的染色体个数；T为当前温度，T0为初始温度，默认T0=100，iter为当前迭代次数。

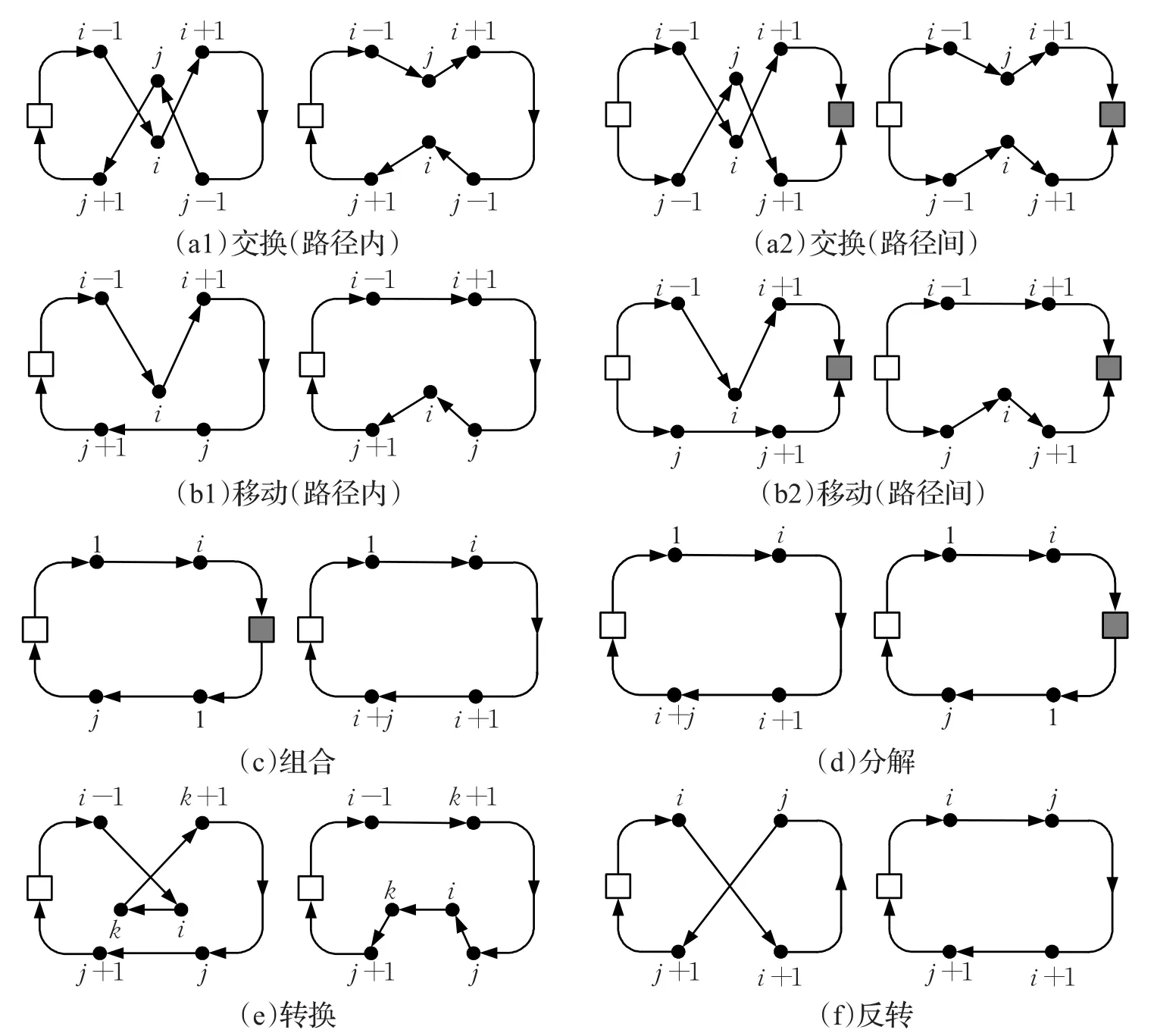
图4 六种变异算子示意图

最后，按照概率值Pi进行轮盘赌，有放回地选出与父代种群相等数量的子代种群pop，作为下一次交叉和变异的种群，同时记录最佳个体，将其与全局最佳比较，如果更优，则更新全局最优解。

3.6 约束处理方法

一般约束处理方法有以下几种[18]：惩罚函数法、修复法、分离目标和约束法等。在本算法中，采用分离目标和约束法，因为该方法避开了惩罚系数难以选择的困难，是一种更为有效且通用的约束处理机制[19]。

在预优化阶段，算法执行严格的约束条件，即只接受可行解，变异和交叉操作只产生可行解，不可行解直接舍弃，因此每次产生的子代种群数是不同的，有时候甚至找不到可行解。但由于本算法中交叉算子每次交叉只产生可行解，同时多样化变异算子具有较强的变异能力，因此并不会出现找不到可行解或可行解都相同的情况。

算法需要处理两类约束：车辆容量约束和客户时间窗约束。对于车辆容量约束，按照式（9）判断，根据设定的成功服务概率α可以求得每个解sol的任一子路径r′的总计划需求量，若有，则解sol满足容量约束。对于客户时间窗约束，需要判断到达时间是否在当前客户截止服务时刻之前。因此，若有Ati≤li,∀i∈r′,r′∈sol，则解 sol满足时间窗约束，其中，

4 实验与分析

所有实验和算法基于Matlab R2016a软件平台进行，算法参数设置如下：种群数 popsize=100，交叉概率ρc=0.5，变异概率ρm=0.5。考虑城市物流配送一般需要服务的客户数量相对较多且问题复杂性也易随客户数量变化而改变，为了不失一般性，本文以Solomon的VRPTW标准问题集为例，将其转化为具有随机需求问题的测试集进行实验。基本测试集可在以下网站下载：http：//w.cba.neu.edu/～msolomon/problems.htm，鉴于篇幅限制，这里仅选择RC108数据为例进行实验。基本算例RC108中有100个客户，客户呈随机和聚集混合形式分布，车辆载重Q=200。模型按照式（1）计算函数适应值，其中M=1 000。

4.1 基于确定需求模型的算法改进实验

本文采用的混合进化算法主要在两方面进行了改进：多样化变异策略和选择策略。这两项策略分别通过扩大搜索空间和增加种群多样性，防止算法陷入局部收敛。为了验证算法改进的有效性，设计了两组对比实验进行说明，一组用于比较变异操作的改进效果，一组用于比较选择操作的改进效果。暂时只考虑确定需求情况，通过分析基本VRPTW模型求解结果，验证算法的有效性。

4.1.1 变异操作对比

在本文混合进化算法基础上，分别设置单种变异算子和随机多样化变异算子进行对照，设置迭代数IterMax=200，最优适应值对应的路径总长度收敛结果见图5。

图5 变异算子改进结果对比图

可见，单独采用一种算子的收敛效果远没有综合采用六种算子的效果好，通过不同算子的组合，可以搜索到单个变异算子不可能搜索到的邻域解，使发现较优解的概率大大提高。

4.1.2 选择策略对比

在采用多样化变异算子的基础上，分别比较基于适应值的随机通用采样（Stochastic Universal Sampling）[20]、基于指数序值的轮盘赌和基于本文提出的Boltzmann序值的轮盘赌三种选择算子，设置迭代数IterMax=1 000，结果见图6。

图6 选择算子改进结果对比图

可见，Boltzmann序值算子很好结合了随机通用采样算子和指数序值算子的优势，在前期收敛较快，在后期也有较强的寻优性能。

同时，在采用Boltzmann序值轮盘赌算子的基础上，对三种不同保留策略的收敛情况进行比较，分别为：（a）子代、精英解混合选择策略；（b）子代、父代混合选择策略；（c）子代、父代和精英解混合策略，结果见图7。

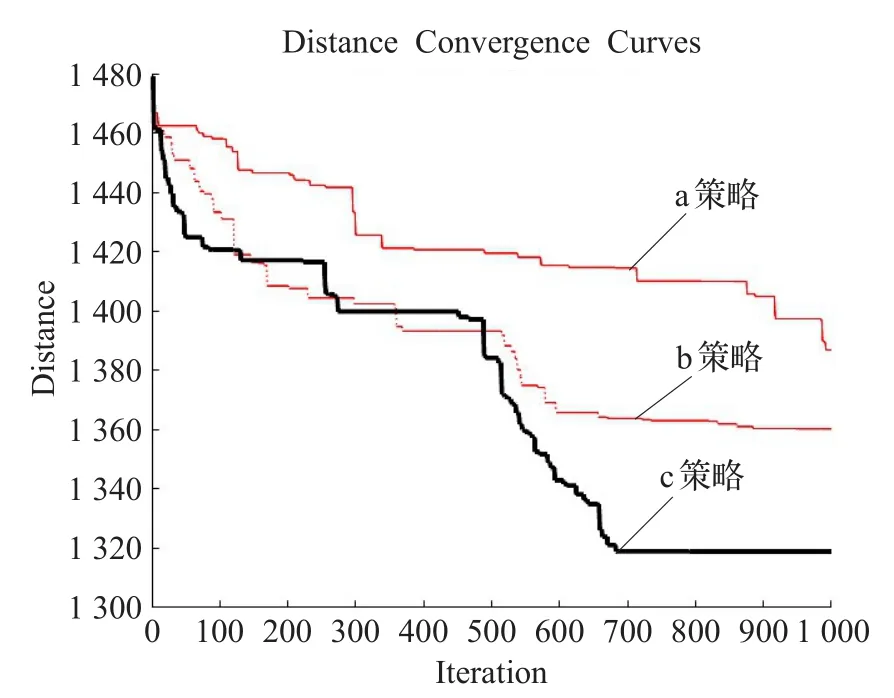
图7 保留策略改进结果对比图

可见，c策略虽然在前期收敛速度并不快，但后期寻优性能明显优于前两者，这是因为c策略的种群多样性优势主要在后期搜索中才能明显表现，可以较好防止收敛于一个局部最优解。

4.1.3 算法综合性能对比

为进一步说明所提算法的优越性，本文将本算法HEA与文献[21]中所提的改进遗传算法IGA进行对比。随机抽取Solomon算例中6个数据进行实验，迭代次数设置为1 000，每个数据重复实验10次，记录10次实验最优解的平均值Avg和其中的最优值Best，并将其与目前已知最优解BestSoFar进行对比。结果见表1，其中“/”之前代表路程长度，之后代表车辆数。

由表1可见，本算法的整体收敛结果较改进遗传算法IGA更优且稳定，与已知最优解的差距更小，说明本算法综合性能较优。

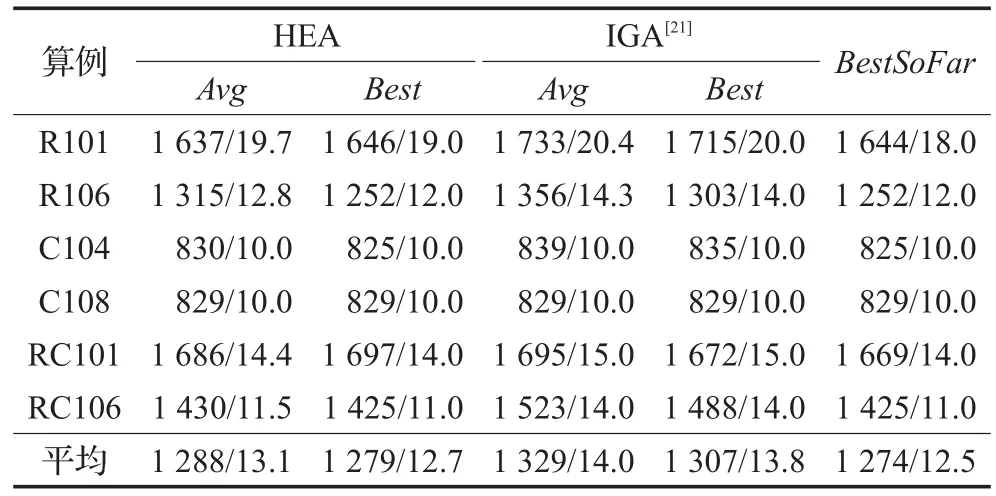
表1 算法综合性能对比结果表

4.2 基于随机需求模型的优化实验及参数敏感性分析

设定不同概率α对模型优化结果会产生很大影响，α设置越大，完成计划的成本越高。α=0.5时，相当于计划满足所有客户的期望需求，则其路径优化结果见图8。最优解收敛迭代曲线见图9，其中黑色实线表示迭代最优解对应的路程，虚线代表种群平均路程，Vn代表最优解对应的车数。求得的计划配送最优路线结果见表2。则计划配送成本为1 156.56+11M=12 156.56。

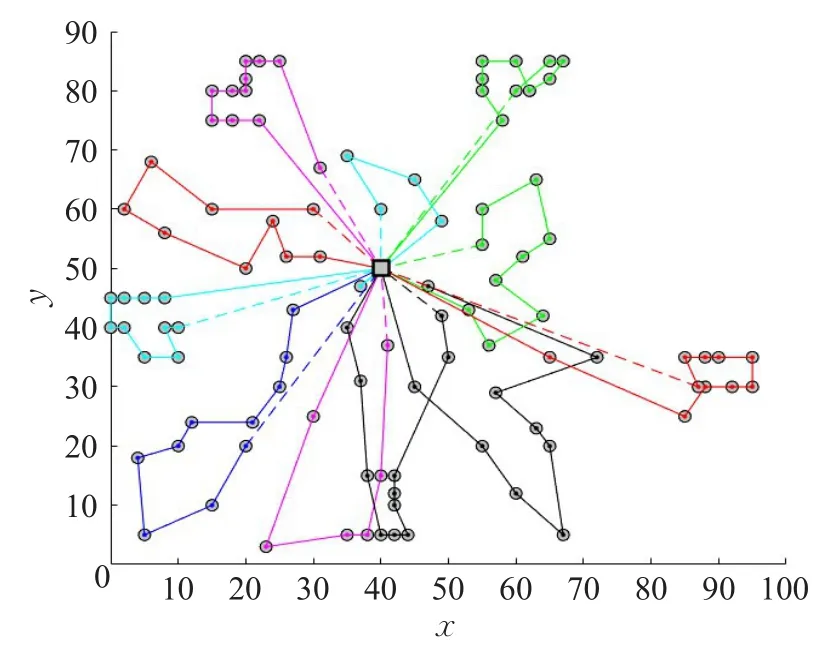
图8 α=0.5时最优计划配送路线图

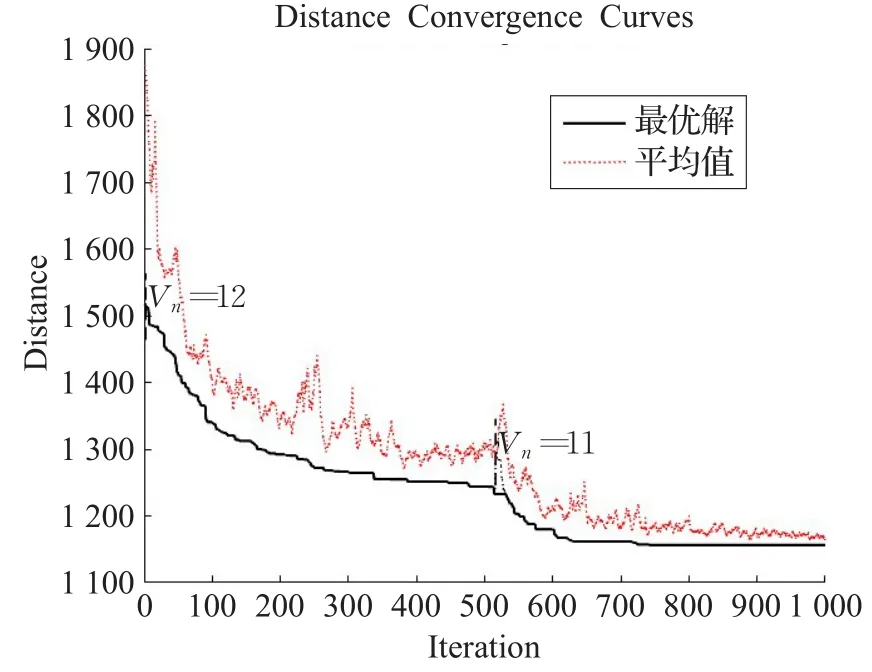
图9 α=0.5时最优解收敛图

表2 α=0.5时计划配送最优路线结果表

为分析计划配送总成本对成功服务概率α的敏感性，再分别设置α的值为0.2、0.4、0.6、0.8，则得到对应的计划配送成本结果见表3。

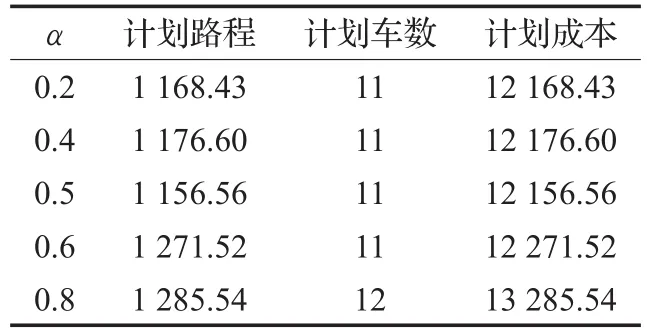
表3 计划配送成本结果表

可见，随着成功服务概率α值的逐渐增加，计划总路程、计划车数以及计划总成本也随之增加。这显然是合理的，因为随着成功服务概率的增加，每个客户的计划需求量都被设为一个较大的值，这样导致需要更多的车和路程去完成配送。但是，虽然服务成功率增加了，物资不必要的浪费也在同样增加，因此需要结合下一步的仿真结果，确定最合理的服务概率α。

4.3 补救策略仿真实验及分析

如前文2.4.2节所述，按计划配送方案进行配送时总会遇到需求量超出的情况，此时服务失败，需要对不满足需求的客户进行补救。分别针对前文所述三种补救策略进行仿真实验。假设给定概率完成服务概率α=0.5，以表1中的优化结果作为计划配送路线，仿真次数Simnum=5 000次，仿真结果见表4～表6。其中，overN表示每段子路径超出容量的平均次数，overV表示每段子路径多派出的平均车次数，overL表示每段子路径多行驶的平均路程，overAt表示每段子路径中到达客户时刻的总延迟时间平均值，overWn表示每段子路径超出截止时间窗的平均客户个数，overWt表示每段子路径违反时间窗的总时间平均值。最后一个指标overC表示每段子路径违反时间窗的惩罚成本，按照下式计算：

表4 策略1的仿真结果统计表

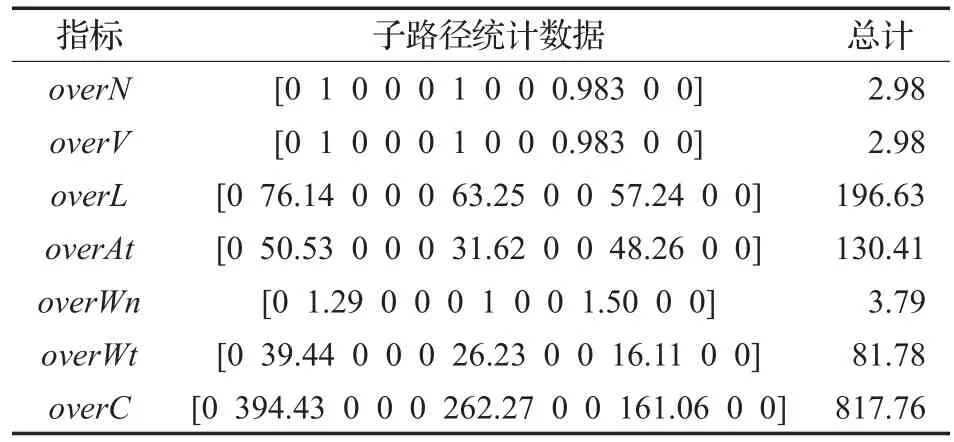
表5 策略2的仿真结果统计表

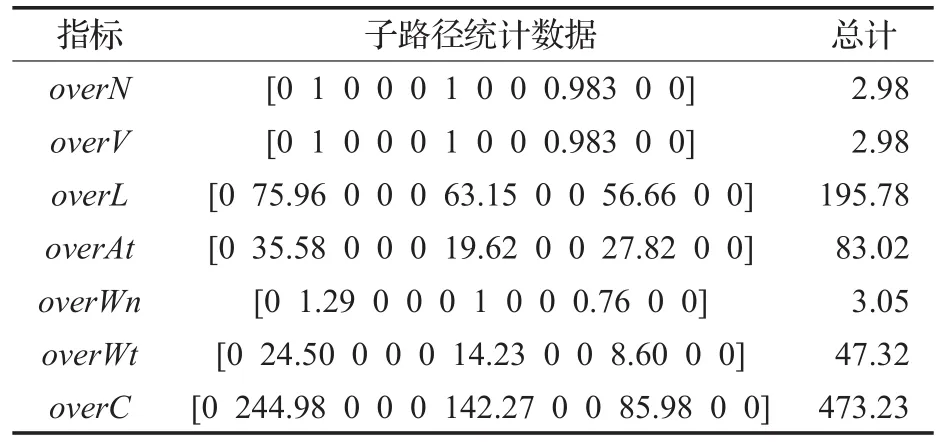
表6 策略3的仿真结果统计表

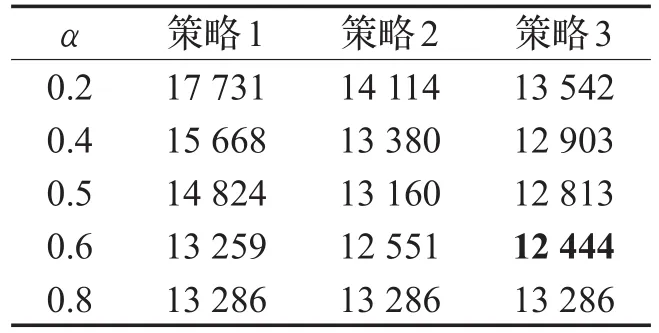
表7 不同α时总成本优化结果表

其中，Ati为车辆到达客户i的时刻，Mt为单位时间的违约惩罚费用，本文设Mt=10。

观察表4～表6可以看出，虽然超出计划配送量的次数overN和新增车次overV相同（均为2.98次），但是策略2较策略1在延迟时间overAt、违反时间约束次数overWn和违反时间overWt三个指标上均有较大降低，因此其更加适应部队客户对时效性的要求，在及时响应客户随机需求的同时满足时间窗约束，因此可靠性也更强；而策略3中对应的后三项指标又有明显降低，因此其时效性和可靠性最强。同时，虽然策略3的overN和overV与策略1、2相同，但在超出路程overL指标上反而较小，说明策略3不但在提高时效性方面优于前两者，在提高经济性方面也有一定优势。

但要注意的是，由于设置容量方差值较小(σi=2)，导致每个子路径最多需要新派一次车，所以并没有出现前文所述车辆浪费的现象，当设置方差为较大数值，例如 σi=30时，用来代表单次超出容量需增加的车次数，则策略1η1=1.015，策略2η2=1.015，策略3η3=1.042，η3较大，可见策略3确实存在车辆浪费的现象。但考虑到时间和路程的节约量较多，而客户需求量方差不会太大的实际情况，采用提前预测、实时反馈、即时发车的第三种补救策略在城市物流配送中显然更具优势。

同时观察最后一项指标惩罚成本overC，发现策略3也是惩罚成本最低的方案。但是，除了计划成本和惩罚成本之外，由于采用补救措施而增加的路程成本也需算进总成本中。而由于原计划的客户并没有完全服务完，新增的车也只是服务了一部分客户，因此可认为每条路线增加的车次成本可以忽略。同时根据4.2节参数敏感性分析结果，总成本还与服务成功概率α有关。因此，总成本应按下式计算：

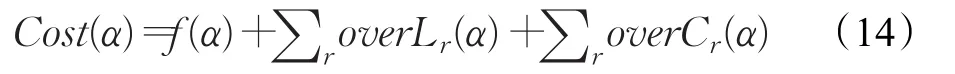
则当设置 α 的值分别为0.2、0.4、0.5、0.6、0.8时计算得到的总成本见表7。

可知，当按照计划服务成功概率α=0.6时的计划路线配送，且采用策略3作为补救策略时的配送总成本最小，为12 444。

5 总结与展望

本文结合现代城市物流配送中客户需求随机且有时间窗的车辆路径问题（VRPSDTW）。构建了机会约束混合整数规划模型，设计了具有多种改进策略的混合进化算法求解该模型，并对服务失败后的三种补救策略进行随机仿真分析，仿真实验表明，采用提前预测是否超出、实时反馈信息给中心、即时派出新车访问下一点的补救策略可以最大程度保证满足客户时间约束，同时还具有降低配送路程的经济优势。最后通过综合计划成本和服务失败的风险成本，确定了最为经济的计划服务成功概率和配送策略。

总的来看，本文有以下几处创新：（1）首次提出了两种新的信息化补救策略，并对三种策略影响总成本的规律进行了深入研究；（2）考虑了时间窗约束，并给出相应的惩罚成本和总成本计算方法；（3）提出多样化变异策略和混合选择的Boltzmann序值选择策略，从而提高了算法性能。

当然，随着客户对服务质量要求的提高以及随机需求的历史数据不易获得的现实情况，更多研究者开始考虑当所有不确定需求均可满足的鲁棒优化问题。其重点和难点是如何定义鲁棒性和不确定集合，这也是本文未来研究的重要方向。

参考文献：

[1]Weyland D.Stochastic vehicle routing from theory to practice[D].Switzerland：University of Lugano，2013.

[2]Lei H，Laporte G，Guo B.The capacitated vehicle routing problem with stochastic demands and time windows[J].Computers&Operations Research，2011，38（12）：1775-1783.

[3]李川.基于混合量子进化算法的随机车辆路径问题的研究[D].杭州：浙江工业大学，2012.

[4]Jr W S，Golden B L.Stochastic vehicle routing：A comprehensive approach[J].European Journal of Operational Research，1983，14（4）：371-385.

[5]Bertsimas D J.A vehicle routing problem with stochastic demand[J].Operations Research，1992，40（3）：574-585.

[6]Teodorović D，Pavković G.A simulated annealing technique approach to the vehicle routing problem in the case of stochastic demand[J].Transportation Planning&Technology，1992，16（4）：261-273.

[7]陆琳，谭清美.一类随机需求VRP的混合粒子群算法研究[J].系统工程与电子技术，2006，28（2）：244-247.

[8]赵燕伟，李川，张景玲，等.一种新的求解多目标随机需求车辆路径问题的算法[J].计算机集成制造系统，2012，18（3）：523-530.

[9]Yee J R，Golden B L.A note on determining operating strategies for probabilistic vehicle routing[J].Naval Research Logistics Quarterly，1980，27（1）：159-163.

[10]Erera A L，Morales J C，Savelsbergh M.The vehicle routing problem with stochastic demand and duration constraints[J].Transportation Science，2010，44（4）：474-492.

[11]Mirmohammadsadeghi S，Ahmed S.Memetic heuristic approach for solving truck and trailer routing problems with stochastic demands and time windows[J].Networks and Spatial Economics，2015，15（4）：1093-1115.

[12]Desrochers M，Lenstra J K，Savelsbergh M W P，et al.Vehicle routing with time windows：Optimization and approximation[C]//Proceedings of the Vehicle Routing：Methods&Studies，F，1987.

[13]Liu B.Uncertainty theory[J].Studies in Computational Intelligence，2015，154（3）：1-79.

[14]Lenstra J K，Kan A H G R.Complexity of vehicle routing and scheduling problems[J].Networks，1981，11（2）：221-227.

[15]Solomon M M.Algorithms for the vehicle routing and scheduling problems with time window constraints[J].Operations Research，1987，35（2）：254-265.

[16]Falkenauer E.A hybrid grouping genetic algorithm for bin packing[J].Journal of Heuristics，1996，2（1）：5-30.

[17]李晨，宁红云.改进的遗传算法选择算子[J].天津理工大学学报，2008，24（6）：1-4.

[18]Coello C A C.Theoretical and numerical constraint-handling techniques used with evolutionary algorithms：A survey of the state of the art[J].Computer Methods in Applied Mechanics and Engineering，2002，191（11）：1245-1287.

[19]张敏.约束优化和多目标优化的进化算法研究[D].合肥：中国科学技术大学，2008.

[20]Pencheva T，Atanassov K，Shannon A.Modelling of a roulette wheel selection operator in genetic algorithms using generalized nets[J].International Journal Bioautomation，2009，13（4）：101-105.

[21]吴天羿，许继恒，刘建永，等.求解有硬时间窗车辆路径问题的改进遗传算法[J].系统工程与电子技术，2014，36（4）：708-713.