一种针对格基后量子密码的能量侧信道分析框架

胡 伟 袁超绚 郑 健 王省欣 李倍倍 唐时博

(西北工业大学网络空间安全学院 西安 710072)

1 引言

公钥密码的安全性受到量子计算的严峻威胁，为此，基于数学困难问题设计的抗量子计算机攻击的后量子密码算法研究受到广泛关注。美国国家标准技术研究所(National Institute of Standards and Technology, NIST)和中国密码学会(Chinese Association for Cryptologic Research, CACR)针对后量子密码进行了系统的研究。后量子密码可分为基于格、基于多变量、基于编码、基于超奇异同源、基于哈希等[1]几种主要类型。其中，构建基于格理论数学困难问题之上的格基后量子密码算法在安全性、密钥尺寸、性能上达到了更好的平衡，是公认最有前景的后量子密码算法之一。虽然格基后量子密码在理论上可抵抗量子计算机攻击，但在算法执行时仍易受到侧信道攻击。

近年来，已有学者对格基后量子密码算法的侧信道攻击展开了研究。2017年，Primas等人[2]对受到掩码保护的格密码进行了单能量迹攻击，其攻击点为数论变换(Number Theoretic Transforms,NTT)。2018年，Kim等人[3]则对Frodo算法的密钥封装机制(Key Encapsulation Mechanism, KEM)进行了单能量迹攻击。2019年，Ding等人[4]和Băetu等人[5]提出了一种选择密文攻击方法，该方法基于冗余的消息编码和密文压缩功能以及大跨度的秘密系数；Pessl等人[6]对Kyber算法加密变换中的NTT变换进行了单能量迹攻击。2020年，Ravi等人[7]针对Kyber等多种格密码算法进行了选择密文攻击，他们的攻击点选择为纠错码和FO(Fujisaki-Okamoto)变换；Amiet等人[8]针对NewHope算法提出了一种单能量迹消息恢复方法，将一条攻击能量迹划分为32个分段，再分别进行模板匹配；Ravi等人[9]将侧信道攻击目标定为存储在内存中的解密消息，利用解密消息1次存储1 bit的特点对解密消息进行恢复。2021年，Ngo等人[10]基于深度学习技术提出了对受到1阶掩码保护的Saber密码算法的侧信道攻击；同年Ngo等人[11]又对受到1阶掩码和洗牌技术保护的Saber KEM的软件实现进行了安全性分析。2022年，Xu等人[12]对Kyber算法使用选定密文进行电磁(Electro Magnetic, EM)侧信道攻击；Tanaka等人[13]针对后量子KEM提出了一种高效的侧信道辅助密钥恢复明文检查攻击(Key-Recovery Plaintext-Checking Attack, KR-PCA)，成功实现了密钥恢复。2023年，Bock等人[14]提出一种新的模板攻击，能够直接从解封装过程的多项式乘法中恢复Kyber的密钥；Guo等人[15]提出了一种针对不可区分选择密文 (INDistinguishability-Chosen Ciphertext Attack, IND-CCA)安全后量子加密方案的密钥侧信道恢复攻击，并对Kyber768的掩码实现进行了攻击。

本文利用秘密多项式系数与能耗的相关性建立了针对格基后量子密码(Post-Quantum Cryptography, PQC)的侧信道攻击框架，提出一种高阶选择密文侧信道攻击方法，实现了对Kyber算法的侧信道攻击分析。与现有针对Kyber的选择密文侧信道攻击[7]相比，本文提出的攻击方法，有效降低了选择密文攻击所使用的密文条数，破解Kyber512和Kyber768密钥所需密文条数分别降低了58.48%和47.5%，表明了高阶选择密文攻击方法的可行性和有效性。

2 Kyber 算法原理

Kyber的安全性基于求解模误差学习问题(Module Learning With Errors, MLWE)的困难性，利用非对称思想实现加密算法和密钥封装协商机制。Kyber公钥加密方案(Public Key Encryption,PKE)处于不可区分选择明文攻击(INDistinguishability-Chosen Plaintext Attack, IND-CPA)安全级别。该方案主要包含密钥生成、加密和解密算法，算法细节如表1所示。

表1 Kyber PKE算法组成

密钥封装协商是基于Kyber PKE来实现通信双方的密钥协商，通过FO变换来构造IND-CCA2安全KEM，称为Kyber KEM。理论上，FO变换有助于保护KEM免受选择密文攻击，FO变换主要涉及解密后的重新加密，能够检测到无效或恶意形成的密文，并在检测时返回失败，但是任何加密算法在真实设备上实现时都会通过侧信道泄露出有关中间值的信息，本文的攻击目标选定在FO变换，本文的攻击同样适用于那些没有使用纠错码的格基密码方案，如NewHope, Frodo, Saber等。

Kyber KEM由密钥生成、加密运算和解密运算3个部分组成，密钥协商具体流程如图1所示。

图1 Kyber KEM 密钥协商

图1展示了通信双方A, B进行密钥协商的过程，A利用Kyber.CCAKEM.KeyGen()算法生成公钥pk和私钥 sk ， 并将公钥p k 发给B。B基于公钥p k利用Kyber.CCAKEM.Enc()算法生成密文c和共享密钥K，B将密文c发送给A，将共享密钥K保留。A在收到B发送的密文c后使用Kyber.CCAKEM.Enc()算法对密文c的正确性进行检查并生成共享密钥K。

3 侧信道攻击模板构建

3.1 密文筛选条件

算法1展示了基于中间变量(u,v,s)完成解密的方法。解码密文c得到多项式系数(u,v)，解码私钥sk得 到秘密多项式s的系数，通过Poly_to_Msg即可获得信息m′。可见，变量(u,v)决定了密文c，(s k,c)唯一确定了信息m′，而s k又与s直接相关，这为实现对Kyber的侧信道攻击分析提供理论依据。

令ku=u[0],kv=v[0]，u和v的其他系数为0。则消息m′可由式(1)按比特位进行解密

根据式(1)，消息m′仅 依赖于s[0]，因此可通过筛选ku和kv使 得消息m′和s[0]满足式(2)

因此，攻击者可通过选择(ku,kv) 生成密文c，使解密消息m′=0 或m′=1， 进而唯一确定s[0]的值。类似地，攻击者通过改变u中非0系数的位置，将ku的 值依次赋给u[0],u[1], ···,u[n-1]，同时将此时多项式的其他系数赋为0。按对应顺序恢复s[0],-s[n-1],-s[n-2], ···, -s[2],-s[1] 后可获得私钥s k。

算法1 Kyber.CPAPKE.Dec(sk, c)

在Kyber.CPAPKE.KeyGen()算法中，多项式s的系数由一个中心二项分布函数CBDη产生。而s的每一个系数的范围在[-η,η]之 间，其中η=2或η=3 。 经多次实验搜索(ku,kv) ，使得s∈[-η,η]时对应的解密信息m′=0或m′=1，如表2所示。攻击者可利用表2中的密文条件实现对Kyber的侧信道攻击。

表2 Kyber的选择密文攻击表

3.2 创建攻击模板

构建选择密文攻击表和创建攻击模板的前提是攻击者已知密码算法的实现细节，通过选择密文、执行算法、采集能量迹来建立模板和选择密文攻击表。攻击者首先选择(ku,kv) 生成密文c，在此密文条件下，解密信息m′=0 或m′=1，再根据解密信息m′的 值和多项式s的系数的值确定选择密文攻击表，同时在执行Kyber的密钥解封装过程中，分别采集m′=0 和m′=1两种情况下的能耗曲线以创建攻击模板。攻击模板构建流程如图2所示，通过对采集的能量迹进行去噪和兴趣点筛选，得到m′=0和m′=1的模板迹。

图2 攻击模板建立流程

建立攻击模板时，需对采集到的能量迹进行分组，按组计算平均能量迹，以降低噪声。最后采用测试矢量泄漏评估(Test Vector Leakage Assessment,TVLA)方法筛选兴趣点。

4 侧信道攻击方法及框架

4.1 高阶选择密文攻击

模板匹配时，普通选择密文方法[7]需要2η+1条密文来破解多项式s的系数。本文首次提出了高阶选择密文攻击方法，基于密文特点，对密文进行选择，缩小多项式s系数的候选值范围；再次挑选密文使得候选值不断缩小，直至候选值唯一，具体流程如图3所示。

图3 高阶选择密文攻击分析流程图

经η个选择密文的能量迹完成模板匹配后，若多项式s的系数唯一，则说明攻击成功。若系数不唯一，则可将s的范围缩小到N个候选值集合中，第i个候选值集合的阶数用ni表示，则每个集合最多再需分析ni-1条密文即可确定密钥信息，可显著降低攻击所需要的密文条数。

4.2 秘密系数破解方法

攻击者可以选择输入密码设备的密文，运行Kyber密钥解封装模块并采集能量迹，利用选择密文攻击表中的(ku,kv) 成密文c；攻击者可通过输入不同的密文c获取对应能量迹，将能量迹与攻击模板进行匹配，并对照选择密文攻击表分析多项式s的系数。

在图3所示的攻击流程中，通过计算目标迹与攻击模板的欧氏距离进行匹配。与目标迹距离小的模板相关性高，该模板对应的数值可认定为目标迹对应的值，结合选择密文攻击表和高阶选择密文攻击方法即可破解对应的多项式系数。

4.3 密钥恢复方法

CPAPKE.KeyGen()函数中，可由多项式s经过相关变换生成私钥sk

其中，q为算法参数，NTT()函数为数论变换函数，Encode12()函数为编码函数，可以将多项式系数转化为字节流。这些参数和函数均为已知，因此在破解多项式s系数后可以得到私钥s k。

在算法Kyber.CCAKEM.Dec()中利用攻击得到的私钥s k 对 正确密文c解密得到m′

对m′进行编码

其中h=H(pk)，G和H为哈希函数。使用公钥加密m′获 得密文c′

若攻击所得私钥 sk 正 确，此时的c′应和正确密钥c相等。此时，进行相关变换可得到共享密钥K

其中KDF为一种哈希函数。上述由私钥s k得到共享密钥K的变换过程中所需要的参数和函数均为已知，因此可由私钥s k 破解出共享密钥K。

5 实验与结果

5.1 实验设置

实验环境如表3所示。使用C语言在stm32开发板上实现Kyber密钥协商算法，使用Pico示波器采集能量迹，使用python对能量迹进行分析，实现高阶选择密文侧信道攻击。

表3 测试案例实验环境

高阶选择密文攻击分析流程如图4所示，首先需根据Kyber512和Kyber768算法原理，筛选符合条件的密文c使得运行解封装函数时中间值m′=0和m′=1， 分别采集密文解密时的能量迹，建立m′=0和m′=1的攻击模板。然后，采集目标迹，根据目标迹与模板的匹配程度，破解秘密多项式s的系数，使用密钥生成算法Kyber.CPAPKE.KeyGen()恢复私钥s k， 最后利用得到的s k恢 复共享密钥K。

图4 高阶选择密文攻击分析流程

5.2 Kyber512侧信道攻击

在对Kyber512进行侧信道攻击时首先选择特定的密文构建选择密文攻击表。Kyber512中变量η=3 ， 因此多项式s的系数为–3～3。文献[7]的攻击方案，需要7种密文才能破解Kyber512的所有多项式系数，本文对其进行了优化仅需要6种，Kyber512选择密文攻击表如表4所示。

表4 Kyber512选择密文攻击表

采集Kyber512解密过程中运行哈希函数G时的能量迹。使用两组密文数据，在m′=0 和m′=1的情况下，分别采集10 000条能量迹；对这两组能量迹按每200条取平均后转换为50条平均能量迹作为模板。取平均能量迹降低了噪声的影响，使构建的攻击模板更加精确，有利于提高攻击结果的准确性。

筛选兴趣点时需对比m′=0 和m′=1的平均能量迹。如图5(a)所示，红色为m′=0时哈希函数G的能量迹；蓝色为m′=1时哈希函数G的能量迹。使用TVLA方法对比两组平均能量迹的差异，如图5(b)所示，设置阈值为4，选择TVLA值大于4或小于–4的点作为兴趣点，建立m′=0和m′=1的模板。

图5 Kyber512平均能量迹和兴趣点筛选

攻击者可选择密文输入，运行Kyber512密钥协商算法的解密函数，无需获知密码算法实现细节。使用高阶选择密文方法恢复多项式s所有的系数。Kyber算法中多项式s的每个系数由中心二项分布函数CBDη产生。当η=3时 ，s的系数为–3,–2,–1,0,1,2,3，其概率分别为1/64, 6/64, 15/64, 20/64,15/64, 6/64, 1/64。当使用高阶选择密文方法有策略地对密文进行选择时，对于出现频率高的系数应尽可能使用更少的密文，Kyber512高阶选择密文方法如图6所示。

图6 Kyber512高阶选择密文方法

对于多项式s，首先使用(3 120, 2 380)和(3 120,1 130)构建密文进行攻击，根据m′的值可以将其分为3个集合，即(–3, –2, –1),(0)和(1, 2, 3)。再对集合(–3, –2, –1)和(1, 2, 3)加以区分，直至破解出系数值。由图6可知当系数为0时需要2条密文，当系数为–1和1时需要3条密文，当系数为–3,–2,2,3时需要4条密文。系数出现的频率越高攻击所需的密文越少，可利用这一特性降低所需的密文数量。在破解出多项式s的所有多项式系数后，可再根据4.3节介绍的密钥恢复算法得到私钥s k和 共享密钥K。

5.3 Kyber768侧信道攻击

类似地选择特定密文构建选择密文攻击表。Kyber768中的变量η=2， 因此s的系数为–2～2。文献[7]的攻击方案，需要5种密文才能破解Kyber768的所有多项式系数，本文仅需要4种密文，Kyber768选择密文攻击表如表5所示。

表5 Kyber768选择密文攻击表

Kyber768算法攻击的能量迹采集方法、平均能量迹计算方法以及兴趣点筛选方法均与Kyber512算法攻击过程类似。如图7(a)所示，红色为m′=0时哈希函数G的平均能量迹，蓝色为m′=1时哈希函数G的平均能量迹。如图7(b)所示，设置阈值为2，选择能量迹中TVLA值大于2或小于–2的点作为兴趣点。

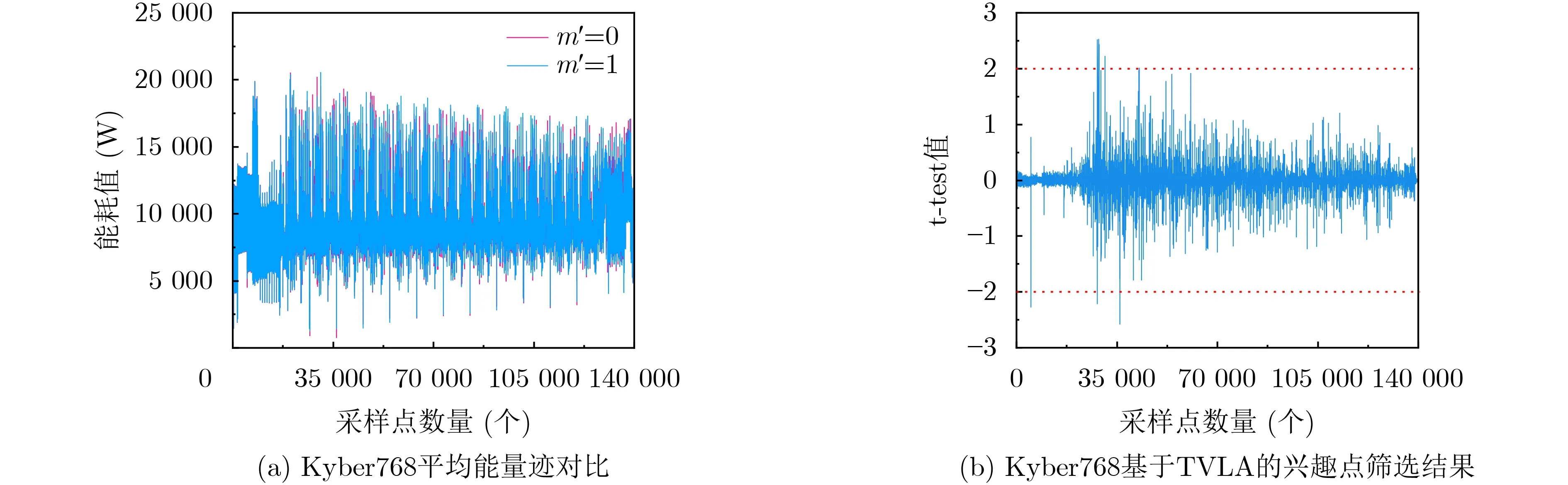
图7 Kyber768平均能量迹和兴趣点筛选

使用高阶选择密文方法对多项式s的系数进行恢复。当η=2时s的系数为–2,–1,0,1,2，其概率分别为1/16,4/16,6/16,4/16,1/16，Kyber768高阶选择密文方法如图8所示。

图8 Kyber768高阶选择密文方法

对于多项式的一个系数s首先使用(10,740)和(10,2 400)构建密文进行攻击，根据m′的值可以将其分为3个集合分别是(–2, –1),(0),(1, 2)。之后再使用(110, 530)和(110, 2 610)分别对集合(–2, –1)和(1,2)加以区分。由图8可知当系数为0时需要2条密文，当系数为–2,–1,1,2时分别需要3条密文。

利用同Kyber512相同的方法，在多项式s的系数完全恢复后再利用s对 私钥s k进行恢复，之后可再利用私钥s k 对 共享秘钥K进行恢复。

5.4 性能分析

本文成功建立了针对格基PQC的侧信道攻击框架，并首次提出了一种高阶密文选择方法，在攻击过程中通过利用密文的特点，改变选择密文的方式可以极大减少攻击过程所需要的密文。以Kyber512和Kyber768算法为例，成功恢复出两种密码算法的多项式s的系数，以及加密私钥s k和共享密钥K，验证了该方法的可行性和有效性。

另外，本文所提方法在攻击所针对的密码算法数量、攻击成功率、攻击所用密文数量等方面均有优势。

在攻击所针对的密码算法方面，本文的攻击方法不仅可以对Kyber进行攻击，还可以对NewHope,Frodo, Saber等多种不使用纠错码的格基后量子密码进行攻击，攻击覆盖面较广。

在攻击成功率方面，本文方法对Kyber512和Kyber768的攻击成功率均可达到99%。 表6展示了不同方案攻击的密码算法及成功率。

表6 不同方案攻击的密码算法及成功率

在攻击所使用密文数量方面，本文对于文献[7]中的方法进行了改进，可以使用更少的密文恢复出多项式s的系数。文献[7]、文献[9]和文献[13]均对Kyber512进行了侧信道攻击。攻击s的所有位置，文献[7]中的方法需要3 584条密文，本文中所提出的高阶选择密文攻击方法仅需1 488条密文，降低了约58.48%。文献[9]针对Kyber512进行攻击需要128 000条密文。文献[13]针对Kyber512进行攻击需要1 728条密文。文献[7]、文献[13]均对Kyber768进行了侧信道攻击。攻击s的所有位置，文献[7]中的方法需要3 840条密文，本文中所提高阶选择密文攻击方法仅需2 016条密文，降低约47.5%。文献[13]针对Kyber768进行攻击需要3 456条密文。文献[6]和文献[14]对Kyber进行了单能量迹侧信道攻击，在此不做对比。图9(a)和图9(b)分别展示了不同方案攻击Kyber512和Kyber768使用的密文数。

图9 不同方案攻击Kyber使用的密文数柱形图

6 结论

本文建立了一种针对格基PQC的侧信道攻击框架，并提出了高阶选择密文侧信道攻击方法。与文献[7]的选择密文攻击方法相比，本方法恢复Kyber512和Kyber768的密钥所需密文数分别降低了58.48%和47.5%，攻击成功率均达到99%。通过将本文方法应用于NewHope, Frodo, Saber等多种格基后量子密码算法，验证了本文所提方法在适用密码算法数量、攻击成功率、攻击所需密文数量等方面均有显著优势，能够为评估后量子密码算法实现侧信道安全风险提供支撑。