云微物理特性及云滴有效半径参数化：一次降水层状云的飞机观测资料结果

解小宁，王昭生，王红丽，岳治国

（1.中国科学院地球环境研究所 黄土与第四纪地质国家重点实验室，西安 710061；2.陕西广播电视大学，西安 710119；3.陕西省人工影响天气办公室，西安 710015）

云微物理特性及云滴有效半径参数化：一次降水层状云的飞机观测资料结果

解小宁1，王昭生1，王红丽2，岳治国3

（1.中国科学院地球环境研究所 黄土与第四纪地质国家重点实验室，西安 710061；2.陕西广播电视大学，西安 710119；3.陕西省人工影响天气办公室，西安 710015）

全球及区域气候模式中云滴有效半径的参数化对于理解云的辐射效应特别是气溶胶间接效应是非常重要的。本文利用延安地区（位于中国西北地区）一次降水层状云的飞机观测资料，首先给出该次过程的云微物理特性包括云滴数浓度（Nc），云水含量（Qc），云滴的半径（Rm），体积半径（Rv），以及有效半径（Re），云滴谱离散度（ε）以及Re/Rv比值因子β；并指出云滴谱离散度ε与云滴数浓度Nc有着很好的递减关系式，所对应的关系式可以表述为ε= 0.579 - 7.42×10-4Nc+ 4.2×10-7Nc2。进一步，发现云滴尺度谱采用Lognormal分布函数，Gamma分布函数以及Weibull分布函数所参数化的云滴有效半径与观测结果较为一致。值得指出的是，基于Lognormal分布函数的参数化能够更好地描述云滴有效半径。该云滴有效半径的参数化结果将会加强对于气溶胶在中国西北地区间接辐射强迫的认识。

云滴尺度谱分布；云滴谱离散度；云滴有效半径

云作为地气系统最重要的组成部分之一，覆盖了地球表面的60%以上，极大反射和吸收太阳短波和地面长波辐射，进而影响地气系统的辐射平衡；以及影响局域、全球降水的时空分布。云滴有效半径定义为云滴尺度谱分布的3阶积分与2阶积分的比值，直接决定着云光学厚度、单次散射比和非对称因子等重要的云光学物理量（e.g., Martin et al，1994；Liu and Daum，2002；Deng et al，2009；Xieand Liu，2013；解小宁等，2015）。

云滴有效半径（Re）的参数化对于天气气候模式，有着非常重要的作用。因此，精确参数化Re是目前非常热门的话题，也是减少气候模式中云描述不确定性的一个重要途径。Slingo（1990）指出云滴有效半径从10 μm减少到8 μm基本上就可以抵消2倍CO2带来的温室效应。然而，在目前的大部分天气气候模式中，云滴有效半径都采用常数或者是云滴数浓度与云水含量的函数来描述。一般的，云滴有效半径Re可以写成如下体积半径Rv的表达式，

β是Re/Rv比值因子。利用飞机的观测结果，Martin et al（1994）给出β是常数，在大陆和海洋上有差异，大陆对应β值比海洋的β值要大一些。在其他的飞机观测研究中，同时也证明β作为常数，可以有效地描述云滴有效半径（Deng et al，2009；Nair et al，2012）。另外，Deng et al（2009）同时也指出，利用Rv的多项式拟合的参数化，可以减少与观测结果的偏差。另外，通过假设云滴的尺度谱分布，可以解析得到Re/Rv比值因子β（例如，Liu and Daum，2000；Liu et al，2002）。通常云滴尺度谱分布可以采用Lognormal 分布函数，Weibull 分布函数，Gamma分布函数来描述。本研究将利用不同的云滴谱尺度分布函数得到的β以及常数β描述的云滴有效半径与飞机观测资料进行对比分析。

本文将利用延安地区一次降水层状云的飞机观测得到的云滴尺度谱分布，主要是针对暖云部分，给出该次过程的云微物理特性包括云滴数浓度，云水含量，云滴的半径，体积半径，以及有效半径，云滴谱离散度以及Re/Rv比值因子，并得到云滴谱离散度与云滴数浓度的关系。进一步，得到基于不同云滴尺度谱分布函数（Lognormal函数，Gamma函数以及Weibull函数）所描述的云滴有效半径的理论参数化，并与飞机观测得到的云滴有效半径进行对比分析。

1 个例描述及云微物理性质

本节中，将利用2003年9月17号延安一次降水层状云的飞机观测的云滴尺度谱分布，研究该次过程的云微物理特性及云滴谱离散度的变化规律。具体的飞机飞行路径、时间以及气象条件在文献（王扬锋等，2007）中可以看到。该次飞机观测所用的仪器是PMS粒子测量系统的FSSP-100探头，该探头所测得的云滴直径范围2— 47 μm。在这里，云区域定义为云滴数浓度大于等于10 cm-3，流体水含量大于等于0.01 g · m-3（Gultepe et al，1996）。云微物理特性包括云滴数浓度（Nc），云水含量（Qc），云滴的半径（Rm），体积半径（Rv），以及有效半径（Re），云滴谱离散度（ε）以及Re/Rv比值因子β。这些云微物理量分别定义为如下的数学表达式：

其中：ni是FSSP-100观测到第i个档粒子数，ri是第i个档半径的上限和下限半径的平均值，ρw是流体水的密度，ρw=1g · cm-3。

表1给出了该次过程云微物理量的统计值，包括云滴数浓度Nc，云水含量Qc，平均半径Rm，平均体积半径Rv，平均有效半径Re，以及相对离散度ε，和Re/Rv比值因子β的最大值（Max），平均值（Mean），中值（Median），及标准偏差（STDEV）。该次降水层状云观测结果显示，云滴数浓度Nc的最大值为561 cm-3，平均值为183 ± 91 cm-3。云水含量Qc的最大值为0.129 g · m-3，相应的平均值0.034 ± 0.021 g · m-3。平均半径Rm的最大值为5.33 μm，而平均值为2.96 ± 0.63 μm。平均体积半径Rv为6.24 μm，平均值为3.60 ± 0.77 μm。云滴有效半径Re为7.23 μm，平均值为4.38 ± 0.97 μm。云滴谱离散度ε的最大值为0.67，所对应的平均值0.46 ± 0.08。Re/Rv因子β最大值为1.52，平均值为1.22 ± 0.07。

图1a 给出了云滴谱离散度ε与云滴数浓度Nc的依赖关系。在该图中，云区域定义为云滴数浓度大于等于10 cm-3，流体水含量大于等于0.001 g ·m-3。在云滴数浓度比较低的情况下（50 cm-3），云滴谱离散度有个较大的变化范围，在0—0.7变化；而在云滴数浓度比较高的情况下，云滴谱离散度的变化范围则小的多，几乎变成ε=0.3左右的一个常数。值得指出的是，该云滴谱离散度的变化规律与Zhao et al（2006）给出的结果是完全一致的。从该图可以看出，云滴谱离散度随着云滴数浓度的变化规律，并不能用简单的数学公式描述。但是当定义云区域的最低流体水含量Lc≥0.01 cm-3时，就会出现非常有意义的结果（图1b）。该图显示，云滴谱离散度ε与云滴数浓度Nc有着明显的递减关系。在云滴数浓度较低时（50 cm-3），云滴谱离散度数值在0.6左右；而当云滴数浓度较高时，云滴离散度在0.3左右。因此，云滴谱离散度可以用ε =0.579-7.42×10-4Nc+4.2×10-7Nc2关系式进行很好的描述。

表1 云微物理特性的统计表，包括云滴数浓度Nc，云水含量Qc，平均半径Rm，平均体积半径Rv，平均有效半径Re，以及相对离散度ε，和Re/Rv比值因子βTab.1 Statistics of the cloud microphysical properties including cloud droplet number concentrationNc, cloud liquid water contentQc, the mean radiusRm, mean volume radiusRv, effective radiusRe, relative dispersionεandRe/Rvprefactorβ

图1 云滴谱离散度ε与云滴数浓度Nc的依赖关系，云区域定义为Nc≥10 cm-3，以及（a）Qc≥0.001 g · m-3，（b）Qc≥0.01 g · m-3Fig.1 Relationships between cloud droplet relative disperisonεand droplet concentrationNc. The aera of clouds is de fi ned asNc≥10 cm-3, and (a)Qc≥0.001 g · m-3, (b)Qc≥0.01 g · m-3

从图1a和1b的差别来看，流体水含量在0.001 ＜Lc＜ 0.01 cm-3范围时，主要对应的是云滴数浓度较少，谱离散度较小的散点。流体水含量很小时，云滴的尺度谱分布可能仅仅依赖于云滴初始的形成性质，与碰撞增长等其他的微物理过程没有关系。因而，此时对应的云滴谱离散度非常小。该区域或许对应于云的边缘区域，对于云整体的辐射特性以及降水过程的影响是非常微小的。因此，可以认为图1b更能描述该次降水层状云的云滴谱离散度的变化规律。

从上述分析结果来看，用云滴数浓度进行参数化云滴谱离散度是合理的。研究结果显示，这次延安地区降水层状云的云滴谱离散度随着云滴数浓度增加存在明显的递减趋势。该结果与 Ma et al（2010）的变化规律是一样的；而与Martin et al（1994）和Liu and Daum（2002）的变化规律是截然相反的（可以从文献Xie et al（2013）中看到不同的云滴数浓度与离散度的关系式）。

2 云滴有效半径的参数化

2.1 基于不同云滴尺度谱函数的云滴有效半径的理论参数化

云滴有效半径通常可以被定义为下述的解析表达式：

其中：ρw是流体水密度，Lc和Nc分别表示云水含量（g · m-3）及云滴数浓度（cm-3）。其中β就是Re/Rv比值因子，定义为方程（10）的表达式。β值通常被简单地认为是常数（Martin et al，1994；Deng et al，2009；Nair et al，2012），用来描述云滴的有效半径。另外，可以通过假定云滴尺度谱分布，解析得到β的函数（例如，Lognormal分布函数，Gamma分布函数和Weibull分布函数）。下文回顾基于不同的解析尺度谱分布函数给出的Re/Rv比值因子β的表达式 （Liu et al，2002），并进一步与观测得到的β进行对比。

云滴尺度谱分布可以被描述为Lognormal分布函数：

其中：r表示云滴的半径；σ为谱型的宽度，直接与相对离散度有关；Nc为单位体积的总云滴数浓度；rg是平均半径。云滴谱的相对离散度ε可以表达为σ的函数：

基于Lognormal分布函数（11），根据方程（10）β的定义，可以得到：

另外，云滴尺度谱分布也可以用Gamma分布函数来描述，该分布函数的具体表达式如下：

其中：参数μ是谱型相关的参数，直接与云滴谱相对离散度有关。云滴谱的相对离散度ε是μ的函数，表达式如下：

基于Gamma分布函数（14），根据方程（10）β的定义，同样也可以得到该分布函数相应的β：

同样也有很多观测研究表明，Weibull分布函数也可来用来描述云滴尺度谱分布：

其中：参数q是谱型参数，与相对离散度直接相关。云滴谱的相对离散度ε可以描述为q的函数：

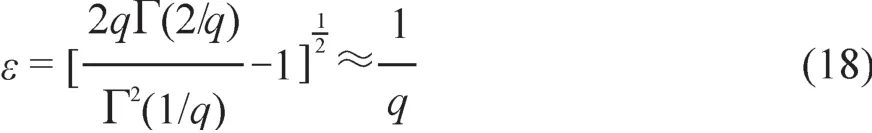
基于Weibull分布函数（17），根据方程（10）β的定义，可以得到该分布函数相应的β的表达式，具体如下：

图2给出了不同的云滴尺度谱分布函数得到β的表达式（13）、（15）和（19），以及与该次飞机观测结果的对比。该图显示，3种不同的云滴尺度谱分布函数得到的β都能较好地反映观测结果，都具有较大的R2值。从R2值的大小比较来看，Lognormal分布函数给出了最大的R2值，达到0.81。次之是 Gamma分布函数，R2值为0.70，最小的R2值是Weibull分布函数给出的，为0.62。

图2 基于观测结果，以及基于不同云滴尺度谱分布函数（Lognormal分布函数， Gamma分布函数以及Weibull分布函数）得到Re/Rv比值因子β与相对离散度ε的关系Fig.2 Relationships betweenRe/Rvprefactorβand relative dispersion derivedεfrom observations, and different cloud droplet size distributions (Lognormal function，Gamma function and Weibull function)

2.2 云滴有效半径的理论参数化与观测结果对比

在上个小节中，基于不同云滴尺度谱分布函数，解析得到了Re/Rv比值因子β；并进一步与观测得到结果进行对比，显示了这3种云滴尺度谱分布函数都可以较好地描述该参数β。在本小节中，利用解析得到的β表达式描述的云滴有效半径Re（Re=βRv），与观测取得的云滴有效半径进行对比，来确定云滴有效半径的理论参数化是否能很好地描述云滴有效半径。

图3给出了基于不同的云滴尺度谱分布函数以及β= 1.22，理论给出的云滴有效半径参数化与观测结果的对比。该图显示，4种不同的理论参数化方案（其中包括β为常数）基本上都可以反映观测到的云滴有效半径。虽然β为常数的参数化方案（图3d）也可以描述观测到的结果，但是该方案给出的云滴有效半径与观测结果之间的相对误差较大（相应值达到6%）。相较于β为常数的参数化方案，另外3种不同的云滴尺度谱分布函数给出参数化方案则更为准确地描述了观测到的云滴有效半径。对于Lognormal分布函数，Gamma分布函数以及Weibull分布函数，得到的云滴有效半径与观测结果之间的相对误差分别为1%，3%，和3%。

因此，相对于β为常数的参数化方案，这3种云滴尺度谱分布函数（Lognormal分布函数，Gamma分布函数以及Weibull分布函数）给出的参数化方案可以更好地描述云滴的有效半径。值得指出的是，其中Lognormal分布函数的参数化方案给出的云滴有效半径与观测结果之间的相对误差最小。因此，Lognormal分布函数给出的参数化方案能够更好地描述云滴有效半径。

图3 基于不同云滴尺度谱分布（Lognormal分布函数，Gamma分布函数，Weibull分布函数，以及β=1.22）得到云滴有效半径与观测结果的对比其中RD为与观测结果对比的相对误差（，ai是观测值，bi是参数化计算值，N是总的数据个数）Fig.3 Comparison of parameterization of effective radius derived from different cloud droplet size distributions (Lognormal function, Gamma function and Weibull function) with observations RD is the relative differences compared to observations ((,aiis the observed value,biis value derived from parameterization, andNis the total number.)

3 结语与展望

本文针对延安地区（位于中国西北地区）一次降水层状云的飞机观测资料得到的云滴尺度谱分布进行分析。首先得到该次过程中的云微物理特性的统计值（最大值，平均值，中值及标准偏差），其中包括云微物理量云滴数浓度（Nc），云水含量（Qc），云滴的半径（Rm），体积半径（Rv），以及有效半径（Re），云滴谱离散度（ε）以及Re/Rv因子β；并指出云滴谱相对离散度ε与云滴数浓度Nc有着很好的递减关系式，所对应的关系式可以表述为ε =0.579 - 7.42×10-4Nc+4.2×10-7Nc2。进一步发现云滴尺度谱的Lognormal分布函数，Gamma分布函数以及Weibull分布函数所描述的云滴有效半径与观测结果较为一致。而其中Lognormal分布函数的参数化方案给出的云滴有效半径与观测结果之间的相对误差最小，显示其能够更好地描述云滴有效半径。该结果将会加强对于气溶胶在中国西北地区间接辐射强迫的认识。

值得指出的是，本文的参数化结果都是基于延安地区的一次降水层状云的飞机观测结果。但云过程是非常复杂的过程，与气溶胶物理化学特性以及大气环境（包括大气湿度，稳定度）等有着密切的关系（Liu and Daum，2002；Liu et al，2002；解小宁等，2015），下一步需要更多时次及不同云类型等的飞机观测资料，来研究云微物理特性以及云滴有效半径的参数化。

王扬锋, 雷恒池, 樊 鹏, 等. 2007. 一次延安层状云微物理结构特征及降水机制研究 [J].高原气象, 26(2): 388 – 395. [Wang Y F, Lei H C, Fan P, et al. 2007. Analyses on microphysical characteristic and precipitation mechanism on stratiform cloud in Yan’an [J].Plateau Meteorology, 26(2): 388 – 395.]

解小宁, 刘晓东, 王昭生. 2015. 云滴谱离散度对气溶胶间接效应影响的研究进展 [J].地球环境学报, 6(2): 127 – 134. [Xie X N, Liu X D, Wang Z S. 2015. Review of influence of cloud droplet spectral dispersion on aerosol indirect effects [J].Journal of Earth Environment, 6(2): 127 – 134.]

Deng Z, Zhao C, Zhang Q, et al. 2009. Statistical analysis of microphysical properties and the parameterization of effective radius of warm clouds in Beijing area [J].Atmospheric Research, 93: 888 – 896.

Gultepe I, Isaac G, Leaitch W, et al. 1996. Parameterizations of marine stratus microphysics based on in situ observations: implications for GCMS [J].Journal of Climate, 9: 345 – 357.

Liu Y, Daum P H, Chai S K, et al. 2002. Cloud parameterizations, cloud physics, and their connections: An overview [M]//Pandalai S G. Recent Research Developments in Geophysics. Trivandrum: Research Signpost Publisher, 119 – 142.

Liu Y, Daum P H. 2000. Spectral dispersion of cloud droplet size distributions and the parameterization of cloud droplet effective radius [J].Geophysical Research Letters, 27: 1903 – 1906.

Liu Y, Daum P H. 2002. Indirect warming effect from dispersion forcing [J].Nature, 419: 580 – 581.

Ma J, Chen Y, Wang W, et al. 2010. Strong air pollution causes widespread haze-clouds over China [J].Journal of Geophysical Research, 115, D18204, doi: 10.1029/2009JD013065.

Martin, G M, Johnson D W, Spice A. 1994. The measurement and parameterization of effective radius of droplets inwarmstratocumulus clouds [J].Atmospheric Research, 51: 1823 – 1842.

Nair S, Sanjay J, Pandithurai G, et al. 2012. On the parameterization of cloud droplet effective radius using CAIPEEX aircraft observations for warm clouds in India [J].Atmospheric Research, 108 : 104 – 114.

Slingo A. 1990. Sensitivity of the earth’s radiation budget to changes in low clouds [J].Nature, 343: 493 – 51.

Xie X N, Liu X D, Peng Y, et al. 2013. Numerical simulation of clouds and precipitation depending on different relationships between aerosol and cloud droplet spectral dispersion [J].Tellus B, 65, 19054, doi: 10.3402/tellusb. v65i0.19054.

Xie X N, Liu X D. 2013. Analytical studies of the cloud droplet spectral dispersion influence on the first indirect aerosol effect [J].Advances in Atmospheric Sciences, 30(5): 1313 – 1319.

Zhao C, Tie X, Brasseur G, et al. 2006. Aircraft measurements of cloud droplet spectral dispersion and implications for indirect aerosol radiative forcing [J].Geophysical Research Letters, 33, L16809, doi: 10.1029/2006GL026653.

Cloud microphysical properties and parameterization of cloud droplet effective radius from aircraft measurements: aircraft observational results from a stratiform precipitation cloud

XIE Xiaoning1, WANG Zhaosheng1, WANG Hongli2, YUE Zhiguo3
(1. State Key Laboratory of Loess and Quaternary Geology, Institute of Earth Environment, Chinese Academy of Sciences, Xi’an 710061, China; 2. Shaanxi Radio & TV University, Xi’an 710119, China; 3. Weather Modi fi cation Of fi ce of Shaanxi Province, Xi’an 710015, China)

Background, aim, and scopeCloud is one of the most important components of the Earthatmosphere system, which covers approximately half of our planet surface and affect its radiative energy balance, as well as the global and regional spatial-temporal distribution of surface precipitation. The treatment of radiative properties of clouds is very important in numerical models that can simulate the expected climate change produced by increasing concentrations of anthropogenic greenhouse gases and aerosols. The radiative properties of clouds (including optical thickness, the single scattering albedo, and the asymmetry factor) are mainly dependent on the cloud droplet effective radius, which is defined as the ratio of the third to secondmoment of the cloud droplet size distribution. Hence, the parameterization of cloud droplet effective radius in the various climate and weather models is fundamental to understanding the radiative effects of clouds, and its accurate paremeterization is also especially of importance to evaluate the aerosol indirect effect and can reduce the uncertity of the aerosol indirect effect.Materials and methodsHere, we use an observed data about the cloud droplet size distribution, which is derived from aircraft measurements for a stratiform cloud in Yan’an area in September 17, 2003 (Northwest China). This cloud dropet data can dispaly the cloud microphysical properties including the droplet number concentration, the cloud water content, the cloud droplet radius, volume radius, effective radius, the cloud droplet relative dispersion, and the prefactor about the ratio of the effective radius and the volume radius. Additionally, using the analytical methods based on the de fi nation of effective radius, we can analytically derive the theoretical parameterization of the cloud droplet effective radius interms of three size distribution funcions described as the Lognormal, the Gamma, and the Weibull expressions, which are usually employed in the numerical models based on the various scales.Results(1) We summarize the Maximum, Mean, Median, and STDEV (Standard Deviation) values about the cloud microphysical properties including the cloud droplet number concentration (Nc), the cloud water content (Qc), the cloud droplet radius (Rm), the volume radius (Rv), the effective radius (Re), the cloud droplet relative dispersion (ε), and theRe/Rvprefactorβfor this stratiform cloud in Yan’an area (Northwest China). (2) Based on the observed data about the cloud droplet number concentrationNcand the cloud droplet relative dispersionε, we can derive aε—Ncnegative relationship asε= 0.579 - 7.42×10-4Nc+ 4.2×10-7Nc2, which represents the cloud droplet relative dispersion decreases with the increase in cloud droplet number concentration. Thisε—Ncrelationship can be directly coupled to the numerical models to evaluated the cloud dropet dispersion effect. (3) We fi nd that theoretical parameterization of the cloud droplet effective radius based on the Lognormal, the Gamma, and the Weibull expressions all fi t better with the observed results, where the parameterization of the Lognormal expression is best for this stratiform cloud in Yan’an area.DiscussionIt is worthy noting that all the observed results is derived from only one case interms of the stratiform cloud in Yan’an area. However, as we know, the macrophysical and microphysical cloud processes are very complex, which is closely related to atmospheric environment (including atmospheric humidity and stability), as well as the aerosol physical and chemical properties. Additionally, various types of clouds have different environment factors, they also have change the cloud droplet effective radius. Hence, we need much more data derived from aircraft measurements including different cloud types, different atmospheric environment, and different aerosol backgrouds to study the paremeterization of the cloud droplet effective radius.ConclusionsCompared with these aircraft measurements of cloud droplet size distributions, it is found that the parameterization of the cloud droplet effective radius based on Lognormal, Gamma, and Weibull expressions all fi t better with the observed results from aircraft measurements, and the parameterization based on Lognormal expression is best for this stratiform cloud in Yan’an area.Recomendations and perspectivesWe recommend that Lognormal expression is the best parameterization of the cloud droplet effective radius for this stratiform cloud in Yan’an area. These results could shed light on understanding the aerosol indirect radiative forcing in Northwest China. Additionally, theε—Ncrelationship has been presented based on this case, which can be coupled to the model to evaluate the cloud droplet dispersion effect.

cloud droplet size distribution; spectral dispersion; cloud droplet effective radius

XIE Xiaoning, E-mail: xnxie@ieecas.cn

10.7515/JEE201601002

2015-11-24；录用日期：2016-01-31

Received Date:2015-11-24;Accepted Date:2016-01-31

国家自然科学基金项目（41105071）；中国科学院战略性先导科技专项（XDA05110101）；国家重点基础研究发展计划项目（2011CB403406）

Foundation Item:National Natural Science Foundation of China (41105071); Strategic Priority Research Program of Chinese Academy of Sciences (XDA05110101); National Basic Research and Development Program of China (2011CB403406)

解小宁，E-mail: xnxie@ieecas.cn