一道竞赛题与其等价式的应用举隅*

●

(双林中学,浙江 湖州 313012)

众所周知，关于三元三次齐次不等式有以下经典试题：

例1已知a,b,c≥0,求证：

(b+c-a)(c+a-b)(a+b-c)≤abc.

(1)

(1983年瑞士数学竞赛题)

展开、整理后，易得其等价式

a3+b3+c3+3abc≥a2(b+c)+b2(c+a)+c2(a+b)=

(2)

a(b2+c2)+b(c2+a2)+c(a2+b2)=

bc(b+c)+ca(c+a)+ab(a+b).

翻阅相关资料后，笔者发现某些不等式问题与之有其惊人的“形似”之处，往往让人有一种“无意插柳”之喜.故而欣然命笔采撷数例，以示“经典试题”在数学竞赛及初数研究中的“特异功能”，以期物尽其用、抛砖引玉.

例2设非负实数a,b,c满足a+b+c=1,求证：

(3)

(2010年全国高中数学联赛广东省预赛试题第3题)

证明在式(1)中，由a+b+c=1,得

(1-2a)(1-2b)(1-2c)≤abc,

即

1-2(a+b+c)+4(bc+ca+ab)-8abc≤abc，

从而

-1+4(bc+ca+ab)≤9abc，

评注在条件a+b+c=1下，式(1)等价于式(3).

类似地，我们可以轻松证明以下赛题：

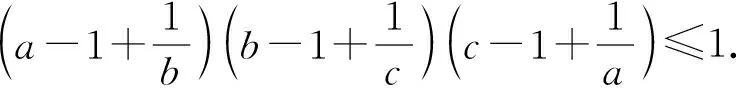
(第41届IMO第2题)

例4已知a,b,c∈R+,且a+b+c=2，证明：

(4)

(《数学通报》2008年6月号问题1 830)

分析1注意到2=a+b+c，从而

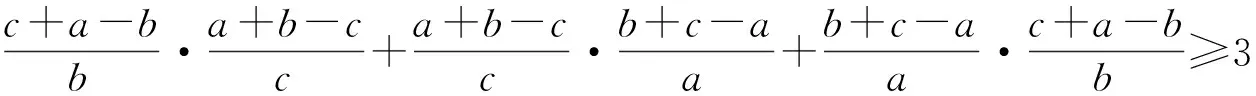
⟺a[a2-(b-c)2]+b[b2-(c-a)2]+c[c2-(a-b)2]≥3abc

⟺[a3-a(b2+c2)+2abc]+[b3-b(c2+a2)+2abc]+[c3-c(a2+b2)+2abc]≥3abc

⟺a3+b3+c3+3abc≥a(b2+c2)+b(c2+a2)+c(a2+b2),

由上式的正确性可知所证式成立.

分析2作代换：(2a,2b,2c)→(a,b,c),可知例4等价于以下不等式问题：

已知a,b,c∈R+,且a+b+c=1.证明：

(5)

易证式(5)⟺式(3)(在a+b+c=1的条件下).因此式(5)成立，从而其等价命题例4得证.

例5若a,b,c>0，则

3(a4+b4+c4)+(bc+ca+ab)2≥6(b2c2+c2a2+a2b2).

(6)

(《数学通报》2017年2月号问题2 350)

分析初看这是一个(三元)四次(齐次)不等式，似乎鞭长莫及、高不可攀，实则是近在咫尺、触手可及的(三元)三次(齐次)不等式问题.

a3+b3+c3+3abc≥a2(b+c)+b2(c+a)+c2(a+b)

⟺(a+b+c)(a3+b3+c3)+3abc(a+b+c)≥(a+b+c)[a2(b+c)+b2(c+a)+c2(a+b)]

⟺a4+b4+c4+a3(b+c)+b3(c+a)+c3(a+b)+3abc(a+b+c)≥a3(b+c)+b3(c+a)+c3(a+b)+

a2(b+c)2+b2(c+a)2+c2(a+b)2

⟺a4+b4+c4+3abc(a+b+c)≥a2(b+c)2+b2(c+a)2+c2(a+b)2

⟺a4+b4+c4+abc(a+b+c)≥2(b2c2+c2a2+a2b2),

(7)

而欲证式其实是3(a4+b4+c4)+2abc(a+b+c)≥5(b2c2+c2a2+a2b2),即

(8)

利用平凡不等式x2+y2+z2≥yz+zx+xy,易知式(7)⟹式(8).故式(6)成立.

评注从例5的分析可以看出，(三元)四次(齐次)不等式(7)与(三元)三次(齐次)不等式(2)等价，且要强于不等式(6)，这是始料未及的.

例6设a,b,c,d>0,且a+b+c+d=4,求证：

(9)

(《数学通报》2017年4月号问题2 356)

分析首先，利用题设a+b+c+d=4,将问题转化为齐次不等式问题：

16(a+b+c+d)(a2+b2+c2+d2)+48(bcd+cda+dab+abc)≥7(a+b+c+d)3,

(10)

其中 (a+b+c+d)(a2+b2+c2+d2)=a3+b3+c3+d3+a(b2+c2+d2)+b(c2+d2+a2)+

c(d2+a2+b2)+d(a2+b2+c2),

(11)

(a+b+c+d)3=a3+b3+c3+d3+3a(b2+c2+d2)+3b(c2+d2+a2)+3c(d2+a2+b2)+

3d(a2+b2+c2)+6(bcd+cda+dab+abc).

(12)

其次，“撇开”三次齐次不等式(10)，自由操作如下：

b3+c3+d3+3bcd≥b(c2+d2)+c(d2+b2)+d(b2+c2),

c3+d3+a3+3cda≥c(d2+a2)+d(a2+c2)+a(c2+d2),

d3+a3+b3+3dab≥d(a2+b2)+a(b2+d2)+b(d2+a2),

a3+b3+c3+3abc≥a(b2+c2)+b(c2+a2)+c(a2+b2),

以上4个式子相加，得

3(a3+b3+c3+d3)+3(bcd+cda+dab+abc)≥ 2[a(b2+c2+d2)+b(c2+d2+a2)+c(d2+a2+b2)]+

d(a2+b2+c2).

(13)

再次，试图利用式(11)和式(12)把式(13)等价变形为式(10)的形式：

式(13)⟺ (3+x)(a3+b3+c3+d3)+(3+x)[a(b2+c2+d2)+b(c2+d2+a2)+c(d2+a2+b2)+

d(a2+b2+c2)]+3(bcd+cda+dab+abc)≥

x(a3+b3+c3+d3)+[2+(3+x)][a(b2+c2+d2)+b(c2+d2+a2)+c(d2+a2+b2)+

d(a2+b2+c2)],

3(bcd+cda+dab+abc)≥

3[a(b2+c2+d2)+b(c2+d2+a2)+c(d2+a2+b2)+d(a2+b2+c2)]+6(bcd+cda+dab+abc)}

上述不等式与式(13)等价，预期目标得以实现.

最后，结合题设a+b+c+d=4,得22(a2+b2+c2+d2)+18(bcd+cda+dab+abc)≥160,即

(14)

而由恒等式(12)及a+b+c+d=4(常数)，知显然有bcd+cda+dab+abc≤4.故而式(9)成立.

评注所得式(14)又强于了所证式(9)，虽是“意料之外”，但着实情理之中.

有关三元不等式的证明题频繁出现于各类各级的数学竞赛和初数研究中，已成为一种“时尚”．要证明它固然不易，但亦有相当的规律可循.依笔者的经验，深入探究三元不等式问题往往需要熟练掌握以下常用的三元代数恒等式与等价不等式：

a(b2+c2)+b(c2+a2)+c(a2+b2)=a2(b+c)+b2(c+a)+c2(a+b)=

bc(b+c)+ca(c+a)+ab(a+b),

a3+b3+c3+a(b2+c2)+b(c2+a2)+c(a2+b2)=(a+b+c)(a2+b2+c2),

a(b2+c2)+b(c2+a2)+c(a2+b2)+3abc=(a+b+c)(bc+ca+ab)，

(b+c)(c+a)(a+b)=(a+b+c)(bc+ca+ab)-abc,

(a+b+c)3=a3+b3+c3+3a(b2+c2)+3b(c2+a2)+3c(a2+b2)+6abc=

a(a2+3b2+3c2+2bc)+b(b2+3c2+3a2+2ca)+c(c2+3a2+3b2+2ab),

(b+c-a)(c+a-b)(a+b-c)≤abc⟺a3+b3+c3+3abc≥a(b2+c2)+b(c2+a2)+c(a2+b2)

⟺a4+b4+c4+abc(a+b+c)≥2(b2c2+c2a2+a2b2).

例1(与其等价式)的最显著功能是帮助我们看出所证三元不等式试题或问题的端倪、走出困境，看到试题或问题的“一线曙光”、找出切入点，或许这些帮助是始料未及的、所得到的结果是更好的……