寻找球心
——四面体外接球问题的关键
☉河南省许昌高中教研处 赵小强
纵观高考题中空间几何体外接球问题,出现最多的就是四面体的外接球问题了.各类问题最终聚焦在球的半径的计算上,但计算半径的前提却都要回答一个问题——球心在哪儿?不同的问题寻找球心的方法也不尽相同,下面我们就一起去看看四面体外接球球心的寻找攻略吧.
一、四面体是正三棱锥
例1 已知正三棱锥P-ABC,PA=a,AB=b,求正三棱锥的外接球的半径R.
解:过P作PH⊥平面ABC,垂足为H,则H是△ABC的重心(中心),则P-ABC的外接球球心O一定在直线PH上.
(1)如图1,当O在线段PH上,连接HC,OC,则OP=OC=R.
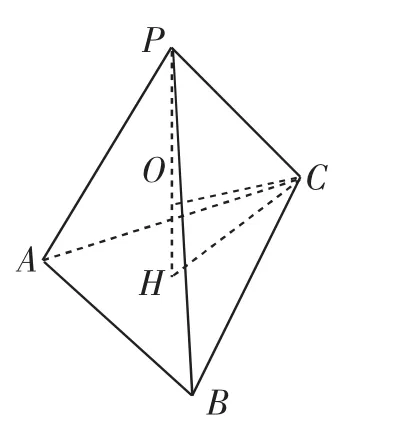
图1



(3)如图2,当O在PH延长线上时,

综上,正三棱锥的外接球半径为

图2
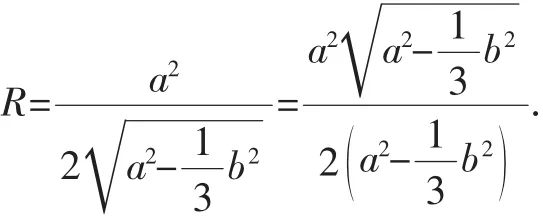
特别地,当a=b时,即四面体PABC为正四面体时,
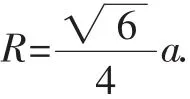
二、四面体是三组对棱分别相等的四面体
例2 已知四面体ABCD中,AB=CD=a,AD=BC=b,AC=BD=c,求四面体ABCD的外接球的半径R.
解:由于三组对棱分别相等,可以考虑把此四面体置入一个长方体中,如图3所示.
则长方体的外接球与四面体的外接球是同一个球(球可以由不共面的四点确定).
设长方体的长、宽、高分别为m,n,p.
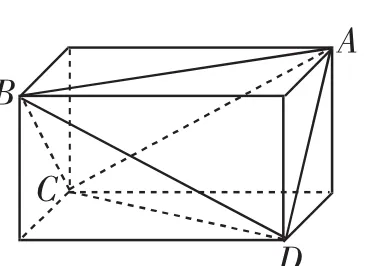
图3
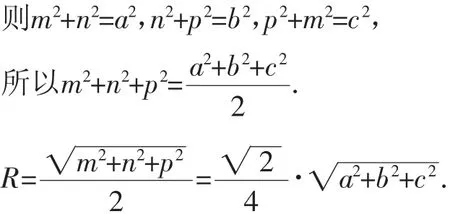
三、四面体含有两个共斜边的直角三角形
例3 已知四面体ABCD,∠BAD=∠BCD=90°,求四面体ABCD的外接球半径R.
解 :在Rt△BAD中,因为∠BAD=90°,Rt△BCD中,∠BCD=90°,所以BD为公共斜边,由直角三角形的性质,BD中点O到A,B,C,D四点距离相等,即O为四面体ABCD的外接球球心,所以
四、四面体存在两个面相互垂直
这种问题又可细分为两种情况,第一种情况为有一条棱垂直于四面体的一个面.第二种情况为仅有两个面垂直,而不存在棱与面垂直.
例4 四面体ABCD,AD⊥平面BCD,AD=a,BC=b,CD=c,BD=d,求其外接球的半径R.
解:由于AD⊥平面BCD,所以把四面体ABCD补成直三棱柱AEF-DBC(如图4),设M,N分别为△AEF,△BCD的外心,则球心O位于MN连线中点,连接OC,NC,构造Rt△ONC,则R=OC,NC为△BCD外接圆半径r.
ON=,在△BCD中运用余弦定理及正弦定理可求出r.

图4

特别地,①当△BCD满足∠BDC=90°时,可得AD,BD,CD两两垂直,于是可把四面体ABCD视为长方体一部分,从而转化为长宽高分别为d,c,a的长方体的外接球问题可得
②当△BCD满足∠BCD=90°或∠DBC=90°时,转化为第三类问题,从而可得
例5 四面体ABCD,平面ABD⊥平面BCD.AB=a,BC=b,CD=c,DA=d,BD=e,求此四面体的外接球半径R.
解:设△BCD的外心为M,△ABD的外心为N,BD的中点为P,根据球的几何性质,球心O必然在过M且垂直于平面BCD的直线与过N且垂直于面ABD的直线交点处.
设△ABD外接圆半径为r1,△BCD半径为r2.
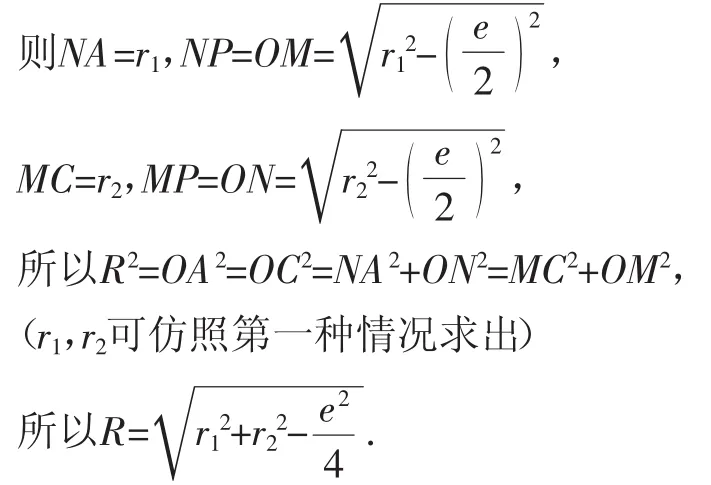
以上,我们列举了几种特殊情形的四面体寻找外接球球心的方法.事实上,任何一个四面体均有外接球,而外接球球心都是在过相邻两面的外心且垂直于相应面的垂线的交点,也都是可以求出的,但由于运算量太大,在命题时缺乏实际价值,我们一般不去考虑.H

