模糊膜计算模型与应用研究综述

彭 宏，王 军

(1.西华大学 计算机与软件工程学院，四川 成都 610039；2.西华大学 电气与电子信息学院，四川 成都 610039)

作为自然计算的一个分支，膜计算(membrane computing)是由欧洲科学院院士乔治伯恩(Gheorghe Păun)于1998年所创立[1]，旨在从生命细胞的结构和功能以及组织、器官和神经系统中抽象出计算模型,这类计算模型称为P系统或者膜系统[2-4].一个P系统通常由4个要素所刻画：膜结构、数据(对象)、操作(规则)以及控制操作的方法.从膜结构来看，有3类P系统：细胞型P系统(cell-like P systems)、组织型P系统(tissue-like P systems)和神经型P系统(neural-like P systems).P系统是一种分布式、并行计算模型.大量研究成果已表明：P系统是通用的(与图灵机等价)，并且也是有效的(能以多项式时间复杂性求解众多的NP难问题)[5-8].

在许多工程问题中，存在各种不确定性的、不准确的信息，其中部分可表现为信息的模糊性.然而，已有的P系统缺乏处理这种不确定性的能力和机制，严重制约了P系统在这些工程问题中的应用.为了突破这个限制，多种模糊P系统已经相继被提出.论文将对这些模糊P系统及其应用的研究现状进行综述，并对未来研究的发展给出几点展望.

1 模糊P系统

模糊P系统(fuzzy P systems)是P系统的一类变体或扩展，它通过在数据和操作等要素中引入模糊集与模糊逻辑所构建.首先回顾模糊脉冲神经P系统，然后介绍模糊组织型P系统.

1.1 模糊脉冲神经P系统

脉冲神经P系统(spiking neural P systems)是一种被广泛讨论的神经型P系统，抽象于神经元沿突触通道发放脉冲现象[9].从结构上看，脉冲神经P系统可视为一个有向图，其中节点为神经元，而有向弧表示神经元之间的突触连接.从内部机理来看，脉冲神经P系统有如下两个要素：

(1) 脉冲数.指神经元中包含的脉冲个数，通常由一个正整数刻画.

(2) 点火规则.点火规则具有E/acap形式，其中E是正则表达式.从应用角度看，它可视为一个点火条件.如果一个神经元所包含的脉冲个数满足anL(E)，则该神经元点火，意味着它的c个被消耗、产生p个新脉冲,并且这些脉冲被传送给其后继的神经元.特别地，如果p=0，则上述规则称为遗忘规则.当遗忘规则被应用时，仅消耗一定的脉冲而不生成新的脉冲.

从上述机理可知，脉冲神经P系统特别适合描述离散事件系统，其中脉冲数表达系统的状态而规则刻画系统的行为.然而，脉冲神经P系统无法用于刻画模糊性.为了突破这个限制，模糊脉冲神经P系统的研究受到极大关注.模糊脉冲神经P系统是脉冲神经P系统的一种扩展或变体.通过引入不同的模糊集和模糊逻辑，多种模糊脉冲神经P系统相继被提出，如模糊推理脉冲神经P系统、加权模糊脉冲神经P系统、自适应模糊脉冲神经P系统、梯形模糊脉冲神经P系统和直觉模糊脉冲神经P系统等.

在文献[10]中，一种模糊推理脉冲神经P系统(fuzzy reasoning spiking neural P systems)被讨论.从内部机理上看，这个扩展主要体现两个方面：(1) [0,1]中的实数作为神经元的脉冲值；(2)采用一种实数型的点火规则，形如aαaβ.原始点火规则中以正则表达式为基础的点火条件被移去，代之以一个简单的点火条件：{α>0}，它表示只要其脉冲值大于0，神经元将点火.另外，max-min模糊逻辑被引入到这个点火规则中实现模糊推理计算.

开发模糊推理脉冲神经P系统的动机之一是用于建模模糊产生式规则和实现动态模糊推理.模糊产生式规则已广泛用于模糊知识表示和推理中，并且也存在多种实现模型，如自适应模糊系统和模糊神经网络.一般地，有3种类型的模糊产生式规则：类型I：IFp1andp2and … andpkTHENpk+1(CF=τ)；类型II：IFp1orp2or … orpkTHENpk+1(CF=τ)；类型III：IFp1THENp2and … andpk+1(CF=τ).其中:p1,p2,…,pk,pk+1为k+1个命题，CF(confidence factor)为模糊规则的置信度因子.为了刻画模糊产生式规则，神经元被进一步划分为两类：命题神经元和规则神经元.命题神经元用于刻画模糊命题，其中神经元的脉冲值为相应命题的隶属度值.规则神经元用于表达一个模糊规则，同时通过其点火规则实现max-min模糊逻辑.神经元的点火机制为模糊产生式规则集的动态模糊推理提供了一条有效途径.另外，模糊推理脉冲神经P系统是一个具有前向结构的系统，其模糊推理本质上是一个前向计算过程.为此，文献[10]开发了一个基于矩阵运算的前向模糊推理算法.由于矩阵运算容易并行实现，所以这个模糊推理算法可在GPU(field-programmable gate array)和FPGA(graphics processing unit)上实现.

为了表达加权模糊产生式规则和处理加权模糊推理，文献[11]提出了一个加权模糊脉冲神经P系统(weighted fuzzy spiking neural P systems).同样，神经元被分成两类：命题神经元和规则神经元.命题神经元定义为一个4元组σp=(α,w,λ,r)，其中：α为脉冲值，w为输出权重向量，λ为阈值，r为点火规则E/aαaα.规则神经元是一个5元组σp=(α,γ,υ,τ,r)，其中：α为脉冲值，γ为确定性因子，υ为输出权重向量，τ为阈值，r为点火规则E/aαaβ.在每个神经元中，采用了阈值型的点火条件：E={α≥λ}或{α≥τ}.

加权模糊脉冲神经P系统用于建模如下加权模糊产生式规则：

类型I：IFp1andp2and … andpkTHENpk+1(CF=τ),w1,w2,…,wk；

类型II：IFp1orp2or … orpkTHENpk+1(CF=τ),w1,w2,…,wk；

类型III：IFp1THENp2and … andpk+1(CF=τ),w.

通过利用神经元的点火机制，该文献开发一种反向推理算法来实现动态模糊推理.该算法包括3个阶段：(1)构建一个直接反向规则关联表；(2)生成一个模糊“⊕-OR”树；(3)模糊真值的计算.

文献[12]讨论了模糊脉冲神经P系统的学习问题，提出了一种自适应模糊脉冲神经P系统(adaptive fuzzy spiking neural P systems).这个自适应系统的核心是一个加权模糊脉冲神经P系统，但是，神经元的输出权重通过学习机制进行调整.该文利用Widrow-Hoff学习率开发了一个模糊脉冲神经P系统的学习算法.

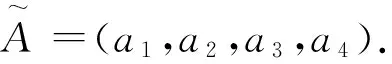
直觉模糊集(intuitionistic fuzzy set)由Atanassov[14]引入.不同于经典的模糊集，一个直觉模糊集A由一个隶属度函数μ(x)和一个非隶属度函数υ(x)刻画，即A={|xX}.特别地，称α=(μα,υα)为一个直觉模糊数.直觉模糊数满足如下运算：(1)α⊕β=(max(μα,μβ),min(υα,υβ));(2)αβ=(μαμβ,υα+υβ-υαυβ);(3)λα=(λμα,λυα).通过引入直觉模糊数，文献[15]提出了一种直觉模糊脉冲神经P系统(intuitionistic fuzzy spiking neural P systems).每个神经元由一个3元组表示，即σ=(α,τ,r)，其中：脉冲值由一个直觉模糊数表示，τ用于刻画规则神经元的置信度，而点火规则r:aαaβ实现相应的模糊逻辑与运算.这个模糊推理机制由一个基于矩阵的前向推理算法实现.推理的结果也是由直觉模糊数表示.由于直觉模糊集由一个隶属度函数和一个非隶属度函数所刻画，所以，对比于基于经典模糊集的模糊脉冲神经P系统，它能更加精细地刻画不确定性.

文献[16]对上述模糊脉冲神经P系统提供了一个统一的形式化.同时，西班牙塞维利亚大学自然计算研究组在膜计算领域著名的仿真平台PLingua中实现了模糊脉冲神经P系统[17].另外，关于模糊脉冲神经P系统的稍早综述可以参见文献[18].

1.2 模糊组织型P系统

组织型P系统是一种具有网状结构的P系统，其中每个细胞视为一个处理器，它处理对象并且沿预先指定的通道传递这些对象.在组织型P系统中，数据为对象(或串)多集，并且通过通信规则实现对象的交流和共享.通信规则有两种类型：(1)双向规则；(2)同向规则.利用对象的多重性，组织型P系统也适合建模离散事件系统.然而，它缺乏处理不确定性的机制.

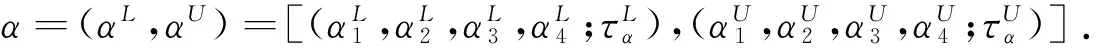
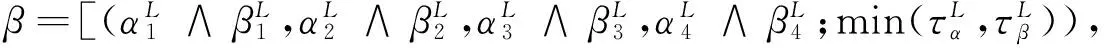
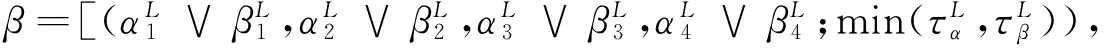
在上述机制的支撑下，模糊组织型P系统可用于刻画不同事件之间的因果关系.

2 模型应用

电力系统是一个国家的重要基础设施，它的可靠和稳定运行对于工业生产和居民生活是极其重要的.一个电力系统由大量的系统元件组成，如发电机、变压器、母线和传输线等.由保护继电器、断路器和一些通信设施组成了电力系统的保护系统.通常，保护系统配置了一个监控与数据采集系统(supervisory control and data acquistion,简称SCADA)，可以依据由SCADA系统所收集的信息进行故障诊断.目前，一些智能计算方法已经用于电力系统的故障诊断，如专家系统[20]、人工神经网络[21]、全局优化技术[22].然而，多种原因会导致由SCADA系统所获得的信息可能是不完整的和非确定性的，特别是复杂故障和在多故障情况下尤为如此.近年，模糊P系统已经被用于讨论电力系统的故障诊断问题.

在文献[10]中，作为一个例子，模糊推理脉冲神经P系统应用于变压器故障诊断，通过建立一个包含18个神经元的故障诊断模型，验证了模糊推理脉冲神经P系统在解决故障诊断问题的有效性.文献[23]讨论了如何应用模糊推理脉冲神经P系统求解电力系统的故障诊断问题.3个电子系统经典例子被分析和讨论，包括一个9总线系统、一个14总线系统和一个IEEE 118总线系统的子网.

文献[13]讨论基于梯形模糊数的模糊脉冲神经P系统的故障诊断模型.为了构建故障诊断模型，3种主要区段(线路、总线和变压器)的模糊产生式规则集被建立，并且给出了3级操作保护设备的置信度等.一个包含28个系统区段、40个断路器和84个保护继电器的经典的电力系统用于说明这种故障诊断模型的有效性，其中分析了两个案例：完整信息和非完整信息情况.另外，包含9语言项的语言值被引入到故障诊断模型中表示梯形模糊数，容易被专家和调度员理解.

文献[24]应用自适应模糊脉冲神经P系统建立电力系统的故障诊断模型.该文的案例研究采用了与文献[13]相同的电力系统例子，并且考虑了3种情况：简单故障情况、多故障情况和非完整信息情况.同时，该文采用最小均方(learning managed system,简称LMS)算法更新诊断模型的权值.在文献[25]中，一种改进的故障诊断模型被讨论，并且采用粒子群优化(part swarm optimization,简称PSO)算法为自适应模糊脉冲神经P系统搜索最优的输出权重.

文献[15]讨论了一种采用直觉模糊脉冲神经P系统的电力系统故障诊断模型.在案例研究中，采用了一个6总线的69 kV的分布式系统和一个345 kV的电力传输系统，并且讨论了4种故障情形：(1)没有失败设备的简单故障；(2)带有断路器误动的复杂故障；(3)带有断路器误动的多故障；(4)带有误动和不正确跳闸信息的多故障.

文献[19]探讨了如何使用模糊组织型P系统求解电力系统的故障诊断问题.不同于模糊脉冲神经P系统，模糊组织型P系统被用于建模一个故障与它的保护设备之间的因果关系.在诊断模型中，模糊语言值用于表达区间值模糊数.一个345 kV的电力传输系统用于说明这个诊断模型的可用性，其中案例研究分析了3种故障情况.

在文献[26]中，模糊推理脉冲神经P系统被用于建立电力机车系统的故障诊断模型.文献[27]使用加权模糊脉冲神经P系统讨论高速铁路牵引供电系统的故障诊断.此外，模糊脉冲神经P系统已经被用于处理入侵检测问题[28-30].除了上述文献外，还有部分未被叙述，如文献[31-35].

3 结束语

膜计算模型与算法是膜计算领域的一个关键科学问题，特别是面向应用问题的算法.这也是开发模糊膜计算模型的主要动机.模糊膜计算模型综合了膜系统和模糊理论两者的优点，为膜计算模型的解决实际应用问题提供了一条有效途径.尽管模糊膜计算模型已成功用于解决诸如电力系统故障诊断等问题，但是应该讲这些工作仍属初步的工作，值得进一步深入研究.作者认为未来的研究方面可以考虑如下几点：

(1) 在模糊集理论中已经提出了多种模糊集和不同的模糊逻辑，并且它们已经用于各种工程应用问题的求解.如何融合更多的模糊集与模糊逻辑开发模糊膜计算模型的新变体是一个进一步研究的方向.

(2) 模糊脉冲神经P系统实现了模糊规则的表达和模糊推理.从功能上看，它相当于自适应模糊系统和模糊神经网络中模糊推理器.所以，如果它的前后端分别加上一个模糊化和去模糊组件，可以构成一个类似于自适应模糊系统和模糊神经网络的模糊推理系统.值得注意的是模糊脉冲神经P系统是一个分布式、并行计算系统.因此.它在信号处理和智能控制问题的应用是一个值得关注的主题.

参考文献：

[4] 张葛祥, 程吉祥, 王涛, 等. 膜计算：理论与应用[M]. 北京： 科学出版社, 2015.

[5] LEPORATI A, MAURI G, ZANDRON C, et al. Uniform solutions to SAT and subset sum by spiking neural P systems[J]. Natural Computing, 2009, 8 (4): 681-702.

[6] ISHDORJ T O, LEPORATI A, PAN L, et al. Deterministic solutions to QSAT and Q3SAT by spiking neural P systems with pre-computed resources[J]. Theoretical Computer Science, 2010, 411: 2345-2358.

[7] SONG T, PAN L. Spiking neural P systems with rules on synapses working in maximum spiking strategy[J]. IEEE Transaction on NanoBioscience, 2015, 14 (4): 465-477.

[8] ZHANG X, PAN L, PUN A. On the universality of axon P systems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26 (11): 2816-2829.

[9] IONESCU M, PUN G, YOKOMORI T. Spiking neural P systems[J]. Fundameta Informaticae, 2006, 71 (2/3): 279-308.

[10] PENG H, WANG J, PÉREZ-JIMÉNEZ M J, et al. Fuzzy reasoning spiking neural P system for fault diagnosis[J]. Information Sciences, 2013, 235: 106-116.

[11] WANG J, SHI P, PENG H, et al. Weighted fuzzy spiking neural P systems[J]. IEEE Transactions on Fuzzy Systems, 2013, 21 (2): 209-220.

[12] WANG J, PENG H. Adaptive fuzzy spiking neural P systems for fuzzy inference and learning[J]. International Journal of Computer Mathematics, 2013, 90 (4): 857-868.

[13] WANG T, ZHANG G, ZHAO J, et al. Diagnosis of electric power systems based on fuzzy reasoning spiking neural P systems[J]. IEEE Transactions on Power Systems, 2015, 30 (3): 1182-1194.

[14] ATANASSOV K. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20 (1): 87-96.

[15] PENG H, WANG J, MING J, et al. Fault diagnosis of power systems using intuitionistic fuzzy spiking neural P systems[J]. IEEE Transaction on Smart Grid, 2017 (1): 267-272.

[16] PÉREZ-JIMÉNEZ M J, GRACIANI C. Fuzzy reasoning spiking neural P systems revisited: a formalization[J]. Theoretical Computer Science, 2017 (1): 4-14.

[18] WANG T, ZHANG G, PÉREZ-JIMÉNEZ M J. Fuzzy membrane computing theory and applications[J]. International Journal of Computers, Communications & Control, 2015, 10 (6): 904-935.

[19] PENG H, WANG J, SHI P, et al. Fault diagnosis of power systems using fuzzy tissue-like P systems[J]. Integrated Computer-Aided Engineering, 2017, 24: 401-411.

[20] CHO H J, PARK J K. An expert system for fault section diagnosis of power systems using fuzzy relations[J]. IEEE Transactions on Power Systems, 1997, 12 (1): 342-348.

[21] CARDOSO G, ROLIM J G, ZÜRN H H. Application of neural network modules to electric power system fault section estimation[J]. IEEE Transactions on Power Delivery, 2004, 19 (3): 1034-1041.

[22] HUANG S J, LIU X Z, SU W F, et al. Application of honey-bee mating optimization algorithm to fault section estimation in power systems[J]. IEEE Transactions on Power Delivery, 2013, 28 (3): 1944-1951.

[23] XIONG G, SHI D, ZHU L, et al. A new approach to fault diagnosis of power systems using fuzzy reasoning spiking neural P systems[J]. Mathematical Problems in Engineering, 2013, 2013 (1): 211-244.

[24] TU M, WANG J, PENG H, et al. Application of adaptive fuzzy spiking neural P systems in fault diagnosis model of power systems[J]. Chinese Journal of Electronics, 2014, 23 (1): 87-92.

[25] WANG J, PENG H, TU M, et al. A fault diagnosis method of power systems based on an improved adaptive fuzzy spiking neural P systems and PSO algorithms[J]. Chinese Journal of Electronics, 2016, 25 (2): 320-327.

[26] WANG T, ZHANG G, PÉREZ-JIMÉNEZ M J. Fault diagnosis models for electric locomotive systems based on fuzzy reasoning spiking neural P systems[C]// Lecture Notes in Computer Science, 2014: 385-395.

[27] WANG T, ZHANG G, PÉREZ-JIMÉNEZ M J, et al. Weighted fuzzy reasoning spiking neural P systems: application to fault diagnosis in traction power supply systems of high-speed railways[J]. Journal of Computational and Theoretical Nanoscience, 2015, 12 (7): 1103-1114.

[28] IDOWU R K, CHANDREN R, OTHMAN Z A. Advocating the use of fuzzy reasoning spiking neural P system in intrusion detection[C]// Asian Conference on Membrane Computing (ACMC), 2014: 1-5.

[29] RUFAI K I. Attack detection in a rule-based system using fuzzy spiking neural P system[J]. International Journal of Informatics and Communication Technology, 2016, 5 (1): 11-20.

[30] IDOWU RK, RAVIE CM, OTHMAN Z A. Denial of service attack detection using trapezoidal fuzzy reasoning spiking neural P system[J]. Journal of Theoretical & Applied Information Technology, 2015, 75 (3): 397-404.

[31] HUANG K, WANG T, HE Y, et al. Temporal fuzzy reasoning spiking neural P systems with real numbers for power system fault diagnosis[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13 (6): 3804-3814.

[32] HUANG K, ZHANG G, WEI X, et al. Fault classification of power transmission lines using fuzzy reasoning spiking neural P systems[C]// Bio-inspired Computing-Theories and Applications, 2017: 109-117.

[33] XIONG G, SHI D, CHEN J. Implementing fuzzy reasoning spiking neural P system for fault diagnosis of power systems[C]// Power & Energy Society General Meeting, 2013: 1-8.

[34] WANG T, ZHANG G, RONG H, et al. Application of fuzzy reasoning spiking neural P systems to fault diagnosis[J]. International Journal of Computers Communications & Control, 2014, 9 (6): 786-799.

[35] WANG J, CHEN K, LI M, et al. Cell-like fuzzy P system and its application in energy management of micro-grid[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13 (6): 3643-3651.