链式膜系统及直接(间接)膜算法与聚类分析研究进展
刘希玉, 姜珍妮, 赵玉祯
(山东师范大学 管理科学与工程学院,山东 济南 250014)
膜计算一词是由欧洲科学院院士、罗马尼亚科学院院士Gheorghe Pǎun[1]在1998年提出,并于2002年将其成果见刊发表.2003年,美国科学情报检索机构(institute for scientific information,简称ISI)将膜计算列为计算机科学中快速发展的前沿领域.此时起,膜计算便成为了一个新兴的研究领域.膜系统主要由膜结构、对象以及进化规则3部分组成,通过模拟细胞、组织或者器官的基本结构而构造的膜结构是计算的主体,规则是实现膜内和膜间物质交流的基础,对象则被置于膜内,依据相应的规则,可完成相应的信息传递过程.
目前为止,膜计算模型主要分为3种:细胞型计算模型、组织型计算模型和神经型计算模型.细胞型计算模型是基于单细胞结构,组织型计算模型基于组织中细胞群结构,神经型计算模型基于神经元细胞.现已被证明,3种模型皆具有图灵等价的计算能力.无论哪种膜系统,其基本计算都是开始于膜系统的某个初始格局,计算随着初始格局的转移而不断进行下去,直至在输出膜中出现计算结果为止.目前基于膜系统提出的近似优化算法是膜计算应用方面一个较热的研究方法,将膜计算与其他传统的优化算法进行结合,可发挥膜系统的优良特性,并借此改善传统算法的不足.
针对膜计算的研究已经层出不穷,但是大部分改进膜系统依然基于图结构的设计,为了充分发挥出膜系统的计算性能,两种新型的膜系统应运而生:(1)在单纯形结构和离散Morse理论基础上构造的单纯形P系统;(2)基于细胞多维框架思想的链式P系统.论文将对两种新型的膜系统进行详细介绍,同时对基于现有膜系统进行的聚类研究进行综述,并对未来相关研究的发展提出几点展望.
1 新型P系统
1.1 单纯形P系统
Liu等[2]基于单纯形的思想结合离散Morse结构提出一种新型的单纯形P系统,并构建了P系统上的交流规则.在该系统中,作者使用了基于网格的聚类方法实现了Wisconsin breast cancer数据集的聚类过程.实验结果表明,新构建的单纯复形P系统(simplicial complexes with membrane coefficients,简称SSP系统)的性能要优于传统的P系统.Xue等[3]提出一种带有膜系数的SSP系统,在复形上扩展了现有的膜结构,并给出了4种基于链式结构和边操作的交流规则.通过模拟寄存器证明了新提出SSP系统的计算完备性,同时将其应用于文档聚类中.通过实验结果进一步证明了新提出的SSP系统较于传统P系统更具聚类优势.
新型的单纯形膜系统的膜结构如图1所示.通过一系列的顶点{a0,a1,…,ak}表示单纯复形K,一个单形σ∈K被称为一个膜,其中单形由顶点表示.如果一个单形不是单纯复形K中其他膜的组成部分,则记该膜为最大膜.顶点是0维膜,称为基本膜.若膜τ<σ是σ的一部分,则记σ是τ的父膜.若两个单形σ1,σ2是同一个更高维单形的组成部分,则称σ1和σ2是邻居关系,记作(σ1,σ2)τ,其中τ表示二者的共同超面,也可以记作(σ1,σ2)L.如果单形τ是两个单形σ1,σ2的一部分,则σ1,σ2是内邻关系,记作(σ1,σ2)τ,也可以记作(σ1,σ2)U或者(σ1,σ2).图1为一个简单的3维单纯形膜系统实例,图2为单纯形膜结构图1的邻居关系.
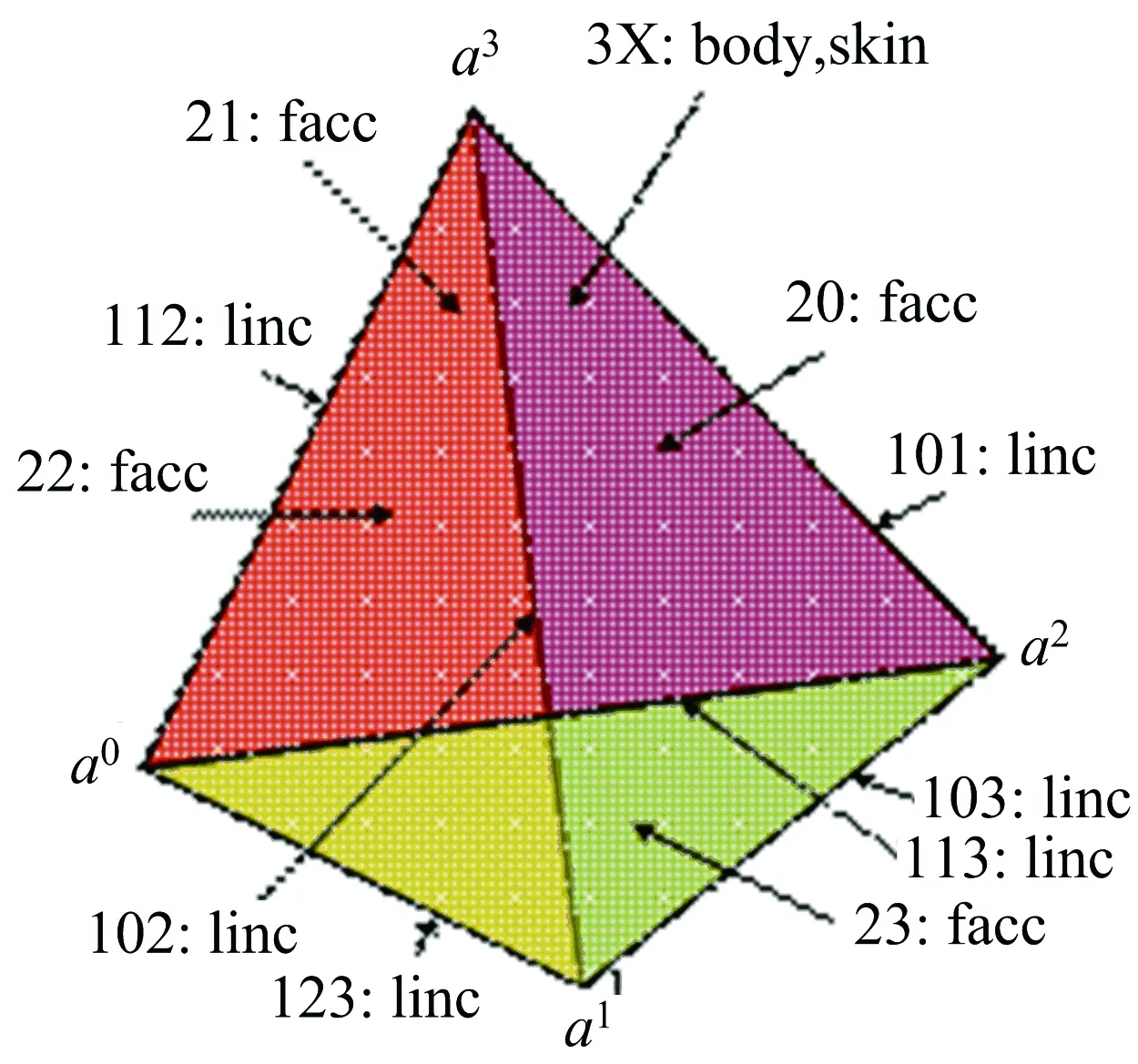
图1 单纯形膜结构

图2 膜结构的网络模型
该膜系统共包含15个膜.单纯形膜系统的膜数量计算方式为
(1)
单纯复形K上表示的系统称为单纯形P系统.带有共运输和逆运输规则的单纯形膜系统定义为
∏=(m,O,E,ω1,…,ωm,R1,…,Rm,ch,F(i,j)|(i,j)∈ch,i0),
其中:o是字母表;m表示细胞的数量标签,标号依次为1,2,…,m;E是环境中的无限制多重集;ωi表示膜i中的初始字符串;Ri表示膜i中的共运输/逆运输规则;ch⊆{(i,j)U,(i,j)L:i,j∈{1,2,…,m}}表示关联集;F(i,j)表示关系(i,j)∈ch上的共运输/逆运输规则;i0表示输出膜.
单纯形P系统中的膜规则,首先明确每个类型的规则都存在out,in,up,down这4种操作.
(1)Rσ(τ1,τ2)中向上关联规则形式为
[(x,y),up;(α,β),in]U→[z,in;γ,down],[u,out;v,in|τ1<σ],[u,out;v,in|τ2<σ],
该规则表示将细胞τ1中的x以及细胞τ2中的y变成z移动到父代σ中,同时将父代σ中的γ分别变成τ1中的α以及细胞τ2中的β.
(2)Rσ(τ1,τ2)中向下关联规则形式为
[(x,y),down;(α,β),in]L→[z,in;γ,up],[u,out;v,in|σ<τ1],[u,out;v,in|σ<τ2],
该规则表示将细胞τ1中的x以及细胞τ2中的y变成z移动到超面σ中,同时将父代σ中的γ分别变成上一层细胞τ1中的α以及上一层细胞τ2中的β.
1.2 链式膜系统
与单纯形P系统的提出一样,同样基于离散Morse结构,栾静等[4]提出一种与离散Morse结构相结合的具有链式结构的新型脉冲神经P系统(spiking neural P system on chain,简称SNPC系统).SNPC系统的神经膜细胞通过离散梯度矢量路径设置链,构建链式结构的SNP(spiking neural P system)系统.作者证明了新提出的SNPC系统在进行自然数运算方面的可行性,并从生成数据集和生成字符串语言的角度给出了SNPC系统中算术运算的算法.Xue等[5]提出了一种结合离散Morse理论的新型定向链式P系统,P系统中的对象以正负两级的形式存在,并证明了该链式P系统具有和图灵机等价的计算能力,将其用于线性时间内对满足性问题的求解,经与其他的P系统对比证明了该链式P系统的有效性.
将链式结构与膜系统进行结合,同样是基于膜对象、膜结构和膜规则3个角度进行.链式膜结构设定如下:(1) 若一个膜内部不再包含其他膜,则该膜为基本膜;(2) 将多个膜相互连接组成一个有序链表,称为链膜;(3) 链膜上的每一个膜为单元膜;(4) 各个基本膜中的符号称为基本对象,链膜中每个单元膜中的基本对象依次连接构成的有序对象称为链对象.链式膜系统可以分为有向链式膜系统和无向链式膜系统,无向链式膜系统是以单纯形多维结构构建的膜系统,各个单元膜之间没有顺序关系.此处仅对有向链式膜系统进行说明.
有向链式膜系统的形式化定义如下
∏=(O,μ,w1,w2,…,wm,R1,R2,…,Rm,io),
其中:O是字母表;μ是膜结构,包括链膜的组成结构以及整个膜系统的组成结构;wi(i=1,2,…,m)为链膜σi中链对象的集合;Ri(i=1,2,…,m)为膜σi内的规则;io是输出膜.
有向链式膜系统中的膜以链膜形式存在,表示为σi=hi1*σi1⊗hi2*σi2⊗…⊗hini*σini,其中:σi1,σi2,…,σini表示该链膜上的单元膜;hi1,hi2,…,hini表示整数;hijσij表示该链膜中包含|hij|个单元膜σij.通过规则控制信息在各单元膜以及各个链膜之间进行交流.有向链式膜系统中,对象以链表形式表示,具体表示为ai=x1⊗x2⊗…⊗xn,代表的含义为单元膜σi中包含单元对象xi.有向链式膜规则表示为ri={ri,1,ri,2,…,ri,n},表示ri是由n个子规则组成,这n个子规则按照从左至右的顺序依次执行.设ai1=gnxn⊗gn-1xn-1⊗…⊗g1x1和ai2=hnxn⊗hn-1xn-1⊗…⊗h1x1是某有向链式膜系统中的任意两个链膜,则链膜相加规则为
ai3=ai1+ai2为ai1+ai2=(gn+hn)xn⊗(gn-1+hn-1)xn-1⊗…⊗(g1+h1)x1,
它也是一个链膜.同样链式膜系统中也可以进行相减、交叉等其他操作.两种链式膜结构形式如图3、4所示.

图3 树形膜结构
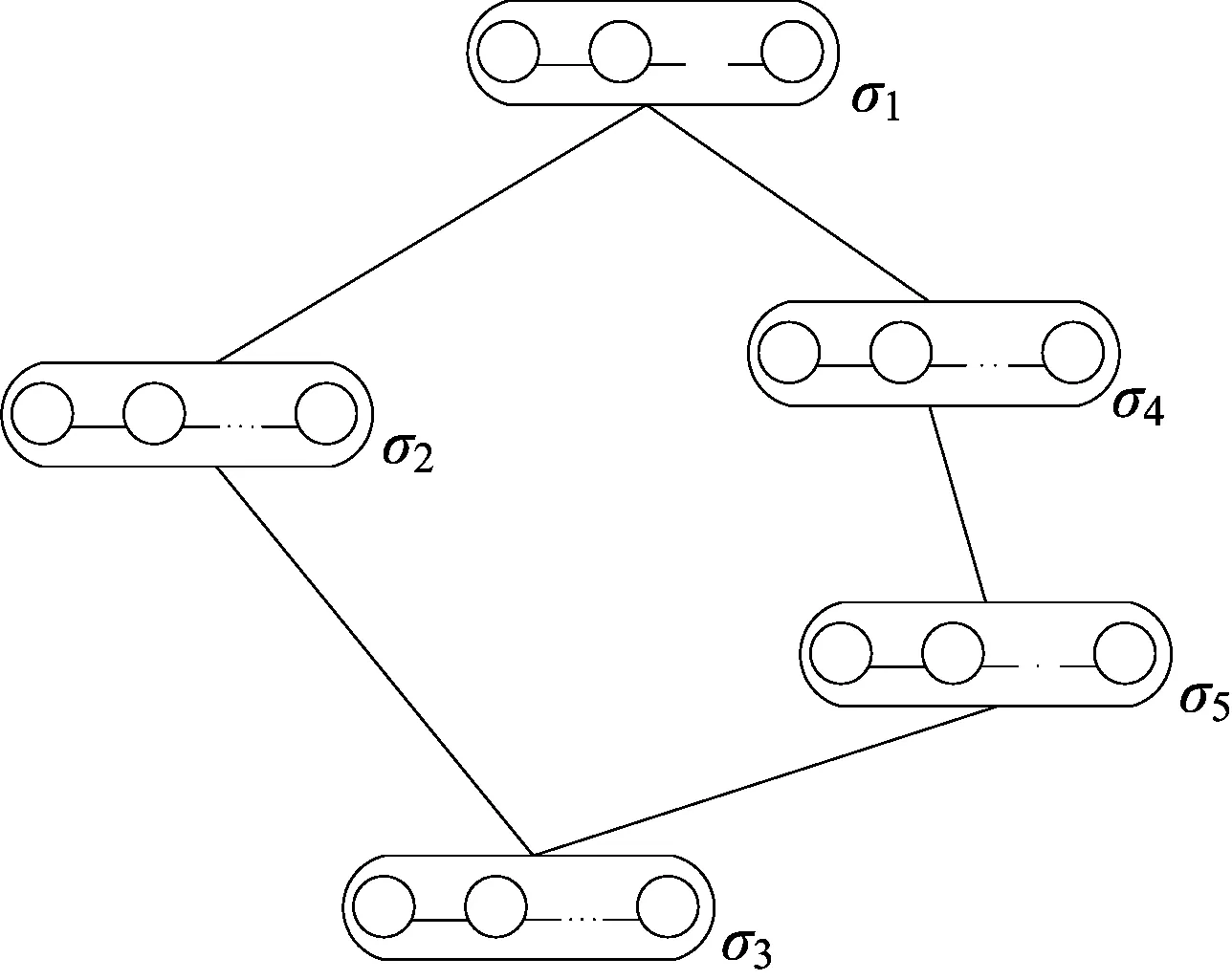
图4 图形膜结构
2 膜计算在聚类问题中的应用
根据膜计算与聚类算法的结合程度可将其分为两个大类:(1)利用直接膜算法求解聚类问题;(2)利用间接膜算法求解聚类问题.直接膜算法是指用P系统的对象表示算法中的数据对象,用P系统的进化规则表示对数据对象操作过程的算法.间接膜算法是将传统的近似算法和膜计算的特性相结合,是一类新的分布式演化算法.此处需要说明关于直接膜算法和间接膜算法两个名词的定义依据的是当前研究现状,并非是一种严格的说法.
聚类分析是数据挖掘中一个非常活跃的研究领域,现已有很多聚类算法.按照聚类思想的不同,可将聚类简单划分为两大类:划分方法和自生长方法.划分方法,即事先确定好类数目,然后按照指定的划分标准将数据集直接生成最终的聚类结果;自生长方法则是从一个数据点出发,按照某种规则,逐步形成一个簇.基于层次的聚类方法和基于密度的聚类算法都属于自生长算法,比较典型的代表包括:BIRCH(balanced iterative reducing and clustering using hierarchies)、CURE(clustering using representatives)、ROCK(robust clustering using links)、Chameleon算法、DBSCAN(density-based spatial clustering of applications with noise)、OPTICS(ordering points to identify the clustering structure)和DENCLUE(density-based clustering)算法等.除了以上几类聚类问题,基于网格的聚类以及基于图论的聚类问题等,也是当前的研究热点.
当前已经存在很多关于膜计算的研究,但是将膜计算应用在聚类分析领域的研究还比较少.将膜计算的极大并行性融入聚类问题分析中,可以有效提高聚类分析的效率,求解大数据下高复杂度、高稀疏性问题,具有一定的应用价值和实践意义.
2.1 基于直接膜算法求解聚类问题
划分方法(partitioning method,简称PAM)的基本思想是首先创建k个划分(即聚类数为k),然后通过一定的预设指标将每个数据点从一个划分转移到另一个划分,从而改善划分的质量.比较典型的划分方法包括:K-means、K-medoids、CLARA(clustering large applications)等方法.目前学者们习惯性地统称该类划分方法为广义K-means聚类.尽管该聚类方法操作简单、高效,但是依然存在很多缺陷,如该方法需要预先指定聚类数目,同时算法采用随机选取初始聚类中心的方法容易使算法陷入局部最优,且由于算法基本思想的限制使得该算法仅适用于球形数据集的聚类.
2012年,有学者开始尝试将膜计算引入聚类问题中[6],借助P系统的极大并行性和较低的计算复杂度特性,有效地提高了聚类的效率.简单的实验运行证明了该思想的可行性,同时也成了膜计算应用层面新的尝试.尽管P系统的引入提高了聚类效率,但是依然无法掩盖聚类算法自身存在的不足,所以在融合P系统进行聚类的同时,引入K近邻思想以及基于数据点密度等优化方法优化K-medoids算法初始聚类中心[7-11],可进一步提高算法的有效性.
与改进聚类算法本身的思想一致,改进P系统的结构也是提高算法计算能力的一种方式.Xu等[12]基于划分聚类中的中心点思想提出一种用于聚类问题的剪接P系统,并使用了10个数据点测试了该P系统的可行性.
集成聚类是一类鲁棒性非常好的聚类方法,它可以根据多个已知的基本聚类划分得出最终的聚类结果.Zhao等[13]在集成聚类中引入了K-medoids算法和带有促进剂和抑制剂的类细胞P系统,提出了一种基于类细胞P系统的K-medoids集成聚类算法.并通过实验证明了所提出的集成聚类算法可以在短时间内获得更高质量的聚类结果.
基于层次的聚类算法分为自上而下和自下而上两种方式.Cardona等[14]将P系统应用到层次聚类中,以矩阵的形式存储数据点之间的相异度,该思路为后期P系统在聚类中的应用提供了思路.Sun等[15]基于该思路对P系统进行简单改进,使用了简单的数据集对论文提出的聚类算法进行了实验验证,最终结果证明了所改进算法的有效性.Zhao等[16]同样也将活性膜P系统应用到分层聚类中.
层次聚类的代表算法主要包括BIRCH、CURE、ROCK、Chameleon算法.Bai等[17-18]将扩展的脉冲神经P系统引入到了层次聚类中.Zhao等[19]构建了基于活性膜P系统的改进ROCK算法,借助于P系统的极大并行性,极大地降低了改进之后聚类算法时间复杂度.Zhao等[20]将类组织P系统应用到凝聚变色龙聚类算法中,实验差错率更低,聚类效果更准确.Zhao等[21]使用基于网格的聚类算法和并行进化机制以及带有促进和抑制因子的分类组织P系统,改进了变色龙算法.
密度聚类则是根据对象之间的密度进行完成聚类,该方式可以发现任意形状的聚类,代表性的密度聚类算法有DBSCAN、OPTICS和DENCLUE算法.Sun等[22]将P系统运用到DBSCAN聚类中.Xue等[23]提出一种基于加权脉冲神经P系统用于求解密度-网格聚类问题.
网格方法可以有效减少算法的计算复杂度,且同样对密度参数敏感.Xue等[24]提出了一种基于网格的带有交流规则的新型P系统,称为格上交流P系统(communication P system on lattice,简称LTC-P).将该系统与基于密度的聚类、基于分层的聚类以及基于划分的聚类进行结合,用于求解聚类问题.聚类过程在膜中实现,聚类结果通过膜输出.最终将新的P系统在UCI(university of californiaIrvine)数据集上进行了实验验证,结果表明该系统比传统算法消耗时间更短,所用规则更少,同时还能提供更简单的膜结构.Xue[25]提出一种基于菱形网格算法和脉冲神经网络P系统的新型算法(combining rhombic grids based algorithm and spiking neural P systems used for solving clustering problems,简称RGSNPS),并将其用于求解聚类问题,最终通过Iris和Wine数据集证明了该混合算法的有效性和准确性.
除了以上聚类方法,基于图论的聚类算法也是当前的研究热点之一.Zhao等[26]直接将聚类问题转化成图论问题,提出了一种基于活性膜P系统的聚类算法.计算时,首先将聚类中的对象转化成图中的顶点,对象之间的相异度表示图的边.Xue等[27]提出一种格上P系统并将其用于求解图聚类问题.Liu等[28]提出一种新的基于图的P系统,该P系统的主要特点就是在图的顶点和边上都存在膜室.两种间隔之间与某些通讯规则是拓扑关联的.为寻找Hopfield神经网络的均衡,论文还提出一种新的神经网络计算技术来求解类分裂问题,通过与传统算法的比较,证明了论文新提出P系统的计算效率.
除此之外,Xue等[29]提出的一种基于树结构的P系统实现空间聚类分析,考虑传统的空间聚类分析都是基于冯·诺依曼计算架构,将直接膜算法运用到聚类问题中,通过给出渠道和规则具体呈现了新的交流P系统.Xiu等[30]提出一种结合了Bin-packing技术的新型P系统,并将其应用于聚类分析中,聚类过程的变异、交换以及能量变换过程均以规则的形式在P系统的膜结构中进行实现,最终将该系统应用于心脏病数据集的聚类中.Xue等[31]提出一种具有上层/下层规则以及同层溶解结构的新型P系统,使用膜规则求解聚类问题,并在UCI的急性炎症信息数据集中进行了实验验证,聚类准确率达到83%.实验结果表示该新型P系统能够准确地对数据集进行聚类.
2.2 基于间接膜算法求解聚类问题
Peng等[32]提出一种具有全局连通结构的类组织膜聚类算法,使用速度-位置作为进化规则,所提出的算法在进化-交流机制下,该膜系统不仅可以获得最佳聚类数目,而且还能非常好地实现聚类划分.Peng等[33]基于前期研究提出了基于类组织P系统求解多目标模糊聚类问题,文中所使用的多目标函数为
(2)
其中:Z1,…,Zk表示需要优化的K个聚类中心;3个目标函数分别表示3种有效性测量指标.
Hou等[34]借助P系统的极大并行性优化量子遗传算法,使用改进之后的算法优化K-means聚类算法的初始聚类中心,克服了K-means算法随机选取聚类中心的不足.改进之后的算法能有效缩短算法的运行时间,并可用于处理大规模数据集以及未知聚类数据数目的数据集.Jiang等[35]提出了一种基于DNA遗传算法和P系统的K-means聚类算法,借助DNA遗传算法的选择、交叉、变异操作实现了初始聚类中心的选择,克服了传统的K-means聚类算法随机选择初始聚类中心的不足,同时借助P系统的极大并行性有效地实现了聚类.
3 结束语
综合目前的研究可以发现,有关膜计算的研究已经存在很多,但是将膜计算应用于聚类分析领域的研究还比较少.膜计算在聚类分析领域是一个新课题,将膜计算的极大并行性与聚类模型进行结合,可以用来处理高复杂度、高数据量的数据集,具有一定的实践意义和应用价值.
膜计算融合其他优化算法进行数据处理的间接膜算法是目前较为热点的研究方向,待求解的问题有:(1)对P系统的进化-交流机制进行改进,使其可以实现自动聚类和多目标聚类;(2)目前研究中的固定膜结构并不可以实现自动聚类,所以未来可研究动态膜结构,并将其用于处理优化问题;(3)尝试构建新型P系统,使其可以用于处理更大规模的数据集;(4)将膜计算用于求解更广范围的聚类问题;(5)目前学者们的研究主要是借用UCI数据集及人工数据集进行实现验证,未来可注重将P系统用于求解实际问题.
参考文献:
[2] LIU X Y, XUE A. Communication P systems on simplicial complexes with applications in cluster analysis[J]. Discrete Dynamics in Nature and Society, 2012, 55 (1): 12-17.
[3] XUE J, LIU X Y. Spiking simplicial P systems with membrane coefficients and applications in document clustering[C]// Lecture Notes in Computer Science, 2016: 158-168.
[4] LUAN J, LIU X Y. A variant of P system with a chain structure[J]. Journal of Information & Computational Science, 2013, 10 (10): 3189-3197.
[5] XUE J, LIU X Y, CHEN P. Communication P System with oriented chain membrane structures and applications in graph clustering[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13 (7): 4198-4210.
[6] ZHAO Y Z, LIU X Y, ZHANG H. The K-medoids clustering algorithm with membrane computing[J]. Indonesian Journal of Electrical Engineering and Computer Science, 2013, 11 (4): 2050-2057.
[7] ZHAO Y Z, LIU X Y, QU J H. The k-medoids clustering algorithm by a class of P system[J]. Journal of International & Computional Science, 2012, 9 (18): 5777-5790.
[8] LI Q, LIU X Y. A K-memoids clustering algorithm with initial centers optimized by a P system[C]// Lecture Notes in Computer Science, 2015: 488-500.
[9] HAN L S, XIANG L S, LIU X Y. The K-medoids algorithm with initial centers optimized based on a P system[J]. Journal of Information & Computational Science, 2014, 11 (6): 1765-1773.
[10] SUN W, XIANG L S, LIU X Y. An improved K-medoids clustering algorithm based on a grid cell graph realized by the P system[C]// Lecture Notes in Computer Science, 2016: 365-374.
[11] SUN W, XIANG L S, LIU X Y. A new P system with hybrid MDE-K-means algorithm for data clustering[J]. Wseas on Computers, 2016, 15: 93-102.
[12] XU J L, LIU X Y, XUE J. Cluster analysis by a class of splicing P systems[C]// Lecture Notes in Electrical Engineering, 2014: 575-581.
[13] ZHAO Y Z, LIU X Y, SUN W X. K-medoids-based consensus clustering based on cell-like P systems with promoters and inhibitors[J]. Communications in Computer and Information Science, 2017, 681: 95-108.
[14] CARDONA M, COLOMER M, ZARAGOZA A. Hierarchical clustering with membrane computing[J]. Computing and Informatics, 2012, 27 (3): 497-513.
[15] SUN J, LIU X Y. Hierarchical clustering with improved P system[C]// Lecture Notes in Computer Science, 2012: 454-460.
[16] ZHAO Y Z, LIU X Y, LI X F. The improved hierarchical clustering algorithm by a P system with active membranes[J]. WSEAS Transactions on Computers, 2013, 12 (2): 8-17.
[17] BAI X, LIU X Y. Hierarchical clustering algorithm by extended SN P systems on friendship building in social networks[J]. Journal of Computational Information Systems, 2013, 9 (12): 4849-4859.
[18] BAI X, LIU X Y. Extended asynchronous SN P systems for solving sentiment clustering of customer reviews in e-commerce websites[J]. WSEAS Transactions on Information Science and Applications, 2013, 10 (6): 195-208.
[19] ZHAO Y Z, LIU X Y, WANG W P. ROCK clustering algorithm based on the P system with active membranes[J]. WSEAS Transactions on Computers, 2014 (13): 289-299.
[20] ZHAO Y Z, LIU X Y, WANG W P. An agglomerate chameleon algorithm based on the tissue-like P system[C]// Communications in Computer and Information Science, 2015, 562: 706-723.
[21] ZHAO Y Z, LIU X Y. A grid-based chameleon algorithm based on the tissue-like P system with promoters and inhibitors[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13 (6): 3652-3658.
[22] SUN J, LIU X Y. The DBSCAN clustering algorithm by a P system with active membranes[J]. WSEAS Transactions on Computers, 2016, 12 (8): 309-319.
[23] MAI S T, HE X, FENG J, et al. Anytime density-based clustering of complex data[J]. Knowledge and Information Systems, 2015, 45 (2): 1-37.
[24] XUE J, LIU X Y. Lattice based communication P systems with applications in cluster analysis[J]. Soft Computing, 2014, 18 (7): 1425-1440.
[25] XUE J, LIU X Y. Rhombic grid based clustering algorithm with spiking neural P systems[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13 (6): 3895-3901.
[26] ZHAO Y Z, LIU X Y, QU J H. Research on the application of the P system with active membranes in clustering[C]// Lecture Notes in Computer Science, 2013: 883-890.
[27] XUE J, LIU X Y. Graph cluster analysis by lattice based P system with conditional rules[C]// Lecture Notes in Computer Science, 2014: 375-377.
[28] XIU X Y, XUE J. A cluster splitting technique by Hopfield networks and P systems on simplices[J]. Neural Processing Letters, 2017: 1-24.
[29] XUE J, LIU X Y. Spatial cluster by communication P system on trees[J]. Journal of Information & Computational Science, 2012, 9 (13): 3883-3893.
[30] LIU X Y, XUE J, XIANG L S. A membrane bin-packing technique for heart disease cluster analysis[C]// Lecture Notes in Electrical Engineering, 2013: 39-49.
[31] XUE J, LIU X Y. Acute inflammations analysis by P system with floor membrane structure[C]// Frontier and Future Development of Information Technology in Medicine and Education, 2014: 281-291.
[32] PENG H, WANG J, PENG S. An automatic clustering algorithm inspired by membrane computing[J]. Pattern Recognition Letters, 2015 (68): 34-40.
[33] PENG H, PENG S, WANG J. Multiobjective fuzzy clustering approach based on tissue-like membrane systems[J]. Knowledge-Based Systems, 2017, 125 (1): 74-82.
[34] HOU C P, LIU X Y. P system based quantum genetic algorithm to solve the problem of clustering[C]// Lecture Notes in Computer Science, 2016: 661-667.
[35] JIANG Z N, ZANG W K, LIU X Y. Research of K-means clustering method based on DNA genetic algorithm and P system[C]// Lecture Notes in Computer Science, 2016: 193-203.

