时间因素对脉冲神经膜系统计算能力的影响

庞善臣，郝少华，宋 弢*，宫法明，潘林强

(1.中国石油大学(华东) 计算机与通信工程学院，山东 青岛 266580；2.华中科技大学 自动化学院，湖北 武汉 430074)

1998年，Păun[1]首次提出了膜计算 (membrane computing)的概念，旨在将细胞中经过亿万年演化沉淀的计算智能抽象成为能够执行计算的模型.膜计算研究的计算模型是分布式并行计算模型，统称为膜系统.膜计算系统结构分类有3类：细胞型膜系统[1]、组织型膜系统[2]、脉冲神经膜系统[3]，其在求解NP(non-deterministic polynomial)问题[4]、聚类分析[5-6]以及关联规则挖掘[7]等问题中均得到了广泛应用.膜计算属于生物启发的计算模型(bio-inspired computing model)[8].该综述评述时间因素对脉冲神经膜系统计算能力的影响.

2006年，受大脑神经元利用激发和脉冲传递进行通讯的生物机理启发，Ionescu等[3]提出了脉冲神经膜系统计算模型.该系统是一类分布式、并行计算模型.第3代神经网络具有以下几个特点：(1)神经元的激发与时间相关联；(2)神经元只有在脉冲数目达到一定程度的时候才激发；(3)利用不同的脉冲编码方式表示系统内的信息.因此，从模型设计的出发点来看，脉冲神经膜系统属于脉冲神经网络的范畴[9].

与传统的人工神经网络不同，脉冲神经膜系统的数据结构为多重集，并且使用形式语言与自动机理论中的文法产生式来描述神经元的激发行为.由于使用文法能够更好地以“语义”的方法描述生物神经元的激发行为，而且文法作为较“底层”的数据结构具有较为丰富的数据处理方式，这些优点使得脉冲神经膜系统展现出良好的计算特性.Siegelmann等[10]在研究人工神经网络的计算能力时发现，人工神经网络实现图灵机的计算能力需要886个“processer”.这一结果被认为是神经网络模型具有解决实际问题能力的理论依据.针对这一问题，Păun等[11]在2007年构造了与图灵机等价的脉冲神经膜系统，并且使用的神经元数目为49个，随后发展出了模块组合优化策略[12]，神经元的数目减少到37个.通过引入神经元容量增加策略，Pan等[13]构建了具有10个神经元的通用脉冲神经膜系统.2016年，这一结果被Song等[14]通过引入request rule，将这一结果进一步改进到4个神经元.与人工神经网络所需的886个“processer”的结果比较，脉冲神经膜系统具有使用较少神经元实现图灵计算能力的良好计算特性.许多学者将脉冲神经膜系统应用到实际问题，如求解组合优化问题[15]、自然语言处理[16]、图形图像处理[17]、电力系统故障诊断[18]、生物信息学[19]等.这使得脉冲神经膜系统迅速成为膜计算研究的热点.欧洲科学院院士Mario J Perez-Jimenez评价脉冲神经膜系统的研究为“膜计算具有活力和前景的分支之一”[15].

生物神经系统中，信息以脉冲发送的时间间隔进行编码，并且在神经元之间进行传递以实现神经元之间的信息交互.神经元之间按照特定时间策略进行信息处理.脉冲神经膜系统中的时间因素主要体现在以下4个方面：

(1) 激发时延.神经元在使用激发规则激发时，产生的脉冲将在一定时间延迟后到达目标神经元.这对应于生物神经元在向临近神经元发送脉冲时，脉冲需要经过突触传递到目标神经元，这一过程所消耗的时间与突触连接的长度密切相关.

(2) 基于时间间隔的信息编码方式.脉冲神经膜系统通过读取脉冲串的方式从环境中读取信息.读取数字时，相邻两个脉冲之间的时间间隔即为读取的数字.系统作为数字集族计算装置时，每次计算终止时，系统内的输出神经元发送至环境的第一个和第二个脉冲的时间间隔定义为系统计算的数字.

(3) 基于全局时钟的神经元协作方式.脉冲神经膜系统中有一个标记计算时刻的全局时钟.在某个时刻下，系统中的神经元将并行地执行信息处理，向临近神经元发送脉冲或者保持缄默.神经元之间相互独立的执行信息处理的工作模式，称为同步工作模式.

(4) 规则执行所消耗时间.在全局时钟标注的时刻下，每条激发规则和遗忘规则的执行和使用都将消耗一个时间单元，称为规则执行时间，这一时间对应于生化反应完成所需要的时长.经典脉冲神经膜系统中将所有规则的执行时间无差别地假设为一个时间单元.

针对上述4个时间因素，人们围绕脉冲神经膜系统展开了研究，发展了若干具有图灵计算能力的脉冲神经膜系统的范式[20-22].采用不同的信息编码方式来编码系统计算的结果，如语言、字符串以及系统读取信息的方式[23-25]，建立了若干神经元不同协作工作模式下的脉冲神经膜系统[26-34]、时间无关脉冲神经膜系统[34]等.通过不同的时间协作策略，脉冲神经膜系统展现出了良好的计算性能，具有图灵通用性.

目前，具有图灵计算能力的脉冲神经膜系统及其变型系统中，几乎都使用了上述的4个时间因素.论文通过分析近十年的研究结果，评述分析时间因素对于脉冲神经膜系统计算能力的影响.通过分析发现，神经元之间的协作是脉冲神经膜系统实现图灵通用计算能力不可获取的因素，而激发时延和基于时间间隔的信息编码方式对于系统的计算能力没有显著的影响.这表明神经元的协同工作策略是该系统解决实际问题时不可或缺的时间因素.

1 脉冲神经膜系统

先给出脉冲神经膜系统的定义，主要介绍激发时延、基于时间间隔的信息编码方式和基于全局时钟的神经元协作方式的定义[3].

一个度为m的脉冲神经膜系统Π定义为如下形式的多元组

Π=(O,σ1,σ2,…,syn,in,out)，

其中：O={a}表示单字母集，字母a被称为脉冲；σ1,σ2,…,σm表示构成系统的m个神经元，神经元σi=(ni,Ri)表示该神经元初始包含ni个脉冲和有限规则集合Ri.

Ri包含两类规则：

(1) 激发规则E/ac→ap;d，其中E表示字母表O上的正则表达式，c≥p>0，d≥0.

(2) 遗忘规则as→λ，其中s≥1.

syn⊆{1,2,…,m}×{1,2,…,m}表示突触集合，且满足(i,i)∉syn，表示没有指向自身神经元的突触.

in,out∈{1,2,…,m}分别表示输入神经元和输出神经元.输入神经元可以从环境中读取信息(编码为脉冲串的形式)，输出神经元可以向环境中发送脉冲.

激发规则使用方式如下：如果某个神经元包含k个脉冲(表示为ak)并且ak∈L(E)(正则表达式E关联的语言集合)，那么激发规则E/ac→ap;d被使用，神经元消耗c个脉冲，向邻接神经元发送出p个脉冲.这p个脉冲经过d步到达目标神经元.参数d被称为激发时延.如果神经元中恰好有s个脉冲，那么通过使用遗忘规则as→λ，这些脉冲将被移出系统.系统中有一个全局时钟，用于为每个神经元标注运行时间.系统开始计算时，记为时刻1，以此类推.系统运行的第t步则表示从时刻t-1到时刻t的时间片段.系统中的神经元在某一时刻t都将并行进行信息处理，即能激发的神经元都将激发，通过激发消耗一定数目的脉冲，并向其临近神经元发送一定数目的脉冲.这一基于全局时钟的神经元之间协作进行信息处理的方式被称为同步工作模式.

脉冲神经膜系统的输入和输出都是以脉冲串的形式编码.对于数字，则是表示为脉冲串的第一个和第二个脉冲的时间间隔.例如，系统读取数字n的方式是神经元读取脉冲串10n-11，其中1表示输入神经元读取1个脉冲的时刻，0表示输入神经元不读取任何脉冲的时刻，两个读取脉冲的时刻间隔恰好为数字n.类似地，系统产生数字n的方式如下：输出神经元在某一时刻t向环境发送1个脉冲，第二次发送脉冲的时刻为t+n.两次发送脉冲的时间间隔为(t+n)-t，表示系统计算/产生数字n.从上述定义不难看出，脉冲神经膜系统的数据结构属于离散的字符多重集，这为脉冲神经膜系统进行自然语言处理提供了很好的支持.

2 时间因素对系统计算能力的影响

分别针对脉冲神经膜系统的4个时间因素：激发时延、基于时间间隔的信息编码策略、基于全局时钟的神经元协作方式、规则执行所消耗时间，分析对系统计算能力的影响.

2.1 激发时延对系统计算能力的影响

激发时延，即参数d，与脉冲神经膜系统的神经元中包含的激发规则相关联，它的设计灵感源于人类大脑神经元中脉冲沿突触传递到目标神经元产生的时间消耗.激发时延在脉冲神经膜系统中的作用是在邻接神经元之间发送脉冲时，调控脉冲到达的时间.

在脉冲神经膜系统提出之后，针对这一时间因素得到了很多计算结果，其中比较有说服力的是脉冲神经膜系统的范式[16]、脉冲神经膜系统[17]的改进范式和脉冲神经膜系统的强范式.对于计算模型范式的研究旨在不减弱计算模型计算能力的前提下，使用较少或者简化的元素.计算模型范式研究是计算机科学研究的经典问题之一.Păun等[16]通过加强神经元之间的协作，提出了脉冲神经膜系统的范式，即在不使用遗忘规则或者激发时延的情况下，证明了脉冲神经膜系统依然具有图灵等价的数字集合的计算和识别能力.通过增加神经元之间的协作，在对脉冲到达的时间不进行任何调控的条件下，实现了具有脉冲“即发即到”特性的图灵等价的脉冲神经膜系统.由此不难看出，激发时延调控系统执行计算的功能，可由系统中神经元之间的协作实现，因此激发时延对于系统的计算能力并不是不可或缺的因素.Garcia等[21]提出了脉冲神经膜系统的强范式，通过进一步增加神经元之间的协作，构造了计算通用的脉冲神经膜系统，而系统中没有任何的激发时延和遗忘规则.虽然该结果使用了较少的元素，但是系统的结构变得异常繁琐，较之使用激发时延和遗忘规则时，复杂程度大大提升.Wang等[18]提出了脉冲神经膜系统的改进范式.通过增加2个神经元的容量(在神经元中包含3n+1和3n+2个脉冲时都可以激发)和扩展激发规则的形式，构造了结构简单且不使用激发时延和遗忘规则的图灵等价的脉冲神经膜系统.该范式是目前已知的、不使用激发时延和遗忘规则的图灵等价脉冲神经膜系统的较简范式.

根据上述结果的分析不难发现，神经元的激发时延对于系统的计算能力并不是一个不可或缺的因素，可以通过增加神经元之间的协作和扩展神经元的容量的方法，在不使用激发时延的情况下构造具有图灵等价计算能力的脉冲神经膜系统.这一结论在很多结果中得到了侧面验证：许多计算通用的脉冲神经膜系统的变型系统的构造中都没有使用激发时延，如带反脉冲的脉冲神经膜系统[30-33]、突触上有激发规则的脉冲神经膜系统[34-37]、带激发权值的脉冲神经膜系统[38]、带星细胞的脉冲神经膜系统[39-40]等.

相关问题：文献[18]中提出的脉冲神经膜系统的范式是否是最简范式，是脉冲神经膜系统的一个公开研究问题.另外，该范式中容量神经元脉冲数目在计算过程中不断增加，直至计算终止.这将造成神经元中脉冲的大量堆砌和冗余.如何在不使用激发时延的前提下，构造结构简单、神经元容量合理增加的图灵等价脉冲神经膜系统的范式也是一个亟待解决的问题.

Chen等[41]针对只包含一条激发规则的神经元，给出了利用神经元级联实现脉冲时延的功能模块，如图1所示.但是，对于多条规则的神经元，如何构建与其等价的无激发时延的模块也是一个未解决的公开问题.

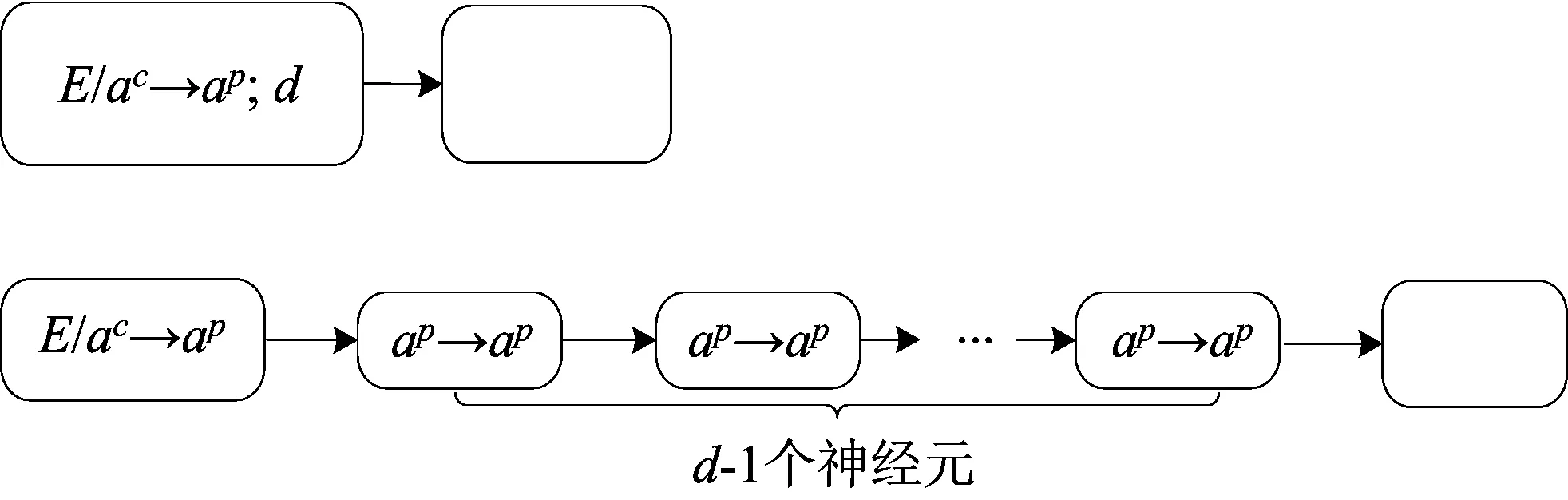
图1 利用神经元级联实现脉冲时延的模块

2.2 基于时间间隔编码方式对系统计算能力影响

在大脑神经系统中，由于信息是以脉冲堆砌的方式编码的，这使得神经元发送脉冲和接受脉冲的时间对于信息的表示具有很重要的影响.例如，当一个神经元处于缄默和积累脉冲的阶段，接受新脉冲的时刻将决定神经元激发的时刻，不同时刻接受不同的脉冲会引起神经元以完全不同的方式激发，从而实现对于不同信息的处理.

受这一生物现实的启发，脉冲神经膜系统以基于时间间隔编码方式通过输入/输出神经元，从环境中读取/向环境发送信息.系统通过读取时间间隔为n的2个脉冲，表示向系统输入数字n；系统以时间间隔n向环境发送2个脉冲，表示系统计算数字n.以这样方式编码输入/输出信息的情况下，Ionescu等[3]证明了脉冲神经膜系统能够计算图灵可计算的数字集族，即具有图灵通用性.

通过改变脉冲神经膜系统读取输入和计算输出的编码策略，该系统可以计算和识别串(string)、语言(language).这方面研究的主要结果包括：Ibarra等[41]提出将脉冲神经膜系统计算的脉冲串直接定义为系统计算的二进制语言、Chen等[41]提出的基于脉冲神经膜系统的字符语言产生和识别方法和轨迹语言产生方法[43]、Wang等[44]提出的基于脉冲神经膜系统的控制语言产生方式等.

Ibarra等[41]提出了将脉冲神经膜系统的计算结果直接定义为其产生的脉冲串，即二进制串：当时刻t输出神经元向外发送1个脉冲，此时将二进制串的第t位记为1；否则记为0.据此可以根据脉冲神经膜系统的计算过程，产生二进制串的集合，称为脉冲神经膜系统产生的二进制语言[39].以这一方式产生语言时，脉冲神经膜系统能够刻画正则语言，其计算能力与有限状态自动机等价，不再具有图灵等价的计算能力.

Chen等[42]提出的基于反转映射策略的产生语言的脉冲神经膜系统.通过对系统生成的二进制串进行反转映射，使每个二进制串对应于某个字母表上的字符串，并且证明了利用这种对应关系，脉冲神经膜系统具有产生递归可枚举语言集族.因此，实现了图灵等价的计算能力.同样，脉冲神经膜系统可以通过反转映射识别任意字母表上的递归可枚举语言.

随后，Chen等[43]又提出了脉冲神经膜系统产生语言的策略——计算过程中特定脉冲的移动轨迹，即计算初始时指定追踪轨迹的脉冲后，将其计算过程中到达的神经元的标记进行连接，形成的字符串构成的集合即为脉冲移动的轨迹语言.且证明了利用这种产生语言的方式，正则语言和递归可枚举语言都可以刻画为脉冲神经膜系统产生轨迹语言的映射语言，即这一产生语言的方式下，脉冲神经膜系统具有与图灵机等价的语言计算能力.

Ramanujan等[44]提出了基于脉冲神经膜系统的控制语言产生方式.在该方法中，每条激发规则都关联一个标签，而将系统从计算开始到终止时，使用的规则标签连接得到的字符串定义为系统产生的控制语言.证明了不使用空标号λ的情况下，脉冲神经膜系统以此方式接受的语言属于上下文有关语言集族；而使用空标号λ的情况，脉冲神经膜系统可以刻画递归可枚举语言，实现了图灵等价性.

根据上述成果分析不难看出，在不使用时间间隔定义系统计算结果的几种情况下，脉冲神经膜系统可以通过利用语言映射等方法实现图灵等价的计算能力.因此，在使用反转映射等辅助策略的条件下，基于时间间隔编码方式对系统计算能力并未有显著的影响.若无其他辅助策略，基于脉冲神经膜系统甚至无法产生很多简单语言[41]，其计算能力有明显的减弱.

相关问题：脉冲神经膜系统作为语言产生和识别装置在理论上具有与图灵机等价的计算能力，但是如何将这些理论研究成果转化用于解决实际问题，是脉冲神经膜系统研究中的重要研究方向之一.具体来看，如何将脉冲神经膜系统应用于自然语言处理，包括语言/语音识别、机器翻译、图语言识别等，都是值得深入研究的课题.

2.3 神经元协作方式对系统计算能力影响

脉冲神经膜系统中有一个假设的全局时钟，它的作用是对每个神经元的时间进行标注，将系统执行计算的时间划分成若干时间单元，标注为有限时间时刻，分别标记为1,2,…,t,…,n,….经典的脉冲神经膜系统中，系统中的所有神经元在任意时刻t都各自并行执行信息处理和脉冲的传递，从而实现神经元之间的协作.这一方式也被称为基于全局时钟的神经元的同步协作方式.同步协作工作模式下的脉冲神经膜系统具有图灵通用性，即能够计算/识别图灵可计算的数字集合[3].随后，人们开始研究不同工作模式下脉冲神经膜系统的计算特性，包括异步工作模式[30]、局部同步工作模式[31]、有限异步工作模式[32].

异步工作模式下，使用扩展激发规则(神经元的每次激发可以向其邻近神经元发送多个脉冲)的脉冲神经膜系统具有图灵机等价的数字计算能力和语言产生/识别能力.但是，使用标准激发规则时，异步工作模式下的脉冲神经膜系统的计算能力是一个尚未解决的公开问题.值得一提的是，同步工作模式下的脉冲神经膜系统的计算能力是与图灵机等价的[30].

Chen等[41]提出了限制的异步工作模式下的脉冲神经膜系统.该系统中，神经元被限制在一定的时间内以异步的方式执行，一旦超出时限，神经元将以同步的方式执行信息处理.这一具有限制的异步工作模式的脉冲神经膜系统，在使用标准激发规则时具有图灵等价的计算能力.

Song等[27]提出了带有局部同步神经元集合的异步工作模式下的脉冲神经膜系统.在这类系统中，系统中存在多个神经元同步集合，而属于同一个同步集合的神经元在同步工作模式下进行信息处理.其他神经元均以异步工作模式进行信息处理.局部同步工作模式下，使用标准激发规则的脉冲神经膜系统具有图灵机等价的计算能力.根据上述分析不难看出，若使用扩展激发规则，即允许神经元发送多个脉冲，异步工作模式下的脉冲神经膜系统具有图灵机等价的计算能力.若限制神经元每次激发只能发送1个脉冲，通过增加局部同步集合和激发时延可以实现图灵机等价的计算能力.由此可得结论，随着神经元发送脉冲数目能力的增加，异步工作模式下的脉冲神经膜系统的计算能力不会减弱，即具有图灵通用性.使用标准激发规则的异步工作模式下的脉冲神经膜系统的计算能力是一个亟待解决的公开问题.Song等[31]提出一个猜想，局部同步集合中至多需要2个神经元，局部同步脉冲神经膜系统就可以实现图灵通用性.这一猜想的数学证明也是尚未解决的公开问题.

2.4 规则执行所消耗时间对系统计算能力的影响

脉冲神经膜系统中有一个全局时钟，其功能是标注系统中每一个神经元的运行时间.系统中定义神经元执行规则的时间消耗为一个时间单元，即规则在时刻t开始执行，那么其使用将在时刻t+1结束.这一过程对应于生物过程中产生脉冲所执行生化反应的时间消耗.

2010年，Pan等[39]通过在系统中引入规则集合的时间映射e:R→N，用来标注规则集合R中的每条规则的执行时间.为了研究规则执行时间对脉冲神经膜系统计算能力的影响，Pan等[46]证明了对于任意的时间映射R(称为时间无关)，脉冲神经膜系统在使用扩展激发规则的情况下，具有与图灵机等价的计算能力，并且构造了由10个神经元构成的计算通用的脉冲神经膜系统.这一结果说明，规则的执行时间对于脉冲神经膜系统的计算能力没有显著影响.

相关问题：对于任意的时间映射R，脉冲神经膜系统在使用标准激发规则的情况下，是否具有图灵等价的计算能力是尚未解决的公开问题.另外，时间无关脉冲神经膜系统产生/识别语言的能力尚未可知.

3 结束语

分析评述了脉冲神经膜系统中时间因素对其计算能力的影响，通过分析比较不同时间因素下脉冲神经膜系统计算能力的结果表明：神经元的激发时延对于系统的计算能力并不是一个不可或缺的因素，可以通过增加神经元之间的协作和扩展神经元容量的方法实现系统的图灵等价计算能力.通过使用反转映射等辅助策略，基于时间间隔编码信息的方式对系统计算能力并未有显著的影响；若无其他辅助策略，其计算能力有明显的减弱.通过增加神经元发送脉冲数目能力，异步工作模式下的脉冲神经膜系统的计算能力不会减弱，即具有图灵通用性.而使用标准规则时，系统的计算能力尚属公开问题.规则的执行时间对于脉冲神经膜系统的计算能力没有显著影响.

有关时间因素对于脉冲神经膜系统计算能力的影响公开问题在每一部分中进行了介绍.这里讨论一下脉冲神经膜系统中的时间因素在系统应用中的影响.模糊脉冲神经膜系统被证明是故障诊断系统建模分析的有效工具[45-47].如何结合脉冲神经膜系统中对系统计算能力没有显著影响的时间因素，对多发系统、多时间尺度系统等复杂系统进行建模分析是一个具有前景的研究方向.

小通用系统研究是计算机科学领域中的经典问题，旨在使用较少的计算资源达到客观的计算能力.脉冲神经膜系统具有良好的计算性能，即具有与图灵机等价的数字计算、数字识别、函数计算、语言产生和识别的能力.如何使用较少的计算资源(这里计算资源可以是神经元数目、神经元种类、规则种类和数目、突触数目等)实现客观的计算能力是一个值得深入研究的方向.

脉冲神经膜系统是离散的计算模型，其数据结构是字符多重集，信息处理方式是基于形式语言的“规则”，这为基于脉冲神经膜系统进行自然语言处理包括语言识别和语言产生等，提供了很好的天然特性，是脉冲神经膜系统未来研究中具有活力的研究分支.

近年来，随着信息化程度的不断加深，信息科学迎来了大数据时代.深度学习是大数据处理中的关键技术.如何在脉冲神经膜系统的框架下发展学习方法，是脉冲神经膜系统探究的热点问题.在脉冲神经膜系统的框架下发展深度学习的方法，是系统在实际应用中的重要研究课题.

参考文献：

[2] MARTIN-VIDE C, PUN G, PAZOS J, et al. Tissue P systems[J]. Theoretical Computer Science, 2003, 296 (2): 295-326.

[3] IONESCU M, PUN G, YOKOMORI T. Spiking neural P systems[J]. Fundamenta Informaticae, 2006, 71 (2/3): 279-308.

[4] ZHAO Y, LIU X, WANG W. Spiking neural P systems with neuron division and dissolution[J]. PloS One, 2016, 11 (9): 262-282.

[5] LIU X, XUE J. A cluster splitting technique by hopfield networks and P systems on simplices[J]. Neural Processing Letters, 2017 (5): 1-24.

[6] LIU X, XUE A. Communication P systems on simplicial complexes with applications in cluster analysis[J]. Discrete Dynamics in Nature and Society, 2012, 16 (3): 4-17.

[7] LIU X, ZHAO Y, SUN M. An improved apriori algorithm based on an evolution-communication tissue-like P system with promoters and inhibitors[J]. Discrete Dynamics in Nature and Society, 2017 (1): 1-11.

[8] ZHANG G, PAN L. A new branch in natural computing-membrane computing[J]. Chinese Journal of Computers, 2010, 33 (2): 208-214 (in Chinese).

[9] MAASS W. Networks of spiking neurons: the third generation of neural network models[J]. Neural Networks, 1997, 10 (9): 1659-1671.

[10] SIEGELMANN H T, SONTAG E D. On the computational power of neural nets[J]. Journal of Computer and System Sciences, 1995, 50 (1): 132-150.

[12] ZHANG X, ZENG X, PAN L. Smaller universal spiking neural P systems[J]. Fundamenta Informaticae, 2008, 87 (1): 117-136.

[13] PAN L, ZENG X. A note on small universal spiking neural P systems[C]//Workshop on Membrane Computing， 2009: 436-447.

[14] SONG T, PAN L. Spiking neural P systems with request rules[J]. Neurocomputing, 2016, 193: 193-200.

[15] ZHANG G, RONG H, NERI F, et al. An optimization spiking neural P system for approximately solving combinatorial optimization problems[J]. International Journal of Neural Systems, 2014, 24 (5): 144-146.

[17] DIAZ-PERNIL D, PENA-CANTILLANA F, GUTIERREZ-NARANJO M A. A parallel algorithm for skeletonizing images by using spiking neural P systems[J]. Neurocomputing, 2013, 115: 81-91.

[18] WANG T, ZHANG G, ZHAO J, et al. Fault diagnosis of electric power systems based on fuzzy reasoning spiking neural P systems[J]. IEEE Transactions on Power Systems, 2015, 30 (3): 1182-1194.

[19] CHEN Z, ZHANG P, WANG X, et al. A computational approach for nuclear export signals identification using spiking neural P systems[J]. Neural Computing and Applications, 2016 (5): 1-11.

[20] IBARRA O H, PUN A, PUN G, et al. Normal forms for spiking neural P systems[J]. Theoretical Computer Science, 2007, 372 (2/3): 196-217.

[21] GARCIA A M, PEREZ D, RODRIGUEZ-P A, et al. Spiking neural P systems: stronger normal forms[J]. Proceedings of the Fifth Brainstorming Week on Membrane Computing, 2007, 5 (5):411-425.

[23] ZHANG X, ZENG X, PAN L. On languages generated by asynchronous spiking neural P systems[J]. Theoretical Computer Science, 2009, 410 (26): 2478-2488.

[24] CHEN H, FREUND R, IONESCU M, et al. On string languages generated by spiking neural P systems[J]. Fundamenta Informaticae, 2007, 75 (3/4): 141-162.

[25] NISHIDA T Y. Computing k-block morphisms by spiking neural P systems[J]. Fundamenta Informaticae, 2011, 111 (4): 453-464.

[26] SONG T, PAN L. Spiking neural P systems with rules on synapses working in maximum spikes consumption strategy[J]. IEEE Transactions on NanoBioscience, 2015, 14 (1): 38-44.

[27] SONG T, PAN L. Spiking neural P systems with rules on synapses working in maximum spiking strategy[J]. IEEE Transactions on NanoBioscience, 2015, 14 (4): 465-477.

[28] IBARRA O H, PUN A, RODRIGUEZ-PATON A. Sequential SNP systems based on min/max spike number[J]. Theoretical Computer Science, 2009, 410 (30/31/32): 2982-2991.

[29] SONG T, PAN L, JIANG K, et al. Normal forms for some classes of sequential spiking neural P systems[J]. IEEE Transactions on NanoBioscience, 2013, 12 (3): 255-264.

[30] CAVALIERE M, IBARRA O H, PUN G, et al. Asynchronous spiking neural P systems[J]. Theoretical Computer Science, 2009, 410 (24/25): 2352-2364.

[31] SONG T, PAN L, PUN G. Asynchronous spiking neural P systems with local synchronization[J]. Information Sciences, 2013, 219: 197-207.

[32] WANG X, SONG T, GONG F, et al. On the computational power of spiking neural P systems with self-organization[J]. Scientific Reports, 2016, 6: 27624.

[33] PAN L, ZHANG X, ZENG X, et al. A survey to spiking neural P system[J]. Chinese Journal of Computers, 2008, 12: 2090-2096 (in Chinese).

[34] PAN L, ZENG X, ZHANG X. Time-free spiking neural P systems[J]. Neural Computation, 2011, 23 (5): 1320-1342.

[36] SONG T, WANG X, ZHANG Z, et al. Homogenous spiking neural P systems with anti-spikes[J]. Neural Computing and Applications, 2014, 24 (7/8): 1833-1841.

[37] METTA V P, KELEMENOVA A. Universality of spiking neural p systems with anti-spikes[C]//TAMC, 2014: 352-365.

[38] SONG T, XU J, PAN L. On the universality and non-universality of spiking neural P systems with rules on synapses[J]. IEEE Transactions on NanoBioscience, 2015, 14 (8): 960-966.

[39] PAN L, WANG J, HOOGEBOOM H J. Spiking neural P systems with astrocytes[J]. Neural Computation, 2012, 24 (3): 805-825.

[40] MACIAS-RAMOS L F, PEREZ-JIMENEZ M J. Spiking neural P systems with functional astrocytes[C]//International Conference on Membrane Computing, 2012: 228-242.

[41] IBARRA O H, WOODWORTH S. Characterizing regular languages by spiking neural P systems[J]. International Journal of Foundations of Computer Science, 2007, 18 (6): 1247-1256.

[42] CHEN H, IONESCU M, ISHDORJ T O, et al. Spiking neural P systems with extended rules: universality and languages[J]. Natural Computing, 2008, 7 (2): 147-166.

[43] CHEN H, IONESCU M, PUN A, et al. On trace languages generated by (small) spiking neural P systems[C]// International Workshop on Descriptional Complexity of Formal Systems - Dcfs, 2006: 94-105.

[44] RAMANUJAN A, KRITHIVASAN K. Control languages associated with spiking neural P systems[J]. Romanian Journal of Information Science and Technology, 2012, 15 (4): 301-318.

[45] PAN L, WANG J, HOOGEBOOM H J. Limited asynchronous spiking neural P systems[J]. Fundamenta Informaticae, 2011, 110 (3/4): 271-293.

[46] SONG T, PAN L, JIANG K, et al. Normal forms for some classes of sequential spiking neural P systems[J]. IEEE Trans NanoBioscience, 2013, 12 (3): 255-264.

[47] WANG J, SHI P, PENG H, et al. Weighted fuzzy spiking neural P systems[J]. IEEE Transactions on Fuzzy Systems, 2013, 21 (2): 209-220.