基于数学建模核心素养的教学设计*—以“公切线”一课为例

广东省广州市第十六中学(510080) 温伙其

笔者有幸参加广州市越秀区“一师一优课,一课一名师”活动,选择怎样的教育理念构建《公切线》这一节课?课堂教学应该呈现什么?笔者一直在思考.结合我国新一轮课程标准修订工作的如火如荼的开展,“核心素养”成为教育理论、教育实践和教育研究的重要议题.基于这样的背景,笔者选择以怎样形成“核心素养”中的数学建模为主线,进行设计,现成文如下:

一.教材学情分析

本节教学内容,教材安排在选修系列一《导数及其应用》的第3节:导数的几何意义.对切线的认知,学生在初中平面几何中圆已初步获得:直线与圆有唯一公共点时,这时直线叫做圆的切线.而圆是一种特殊曲线,这种定义不适用于一般曲线的切线.高中教材,通过逼近方法,将割线趋于的确定位置的直线定义为切线,这种定义方法,适用于各种曲线的切线,使切线的内涵进一步发展,切线的本质得到了直观[1].教材没有进一步探讨两曲线的的公切线,而近年不论全国高考和还是各地高考试题都大量涉及公切线的解题应用,基于此知识背景,学生对切线问题熟悉,对公切线知识空白陌生.

二.教学目标分析

1.知识与能力

(1)会用直线模型求曲线的切线方程;(2)会用直线斜截式模型求两曲线的公切线方程;(3)会用方程模型判断两曲线公切线的数量.

2.过程与方法

通过引入,让学生准确区分切线方程有“在点P处的切线”和“过点P处的切线”两种;借助两个例题,使学生建立公切线分共切点和不同切点两种情况知识体系;拓展延伸,最终引导学生探讨公切线条数,把数量问题转化为函数的的零点.过程由浅如深,逐步递进,环环体现着转化与化归、数形结合和特殊到一般的数学思想.

3.情感与态度

通过本节课学习,学生经历“求切线方程”→“求公切线方程”→“用公切线解决零点、不等式问题”解题过程,体验数学知识的产生是水到渠成的,从而养成勇于探索新知的情感态度.

三.教学重点与难点分析

教学重点:从切线方程中抽象归纳公切线模型(数学抽象、数学建模).

教学难点:公切线的斜率、截距相等方程组推理构造函数,进而判断公切线数量(逻辑推理、数学运算).

四.教学过程

数学模型一直线方程y-y0=k(x-x0)模型解决切线问题

新课引入

2.过点Q(2,0)且与曲线相切的直线方程为___.

设计立意通过自主学习,掌握导数的几何意义即为过此切点切线的斜率;能准确区分“在点P(x0,y0)处的切线”和“过点Q(x0,y0)处的切线”:即前者P(x0,y0)为切点,而后者Q(x0,y0)不一定为切点,为后续公切线的探讨奠定基础.

借助几何画板动态演示切线图形,使学生从感官和数学关系二维角度认识切线,让学生自主完成小结1:

小结1.曲线切线类型和求解流程图:

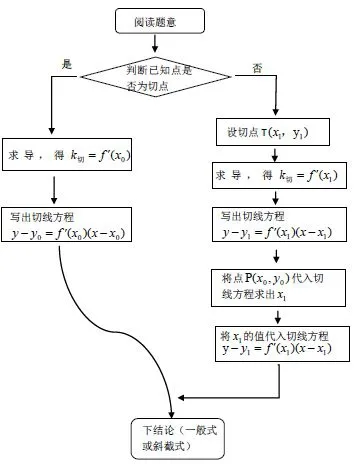
例题讲解

数学模型二方程组模型解决共切点公切线问题

例1(2013年新课标I理科第21题改编)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.求a,b,c,d的值.

解f′(x)=2x+a,g′(x)=ex(cx+d+c),由题意有

变式1(2010年陕西文科第21题改编)已知函数若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值和该切线方程.

数学模型三直线斜截式方程中表示同一直线模型解决公切线问题

例2(2015年新课标II文科第16题)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,求a的值.

解由y=x+lnx的导数又因为切点P(1,1),所以切线斜率所以切线方程为y-1=2(x-1),即y=2x-1.由y=ax2+(a+2)x+1,得y′=2ax+a+2.设切点所以切线斜率所以切线方程为即所以解得,故答案为:8.

变式2(2016年新课标II理科第16题)若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,求b的值.

设计立意通过两道例题的教学,让学生意识切线问题还可深入研究两曲线的公切线,建立公切线包含共切点和公切线不共切点两种情况知识体系.进一步探讨得到规律:共切点的公切线,其特点为相同切点,相同切线,即满足方程组;不共切点的公切线的处理办法,回归曲线过点切线方程的求解过程,分别求出切线l1∶y=k1x+b1、l2∶y=k2x+b2,则有斜率截距分别相等此等量关系,即满足方程组

借助几何画板动态生成变式1,例题2公切线图形,为学生提供直观感性的材料,帮助学生从抽象到具体,归纳出两类公切线的性质,自主完成小结2.

小结2.公切线类型及求解过程步骤:

共切点公切线不同切点公切线特点相同切点,相同切线不同切点,相同切线求解过程步骤第一步:设f(x)与g(x)的公共点为P(x0,y0);第二步:根据公共点及公共切线得到方程组f(x0)=g(x0)f ′(x0)=g′(x0);1.在曲线C1上设切点P(x1,f(x1)),求出过点P切线l1∶y=k1x+b1;2.在曲线C2上设切点Q(x2,f(x2)),求出过点Q切线l2∶y=k2x+b2;3.因为l1,l2表示同一直线,所以斜率截距分别相等,则有方程组第三步:对上述方程组消元求解.k1=k2 b1=b2进行消元求值.

拓展延伸

数学模型四方程f(x)=0模型判断公切线数量问题

1.若一条直线同时和两个曲线相切我们称此直线为两曲线的公切线,已知f(x)=x2,g(x)=-x2+2x+a.

(1)若f(x)与g(x)只有一条公切线,求实数a值;

(2)若f(x)与g(x)有两条公切线,求实数a的取值范围.

解f(x)=x2的导数为的导数为g′(x)=-2x+2,设f(x)=x2上切点可得切线方程为同理设g(x)=-x2+2x+a上切点则切线方程为即两函数有公切线,即令上述两切线方程相同,则有消去x1,化为可得取得最大值

(1)若f(x)与g(x)只有一条公切线,即有关于x0的方程有且只有两个相等的实根,可得

(2)若满足存在两条不同公切线,只需关于x0的方程有两个不等的实根,可得

设计立意进一步理解由公切线的定义可得斜率相等且纵截距相等,消元整理可得新方程;上述所得方程,化归转化为函数,把公切线问题转化为函数零点问题,通过求导判断函数单调性极值,借助图象特点,可以判断零点个数(即公切线的数量),也可证明不等式.

六.布置作业

1.(2009年江西理科第12题)若存在过点(1,0)的直线与曲线都相切,则a等于()

2.已知函数f(x)=blnx,g(x)=ax2-x(a∈R).

(I)若曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,求实数a、b的值;

(II)当b=1时,若曲线f(x)与g(x)在公共点P处有相同的切线,求证:点P唯一;

(III)若a＞0,b=1,且曲线f(x)与g(x)总存在公切线,求正实数a的最小值.

设计意图以两道高考真题作为本节课的课后作业,让学生课后独立完成,一是再次体验导数的几何意义切线斜率的应用,深化公切线中方程组思想,领悟和函数结合过程,解决最值、零点和不等式问题,二是把握考试命题规律,三是检验学生对课堂内容的掌握程度.

本节课以“公切线”为主题,探究导数几何意义作为工具构建公切线的基本办法,教学过程处处渗透“数学建模”素养的培养:(1)在点的切线;(2)过点的切线;(3)在公共点的公切线:(4)不同切点的公切线;(5)切线数量问题转化为方程问题.总而言之,最新一轮课改精神学科核心素养的落实,应在数学课堂中不断的探索,实践和创新.

[1]人民教育出版社、课程教材研究所著.数学选修1-1教师教学用书[M].北京:人民教育出版社,2016.6.