一种优化的单电阻电流采样矢量控制算法研究

马 凯，胡 博，吴俊鹏

(1.中国矿业大学，徐州 221116；2.国网河南省电力公司郑州供电公司，郑州 450000)

0 引 言

在高性能的交流调速系统中，为了有效地控制电机的电磁转矩，获取精准的三相定子电流来构成闭环控制十分必要。定子电流的检测是否精准将直接影响电机控制的效果。使用霍尔电流传感器固然方便，但是在一些成本低、体积小的应用场合，电流传感器不适用。

近年来，许多研究都着眼于采集直流母线电流来重构出三相相电流。这种方法可以明显地减少传感器的数量，有效地降低成本，减小系统体积，还可以消除由输出端电流传感器的不等增益引起的负载不平衡。依据逆变器在不同开关状态下直流母线电流与相电流的关系，在正确的时刻提取出直流母线电流，就可以有效地提取出两相的相电流[1-5]。

有效开关状态的持续时间可能非常短，以至于直流母线电流不能够被有效地采样到。为了确保采样到准确且有效的电流信号，电流采样需要满足最小采样时窗Tmin的要求，Tmin：

Tmin=Td+Tset+Tsam

(1)

式中：Td为死区时间；Tset为母线电流建立时间；Tsam为AD采样与保持时间。

通过PWM移相的方法可以有效解决最小采样时窗的问题，但是也带来了新的问题，即当系统运行在高调制度时，PWM移相会出现饱和溢出的情况[6]，不能达到最优的移相效果，从而影响电流采样的有效性，甚至有可能出现电流重构失败。本文针对上述的问题，研究了一种改善移相饱和的PWM移相方案，对传统的PWM移相方案进行了优化，并在基于新塘公司NM1200芯片的矢量控制平台上进行实验，对算法进行了验证。

1 相电流重构的基本原理

基于单电阻采样母线电流重构出相电流的关键点在于，母线电流与相电流在不同开关状态时具有一定的对应关系。我们可以依据这种对应关系，从母线电流中分离提取出两相的相电流，再依据基尔霍夫电流定律得到三相的相电流。

为了实现单电阻电流重构方案，本文采用目前广泛运用的7段式空间矢量脉宽调制(SVPWM)作为调制策略。单电阻采样的电路结构如图1所示。图中Rshunt为母线电流采样电阻，电流流进电机的方向为三相相电流的正方向。三相逆变器上桥臂的开关状态为Sa,Sb,Sc，导通时定义为“1”，关断时定义为“0”。由此可组合形成8种空间电压矢量，如图2所示。其中6个非零基本电压矢量为U1(001)，U2(010)，U3(011)，U4(100)，U5(101)，U6(110)，2个零矢量为U0(000)，U7(111)。由此将整个空间电压矢量平面划分为6个扇区。

图1 单电阻电流重构电路结构图

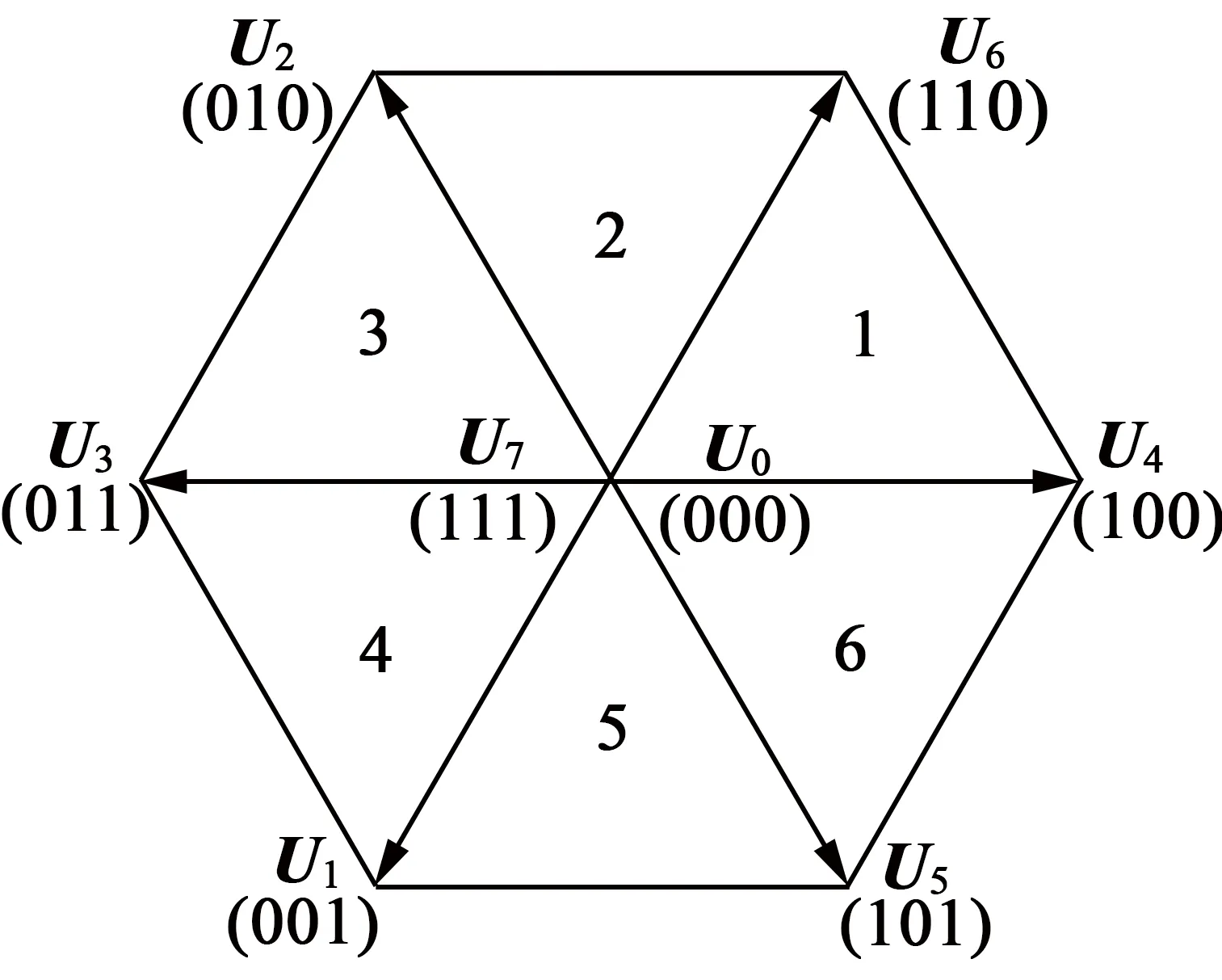
图2 SVPWM空间电压矢量图

以第一扇区为例，当给定电压矢量在第一扇区时，电压矢量由U4(100)，U6(110)组成，作用时间分别为T1,T2。在基本矢量U4(100)作用时，A相桥臂上管Q1导通，B,C相桥臂下管Q4,Q6导通，如图3所示。此时母线电流idc=ia，依次类推可以得到其他7个电压基本矢量作用时母线电流与相电流的关系,如表1所示。

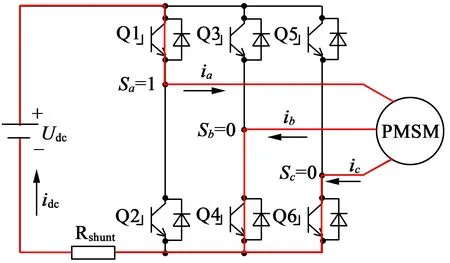
图3 基本矢量U4(110)作用时电流流向图

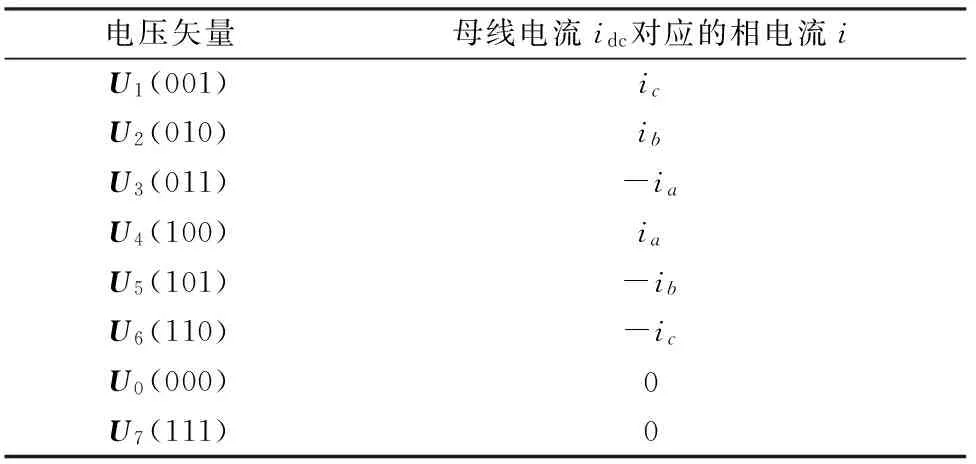
电压矢量母线电流idc对应的相电流iU1(001)icU2(010)ibU3(011)-iaU4(100)iaU5(101)-ibU6(110)-icU0(000)0U7(111)0

依据基尔霍夫电流定律有：

ia+ib+ic=0

(2)

由式(2)以及表1可得：

idc=iaSa+ibSb+icSc

(3)

依旧以第一扇区为例，分析PWM脉冲序列与直流侧idc的关系，如图4所示。

图4 第一扇区SVPWM波形示意图

在2个零矢量U0(000),U7(111)作用时，逆变器交流侧与直流侧无能量交换，此时直流侧电流idc不代表交流侧任何相电流。

2 单电阻电流重构难点分析

2.1 非观测区域

在非零的基本电压矢量作用的时候，以第一扇区为例，当U4(100)作用时，直流母线上对应的相电流为ia，U6(110)作用时，直流母线上对应的相电流为-ic，通过AD采样，我们可以得到这一时刻的相电流信息，但是为了确保采样到的电流信息是有效的，就要保证采样时间满足最小的采样时窗：

(4)

这个最小采样时窗Tmin与式(1)中的最小采样时窗保持一致。

一般来说，在空间电压矢量平面上，存在两类观测盲区。

第一类是低调制度区域，如图5中间区域所示，

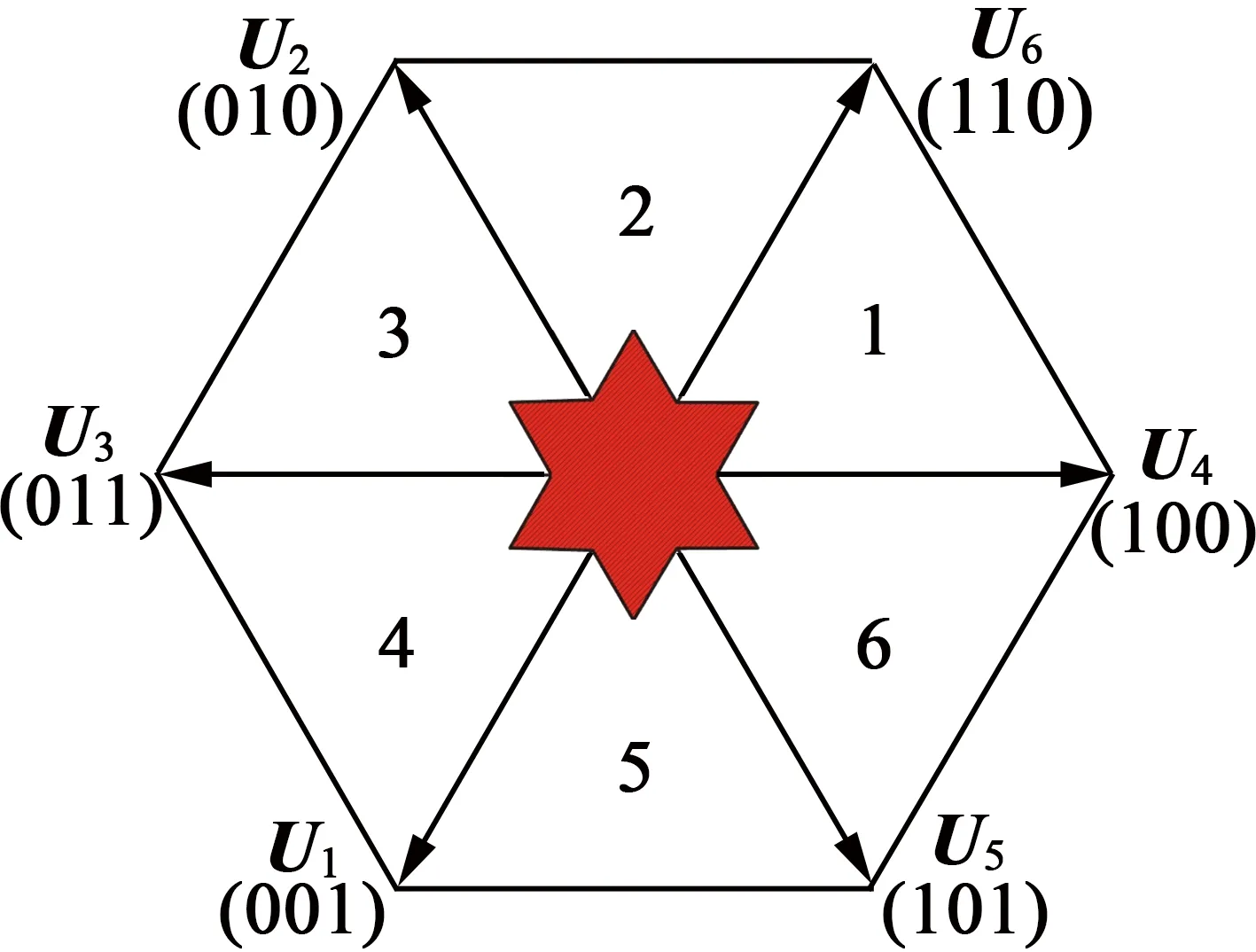
图5 低调制度非观测区

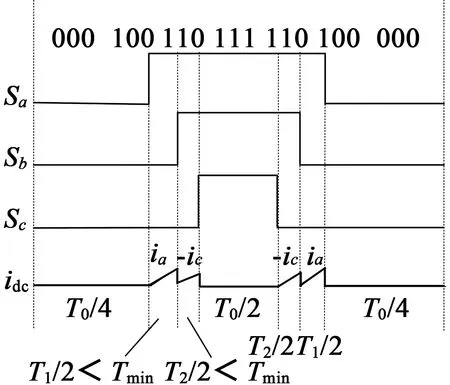
图6 第一扇区低调制度非观测区PWM脉冲信号

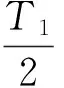
图7 扇区过渡非观测区

图8 扇区过渡非观测区PWM脉冲信号

2.2 单电阻采样相电流重构PWM移相法

本节先给出理论论证，并在此基础上利用PWM移相法来解决非观测区域的问题。

在7段式SVPWM调制方式中，给定电压矢量可以表示：

(5)

式中：Vref为给定电压矢量；Vi为某一基本电压矢量；ti为Vi的作用时间；Ts为开关周期。以第一扇区为例，结合图9进行说明。

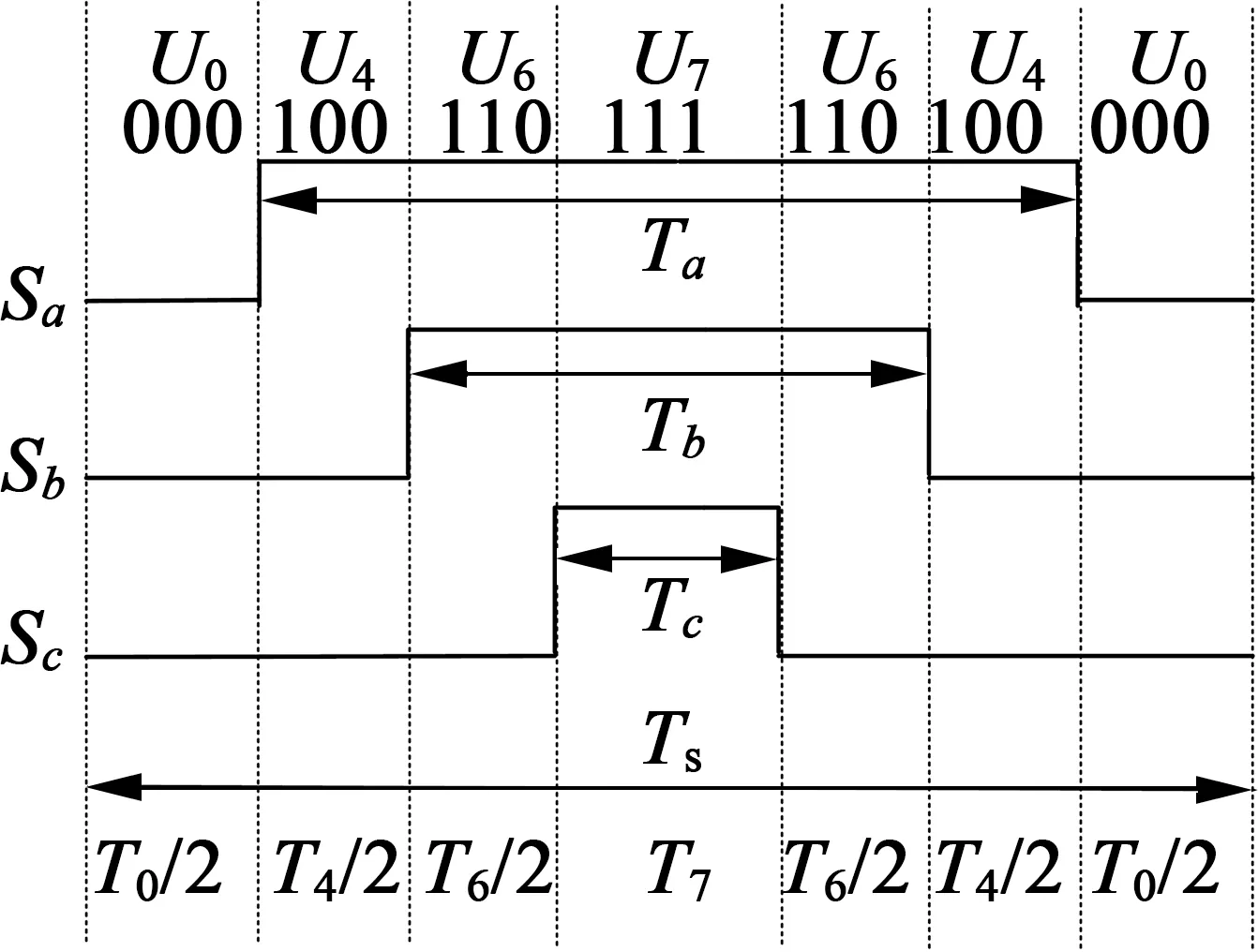
图9 第一扇区SVPWM脉冲信号

由于在第一扇区中，U1,U2,U3,U5作用时间为零，因此，式(5)可以进一步改写：

Vref=t0U0+t4U4+t6U6+t7U7

(6)

为了推导清晰，将式(6)改写：

(7)

同时，我们注意到：

(8)

(9)

式中：Ta，Tb，Tc分别表示三相桥臂上管导通时间。进而可以得到：

(10)

只要保证这3个矢量的作用时间不发生变化，那么合成电压矢量就不会发生变化。PWM移相的总体思想就是依据以上推导来进行的。

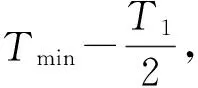
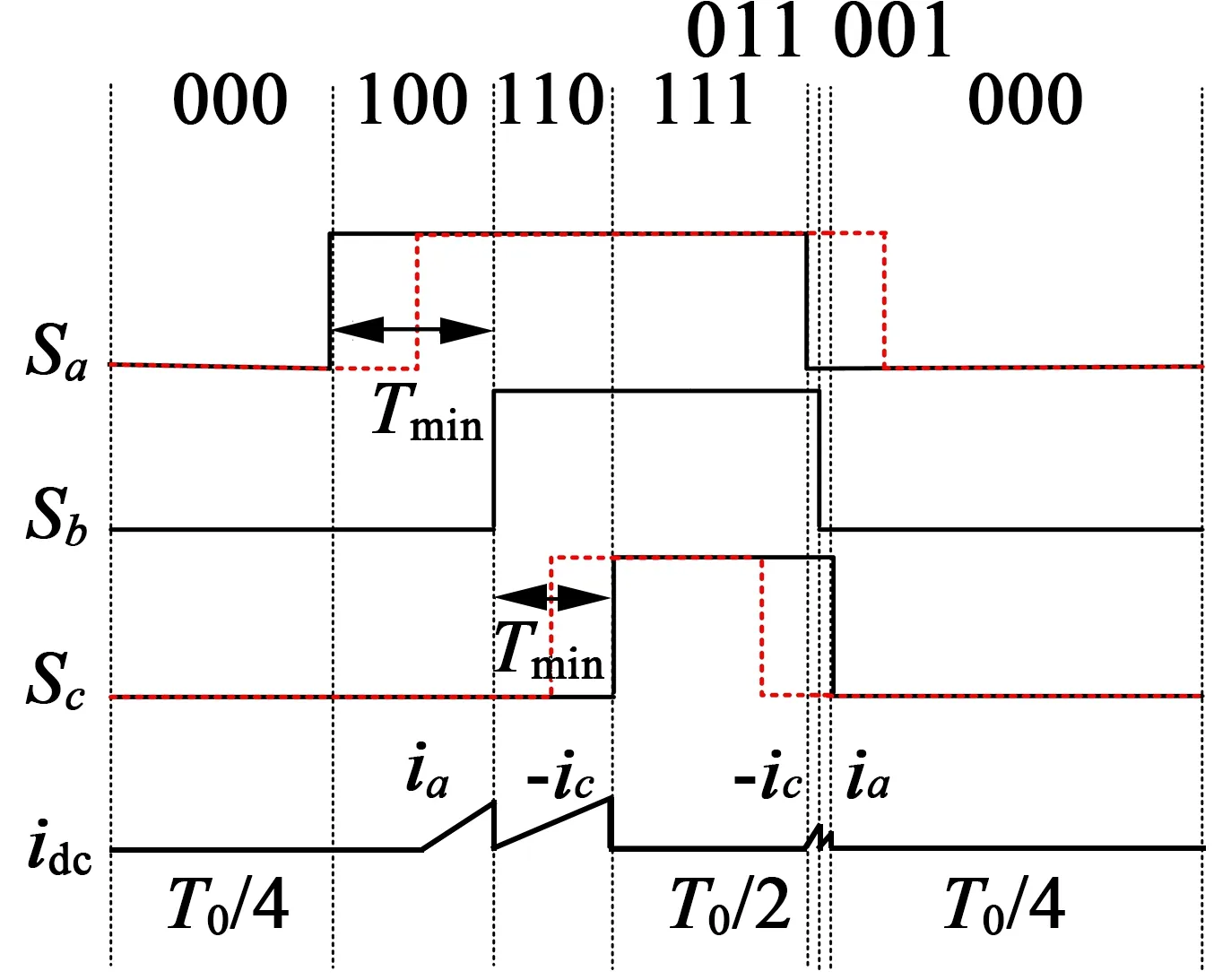
图10 第一扇区PWM移相

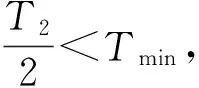
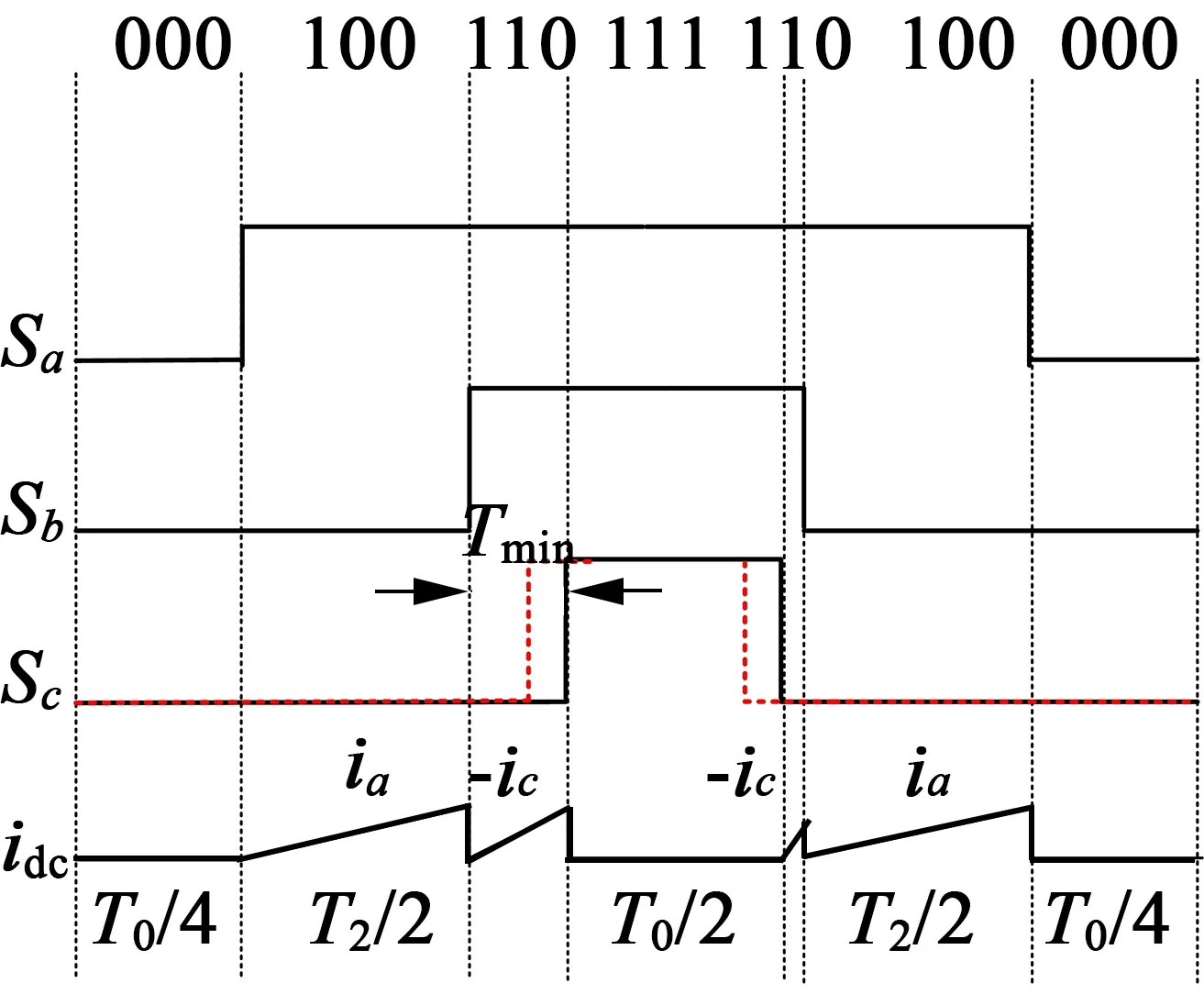
图11 扇区过渡区域PWM移相

2.3 PWM移相饱和分析及解决办法

PWM移相法虽然能解决非观测区域的问题，但同时也带来了新的问题。当在高调制度时，PWM移相会出现饱和溢出的情况[6]。以第一扇区为例，结合图12进行说明。

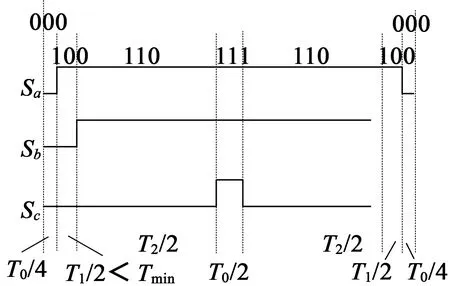
(a) 最大相左移饱和

(b) 最小相右移饱和

为了优化PWM移相算法，解决在高调制度情况下移相饱和问题，我们将PWM脉冲分成8种情况，分别进行分析说明。

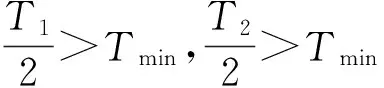
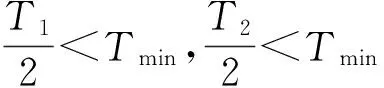
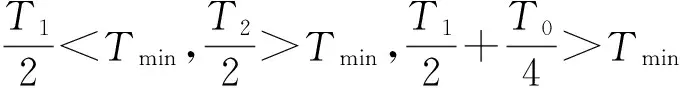
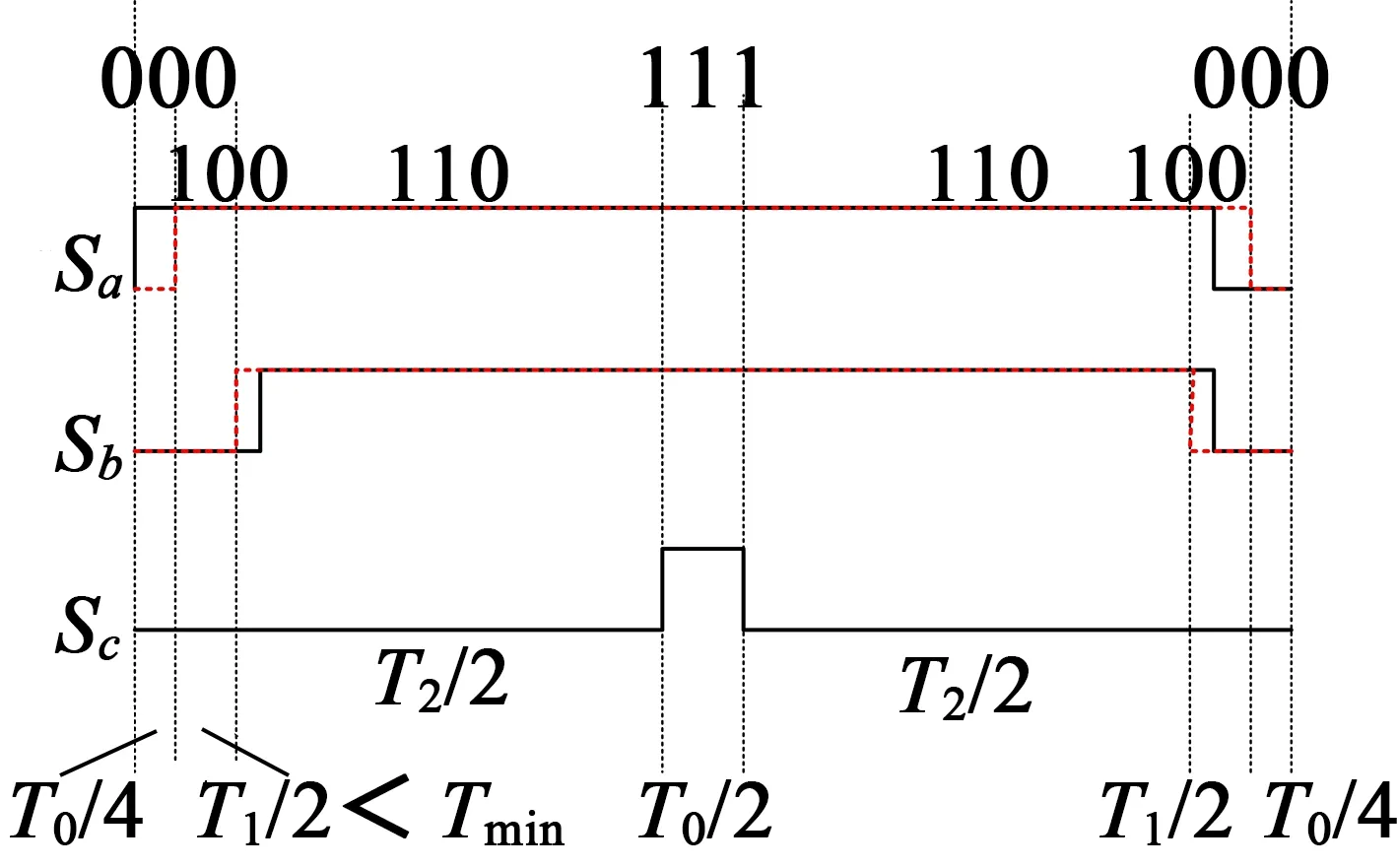
图13 最大相左移、中间相右移

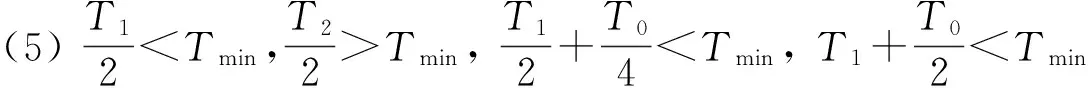
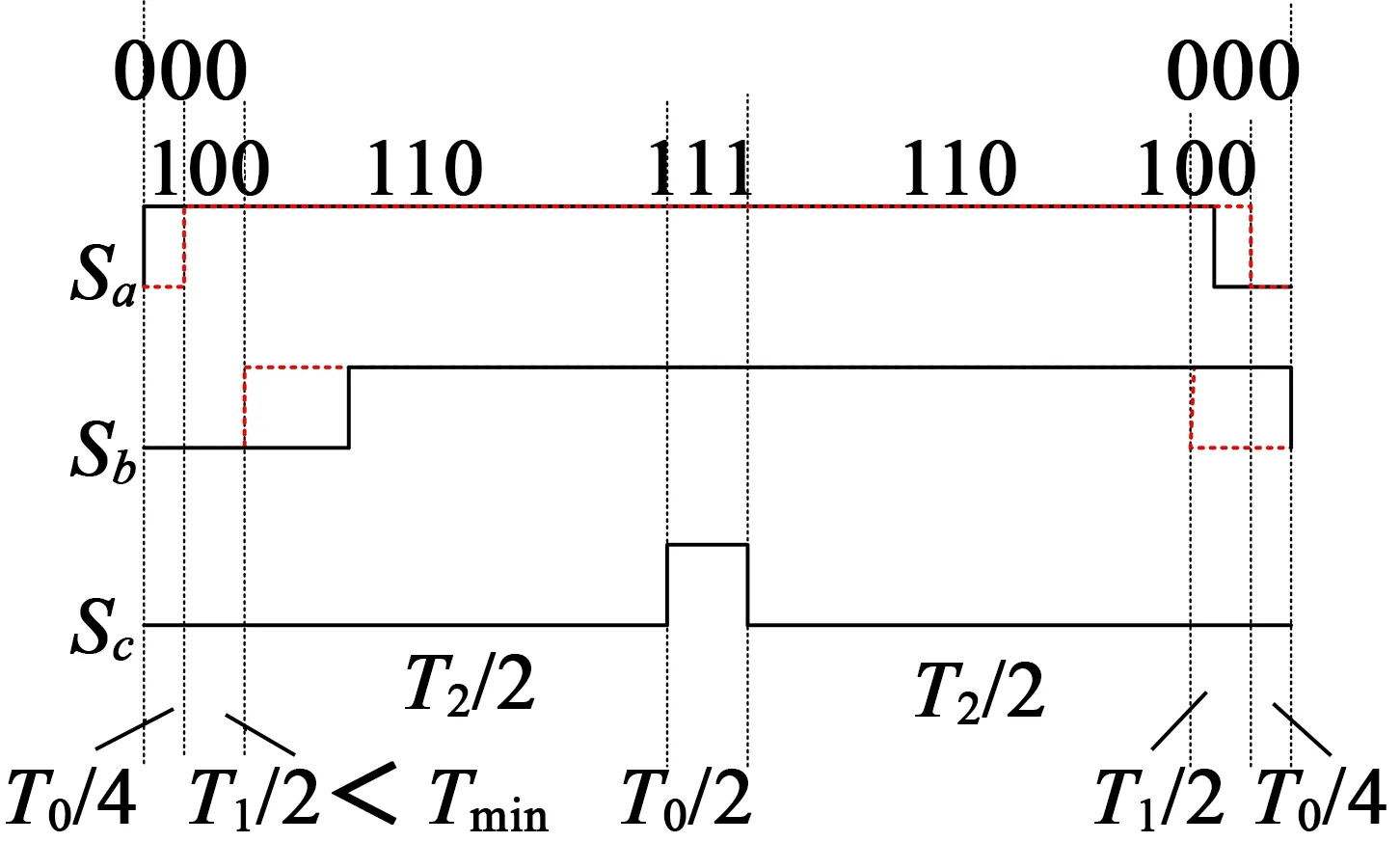
图14 中间相右移极限情况

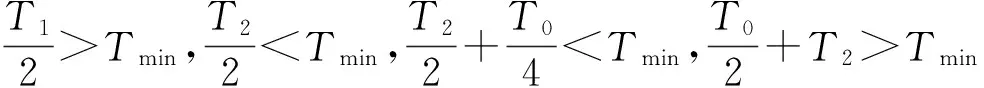
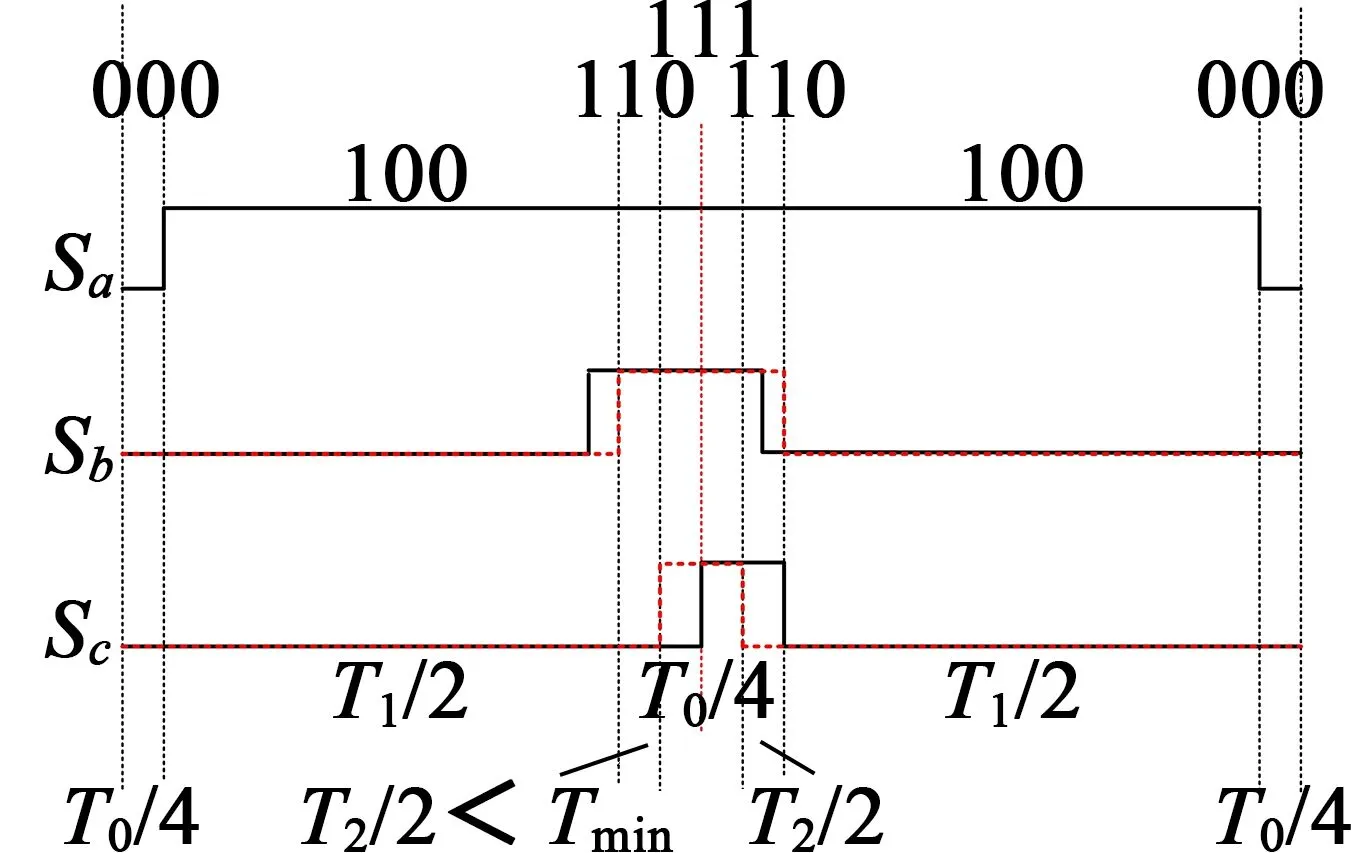
图15 最小相右移、中间相左移

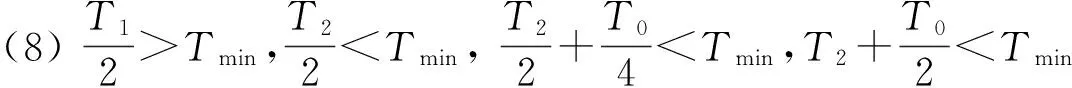
图16 中间相左移移极限情况

图13～图16中，虚线表示PWM移相前脉冲信号，实线为PWM移相后脉冲信号。通过理论分析可得出，采用移动中间占空比最小相可以扩展最大调制度限制，改善PWM移相饱和问题。虽然不能完全解决移相饱和问题，但是对移相饱和带来的问题有很大改善。

3 仿真及结果分析

为了验证PWM移相算法实现电流重构的效果，本文利用MATLAB/Simulink环境搭建了仿真模型，给出仿真条件与仿真波形，验证PWM移相法单电阻电流重构理论以及PWM移相饱和解决方案的正确性。

仿真数据如下：永磁同步电机为凸极式，定子绕组电阻为0.5 Ω，定子绕组q轴电感Lq=0.66 mH，定子绕组d轴电感Ld=0.33 mH；极对数为23；电机模型是恒转矩电流比模型，开关频率5 kHz；直流母线电压60 V；电流采样的最小采样时窗设置为8 μs。

首先，进行PWM移相法的仿真，如图17所示，转速给定为100r/min，在0.2s时，电机负载由3N·m加载到5.5 N·m。图17中，虚线为实际A相相电流，实线为重构的A相相电流。为了进一步验证效果，我们还增加了转速为50r/min和150r/min的仿真波形，如图18所示。

图17 100 r/min时实际相电流与重构相电流

(a) 50 r/min时

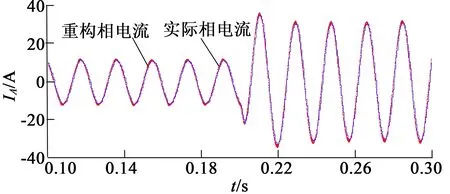
(b) 150 r/min时

在保持原有仿真条件的基础上，我们又进行了PWM移相饱和问题解决方案的仿真验证，转速给定为100 r/min，但负载由2 N·m增大到8 N·m，以保证电机运行在高调制区域。不加入移相饱和处理机制时，相电流的实际波形与重构波形如图19所示。

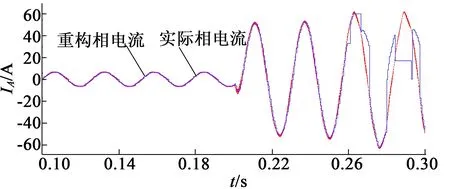
图19 未加入移相饱和处理电流

在低调制度区域，实际相电流与重构的相电流均正常，但是到了高调制区域，可以很明显地发现重构的相电流发生了严重的畸变，这是由于进行PWM移相出现了饱和溢出，所重构出的相电流已经无法复现实际相电流。

加入PWM移相饱和处理机制之后，如图20所示。可以发现，相对于未加入饱和处理的波形，在高调制度区域重构相电流畸变减小，重构失败的几率大大减小，且所重构出的相电流基本能复现实际相电流，效果可观。

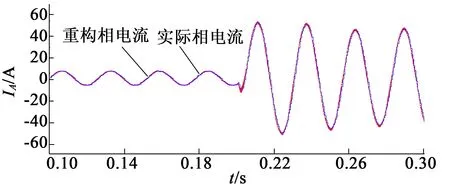
图20 加入移相饱和处理相电流

综上，利用PWM移相法可以有效地重构出电机的相电流，但是在高调制度会出现移相的饱和溢出现象，从而导致重构的效果变差；PWM移相饱和处理方法能够有效地扩宽最大调制度的限制，有效地改善了高调制区域电流重构失败的问题。

4 实验验证

为验证本文研究算法的有效性， 在基于新塘公司NM1200芯片的矢量控制平台上进行实验验证。实验用电机为永磁同步电机，额定电压为24 V，极对数为2，额定功率为92W，额定转速为3500 r/min。

首先我们进行电机的开环运行实验，并在磁粉测功机上对电机进行测试。设定电机开环转速给定为3 200 r/min，观察相电流的重构效果，如图21所示可以看出，重构的相电流与实际的相电流吻合度较高，达到了预期的效果，同时也说明电流重构算法是有效的。

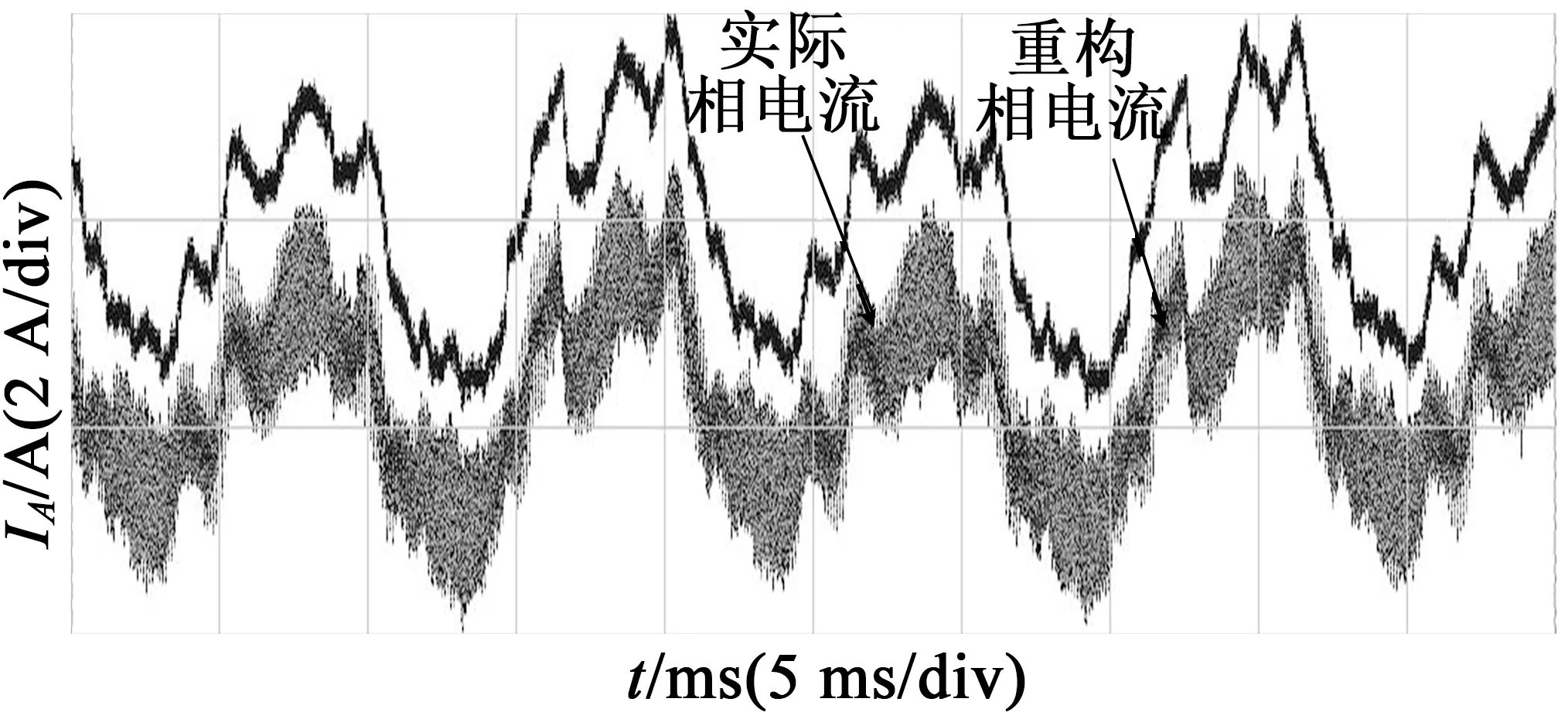
(a) 空载运行

(b) 带载运行

为了进一步验证算法，进行闭环实验，转速给定设置为3 200 r/min。

闭环实验效果如图22所示。通过观察，我们可以清楚地发现实际相电流与通过DA打出来的重构相电流波形二者基本一致，不存在相位偏差，重构效果完好。

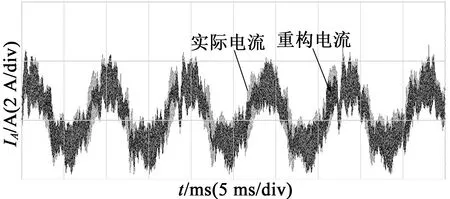
(a) 空载运行

(b) 带载运行

5 结 语

本文详细分析了PWM移相单电阻电流重构算法的基本原理，并在分析原有算法缺点的基础上，介绍了一种改善PWM移相饱和的单电阻电流重构优化算法。此后，在MATLAB/Simulink仿真环境中，对基本的单电阻电流采样电流重构的矢量控制算法以及加入防止移相饱和机制的PWM移相优化算法进行仿真验证，优化算法的引入提升了相电流重构的可靠性。最后，在矢量控制平台上进行了实验验证，在开环以及闭环的条件下重构效果均十分理想。综上，本文的优化算法是正确、可行的。

[1] 储剑波,胡育文,黄文新,等.一种变频器相电流采样重构技术[J].电工技术学报,2010,25(1):111-117.

[2] 陈小波,黄文新,胡育文,等.变频器单电阻电流采样及相电流重构方法[J].电气传动,2010,40(8):3-6.

[3] 杜凡,李云辉,魏延羽,等.两种基于母线电流传感器的相电流重构方法[J].微电机,2013,46(12):55-59.

[4] 李云辉.永磁同步电机相电流重构技术研究[D].哈尔滨：哈尔滨工业大学,2014.

[5] 储剑波.驱动空调压缩机的永磁同步电动机的控制技术研究[D].南京：南京航空航天大学,2010.

[6] KIM H,JAHNS T M.Current control for AC motor drives using a single DC-Link current sensor and measurement voltage vectors[J].IEEE Transactions on Industry Applications,2006,42(6):1539-1547.

[7] AOYAGI S,IWAJI Y,TOBARI K,et al.A novel PWM pulse modifying method for reconstructing three-phase AC currents from DC bus currents of inverter[C]//International Conference on Electrical Machines and Systems.IEEE,2009:1-6.

[8] KIM H,JAHNS T M.Phase current reconstruction for AC motor drives using a DC link single current sensor and measurement voltage vectors[J].IEEE Transactions on Power Electronics,2006,21(5):1413-1419.

[9] GU Y,NI F,YANG D,et al.Switching-state phase shift method for three-phase-current reconstruction with a single DC-link current sensor[J].IEEE Transactions on Industrial Electronics,2011,58(11):5186-5194.