基于格林函数的永磁同步电机瞬态温度计算方法

彭润泽，张 琪，黄苏融，刘朋鹏，郭建文

(1.上海大学，上海 200072;2．上海大郡动力控制技术有限公司，上海 201114)

0 引 言

伴随着效率、成本以及材料利用率要求的不断提高，高密度永磁同步电机的电磁负荷和热负荷选取趋于极限，导致单位体积发热量明显增大，带来了严重的发热问题。过大的发热量导致温升超过材料允许的承受范围，进而破坏其物理属性，甚至导致永磁体的不可逆退磁以及绕组绝缘材料被击穿[1-2]。因此，准确计算永磁同步电机内部温度，特别是一些局部过热点温度，具有十分重要的意义。

常用的永磁同步电机温度计算方法主要有简化公式法、等效热网络法和基于计算机商用软件的仿真方法等。简化公式法算法相对简单，但误差较大。等效热网络法只能得到电机各部件的平均温升，其优点是计算快速、传热路径清晰，便于方案评估,但是，目前的热网络模型计算精度难以保证。基于计算机商用软件的仿真方法可以分为有限元分析和计算流体力学，这2种分析方法都能准确计算电机的瞬态温升与温度分布，但都极其依赖于几何模型以及计算机运算能力，且耗时较多[3-5]。

电机中各部件的温度值是边界条件、各发热源以及前一状态温度值构成的复杂函数。在实际应用中，电机经常工作在额定运行、峰值运行和停止等多种不同工况，难以精确计算电机温升。文献[6]提出了一种计算全封闭式风冷异步电机瞬态温升的响应函数法。这种方法引入格林方程,并将其视为一种可以用有限元法得到的函数。本文将在此基础上进一步展开研究，提出了一种基于格林函数的水冷式永磁同步电机温升计算方法，并考虑了不同工况对响应函数的影响。该方法通过求解电机内的导热方程，可以计算任意工况下永磁同步电机中任意点的瞬态温度和任意部件的平均瞬态温度。本文还以一台48槽8极水冷式永磁同步电机为例，将该计算方法结果与有限元仿真、实验数据进行比较，吻合度较好，验证了其有效性。

1 电机内导热方程的求解

1.1 格林函数法求解单一物体的导热方程

假设热传导系数、密度、比热容和散热系数不随温度的变化而变化，则可以认为各发热体构成的系统是一个线性系统，满足叠加定理。

针对单一热源的热传导方程在直角坐标系下可表示：

(1)

三类边界条件可统一表示：

(2)

式中：n表示边界S面上沿界面外法线方向的导数；h表示边界S上的散热系数；f表示边界函数。

假设式(1)的初始条件：

T(p,t)t=0=0

(3)

应用格林函数法求解瞬态导热方程式(1)，得到解：

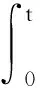
(4)

式中：G11为在边界条件脉冲函数下的温度响应格林函数；G12为在热源脉冲函数下的温度响应格林函数。对于几何形状复杂的物体，G11和G12通常是不具有解析解的[7]，因此需要借助有限元法辅助得到G11和G12。式(4)的离散化形式可表述：

(5)

也可以表达为卷积运算形式：

T(p,t)=G11(p,t)*f(t)+G12(p,t)*qv(t)

(6)

式中：*表示卷积运算。

1.2 格林函数法求解多物体的导热方程

多个物体的传导方程中的各个系数将会因为物体物理性质而不同。以2个物体组成的系统为例。假设2个物体接触面之间的热流不会损失，如图1所示。

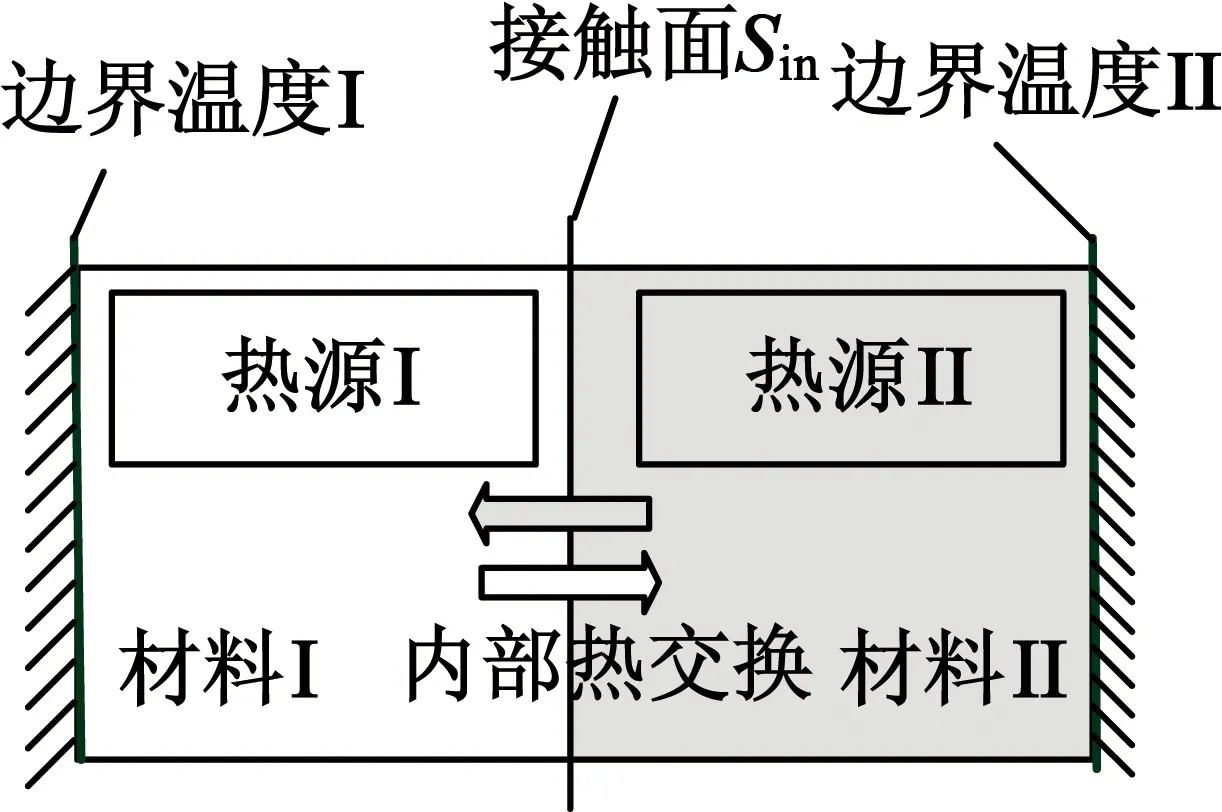
图1 2个接触物体的热传导情况

因此，接触面边界方程：

(7)

式中：qin是2个物体之间交换的热量；k1和k2分别表示材料I和材料II的热传导系数；Sin表示接触面。

同样假设初始条件均为0，同理可以得到2个物体构成的系统的瞬态温度解：

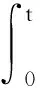
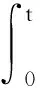
(8)

式中：G21为物体二的边界条件脉冲函数下的温度响应格林函数;G22为物体二的热源脉冲函数下的温度响应格林函数。

同理，多个物体的离散化求解表达式可以由2个物体的情况推广而得，可表示：

(9)

式中：m取决于边界数；n取决于热源数量。

1.3 格林函数法的等效变换

式(9)提供了求解电机内任意点瞬态温升的离散解析表达式。但是，脉冲函数在t=0时刻存在奇异性，不易在仿真软件中实现，因此还需要利用卷积的杜哈美尔积分性质对其进行等效变换，如图2所示。

图2 格林函数等效变换示意图

若设F为单位阶跃响应函数，则有：

(10)

对于同一线性系统，根据图2的等效原理，对式(9)进行变换，可得：

(11)

式中：Δfi和Δqvj分别为物体i的边界条件对离散时间的增量和物体j的单位热源对离散时间的增量。

同样地，物体的平均温升可表示：

(12)

式中：Fi1-av为物体i的边界条件单位阶跃函数下的平均温度响应格林函数；Fj1-av为物体j的单位热源阶跃函数下的平均温度响应格林函数。式(11)和式(12)分别是计算某一点和部件平均温升的格林函数法离散解析表达式。

2 水冷式永磁电机仿真计算实例

2.1 求解模型的建立和热参数的等效

本文以一台48槽8极电机为例，其基本参数如表1所示。

表1 水冷式永磁同步电机参数

为缩短仿真时间，根据对称性原理，取单元电机为计算域，其三维温度场仿真模型如图3所示。

图3 电机仿真计算模型

图3中，点A位于定子齿顶处；点B位于绕组端部；点C位于永磁体内部。电机在仿真模型中的散热面包括定、转子端面，绕组端部，机壳外表面。其中，转子端面散热系数受转速影响较大，两者关系可表示：

(13)

式中:v为转子线速度。

由式(13)可以看出，不同工况下的转子端面散热系数是不同的，因此在计算时需要进行修正。定子端面和绕组端部的散热系数可参考文献[11]。

本文研究的永磁同步电机是通过定子外部机壳的水道冷却，由于冷却水道出水口和入水口的温度差很小[2]，因此可以认为冷却介质的温度为常值，即将机壳外冷却水道看作第三类边界条件进行等效。

气隙也是电机内部互相传递热量的一条路径，其热传导系数与多种因素有关。本文采用文献[8]提出的一种气隙热传导等效方法，其等效热传导系数λδ：

(14)

式中:Reδ为等效雷诺数;Dsi,Dro和δ分别表示定子内径、转子外径和气隙长度；n表示转速；γ表示空气的运动粘度。

2.2 基于格林函数法的水冷式永磁同步电机温度计算

水冷式永磁同步电机的瞬态温升可以通过式(10)计算，图4展示了具体流程。

图4 格林函数法计算流程图

其步骤如下：1) 使用有限元软件求取不同工况下的响应函数F；2) 确定电机运行工况，假定各部件工作温度，并判断所求工况下的响应函数F是否在步骤1中得到。若有，则进一步计算电磁性能，得到各损耗值；若无,则对其进行修正后进行下一步；3) 利用格林公式计算温升，并判断各部件的假定工作温度与计算结果之差是否满足精度要求。若满足，则得出结果；不满足,则重新修正各部件工作点温度，重新进行循环计算，直至满足要求。

2.2.1 各个热源下响应函数的求取

将样机中损耗分为绕组铜耗、定子铁耗、永磁体涡流损耗和转子铁耗4部分，并利用Fluent仿真，以转子端面散热系数h=50为例，分别在4部分中添加单位热源，得到了A,B和C三点的单位阶跃响应函数，其结果如图5所示。

从图5可以看到,各个热源对A,B和C三点的影响。A点和B点分别位于定子齿部和绕组端部，相对于永磁体内部的C点散热条件更好，所以达到稳定的时间更短。

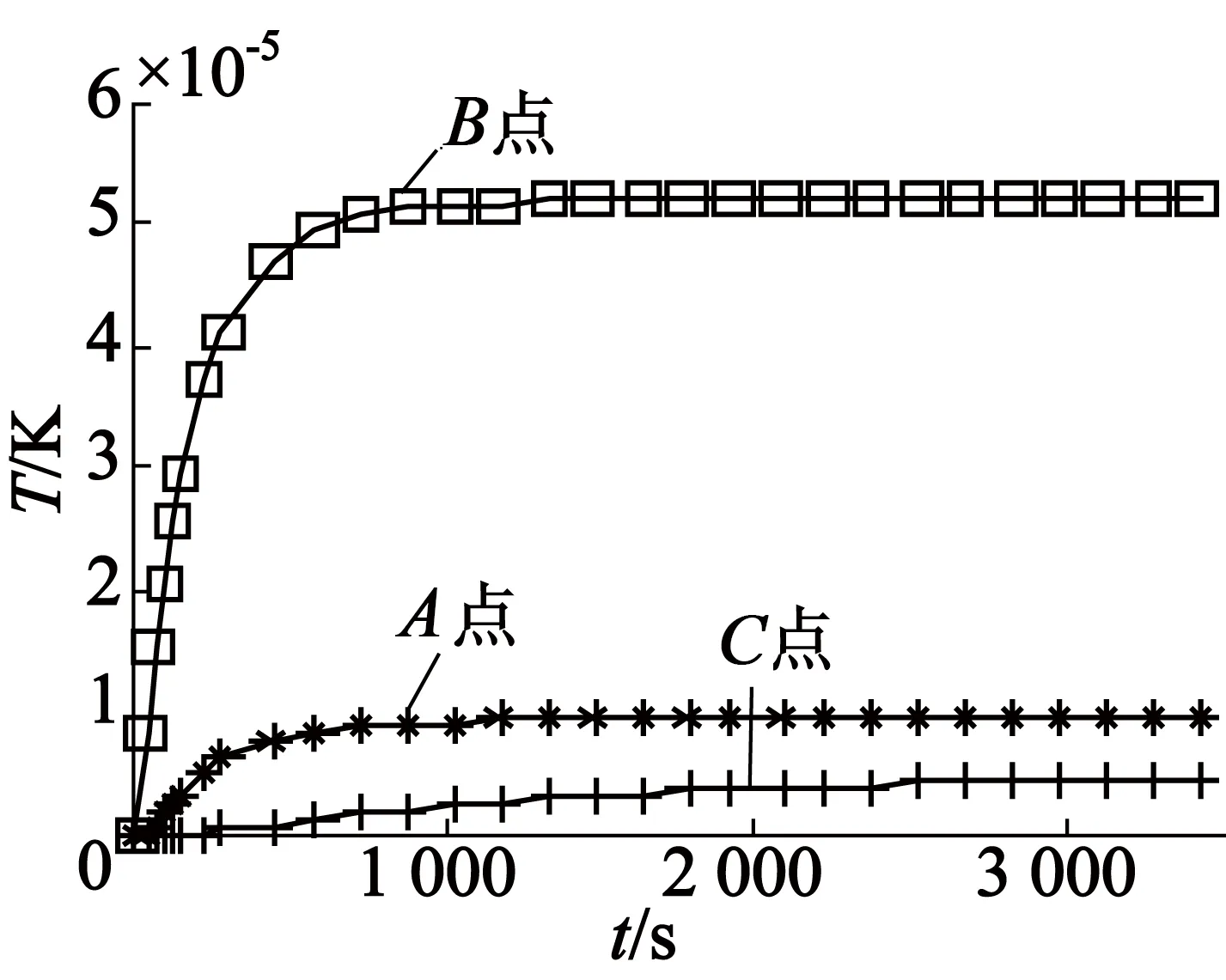
(a) 绕组单位热源下

(b) 定子单位热源下

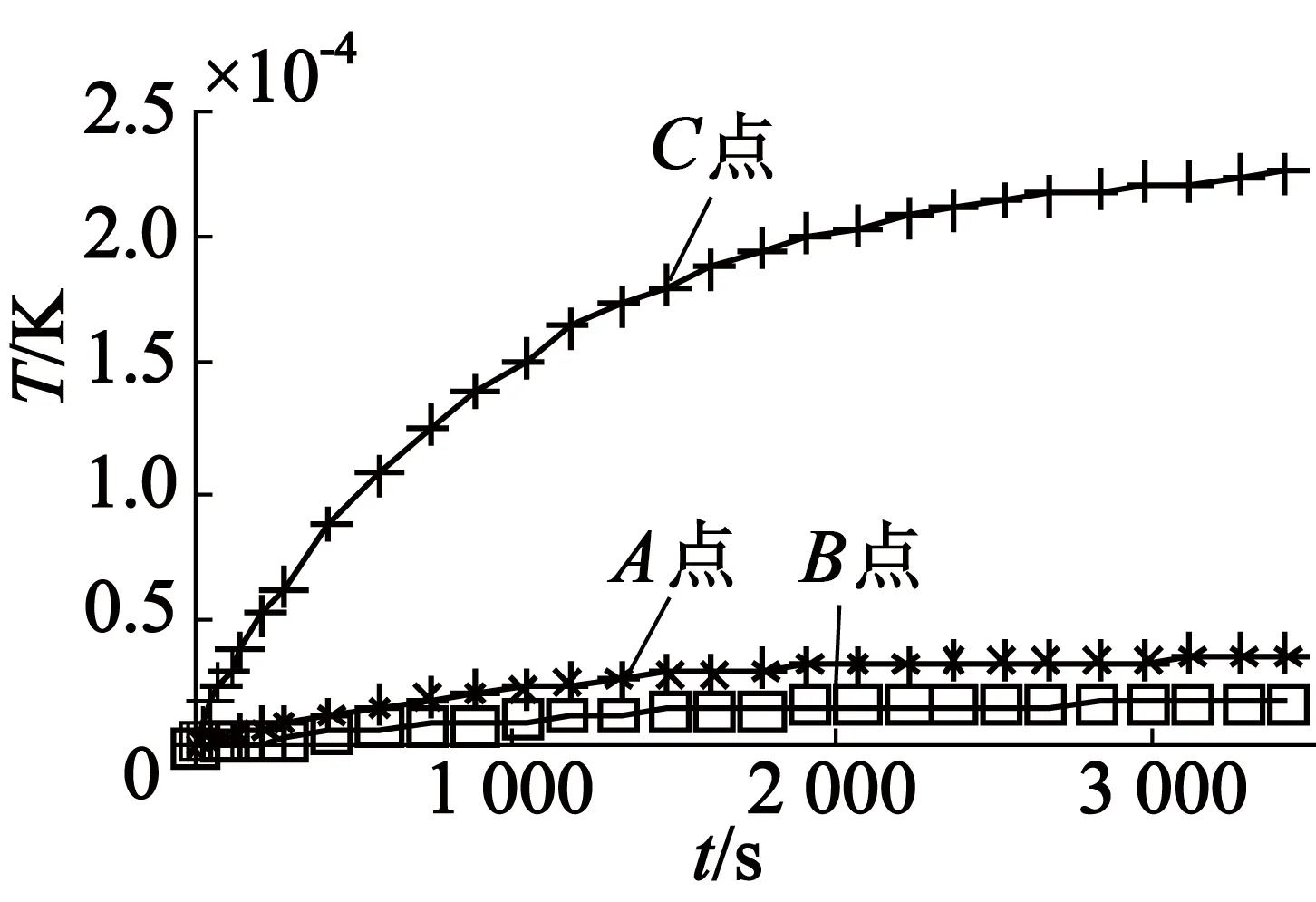
(c) 永磁体单位热源下

(d) 转子单位热源下

图54个部件添加热源时的响应函数

同理可以得到边界条件的单位阶跃函数响应。

2.2.2 不同工况下F函数的修正

由于转速直接影响转子铁心端面的散热系数，其对转子和永磁体的单位热源阶跃响应函数的影响较为明显。本文以C点为例，利用Fluent仿真得到不同散热系数下其单位热源响应函数的曲线，如图6所示。

图6 不同转子端面散热系数下的C点响应函数曲线

从图6可以看出，不同转子铁心端面散热系数会对C点温升计算造成误差，所以必须加以修正。

本文提出了一种拉格朗日插值的修正方法。采用h=50，180和380的单位热源阶跃响应函数的数据，插值计算h=280的结果，并与h=280时的Fluent仿真结果作对比，如图7所示。

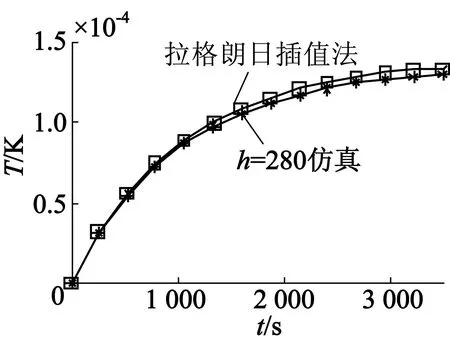
图7 h=280时C点温升拉格朗日插值与仿真对比

仿真结果表明，利用拉格朗日插值法修正不同工况下的散热系数是有效的。

2.2.3 基于格林函数法的瞬态温升计算

本文以变转速变负载情况为例，计算样机的A,B和C三点瞬态温升，其运行工况如图8所示。

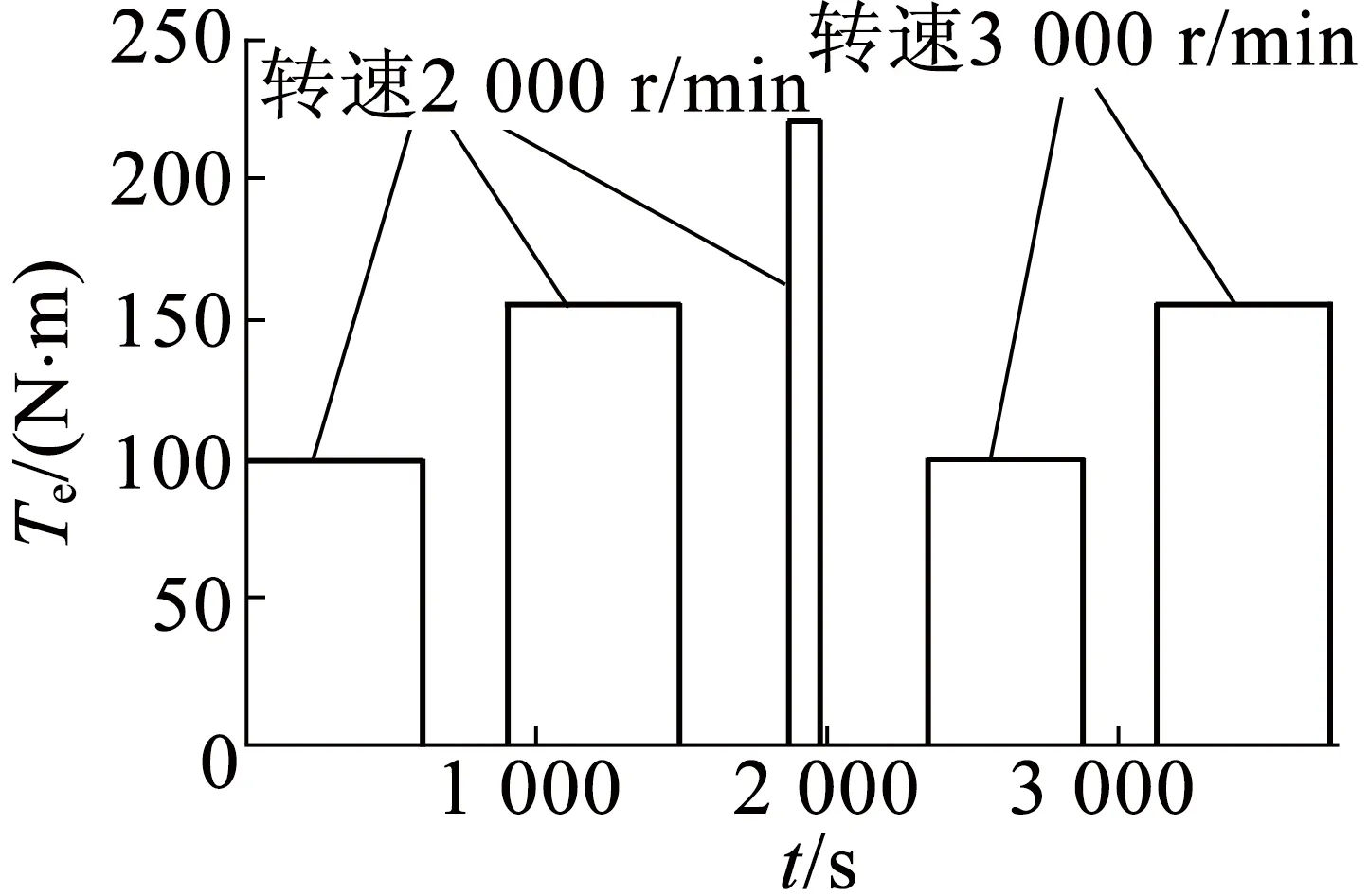
图8 电机运行状态

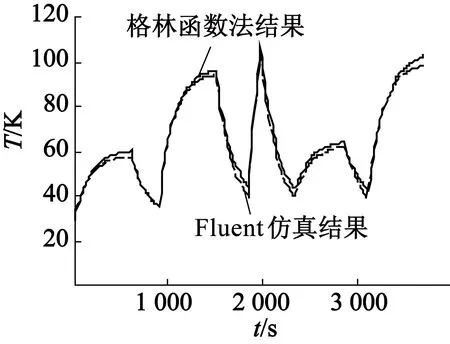
为了验证该方法的准确性，将A,B和C三点的格林函数法计算结果和Fluent仿真结果进行对比，如图9所示。

(a) A点(定子齿处)

(b) B点(绕组端部)

(c) C点(永磁体内部)

从图9可以看出，电机在变工况运行条件下，格林函数法计算结果与Fluent仿真结果吻合度较高。A点位于定子齿部，主要受定子铁耗影响；B点位于绕组端部，其温升主要是由于绕组电流产生的铜耗导致的，所以带载时温度上升较快，停转无负载时温度降低也较快；C点位于永磁体内，主要受转子铁耗与永磁体涡流损耗影响，其散热条件较差，所以受电流变化影响较小。

3 实验验证

本文以绕组端部B点为例，将格林函数计算结果与实验数据进行比较，如表3所示。

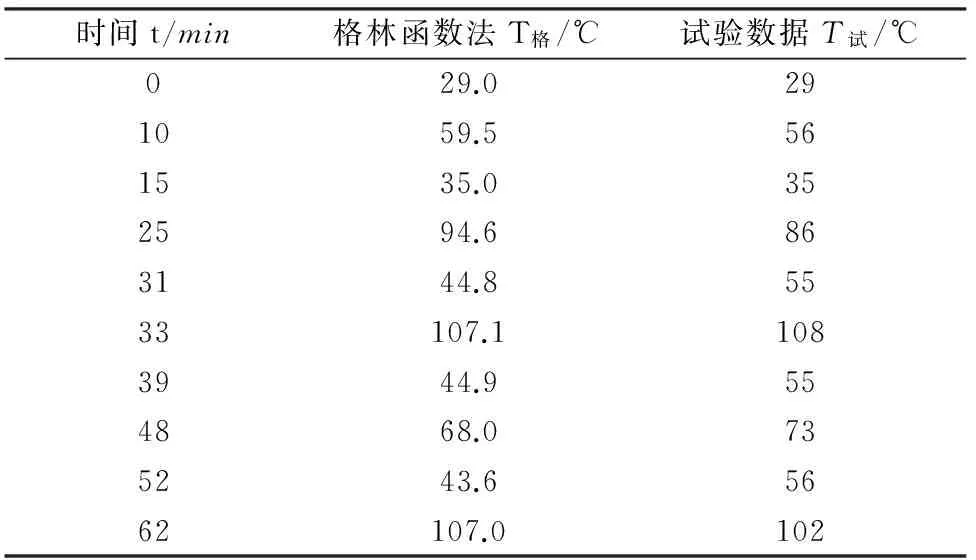
表3 实验对比

表3结果显示，格林函数法计算结果与实际测得结果基本吻合，进一步验证了该方法的正确性。

4 结 语

本文提出了一种基于格林函数的水冷式永磁同步电机瞬态温度计算的方法，该方法兼备了有限元法的准确性和解析法的快速性。为快速评估电机瞬态温升提供了一种新的方法，也为电机温度的在线监视提供了一种新的思路。

本文利用杜哈美尔积分性质，对格林函数进行等效变换，解决了有限元仿真中脉冲函数的奇异性问题，为利用格林函数法计算电机温升提供了途径。在此基础上，还考虑了电机运行时不同工况对响应函数的影响，并利用拉格朗日插值法进行修正，提高了计算精度。

文末详细讨论了基于格林函数的永磁同步电机瞬态温升计算步骤，并以一台48槽8极样机为例，将该方法计算结果分别与Fluent仿真结果、试验测试数据进行对比，吻合程度较好，验证了该方法的有效性。

[1] BOGLIETTI A,CAVAGNINO D,STATON M,et al.Evolution and modern approaches for thermal analysis of electrical machines[J].IEEE Transactions on Industrial Electronics,2009,56(3):871-882.

[2] 张琪,鲁茜睿,黄苏融,等.多领域协同仿真的高密度永磁电机温升计算[J].中国电机工程学报，2014,34(12):1874-1881.

[3] 程树康,李翠萍,柴凤. 不同冷却结构的微型电动车用感应电机三维稳态温度场分析[J].中国电机工程学报,2012,32(30):82-90.

[4] 李立毅,张江鹏,闫海媛,等.高功率密度电机三维温度场计算及导热优化研究[J].中国电机工程学报,2016,36(13):1-9.

[5] ZHANG Hengliang.Online thermal monitoring models for induction machines[J].IEEE Transactions on Energy Conversion,2015,30(4):1279-1287.

[6] Kazuo Ohtaka.Mathematical Tools for Physicists[M].New York:WILEY-VCH,2005:159-172.

[7] XYPTRAS J,HATZIATHANASSIOU V.Thermal analysis of an electrical machine taking into account the iron losses and the deep-bar effect[J].IEEE Transactions on Energy Conversion,1999,14(4):996-1003.

[8] Филиппо И Ф.电机中的热交换[M].杨斌译.北京:原子能出版社,1989:14-33.