无刷直流电动机测试平台系统的实时优化控制

杨 洁，卫 宏

(1.正德职业技术学院，南京 211106；2. 南京林业大学，南京 210037)

0 引 言

近年来，工业生产制造过程中的生产质量、安全和经济性要求越来越高，学术界和工业界都对其较为关注，从而最优控制、鲁棒控制、故障检测和隔离FDI(fault detection and isolation)和容错控制技术已成功应用于大量的工业过程控制中[1-5],包括电机测试等。特别将FDI融入反馈闭环控制是一种流行趋势[6-7]。然而，离线优化设计难以保证工业自动控制系统的全寿命周期最优运行，具体原因：系统的未知或意外干扰不可避免；控制对象模型和实际设备存在一定程度的不匹配；运行条件或参数较易发生变化；组件的更换或维修也带来了不确定性。针对这些原因，许多先进的控制技术得到了研究和发展，以期达到更好的控制性能。然而真正能付诸实践的方案较为鲜见，因为大多数情况下，预先设计的复杂工业流程的控制系统不允许中途修改参数，故难以实现真正的匹配。

在工程实践中，PI或PID控制器应用广泛，设计技术也很成熟；同时存在许多在线PI或改进型PID技术以解决上述问题[8-9]，但普遍存在调节性能和稳定性的折衷。此外，对于采用PI或PID控制的实际装置，确定其在线稳定域非常困难，从而控制性能受限。基于此，本文提出了一种集成过程监控和控制的新型结构，解决已存在闭环控制器的稳定性问题，即通过在线迭代优化实现参数化矩阵，以保证稳定性。虽然有很多参数化矩阵设计方法已被提出[10-11]，但主要的关注点在于基于状态观测器的闭环状态反馈控制问题，而工业应用中，这些方法需要用基于状态观测器的闭环状态反馈控制器替换现有的PI或PID控制器。故本文所设计的方案加强了控制系统的鲁棒性，同时不影响原有预设跟踪性能，且较其他方法更为简单和易于实现。最后，以无刷直流电动机测试平台为对象，进行了新型方法的应用和试验验证。

1 工控系统优化问题建模

1.1 Youla参数化矩阵描述

考虑可镇定和可观测的标称系统G(z)具有状态空间形式：

(1)

(2)

(3)

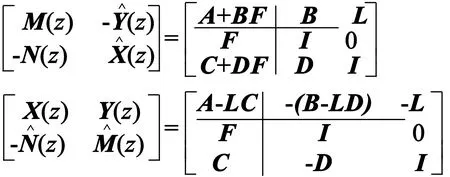
选择合适的F和L将使得A+BF和A-LC都稳定。

1.2 优化问题模型

为了处理模型不确定性和内部受控对象故障，我们考虑一个一般受控对象Gg(z)：

(5)

图1 标准的闭环反馈控制系统

下面将引入引理1[14]进行标准闭环反馈控制系统的稳定性分析。

引理1：设K(z)是一个具有传递函数形式为式(2)的控制器，则下面两个判据是等效的。

为了简化工程实现难度，下一节将研究基于现有标称反馈控制器K(z)的Youla参数化替代实现方案。这个方案将实现整个控制系统的性能改进，而不修改或替换预先设计的控制系统，方案的实施过程则是一种实时迭代鲁棒优化过程。

2 自动控制系统在线优化策略

2.1 Youla参数化替代实现方案

基于Youla参数化，引入引理2，并作为后续研究基础。

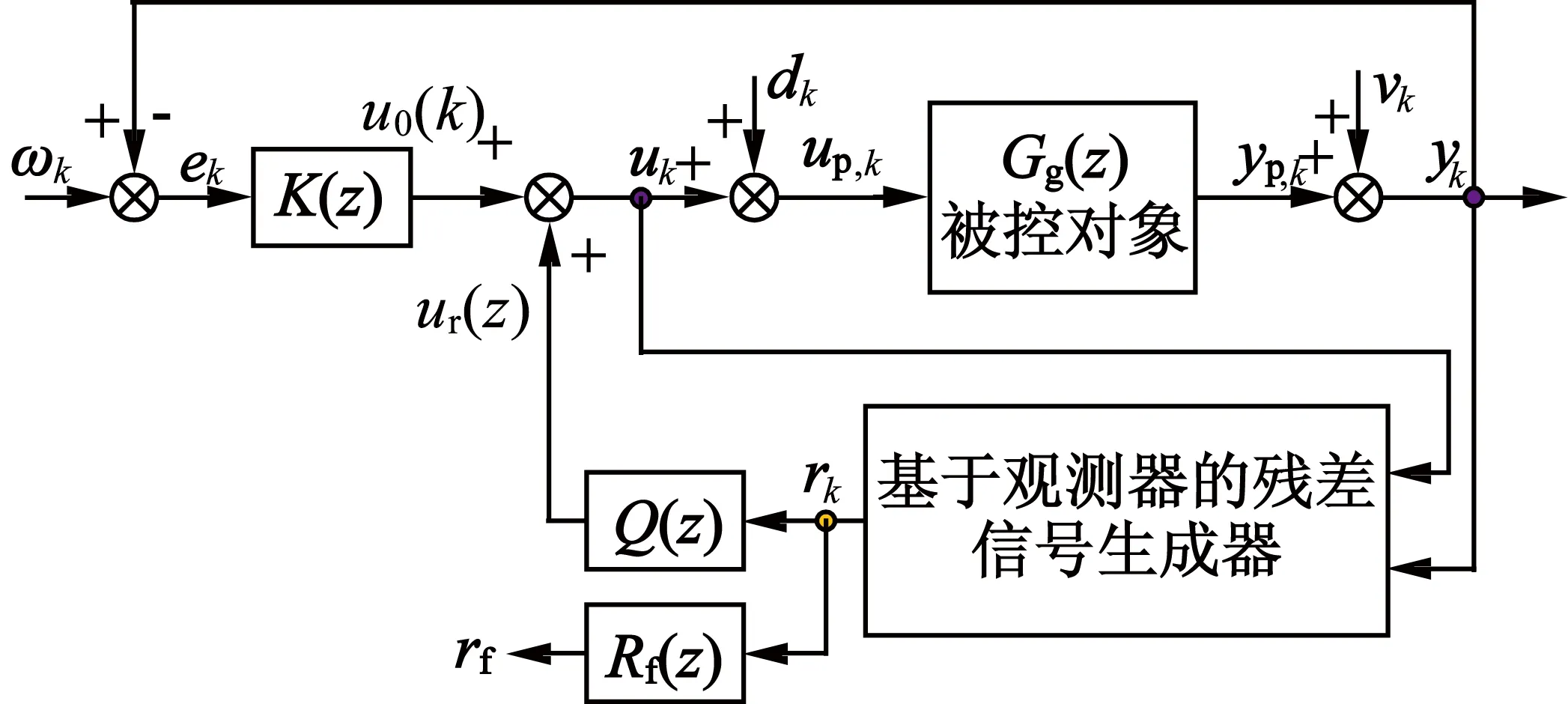
图2 现有闭环系统Youla参数化实现

(6)

系统参数化替代实现方案提供了一个过程控制的集成设计和监控解决方案：一方面，监控残差矢量可以用于FDI；另一方面，控制器设计也变得更容易，设计时考虑Q(z)∈RH∞，即可保证系统稳定性。也就是说，给定一个现有的、具备较好的跟踪控制性能，稳定控制器K(z),则可以通过设计满足式(6)的参数化矩阵Q(z)，使得原有控制器鲁棒性更好，从而较好地应对模型不确定性、故障和干扰。

近年来，文献[15]提出了基于数据驱动技术的核和图像表示实现方法。基于此，本文设计了利用控制过程中输入和输出数据的基于观测器的故障检测与控制系统。

2.2 Youla参数化矩阵在线优化

在图2中可以看出，标称控制器K(z)可以确保稳定性和跟踪性能，但不一定能达到令人满意的鲁棒性。通过引入参数化矩阵Q(z)∈RH∞，则可以容易地增强原系统的鲁棒性而不影响闭环稳定性和跟踪控制性能。如果残差信号r(k)=0，则图2中的系统结构还原为原始控制系统结构，但如果r(k)≠0，一般是由未知扰动、模型不确定性或故障导致的，这时设计参数化矩阵Q(z)可以提高系统的鲁棒性。为了实施图2的控制系统结构，并在线配置Q(z)，首先应用数据驱动技术构建了基于观测器的残差发生器，其通常具有如下的状态空间表述：

zk+1=Azzk+Bzuk+Lzrk

(7)

(8)

(9)

Az=TAT-1,Bz=TB,Cz=CT-1,Dz=D

(10)

xr,k+1=Arxr,k+Brrk

(11)

ur,k=Crxr,k+Drrk

(12)

式中：矩阵Ar中的“*”代表可能的非零元素，xr,k∈Rq为状态矢量，Ar∈Rq×q为所设计的稳定矩阵。通常选择矩阵Ar的特征值与观测器动态矩阵Az-LzCz的特征值在幅值上具有可比性。Cr∈Rl×q和Dr∈Rl×m为Q(z)的设计参数，因此可注意到：

θc=col(Cr)∈Rl×q,θd=col(Dr)∈Rl×m

(13)

(14)

式中：函数col(·)为转置函数，具体如下：

(15)

xc,k+1=Acxc,k+Bcek

(16)

uc,k=Ccxc,k+Dcek

(17)

此外，值得注意的是，PI或PID控制器也可以被写成离散时间状态空间形式，且同样是可镇定和可观测的。考虑匹配到工业实际，式(1)中的D在本文中假设为0。但是当D≠0时，也可以容易地获得类似的结论。基于图2，从外部信号dk，ωk和rk到ek和uk的闭环动态具有如下状态空间表述：

(18)

(19)

为了提高系统的鲁棒性，需要考虑将未知干扰对跟踪误差ek和控制信号uk的影响最小化。因此，为优化问题选择以下成本函数J，优化问题成为约束下的成本函数最小化问题。即：

(20)

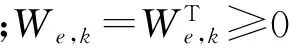
(21)

式(21)表明θ的搜索规律：

(22)

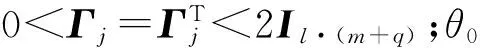
(23)

式中：α为正的常数。βj具体如下：

(24)

引理3：假设图2中的参数化实现方案具有控制对象和基于观测器的残差信号生

(25)

(26)

(27)

(28)

现证明引理3如下：根据残差信号r到u和e的传递函数矩阵，即式(17)和式(18)，证明是直接的计算，故可省略，而仅需要讨论AG的稳定性。假设标称受控对象G(z)和标称控制器K(z)如式(1),式(15)和式(16)是可镇定和可观测的，则图1的标准闭环反馈控制系统具有的内部稳定性意味着从外部信号dk，ωk，rk到ek和up,k的闭环动态是稳定的，即以下系统是稳定的：

(29)

(30)

(31)

综上，可以给出在线配置参数化矩阵Q(z)的算法流程图,如图3所示。

3 试验验证

为了验证前述所设计的自动控制系统在线优化策略实际应用的效果，基于一个无刷直流电动机测试平台控制系统进行工程化验证。图4为由2台无刷直流电动机为主体构成的无刷直流电动机测试平台，此外还有转矩测量传感器、电机驱动器和一些外围电路。控制核心算法是基于实时仿真系统和MATLAB/Simulink平台实现，其中Q(z)的优化配置算法由主机实现，具体如图5所示。

图5 基于实时仿真平台的控制策略实施

在试验时，控制目的是尽量减少负载转矩和故障对控制器的影响，电机的参考转速为3000r/min。首先，Q(z)为0，设置成本函数的权重因子等于单位矩阵，负载转矩波形为方波，第一次加载时间为11 s至16 s，然后停止5 s，反复直至第56 s。此外，在第3 000个采样点时设置一个故障，具体是通过在控制系统中增加比例增益来模拟。图6为试验中残差信号波形。图7为电机转速试验波形，包含了负载动态和故障。图8为试验中对应成本函数J和Q(z)的变化波形。从试验结果可以看出，采用在线优化后，原控制系统的鲁棒性明显增强，尤其转速跟踪抗扰性明显增强。

图6 残差信号试验波形

(a) 转速波形

(b) 转矩波形

图7转速和转矩试验波形

(a) 成本函数

(b) Q(z)

图8成本函数和Q(z)波形

4 结 语

围绕工业过程监控系统的优化控制问题，本文基于Youla参数化研究，设计了一种替代参数化实现，其结构上无需修改预先设计的控制系统而改进控制抗扰性。通过理论分析和实验研究，现总结主要结论和进一步研究方向如下：

1) 通过将在线优化控制策略应用到无刷直流电动机测试平台控制系统，验证了其有效性。

2) 新型实时优化控制的方法具有一般性，可推广到更为广泛的应用场合，如工厂的工业自动化控制系统中。

3) 实验结果表明，闭环系统鲁棒性随着每次迭代运算显著地改善。

4) 参数化矩阵动态部分的在线优化配置中极点位置将对实际效果产生较大影响。故进一步研究方向是研究存在动态的参数化矩阵在线优化问题。

[1] 范家璐，姜艺，柴天佑．无线网络环境下工业过程运行反馈控制方法[J]．自动化学报，2016，42(8)：1166-1174．

[2] 杨英杰，杨帆，曾庆喜，等．基于VC++的无刷直流电机负载特性可视化模拟测量平台研究[J]．计算机测量与控制，2015，23(4)：1141-1143．

[3] 乔维德．基于模糊PI控制的BLDCM直接转矩控制[J]．微特电机，2015，43(11)：60-63．

[4] 吕刚，张慧，王娜，等．新型能量回馈式异步电机测试系统研究[J]．电气传动，2016，46(10)：68-71．

[5] 刘昕彤, 王红艳，张冬梅，等．无刷直流电机在转子偏心故障时的容错控制研究[J]．电机与控制应用，2017，44(5)：121-127．

[6] DING S X,YANG G,ZHANG P,et al.Feedback control structures, embedded residual signals, and feedback control schemes with an integrated residual access[J].IEEE Transactions on Control Systems Technology,2010,18(2):352-367.

[7] 王立敏，周东华，朱城杰．间歇过程复合迭代学习容错保性能控制器设计[J]．上海交通大学学报，2015，49(6)：743-750．

[8] 程启明，黄伟，程尹曼，等．双级矩阵变换器驱动永磁同步电机的混合非线性控制系统[J]. 电工技术学报，2017，32(4)：101-111．

[9] 刘斌，贾蓉，何召华，等．自适应的时变比例增益的预测PID控制器[J]．控制工程，2013，20(3)：431-435．

[10] YIN S,LUO H,DING S X.Real-time implementation of fault-tolerant control systems with performance optimization[J].IEEE Transactions on Industrial Electronics,2013,61(5):2402-2411.

[11] ZHANG Y,YANG Y,DING S X,et al.Data-driven design and optimization of feedback control systems for industrial applications[J].IEEE Transactions on Industrial Electronics,2014,61(11):6409-6417.

[12] 杨承志，王宏．基于Youla参数化的动态随机系统最小误差熵控制[J]．控制工程，2007，14(4)：362-365．

[13] 马广富，杨志红，胡庆雷．基于有限维Youla参数化的多目标 H2/H∞最优控制[J]．电机与控制学报，2004，8(4)：345-349．

[14] GEORGIOU T,T,SMITH,et al.Optimal robustness in the gap metric[J].Automatic Control IEEE Transactions on, 1990, 35(6):673-686.

[15] DING S X,YANG Y,ZHANG Y,et al.Data-driven realizations of kernel and image representations and their application to fault detection and control system design[J].Automatica,2014,50(10):2615-2623.

[16] MANDIC D P,HANNA A I,RAZAZ M.A normalized gradient descent algorithm for nonlinear adaptive filters using a gradient adaptive step size[J].IEEE Signal Processing Letters,2001,8(11):295-297.