步进电动机SPWM微步距细分控制的研究

赵 涛，季宁一，刘汉忠，沈维健

(1.南京工程学院，南京 211167；2.南瑞集团有限公司国网电科院有限公司，南京 210003)

0 引 言

步进电动机具有控制简单、无积累误差等优点[1]，在数控系统、伺服控制系统、机器人终端定位及计算机外围设备等领域广泛应用[2-3]。由于步进电动机低速时存在转动振动、明显的步进现象、转速不够平稳以及运行时易发生振荡[5]等问题，限制了步进电动机在一些高性能、高精度场合的应用。为了解决上述问题，国内外学者进行了深入的研究，在控制系统、控制策略等方面提出了很多解决方案。目前应用最多的是采用微步距控制的细分驱动技术[4-6]。 其中的一种方案是以单片机通过专用集成芯片来控制其脉冲输出频率和脉冲输出数，实现步进电动机的速度控制和位置定位[5-6]。随着电子技术的发展，高性能的微处理器MCU及数字信号处理芯片DSP性能越来越好，价格也越来越便宜。相对于专用步进电动机微步控制芯片，采用MCU、DSP具有控制灵活，驱动功率范围大等特点，同时也更方便实施较为复杂的控制策略，以获得较好的控制效果[7]。因此，利用高性能MCU、DSP直接实现步进电动机微细分控制的应用受到广泛的重视。

本文以二相混合式步进电动机为控制对象，在研究二相混合式步进电动机SPWM微步距细分控制原理的基础上，对步进电动机细分驱动时的电磁转矩进行深入的分析，对基于高性能MCU的SPWM细分控制系统进行了设计。

1 SPWM细分原理及电磁转矩分析

1.1 SPWM微步距细分原理

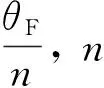
根据文献[1]，二相混合式步进电动机的电磁转矩方程可表示：

Te=-pψM[iAsin(pθ)+iBcos(pθ)]-Tdmsin(2pθ)

(1)

式中:选取转子的N极对准A轴时为转子参考位置，此时转子角度θ=0°；Tdm为磁极之间的磁通对转子影响产生的定位转矩；ψM为磁链；p为磁极齿数，其可由式(2)表示：

(2)

式中：m为电机的相数。

如果忽略定位转矩，步进电动机工作在整步驱动时，每个步距角θF对应90°电角度，则式(1)可以表示为：

Te=pψM(iAsinθE+iBcosθE)

(3)

式中:θE为转子的电角度。

当步进电动机工作在SPWM细分时，对于二相步进电动机， 细分驱动时A,B相电流可以表示为：

(4)

1.2 SPWM细分驱动电磁转矩分析

根据式(3)和式(4)可推出SPWM微步距细分驱动时(细分数n为任意值)的电磁转矩表达式:

Te=pψMIsin(θE-θk)=TMsin(θE-θk)

(5)

由式(5)可得到细分数n为不同值时步进电动机电磁转矩Te随转子电角度θE变化的曲线。图1给出了基于Mathcad的细分数n在不同值时电机的电磁转矩与最大电磁转矩TM随旋转角度的变化曲线。

图1 电磁转矩变化曲线

对式(5)进行积分，可得到90°电角度范围内电机总有效转矩表达式：

(6)

为了进一步分析在不同细分数时转矩变化的情况，根据文献[8]的总有效转矩方差：

(7)

根据式(6)、式(7)，给出了细分驱动和整步驱动总有效转矩比及方差随不同细分数变化的曲线，如图2所示。

图2 细分驱动时转矩随细分数变化规律

由图1和图2 可知， 在细分数较大时， 细分工作方式可使步进电动机的总有效转矩显著增加，步进电动机细分工作时比整步工作时转矩的波动幅度也明显减小，当n≥8时，电机的电磁转矩近似恒定，步进电动机总有效电磁转矩的方差接近于 0；此外， 随着细分数的增加，电磁转矩波动的幅度减小，波动的频率增加，细分控制可以有效地改善步进电动机的性能，但还有其它如齿槽、铁心等因素及结构和安装等问题都会对电机性能产生重要的影响。此外，当细分数较大时再提高细分数，对电机性能提升效果也不显著，同时在高速高细分的情况下器件的开关频率高，开关器件损耗也变大。

2 SPWM细分控制系统设计

2.1 系统结构

图3给出了步进电动机SPWM细分控制系统框图。直流电源经过2个全桥PWM变换器分别控制电机的二相绕组，控制系统接收给定的控制信号，根据SPWM细分微步距控制器产生对应的SPWM信号，从而控制全桥PWM变换器达到控制电机的目的。全桥PWM变换器采取双极性和单极性控制方式，通过对电机绕组电流进行快衰减、慢衰减及混合衰减的控制，可以使步进电动机定子绕组电流正弦度更好[2,5]。

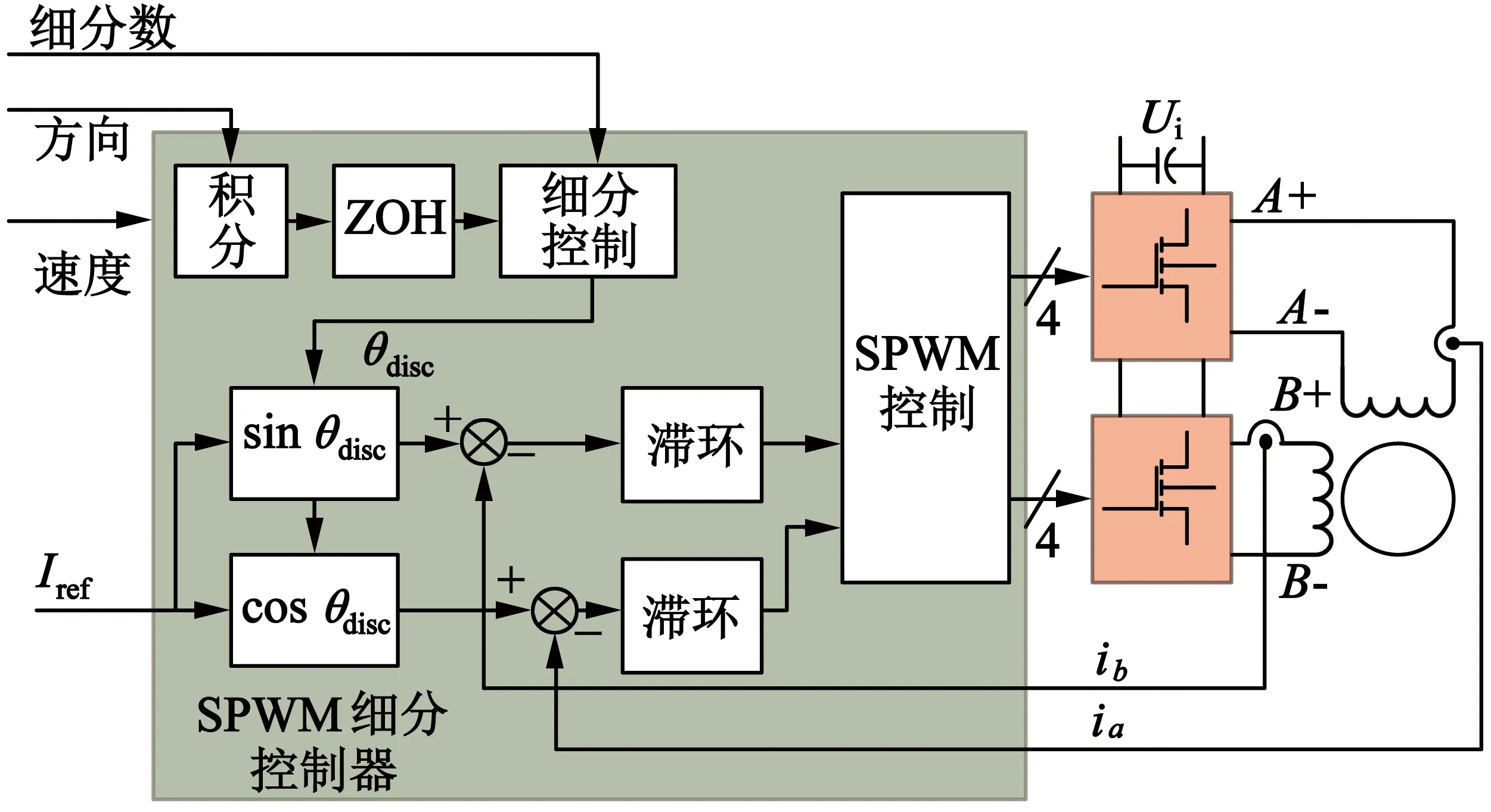
图3 步进电动机SPWM控制系统框图

2.2 SPWM细分控制策略

步进电动机每相绕组通过SPWM 脉冲， 进行正弦脉宽调制，可以对步进电动机步距角进行任意的细分。二相混合式步进电动机SPWM细分驱动的关键就是控制电机二相绕组的电流，使其为正弦规律的阶梯波，阶梯数越多则细分数越高，频率越大则电机转速越高。

首先根据最大细分数N确定对应的正弦、余弦表，根据方向设定细分数n，由式(8)可以得到下一步的指针P(k+1) ：

(8)

式中：N为n的2的倍数，P(k+1)不大于N，根据指针查表得出对应的sinθk+1和cosθk+1值。

式(4)在这里可以变换:

(9)

根据式(9)可以得到下一步细分所需要的A,B两相电流值。该值和电机电流，经过滞环比较控制，输入到SPWM发生器，输出SPWM控制脉冲。根据速度指令设置定时器的时间常数，控制每个阶梯波的作用时间，即可控制正弦阶梯数的频率，从而控制电机的转速。

3 仿真与实验研究

按照图3给出的结构框图，基于MATLAB/Simlink建立了步进电动机微步距控制的仿真模型，并采用32位单片机STM32F103设计了步进电动机SPWM细分驱动系统。本文的仿真建模及实验波形是以二相混合式步进电动机57H56605为对象，表1给出了步进电动机的主要参数。

表1 步进电动机参数

在细分数变化的情况下步进电动机A,B相的电流波形和电机旋转角度的仿真波形如图4所示。图4中电机转速为1 000 步/秒，先以n=4微步距运行，0.1 s后以n=16微步距运行。如果要保证电机转速不变，细分数增加，则换步的时间变小。当细分数较小时步进电动机存在步进现象，步距角较大，低速转动时产生振动，转速不够平稳；细分数n=16时，A,B相电流波形正弦度较好，转子位置波形平滑，实现微步转动。在细分数变化过程中，电机绕组电流变化也比较平滑。

图4 不同细分时的仿真波形

图5给出了细分数n=16时，电机正转变为反转时的电流和旋转角度的仿真波形。电机一开始正转，0.1 s后方向控制信号由1变为-1，电机反转；反转时B相电流由滞后A相电流90°变为超前A相电流90°。在正反转切换过程中，电流变化平稳，电机转速没有出现过冲；在0.2 s电机转角回原位。

图5 正、反转运行时的仿真波形

图6给出了在不同细分数下，步进电动机定子绕组电流的实验波形，电流波形通过电流探头获取。从图6中可以看出，步进电动机工作在8细分时， 电流波形已经趋近正弦波，但还存在较明显的台阶，电流正弦度不够好，其合成磁场是多边形，电机运行还存在步进现象。随着细分数增加，A,B相电流也越接近正弦波；在步进电动机细分数n=128时，定子绕组电流波形正弦度好，A,B相电流的相位也保持稳定，说明系统对电流的控制效果较好。电机绕组受到正弦与余弦电流的激励，磁场圆形度好，电机运行平稳。在电机起动时，可以让电机以高细分数运行，再按照梯形、S形加速，逐渐减少细分数，这样在相同的换步时间下，细分数少，电机转速高。

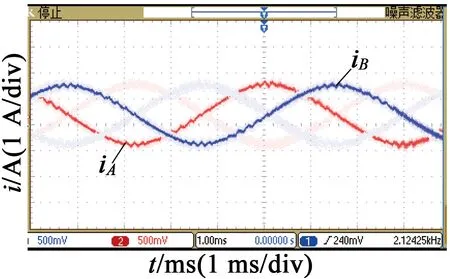
(a) 细分数n=8

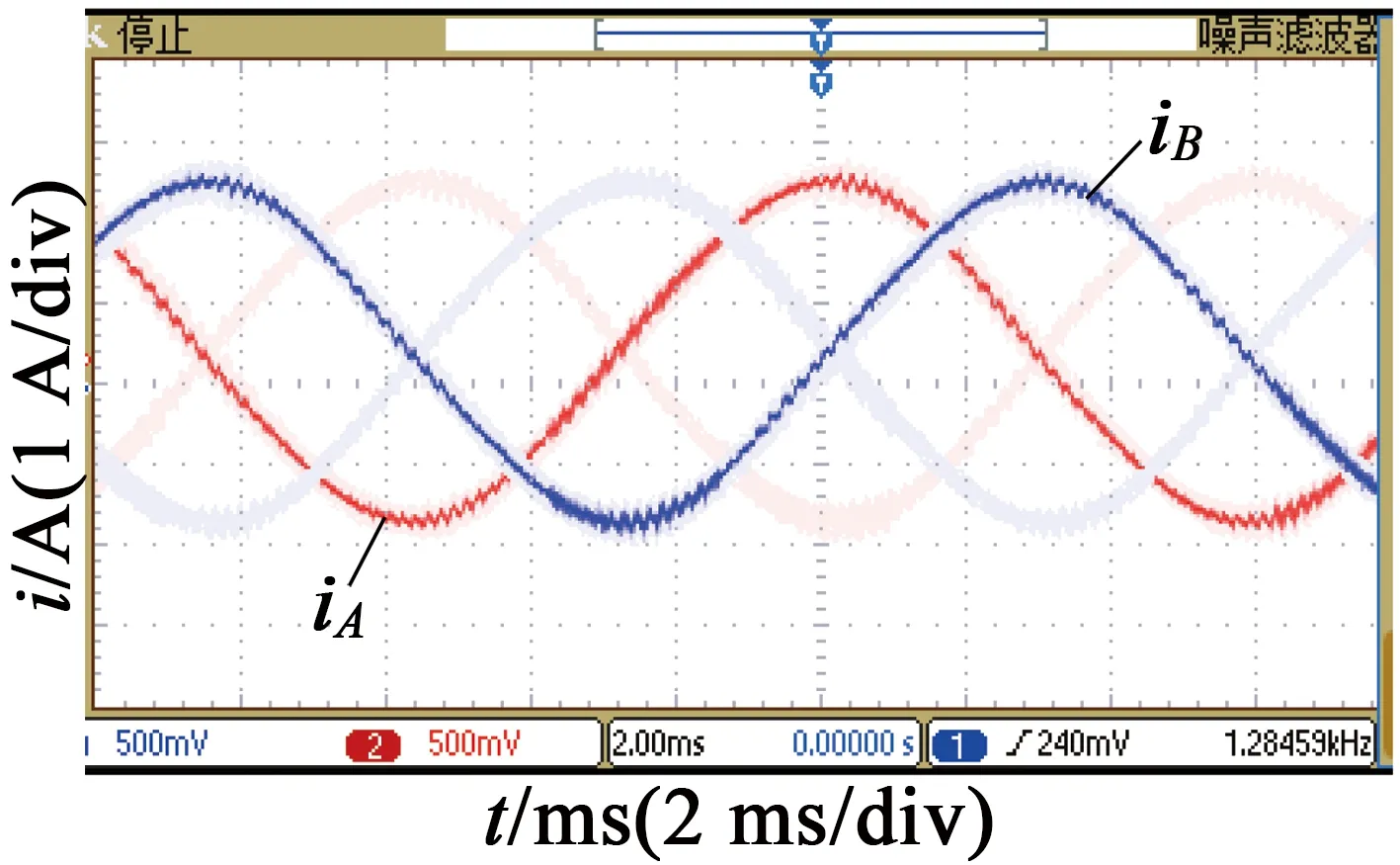
(b) 细分数n=16

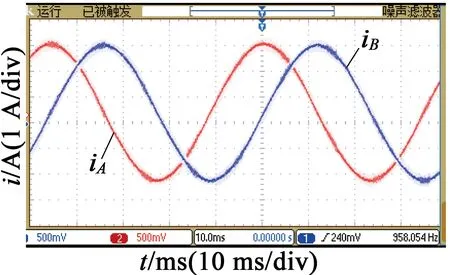
(c) 细分数n=128

SPWM细分控制可使电流变化趋缓，通过对电流的控制达到对电机运行状态的控制，使得电机运行时噪声降低，同时由于步距角降低，在高细分数时电机的扭矩也得到增强，带负载能力得到了提升。此外，该系统的硬件结构简单，开展功能多，成本较低，细分精度高，可以灵活控制步进电动机的细分数。

4 结 语

本文对SPWM细分微步距驱动时步进电动机的电磁转矩进行了分析，从理论上阐述了采用SPWM细分可使步进电动机有效电磁转矩增加、电磁转矩波动幅度减小，采用SPWM细分能够有效地克服步进电动机低频振荡、高频失步等缺点，提高步进电动机的运行性能。在此基础上，对基于MCU的步进电动机SPWM细分微步距控制系统进行了研究和实现。仿真和实验表明，该系统细分的切换容易，步进电动机定子绕组流正弦度好，改善了步进电动机的步进现象，达到了微步距转动、运转平稳的目的。

[1] ACARNLEY P.Stepping motors-a guide to theory and practice,4th edition[M].LondonL:The Institution of ElectricalEngineers,2002.

[2] 郑雪钦，郭东辉.基于混合模式PWM二相步进电机驱动控制的研究[J].系统仿真学报，2012，24(2):456-461.

[3] 赵涛.基于CAN总线太阳能电池自动跟踪控制器的设计[J].制造业自动化，2012(12):105-108.

[4] 杨 斐， 刘景林， 董亮辉.两相混合式步进电动机动态多细分驱动器设计[J].微特电机，2013，41(2):42-44,47.

[5] GAAN D R,KUMAR M,SUDHAKAR S.Frequency modulation based microstepping of stepper motor for real time position tracking applications[C]//IEEE International Conference on Power Electronics,Drives and Energy Systems.IEEE,2017:1- 6.

[6] 田云， 张宏龙.基于SA4828的三相步进电动机细分驱动[J].微特电机，2013，41(7):63-66.

[7] 顾凤香, 黄云龙, 陈国定.基于TMS320F2812的步进电动机任意可变细分控制系统研究[J].微电机，2009,42(5):28-30.

[8] 李茂军， 刘鼎邦.步进电机细分驱动电磁转矩分析[J].控制工程，2013,20(2):243-245.