电流-位置神经网络模型的构建与SRM转矩控制

党选举，陈恩普，姜 辉，伍锡如，彭慧敏

(桂林电子科技大学，桂林 541004)

0 引 言

开关磁阻电动机(以下简称SRM)具有成本低、结构简单、维护方便以及可靠性高等优点，适合用于新能源电动汽车动力系统[1-3]。然而，由于SRM的双凸极结构以及开关式的控制方式，导致其电磁特性的高度非线性和强耦合性，造成SRM运行时尤其是低速运行时存在转矩脉动较大的问题。动力系统转矩脉动会导致车辆的噪声问题以及特定频率下的谐振问题，这些缺点阻碍了SRM在小型电动汽车上的应用。目前，抑制转矩脉动主要方法有两类：一类是从电机设计的角度，改进电机的结构；另一类是从控制策略的角度，设计更合适的控制方案[4]。在改进电机结构方面，文献[5]考虑到两相SRM转矩死区导致的转矩脉动，提出了一种两相4/3极电机结构克服此问题；文献[6]提出一种在转子齿两侧开槽的方法，改变电机磁场分布，达到抑制SRM转矩的目的。在控制策略方面，改进的转矩分配函数(以下简称TSF)控制应用广泛[7-9]，文献[7]考虑到SRM的强非线性，舍弃固定的TSF，以相电流平方最小为目标不断优化TSF函数；文献[8]考虑到电机磁场高度磁饱和性，提出了一种优化相电流曲线的方法，降低了转矩脉动，同时减小了换相时的功率损耗；文献[9]采用模糊逻辑控制不断调整TSF，以抵消拖尾电流的影响，从而降低转矩脉动。

文献[7-9]中的TSF控制均有参考相转矩转换成相电流的环节，本质上是对电流的分配。转矩-电流转换有两种方法：一种方法是查表法，但是表格不易获取且占用大量系统资源；另一种是数学计算的方法，通常计算复杂或者结果不精确。文献[10]采用交流电动机坐标变换的方法，将SRM的给定电流进行坐标变换，然后再进行一系列复杂的数学运算，可以获得SRM各相的参考控制电流。

本文借鉴文献[10]中不经过转矩-电流转换而直接获取参考相电流的方法，考虑到SRM运行时相电流平方之和与转子位置角的周期性关系，提出了电流-位置神经网络模型，直接由转子位置角计算相电流平方之和。参考TSF控制的分配方法，设计电流分配函数计算参考相电流。仿真结果表明，本文的方案能有效地降低SRM转矩脉动。

1 电流-位置模型构建

1.1 基于电流-位置神经网络模型的控制系统

SRM传统TSF控制框图如图1(a)所示。期望转矩通过转矩分配得到各相的参考转矩，参考转矩经过转矩-电流转换得到各相参考电流，再通过电流滞环控制功率变换器件通断进而驱动电机。

由于SRM非线性严重，无法用解析方法表示转矩-电流模型[10]，TSF控制通常采用简化的线性转矩-电流模型计算参考相电流[11]，但简化模型不能精确描述电机转矩与电流的关系，导致控制系统不能得到准确的参考相电流。为了解决此问题，该文从电流-位置的关系出发，提出了基于电流-位置神经网络模型的控制系统，整体框图如图1(b)所示。相电流平方之和由电流-位置神经网络模型得到，其分配后得到各相参考电流，再通过电流滞环控制功率变换器件通断进而驱动电机。

(a) 传统TSF控制框图

(b) 基于电流-位置神经网络模型的控制框图

1.2 相电流平方之和与转矩的关系

SRM磁通遵循沿着磁阻最小路径闭合的原理，产生磁拉力形式转矩，转矩的大小与相电感、相电流和转子位置角有关，SRM电磁转矩的数学模型可简化[12]：

(1)

式中：Tk为k相电磁转矩的值；Lk为k相电感的值；ik为k相电流的值；θ为电机转子位置角。

选择合适的开通关断角，在SRM磁路未达到饱和时，相电感与转子位置角近似为线性关系[13]，电感变化率可近似为常数K。式(1)可以写成：

(2)

即：

(3)

式(2)和式(3)中:T为SRM的输出电磁转矩。

由式(3)可知，相电流平方之和与输出电磁转矩有线性对应关系。

1.3 电流-位置神经网络模型构建

以SRM某相导通至其邻相导通为一个运行区间，将电机划分为不同的运行区间。如图2所示，θ1～θ2为一个运行区间，θ2～θ3为下一个运行区间。

图2 运行区间划分示意图

SRM不同区间运行状态相同只是通断的相不同，也就是说各个区间相电流波形是相同的。因此，SRM运行时相电流平方之和I2与转子位置角θ呈周期函数关系。

实现文献[14]提出的算法，得到如图3所示的12/8极SRMθ-I2图。图3中各周期的波形与高斯函数接近，验证了相电流平方之和与转子位置角呈周期性关系。

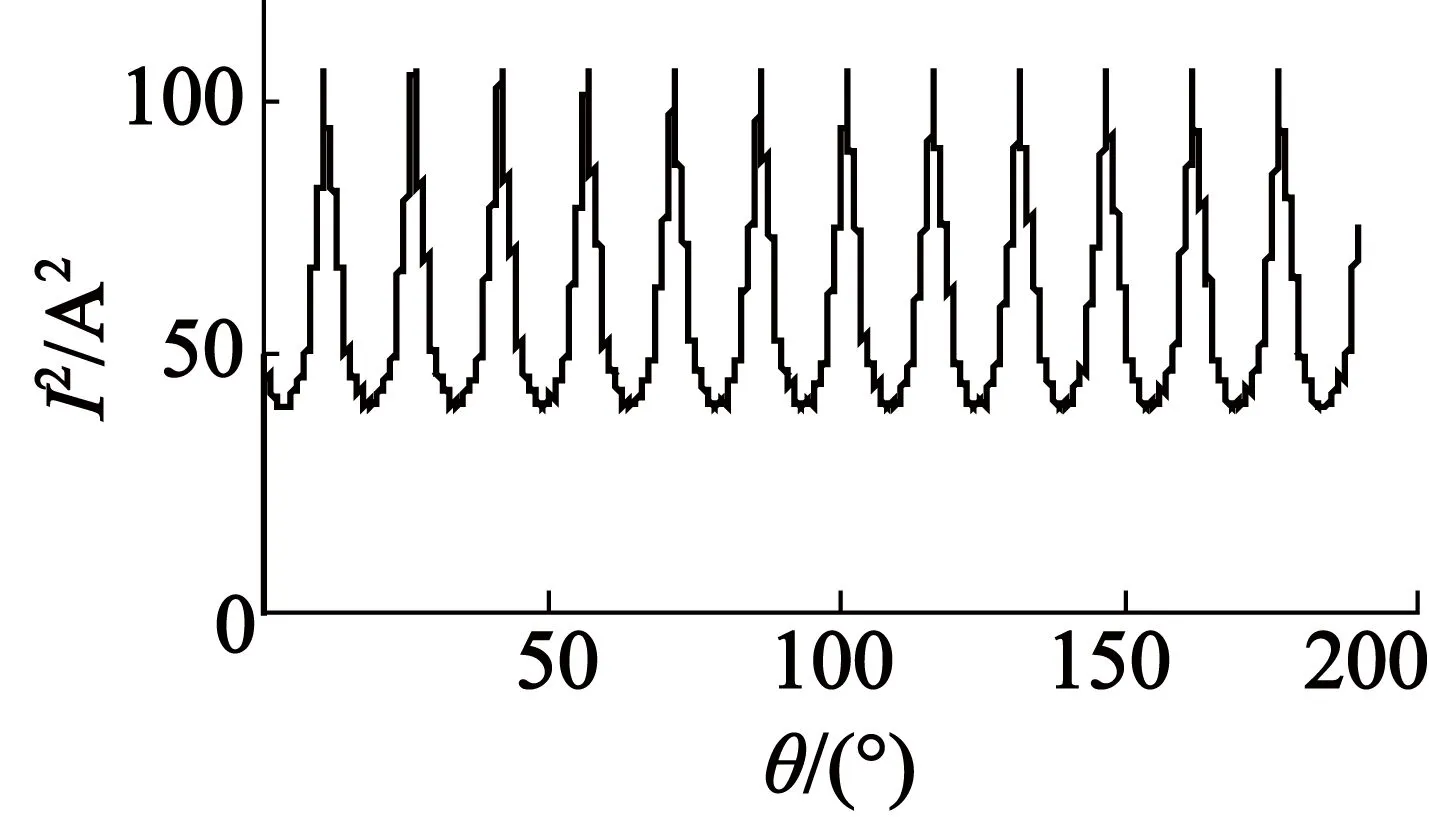
图3 文献[14]控制方法θ-I2关系

利用相电流平方之和与转子位置角所表现出的周期关系，构建电流-位置神经网络模型。由式(3)可知，在电流-位置神经网络模型中，可以直接采用转矩偏差学习得到相电流平方之和。为提高计算速度并减小计算量，根据图3中各周期的波形与高斯函数接近的特点，神经网络的激励函数选用高斯基函数。电流-位置神经网络模型的实现原理如图4所示。

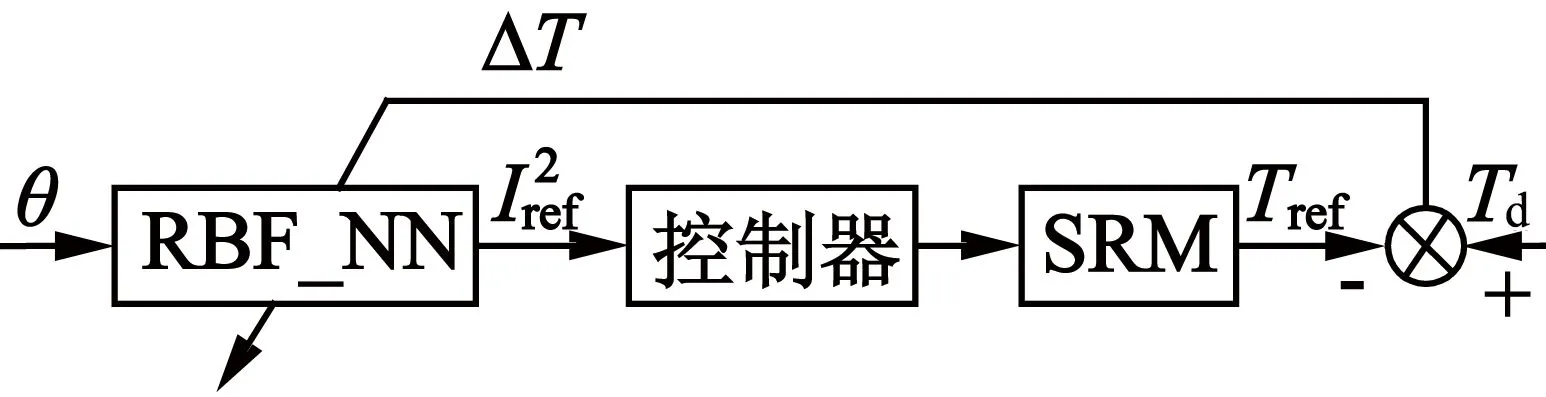
图4 电流-位置神经网络模型的实现原理

图4中，电流-位置模型输出的相电流平方之和通过控制器转换为控制信号来控制SRM；期望转矩与参考电磁转矩之差作为误差信号来学习神经网络。

图5为电流-位置RBF(高斯函数)神经网络模型的拓扑结构。

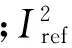
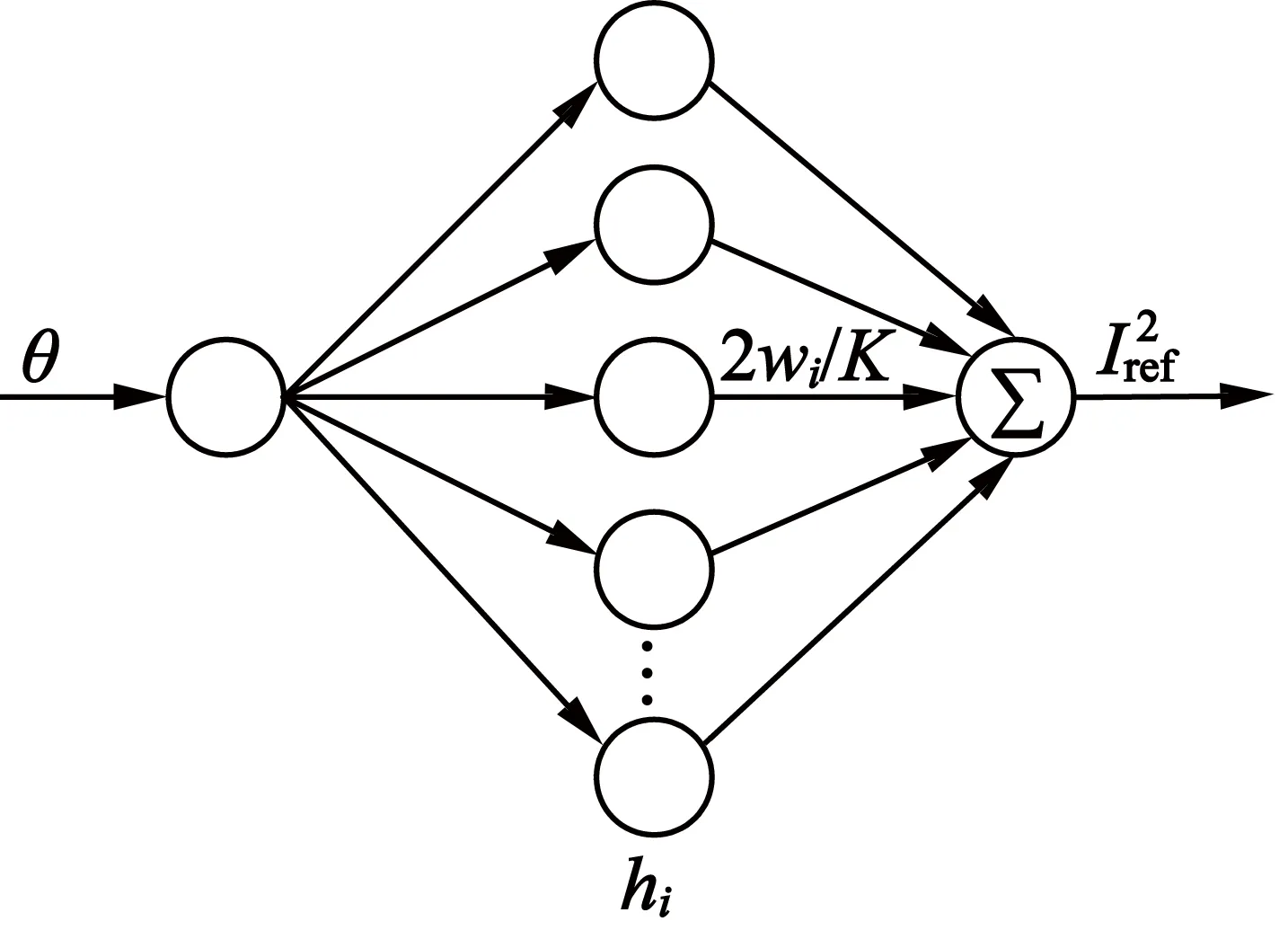
图5 神经网络拓扑结构

图5神经网络中各参数间关系如下：

(4)

(5)

式中：ci为节点的中心；bi为节点的基参数。

误差定义：

(6)

式中：Td为期望转矩;Tref为参考电磁转矩;T为SRM的输出电磁转矩。

根据梯度下降法，权值、节点中心及节点基宽参数的迭代算法：

ηΔT(k)hi(k)

(7)

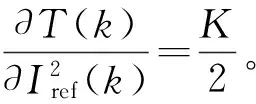
wi(k+1)=wi(k)+Δwi(k)+α[wi(k)-wi(k-1)]

(8)

(9)

bi(k+1)=bi(k)+Δbi(k)+α[bi(k)-bi(k-1)]

(10)

(11)

ci(k+1)=ci(k)+Δci(k)+α[ci(k)-ci(k-1)]

(12)

式(7)～式(12)中：η为学习速率；α为动量因子。

本文通过转矩误差学习神经网络使网络中的权值不断调整，间接使电感变化率K的值也不断调整，从而避免了因假设相电流平方之和与转矩呈线性关系给模型带来的误差。

2 电流环设计

2.1 电流分配

典型的分配函数有直线型、指数型、正弦型、立方型4种[16]。参考文献[16]，选择正弦型分配函数作为电流分配函数。正弦型电流分配函数如下：

(13)

式中：fk(θ)为第k相的电流分配函数；θon为开通角；θov为相电流重叠角；θoff为导通相电流减小的起始角；τr为周期角。

(14)

2.2 分区细化的电流滞环控制器

本文采用文献[12]提出的分区细化的电流滞环控制器。在传统电流滞环控制仅控制功率器件处于1(开)和-1(关)两种状态的基础上增加了0(续流)状态。在SRM单相导通区和开通区，当电流偏差小于阈值|ΔImax|时，开关状态为0。

3 仿真结果与分析

为了验证所提出控制方法的正确性，在MATLAB/Simulink环境下进行仿真研究。模型采用Simulink模型库中12/8极非线性SRM模型[17]。表1为电机的主要参数。

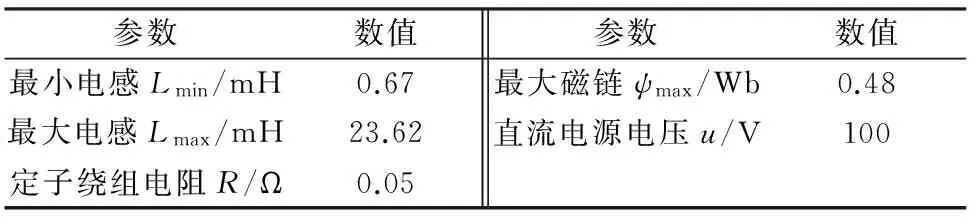
表1 电机的主要参数

为便于仿真结果的分析，将转矩脉动量化。定义转矩脉动系数Kt[18]：

(15)

式中：Tmax，Tmin，Tav分别为电机达到稳定状态后的最大电磁转矩、最小电磁转矩和平均电磁转矩。

为了验证基于电流-位置神经网络模型的控制效果，将其与SRM传统TSF控制比较，仿真实验中，期望转矩均设定为5 N·m，负载转矩为4.8 N·m。传统TSF控制仿真结果如图6所示，其稳定运行时转矩脉动系数为45.44%。基于电流-位置神经网络模型的控制方法仿真结果如图7所示，其稳定运行时转矩脉动系数为3.15%。从转矩脉动系数上看，本文的控制方法能有效地降低SRM的转矩脉动。

(a) 转矩

(b) 电流

图6Td=5 N·m时传统TSF控制的仿真情况

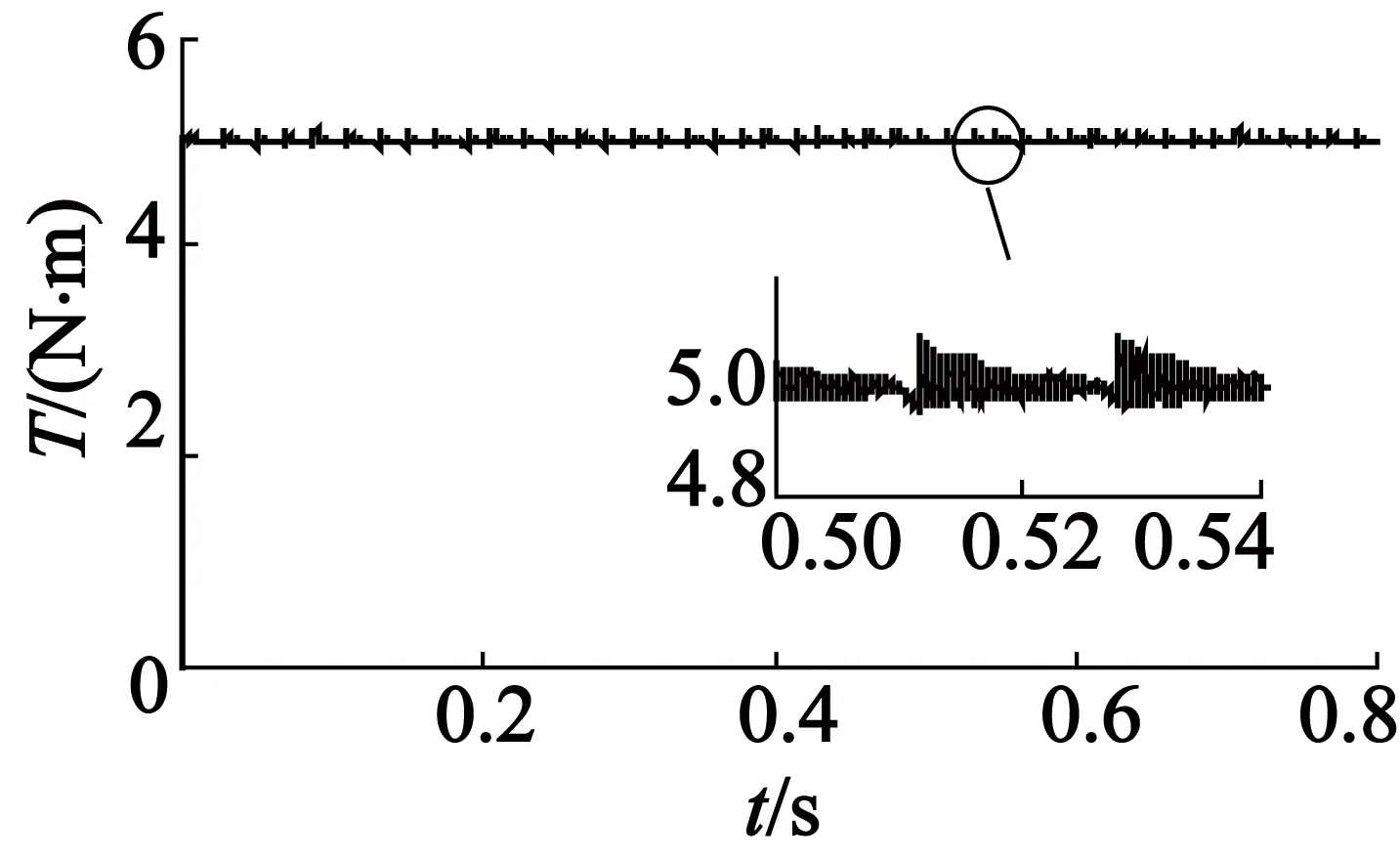
(a) 转矩

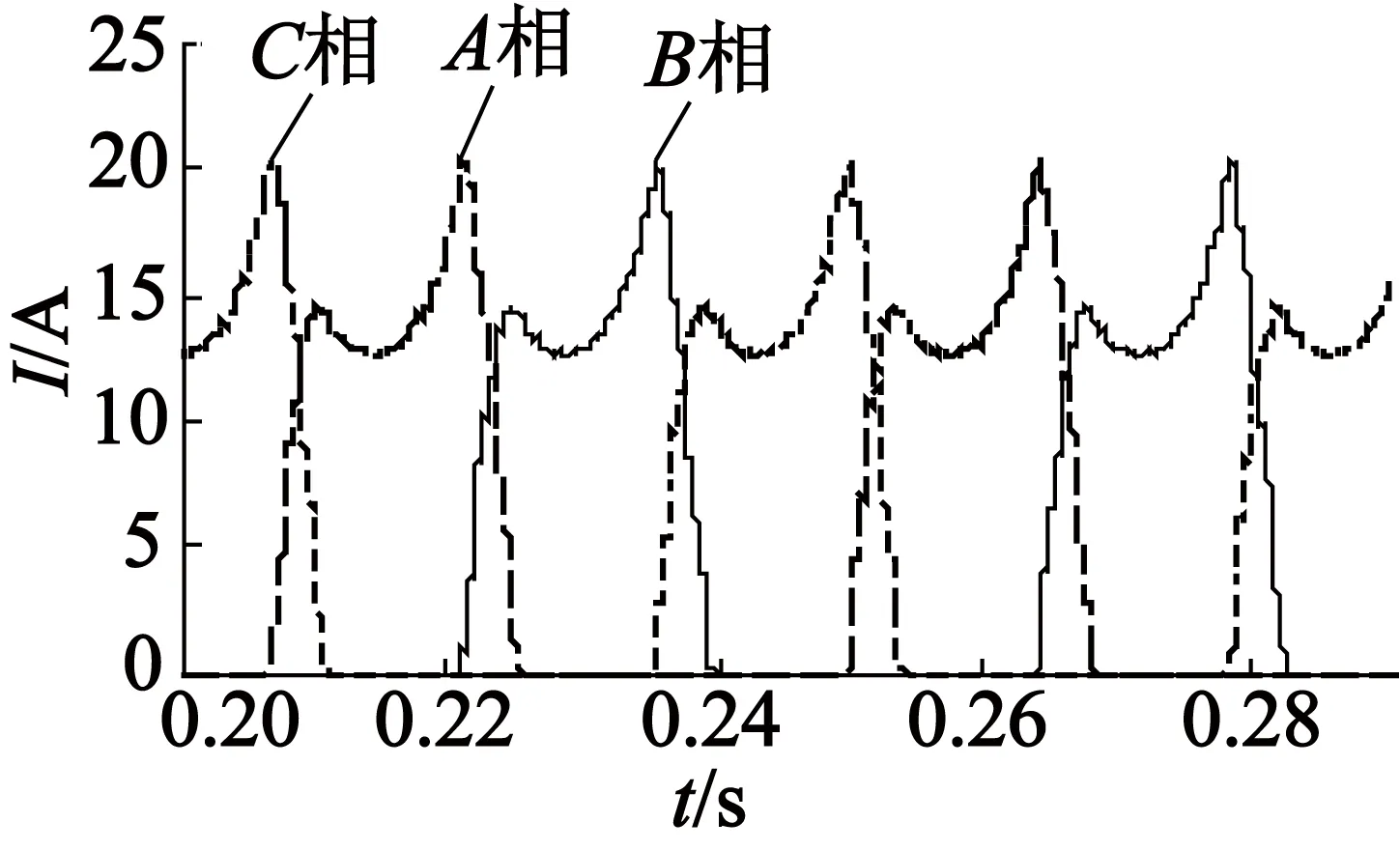
(b) 电流

图7Td=5 N·m时基于电流-位置神经网络模型的仿真情况

由于采用线性转矩-电流模型，传统TSF控制本质上是对恒定的相电流平方之和分配，所以三相电流波形为图6(b)的分配函数的波形。本文的控制方法利用了转子位置角与相电流平方之和的周期关系，优化了相电流平方之和，其分配后的波形如图7(b)所示。

为了验证算法在不同转矩下的控制效果，采用不同负载进行仿真实验。图8中，期望转矩设定为8 N·m，负载转矩为7.8 N·m，其稳定运行时转矩脉动系数为4.21%。图9中，期望转矩为10 N·m，负载转矩为9.8 N·m，其稳定运行时转矩脉动系数为3.90%。图7～图9的仿真结果结合转矩脉动系数说明，本文的控制方法适用于多种负载状况，电流波形证明所提出电流-位置神经网络模型能有效优化相电流。

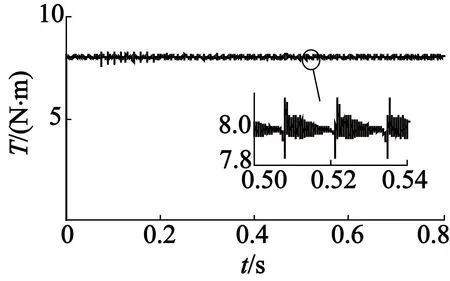
(a) 转矩

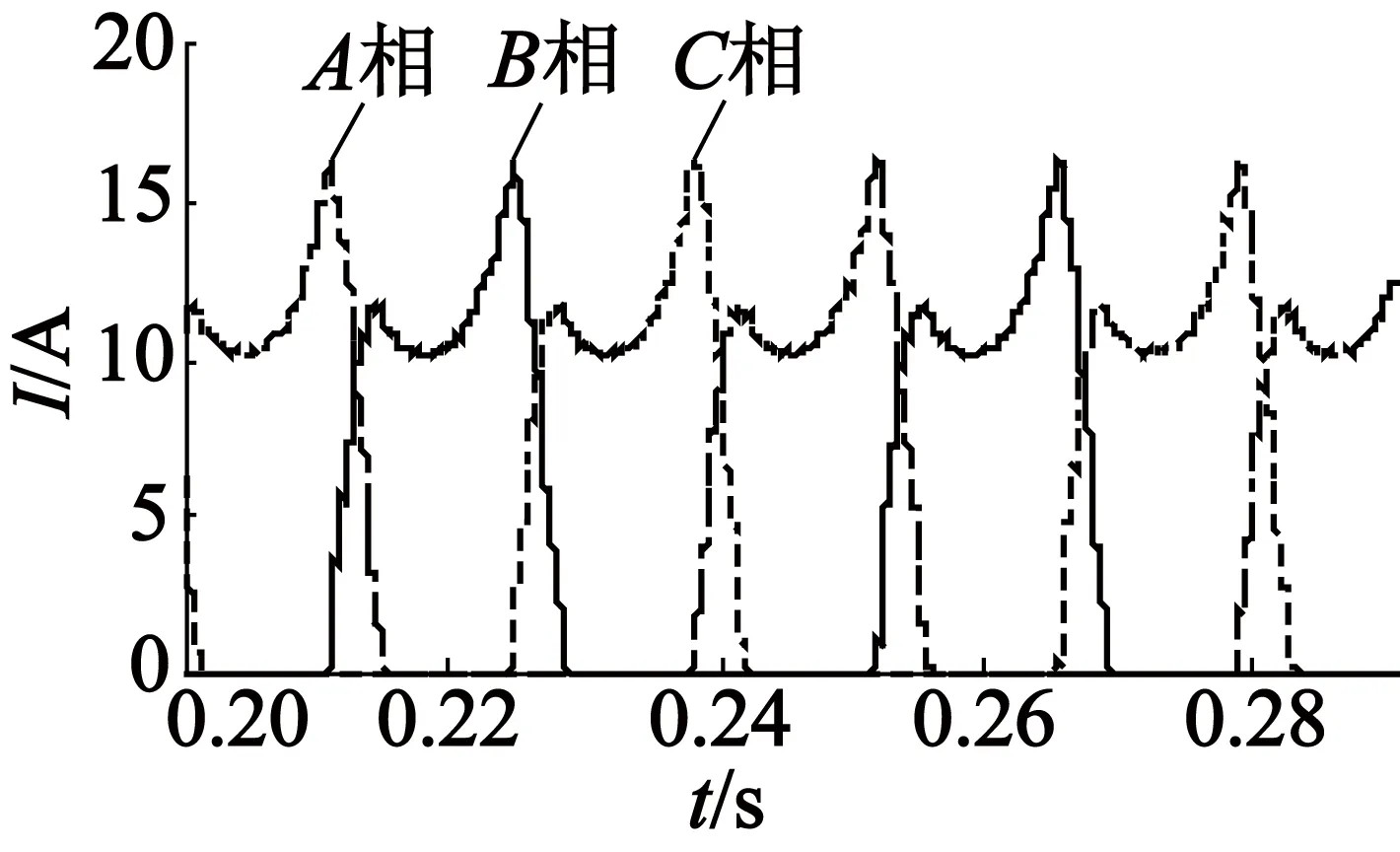
(b) 电流

图8Td=8 N·m时基于电流-位置神经网络模型的仿真情况

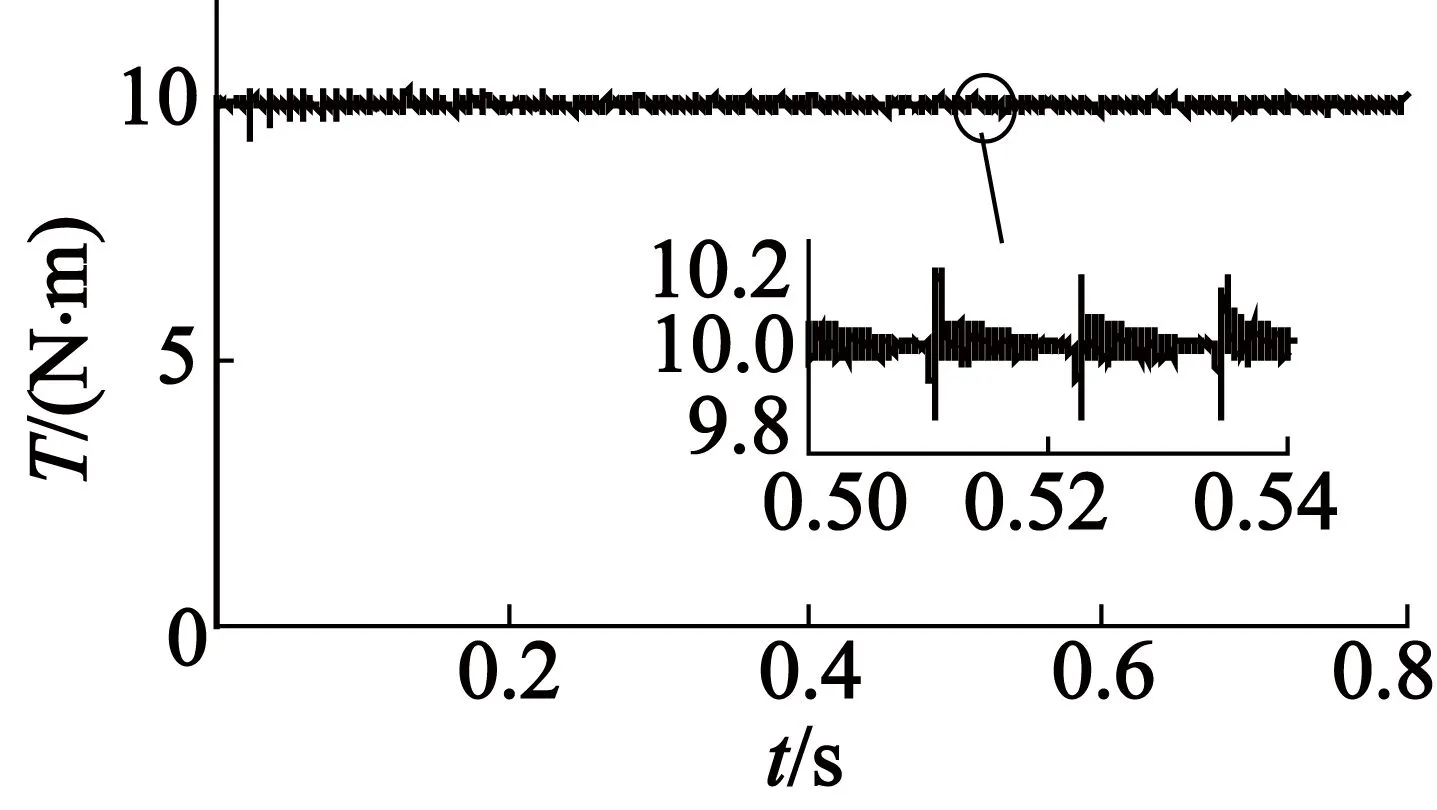
(a) 转矩

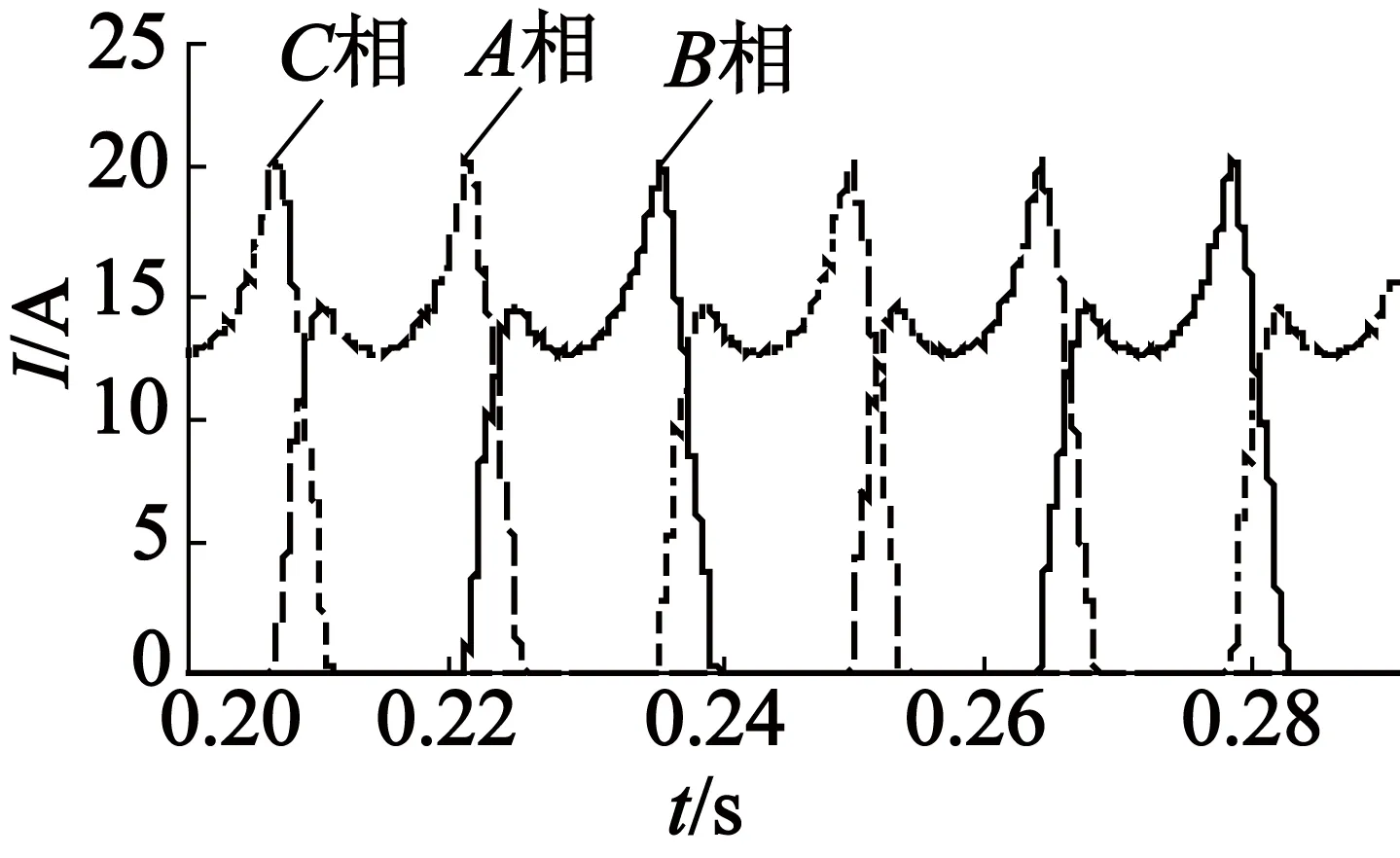
(b) 电流

图9Td=10 N·m时基于电流-位置神经网络模型的仿真情况

图10中，负载转矩为4.8 N·m，期望转矩在0.4s由5N·m突变为8N·m；0.45s突变为5N·m。仿真结果表明，输出转矩能快速地跟踪给定值，说明所设计的系统动态响应较快。

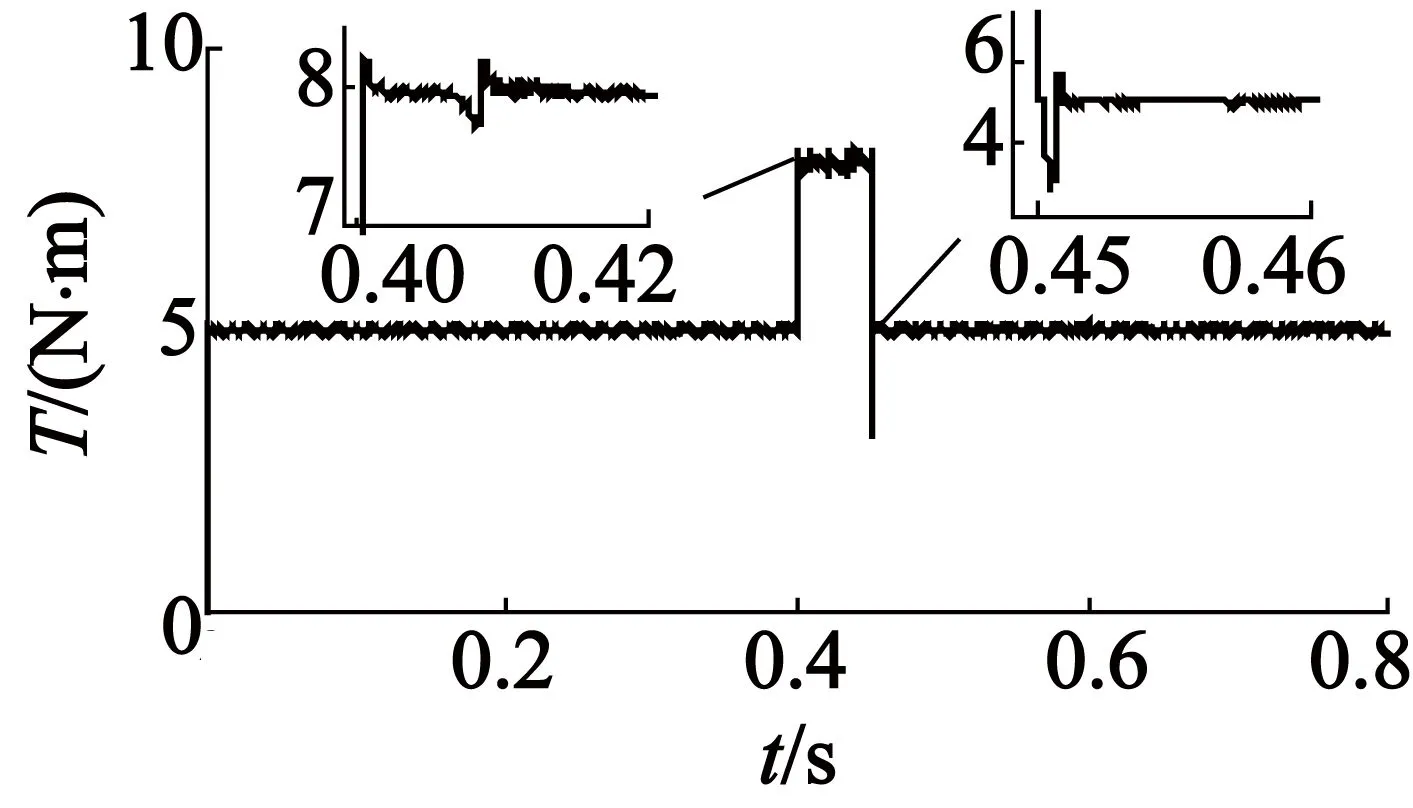
图10 SRM期望转矩阶跃变化系统响应曲线

为了检验在不同电流下的控制效果，将电感变化率近似处理为常数K。采用不同的电流值进行仿真实验，仿真结果如表2所示，电流覆盖了从10 A～40 A的范围。从表2中可知，在一定的电流范围内将电感变化率进行近似处理，对SRM控制效果的影响较小，说明了本文控制方法的有效性。

表2 基于电流-位置神经网络模型的SRM仿真结果

表2中，Td为期望转矩；TL为负载转矩；Imax为相电流最大值；Kt为转矩脉动系数。当负载转矩设定为24.8 N·m，相电流达到52 A时，电机磁路饱和，导致换相紊乱,使电机不可控。

4 结 语

本文根据SRM相电流平方之和与转子位置角所表现出的周期性关系，提出了电流-位置神经网络模型，直接由转子位置角计算相电流平方之和。再通过分配函数得到参考相电流。本方法的优势可以归纳为以下几点：

1) 控制方案中没有复杂的转矩-电流转换环节，在提升控制效果的同时，简化了控制过程，使算法具有较强的实用性。

2) 在没有利用电机模型信息的前提下，实现了SRM的有效控制，消除了控制系统设计对模型的依赖性。

3) 仿真结果显示，本方法在一定电流范围内能有效抑制SRM转矩脉动，是一种切实有效的控制方法。

[1] WANG S Y,LIU F Y,CHOU J H.Applications on adaptive recurrent cerebellar model articulation controller for switched reluctance motor drive systems[C]//2016 International Symposium on Computer,Consumer and Control (IS3C).IEEE,2016:6-9.

[2] ZHENG Q,XU J X,PANDA S K.A study on torque modelling of switched reluctance motors[C]//American Control Conference (ACC).IEEE,2013:321-326.

[3] 宋金龙,刘勇智,周政,等.中低速开关磁阻电机转矩优化策略研究[J].西安交通大学学报,2016,50(11):83-90.

[4] 漆汉宏,张婷婷,李珍国,等.基于 DITC 的开关磁阻电机转矩脉动最小化研究[J].电工技术学报,2007,22(7):136-140.

[5] PHAM T H, LEE D H, AHN J W.Design of novel high speed 2-phase 4/3 switched reluctance motor for air-blower application [C]//2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM).IEEE,2015:1520-1524.

[6] 张鑫,王秀和,杨玉波,等.基于转子齿两侧开槽的开关磁阻电机振动抑制方法研究[J].中国电机工程学报,2015,35(6):1508-1515.

[7] YE J,BILGIN B,EMADI A.An offline torque sharing function for torque ripple reduction in switched reluctance motor drives[J].IEEE Transactions on Energy Conversion,2015,30(2):726-735.

[8] DOWLATSHAHI M,NEJAD S M S,MOALLEM M,et al.Torque ripple reduction of switched reluctance motors considering copper loss minimization[C]//IEEE International Conference on Industrial Technology (ICIT).IEEE,2014:858-865.

[9] RO H S,LEE K G,LEE J S,et al.Torque ripple minimization scheme using torque sharing function based fuzzy logic control for a switched reluctance motor[J].Journal of Electrical Engineering & Technology.2015,10(1):118-127.

[10] WANG J J.A common sharing method for current and flux-linkage control of switched reluctance motor[J].Electric Power Systems Research,2016,131:19-30.

[11] SAHOO S K,PANDA S K,XU J X.Indirect torque control of switched reluctance motors using iterative learning control[J].IEEE Transactions on Power Electronics,2005,20(1):200-208.

[12] MATUTE A,VIOLA J,RESTREPO J,et al.Switched reluctance machine fuzzy modeling applied on a MRAC scheme[C] //IEEE 6th Latin American Symposium on Circuits & Systems (LASCAS).IEEE,2015:1-4.

[13] 王浩.基于电流分配方法的开关磁阻电动机速度控制[D].杭州：杭州电子科技大学,2016.

[14] 党选举,袁小唐,胡景佳.基于柔性神经网络的 SRM 直接瞬时转矩控制[J].电气传动,2014,44(5):62-66.

[15] SATO Y,MURAKAMI K,TSUBOI Y.Sensorless torque and thrust estimation of a rotational/linear two degrees-of-freedom switched reluctance motor[J].IEEE Transactions on Magnetics,2016,52(7):1-4.

[16] VRENKEN R H S,DUARTE J L,WIJNANDS C G E,et al.Switched reluctance motor drive for full electric vehicles-Part I:Analysis[C]//8th International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER).IEEE,2013:1-7.

[17] CAJANDER D,LE-HUY H.Design and optimization of a torque controller for a switched reluctance motor drive for electric vehicles by simulation[J].Mathematics and computers in simulation,2006,71(4):333-344.

[18] HUSAIN I.Minimization of torque ripple in SRM drives[J].IEEE Transactions on Industrial Electronics,2002,49(1):28-39.