基于STL模型的NURBS刀路轨迹规划算法

钱 乘，江本赤，周 辉，李 震

利用STL模型加工部件时，STL切片轮廓数据是生成刀路轨迹的基础。在CAD模型转换成STL模型时，需要把设定的弦高差作为模型转换的精度误差［1］。目前，基于STL模型的切片算法是主流的研究内容，该算法以封闭多边形表示二维封闭轮廓，而基于STL模型数控加工刀路轨迹的规划算法存在精度方面的损失，造成加工模型与CAD模型之间的误差增大。基于CAD模型的直接切片算法虽然可以提高加工精度，但需要特定的软件支持，且运算量大、效率低［2］。STL模型具有输出广泛、切片易于处理、拓扑适应能力强等优势，因此在加工一些复杂的零件时，经常采用STL模型［3］。

研究人员提出了多种基于STL模型的刀路轨迹规划算法。ZHU H等［4］利用顶点的非等距偏置性建立了偏置模型，生成了具有恒定扇贝高度的螺旋刀具路径。徐金亭等［5］利用顶点邻接三角形角度的正弦值加权计算了该顶点的单位法矢量，利用偏置距离建立了偏置模型，通过对该模型做离散处理得到了加工轨迹。该方法虽然逻辑表达简单直观，可以取得较好的计算结果，但需要通过偏移顶点对偏置模型进行计算，这会造成计算量偏大、效率偏低等后果。另外，偏置模型的精度误差也会导致加工精度的下降。LI M等［6］利用STL切片直接生成刀触点，通过刀触点计算刀位点，并对刀位点进行干涉检测处理。陈晓兵等［7］用刀触点计算了刀位点，并用最小二乘法将其拟合成NURBS刀路轨迹。赵萍等［3］对切片轮廓进行三次分段NURBS曲线插值，通过刀触点计算出刀位点，提出了数控加工路径的规划算法。虽然该算法的计算过程简单，可以得到精确的刀路轨迹，但是离散技巧的运用降低了加工精度。针对这一问题，我们提出了基于STL模型的NURBS刀路轨迹规划算法。在去除STL模型切片冗余数据的基础上，先根据预设的阈值对封闭多边形轮廓进行分段，通过NURBS曲线进行拟合，然后设定容差阈值，利用容差离散法对拟合的曲线进行离散，得到了刀触点，给出了刀路轨迹规划算法。

1 STL模型切片数据的预处理

STL模型由CAD模型表面三角化处理生成。通过对STL模型的切片处理，可获得一系列二维封闭多边形轮廓，由这些多边形轮廓生成的数据点是生成刀路轨迹的基础。

1.1 切片数据的获取

获取切片数据通常分为3步，这3步分别是分层方向的选取与分层厚度的确定、三角形与切平面交点计算、根据三角形邻接关系排序与连接交点［8］。其中分层方向一般选取与z轴平行的方向，分层厚度需要根据模型的成型精度确定。分层厚度越小，打印精度越高，但耗费的打印时间也就越长。

用一系列平行于xoy平面的切平面分割STL模型，得出切平面与相交三角形的交点，此时交点属于无序状态，需要根据三角形间的拓扑关系以逆时针或者顺时针的顺序将其排序、连接。例如，图1所示的就是简单STL模型和切片模型。

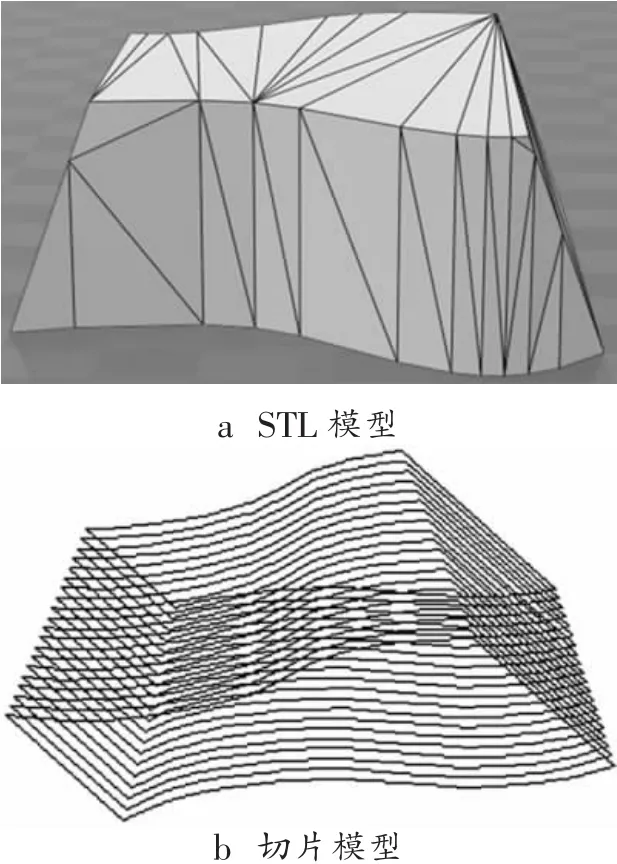
图1 STL模型与切片模型

1.2 冗余数据的删除

STL模型本身的缺陷导致了获取的切片数据存在大量的冗余交点。这些冗余交点分为两种类型，即同一交点有多个重合交点和同一直线上存在多个交点。例如，在图2所示的模型中，切平面 zi、 zi+1与STL模型相切时，从交点 P5与 P6得到的二维轮廓信息中，存在重合的交点。若 T1、 T2和 T3处于同一平面，则从得到的二维轮廓信息中，可以发现 P1和 P4可决定该线段，而P2和 P3为冗余数据点。

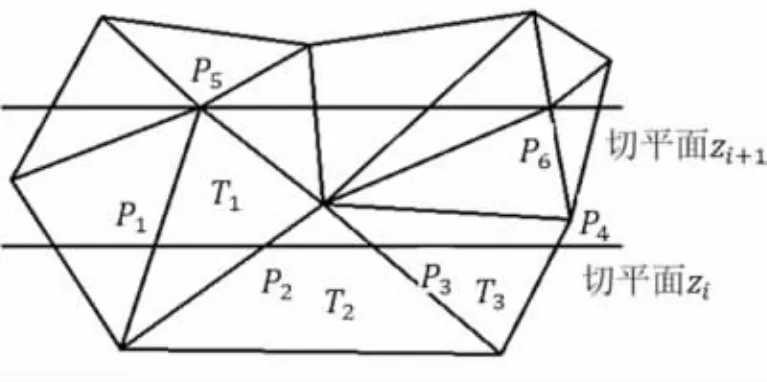
图2 冗余数据点的说明

对于同一交点有多个重合交点的情况可以进行去重处理。假设切片之后得到一系列二维轮廓数据点Pi( i = 1 ,2,… ,t )，依次按顺序从中选取3个交点 Pk−1、Pk和Pk+1(k = 2,… ,t −1)， 计算 Pk−1Pk与 PkPk+1之间的夹角 α （图3）， P0点对应的夹角可通过 Pt、 P0和 P1计算。在数据点对应的夹角中，有的夹角度数小于10-5，甚至更小。因此，需要设定一定的阈值 θ ，当 α <θ 时，就认为该数据点为同一直线上的交点，并将此点删除。例如，在图4中，图4a为切片模型某一层轮廓数据图，图4b为冗余数据点删除之后的轮廓数据图。

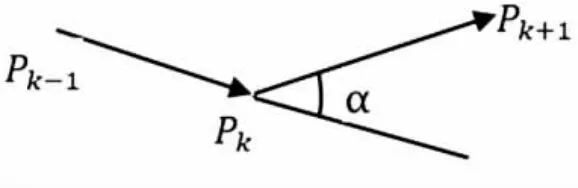
图3 Pk-1Pk与PkPk+1夹角

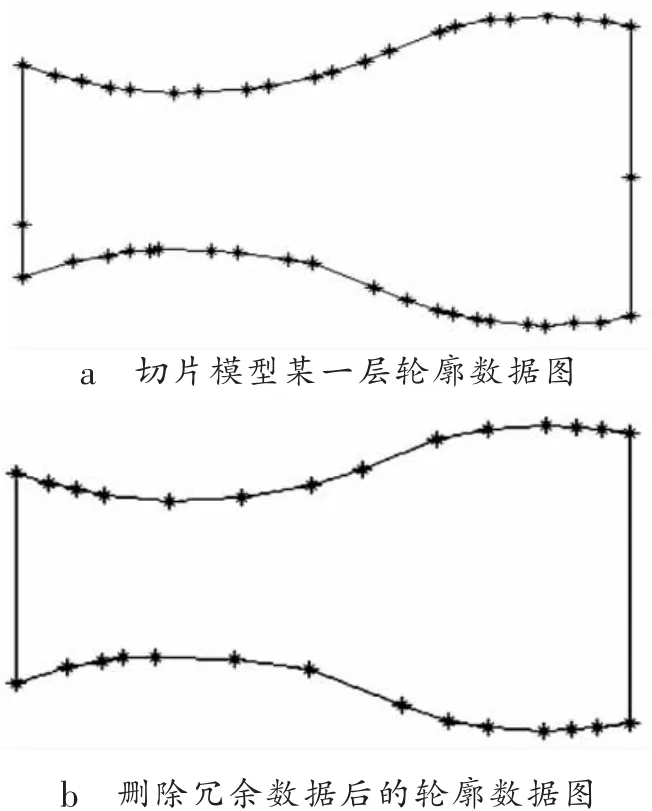
图4 轮廓数据的对比

2 NURBS刀路轨迹规划算法

基于CAD模型的直接切片算法的二维轮廓用NURBS曲线表示，这类算法虽然能提高加工精度，但需要特定软件支持，且运算量大、效率较低。基于STL模型的切片算法的二维轮廓用封闭多边形表示，将CAD模型转换为STL模型时，这类算法因给定的弦高差会导致加工精度下降，故将由STL模型切片得到的二维封闭轮廓分段拟合成NURBS曲线，再将其离散得到加工刀路轨迹就可以提高加工精度［2,9］。

2.1 轮廓的分段处理

在对经过预处理之后的轮廓数据点Pi( i =0,1,2,…,m)进行拟合之前，必须做进一步处理，才能判断二维轮廓中是否存在需要拟合的顶点。在本文中，我们采用角度与长度判断准则来判断待拟合的顶点，角度阈值设为 β ，并可根据模型成型精度自行定义。

任取3个连续的数据点 Pk−1、 Pk和Pk+1(k =1,2,…,m −1)，计算 Pk−1Pk与 PkPk+1之间的夹角 α （图3）。在判断长度时，先设定阈值 δ ，再根据弦高差的定义计 算 | Pk−1Pk|与 | PkPk+1|的长 度。

该方法可描述为：读取一个数据点，若该数据点不满足

或不满足

就以顺时针或逆时针的方式读取相邻的数据点，直到满足式（1）和式（2），并将该数据点作为拟合的起点 q0。依次读取数据点，若这些数据点满足式（1）和式（2），就将这些数据点作为轮廓的拟合点 qi( i = 1 ,2,… ,z )。若读到的数据点不满足式（1）或式（2），就将该数据点作为轮廓拟合的终点（记为qn），这样就可以得到待拟合的分段轮廓数据Ci={q0, q1,… ,qz, qn}(i= 1 ,2,…,t )（图5）。其中，数据点c与i对应的夹角不满足式（1），数据点 a、f、g、m 对应长度不满足式（2），因此可将二维轮廓分为4段进行NURBS拟合，这4段分别为abc、cdef、ghi、ijlm。

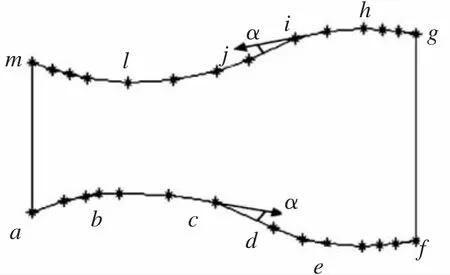
图5 轮廓的分段

2.2 三次NURBS拟合

2.2.1 NURBS曲线的定义

一条 k 次 NURBS 曲线［10］可表示为

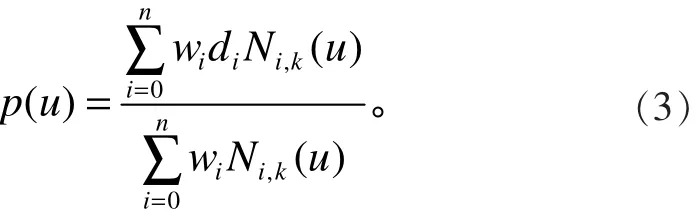
其中：wi( i = 0 ,1,2,… ,n)为权因子，采用NURBS拟合时，若权因子选择不当，会产生较大的非线性误差，因此取 wi= 1 ；di( i = 0 ,1,2,… , n)为控制顶点； Ni,k(u)为定义在节点矢量 U = ( u1, u2, uk, … ,un+k+1)上的第i个k次B样条基函数，其德布尔-考克斯递推公式为

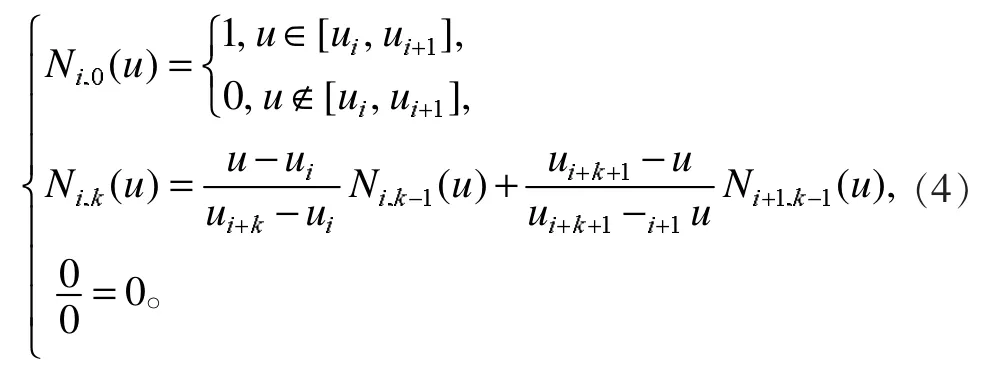
2.2.2 节点矢量的确定

由式（3）与式（4）可知，给定控制顶点 di和节点矢量U便可定义一条3次NURBS曲线。对于任意一条待拟合的分段轮廓，该轮廓存在 n +1个数据点。在反算控制顶点di的过程中，通常使首末数据点与曲线首末端点一致，并使内数据点变为曲线的分段连接点，以保证与三次NURBS曲线定义域的内节点对应［10］。该三次NURBS可由 n + 3 个控制顶点di( i = 0,1,2,… ,n, n +1,n+2)决定，对应的节点矢量为 U = ( u0, u1, …,un+5, un+6)。

节点矢量的确定可选择均匀参数法、向心参数法、积累弦长参数法等。在本文中，我们选择了积累弦长参数法，其中端节点的重复度为4，相应的积累弦长参数法公式［10］为

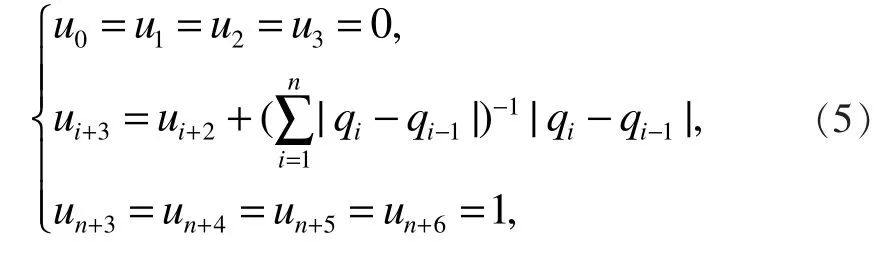
其中，i = 1,2,… ,n −1。

2.2.3 控制顶点的确定

将曲线定义域 u ∈ [ ui, ui+1]∈[0,1]内的节点值代入以下公式［11］

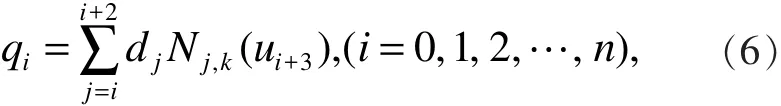
可得到 n + 1 个方程，但未知顶点个数为 n +3。由这n+1个方程无法解出 n +3个未知顶点数的对应的解。为了求解由这 n +1个方程组成的方程组，常常通过增加边界条件的方法增加附加方程，而边界条件的确定可通过选用自由端点、抛物线、切矢条件等实现。在本文中我们选取切矢条件公式

作为附加方程。

对于 C 2上的三次NURBS曲线，节点矢量的首、末节点的重复度为4，故有 d0= q0和 dn+2=qn，三次NURBS插值曲线的其他控制顶点可通过

经过节点矢量的确定与控制顶点的反求，通过式（3）便可确定一条NURBS曲线。图6为该二维轮廓的NURBS拟合效果。

图6 二维轮廓的NURBS拟合效果

2.3 刀路轨迹的确定

确定二维轮廓的分段三次NURBS差值曲线后，所有的刀触点都在该条曲线上。由于数控加工中输入的是刀触点的坐标，数控机床依据该坐标对毛坯进行加工，因此需要对NURBS曲线进行离散以获取刀触点。为了提高NURBS曲线在曲率变化较大处的离散精度，我们利用容差离散法对曲线进行离散。容差的定义见图7。其中：t为由加工精度定义的容差； Lstep为给出的步长，通常为0.05。刀触点的轨迹如图8所示。其中：图8a是步长等于0.05、容差等于0.06的刀触点轨迹图，图8b是步长等于0.05、容差等于0.04的刀触点轨迹图。

采用容差离散法获取刀触点步骤如下：

1）读取一条NURBS曲线。

2）U1为该NURBS的参数定义域的下界，取初值

3）计算 U1U2所对应的容差t。若t大于给定的容差，则有

4） U2大于该NURBS的参数定义域的上界，即U2>1，转向步骤1）；否则转向步骤3）。

5）所有NURBS曲线处理完，结束该程序。

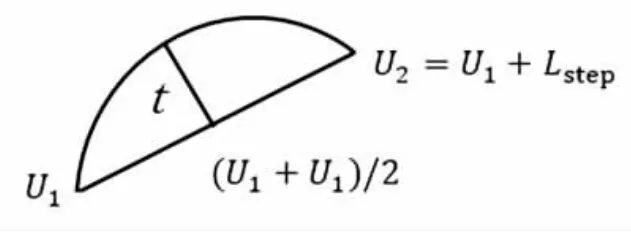
图7 容差的定义

图8 相同步长不同容差的刀触点轨迹

3 结论

在本文中，我们对STL模型切片形成的二维轮廓进行了分段三次NURBS插值，提高了STL模型切片的精度；利用容差离散法通过离散NURBS曲线获取了刀触点，提高了NURBS曲线在曲率变化较大处的离散精度，使得刀路轨迹变得更加精确，也使加工后的模型表面更加光滑。

参考文献：

［1］ ZHANG Z Y,JOSHI S.An improved slicing algorithm with efficient contour construction using STL files［J］.The international journal of advanced manufacturing technology,2015,80（5）:1347-1362.

［2］ 赵方.3D打印中基于STL文件的分层算法比较［D］.大连：大连理工大学，2016.

［3］ 赵萍，孙红.基于STL模型的数控加工路径规划［J］.机械设计与制造，2009（12）：169-170.

［4］ ZHU H,LI N.A new STL model-based approach for tool path generation in CNC incremental forming［J］.The international journal of advanced manufacturing technology,2013,69（1/2/3/4）:277-290.

［5］ 徐金亭，刘伟军，卞宏友，等.基于网格曲面模型的等残留刀位轨迹生成方法［J］.机械工程学报，2010， 46（11）：193-198.

［6］ LI M,ZHANG L C,MO J H,et al.Tool-path generation for sheet metal incremental forming based on STL model with defects［J］.International journal of advanced manufacture and technology,2012,63（5/6/7/8）:535-547.

［7］ 陈晓兵，廖文和.基于STL数据模型的NURBS刀轨生成算法［J］.组合机床与自动化加工技术，2010（11）：22-25.

［8］ 胡亮，黄志刚，梁远标.STL模型切片数据的生成算法研究［J］.机械工程与自动化，2016（2）：40-41.

［9］ 李成，杨继全，李超，等.基于NURBS曲线拟合的STL文件局部精度提高方法的研究［J］.南京师范大学学报（工程技术版），2013，13（1）：15-19.

［10］施法中.计算机辅助几何设计与非均匀有理B样条［M］.北京：高等教育出版社，2013：303-308.

［11］叶丽，谢明红.采用积累弦长法拟合3次NURBS曲线［J］.华侨大学学报（自然科学版），2010，31（4）：383-387.