基于博弈期权的BOT项目融资创新研究
王献东
(常州工学院数理与化工学院,江苏 常州 213032)
0 引言
BOT是英文Build-Operate-Transfer的缩写,通常直译为“建设—经营—转让”,也叫做“特许权融资模式”,是社会资本参与基础设施建设的一种有效的融资方式。由于BOT项目具有投资大、建设运营周期长、投资收益不确定因素多等特点,再加上各级政府和项目公司缺乏经验、决策不合理等原因导致项目提前终止的情况时有发生。国内外的学者对项目提前终止的原因和影响因素进行了分析并提出了一些针对提前终止的补偿方法。例如,Irwin和Mokdad[1]指出,提前终止补偿金额取决于提前终止的原因:如果提前终止是由私营部门的违约造成的,支付数额通常是项目的市场价值,该价值可以通过重新招标合同价格确定;如果是不可抗力(例如自然灾害),政府的支付通常与私营部门的债务相关,例如其股权的账面价值;如果提前终止是由政府的违约造成的,政府应充分赔偿债权人和股东的损失。Xiong 和 Zhang[2]介绍了两种基于财务报表和项目未来收益现金流量折现值的补偿方法。Song等[3]提出了一种采用ARIMA模型预测高速公路BOT项目未来的交通量、运行和维护成本以及未来的现金流,基于现金流来计算高速公路BOT项目提前终止补偿数量。
尽管世界上一些国家的特许经营协议已经开始引入提前终止的补偿条款,学者也提出了提前终止的补偿方法,但理论界和实务界就提前终止的影响因素和责任承担主体尚难以清晰地界定,致使条款的可操作性较差,项目提前终止的情况一旦发生,政府和项目公司很难就提前终止的补偿达成一致。因此,需要从另外的角度来对该问题进行研究。近年来,金融衍生工具期权被广泛地应用于项目融资特许权期决策和政府对基础设施项目的担保决策,如文献[4—7]。博弈期权,又称以色列期权,由Kifer[8]在2000年首先提出。该期权是一种在美式期权基础上给予发行方在期权有效期内任何时刻都可以进行赎回的新式期权,即在合约的有效期内,它的持有者(买方)可以在任意时刻执行合约,发行者(卖方)也可以在任意时刻终止合约。
本文运用金融工程思想创造性地解决了现有BOT项目协议中提前终止补偿条款可操作性差的问题,不仅可以为政府和项目公司提供决策参考,也对BOT等其他模式项目融资的创新具有一定的借鉴作用,因此,该方法具有一定的理论与实际意义。其创新点主要有两个方面:一是将博弈期权引入到项目融资协议中,提出一种创新的BOT项目融资;二是给出了博弈期权的定价方法。
1 基于博弈期权的BOT项目融资设定
1.1 博弈期权
博弈期权是在美式期权的基础上通过增加卖方终止合约的权利得到,因此它可以被看成是一种特殊类型的美式期权,该期权赋予了期权买卖双方在到期日T之前任何时刻t(0 下面给出博弈期权的数学定义。假设买方和卖方在0时刻签订一份到期日为T的博弈期权合约,该合约规定若买方先执行期权,则买方获得的权益是Xt;若卖方先终止合约,则卖方支付给买方的权益是Yt,并假定Xt (1) 假定政府与项目公司双方就某一个基础设施项目签订特许权协议,约定特许期为T。基于博弈期权买卖双方均可以在到期日之前提前执行或终止合约的特点,可以考虑将该期权引入到BOT项目协议中,用以解决现有的提前终止补偿条款可操作性差的问题。从更有利于保护项目公司权益的角度考虑,本文以政府作为博弈期权的卖方,项目公司作为博弈期权的买方,且根据BOT项目的特点可知该期权应为看跌期权。该期权合约规定:在特许期内的任意时刻t(0 设Mt表示项目公司在t时刻持有项目的价值,由博弈期权的定义可知:若项目公司在t时先执行期权将项目移交给政府,则项目公司获得的权益是max(Qt-Mt,0);若政府在t时提前回购项目终止协议,则项目公司获得的权益是max(Qt-Mt,0)+δ;若双方在T时之前都未执行期权,那么项目公司在特许期满T时将以回购价格K0将项目移交给政府;若双方决定在T时之前的同一时刻t终止合约,则项目公司获得的权益为max(Qt-Mt,0)。因此,如果项目公司提前将项目移交给政府的时间为τ,政府提前回购项目的时间为γ,则项目公司获得的权益R(τ,γ)可以表示为 (2) 期权的买方要获得期权所赋予的权利就需要支付一定的期权费用给期权的卖方,如何计算这一费用即博弈期权的价格,就成为政府和项目公司在签订期权合约时要考虑的一项重要内容。 计算博弈期权价格的首要工作是对标的资产价值的运动规律进行建模,根据BOT项目的特点,本文把项目公司持有的基础设施项目看作是博弈期权的标的资产。BOT项目中,项目公司在特许期内通过向用户收取费用或出售产品以回收投资、清偿贷款并赚取利润。由此可知,项目公司在t时刻持有项目的价值Mt就等于从t开始至特许期T(不包括t时刻)的T-t时间长度内,项目所获得的所有现金收益(项目收入减去运营成本)的折现。由于影响BOT项目收益的因素众多,因此,收益具有很大程度上的不确定性。为简便起见,本文采用Cox等[12]提出的基于离散时间的二叉树模型对每段时间内BOT项目的收益进行建模。 一般来说,BOT项目融资的特许期包含项目的建设与运营阶段,为了研究的方便,本文假设特许期就是运营阶段。将特许期T等分为n段,则每段时间的长度Δt=T/n。为简便起见,对任意的i=0,1,…,n-1,假定项目在时间段[iΔt,(i+1)Δt]上的现金收益只在时间区间的右端点时刻(i+1)Δt获得。根据市场调研和分析,可以预测项目正式运营后Δt时间长度内获得的初始现金收益为S,假设在Δt时间段内项目收益的上升因子为u,下降因子为d,在特许期的每个时间段[iΔt,(i+1)Δt]内收益上升的概率p和下降的概率p′均保持不变,且p+p′=1。在这里采用Cox等使用的条件u=1/d,使得许多节点重合,从而在很大程度上简化了树图。 图1给出了一个3阶段的项目收益二叉树图,设初始0时刻预测的项目收益为S,在Δt时项目收益要么上升到Su,要么下降到Sd;在2Δt时项目收益就有3种可能:Su2、Sud、Sd2;在3Δt时项目收益就有4种可能:Su3、Su2d、Sud2、Sd3。 图1 一个3阶段的项目收益二叉树 需要说明的是,本文构建的项目收益二叉树图与Cox等提出的股票价格二叉树图有一定的区别。Cox等股票价格二叉树图起点的“S”表示0时刻股票的价格是S,本文图1中起点的“S”并不表示0时刻项目获得的现金收益是S,而是表示项目正式运营后的Δt时间长度内现金收益的初始预测值为S,根据项目在每个时间段[iΔt,(i+1)Δt]上的现金收益只在时间区间的右端点时刻(i+1)Δt获得的假设,项目第一次获得现金收益的时间在Δt时刻,其收益为Su或Sd。 在构建了项目收益的二叉树模型之后,就可以在此基础上计算各节点上项目公司持有项目的价值。由于特许期满时项目公司需要将项目移交给政府,因此,在特许期T时各节点(n,j)上项目的价值Mn,j均为0。在特许期T之前,对任意的i=0,1,…,n-1;j=0,1,…,i,则在iΔt时节点(i,j)上项目的价值Mi,j就等于(i+1)Δt时的节点(i+1,j)与(i+1,j+1)上项目价值的数学期望在Δt时间长度内的折现,再加上节点(i+1,j)与(i+1,j+1)上项目获得现金收益的数学期望在Δt时间长度内的折现。例如,将BOT项目的特许期等分为3段,则对于项目公司来说,节点(3,j)上项目的价值 M3,j=0j=0,1,2,3 (3) 在2Δt时节点(2,0)上项目的价值M2,0就等于节点(3,0)和(3,1)上项目现金收益的加权平均在时间长度Δt内的折现,即 (4) 类似地,节点(1,1)上项目的价值就等于节点(2,1)和(2,2)上项目价值的加权平均在时间长度Δt内的折现,再加上节点(2,1)和(2,2)上项目现金收益的加权平均在时间长度Δt内的折现,即 (5) 一般地,若将项目的特许期等分为n段,则在iΔt时节点(i,j)上项目公司持有项目的价值Mi,j可以表示为如下的递推公式: (6) 利用式(6)递推就可以求出在任意节点上项目的价值。 博弈期权是在美式期权的基础上增加了期权卖方在到期日之前任意时刻可以终止合约的权利,使得该期权比美式期权更加复杂。由期权定价理论可知,期权的价格等于期权买方未来获得权益的折现在风险中性测度下的数学期望。因此,由博弈期权的定义可知,如果项目公司将项目移交给政府的时间为τ,政府提前收回项目的时间为γ,则博弈期权的公平价格V0应该为 (7) 其中:E(·)表示在风险中性测度下的数学期望;τ∧γ=min(τ,γ),表示τ和γ两者中较小的一个。 本文采用二叉树期权定价方法来研究BOT项目融资中博弈期权的定价,其计算步骤如下: 步骤1:计算特许期满时各节点上的期权价值。 在特许期T时,各节点(n,j)上项目公司持有项目的价值Mn,j均为0,项目公司可以回购价格K0将项目移交给政府。因此,在T时各节点(n,j)上期权的价值Vn,j均为K0,即 Vn,j=K0j=0,1,…,n (8) 步骤2:计算特许期满之前各节点上的期权价值。 在计算出特许期T时各节点上的期权价值之后,就可以用倒推的方法来计算特许期T之前各节点上的期权价值。 首先,计算T的前一个时刻,即(n-1)Δt时各节点上的期权价值。在(n-1)Δt时节点(n-1,j)上期权的执行情况有四种:项目公司提前移交项目、政府提前回购项目、双方同时执行期权和双方均不执行期权。因合约规定若双方决定在同一时刻执行期权,则卖方支付给买方较小的权益,因此可以把双方同时执行期权看成是买方先执行期权。综上所述,节点(n-1,j)上期权的价值Vn-1,j可以表示成 Vn-1,j=min(gn-1,j,max(fn-1,j,hn-1,j))j=0,1,…,n-1 (9) 其中: fn-1,j=max(Q(n-1)Δt-Mn-1,j,0)j=0,1,…,n-1 (10) 表示在(n-1)Δt时项目公司移交项目,节点(n-1,j)上项目公司得到的权益;gn-1,j=fn-1,j+δ表示政府在(n-1)Δt时提前回购项目,节点(n-1,j)上项目公司得到的权益; (11) 表示在(n-1)Δt时项目公司不移交项目,继续持有到下一时刻nΔt(即特许期满时),项目公司获得权益的数学期望在Δt时间内的折现。 其次,由(n-1)Δt时刻各节点的期权价值计算(n-2)Δt时各节点上的期权价值,再按照从后往前倒推,依次计算(n-3)Δt,…,Δt时各节点上的期权价值。例如,在iΔt时节点(i,j)上博弈期权的价值Vi,j可以表示成 Vi,j=min(gi,j,max(fi,j,hi,j))i=n-2,n-3,…,1;j=0,1,…,i (12) 其中: fi,j=max(QiΔt-Mi,j,0) (13) 表示项目公司在iΔt时移交项目,节点(i,j)上项目公司得到的权益;gi,j=fi,j+δ表示政府在iΔt时提前回购项目,节点(i,j)上项目公司得到的权益; (14) 表示在iΔt时,项目公司不移交项目,继续持有项目公司获得权益的数学期望在Δt时间内的折现。 步骤3:计算博弈期权的价格。 根据Δt时刻两个节点(1,0)和(1,1)上的期权价值V1,0和V1,1,可以计算0时刻博弈期权的价格为 (15) 以上给出的BOT项目融资中博弈期权的二叉树定价方法比较简单、易懂,在实际计算时可以运用Matlab软件编程实现上述算法。 在这一部分给出一个引入博弈期权的BOT项目融资的算例分析,并对影响博弈期权价格的参数:初始收益、回购价格、特许期、补偿金、上升因子和利率进行敏感性分析。假设政府与项目公司就某一项基础设施签订BOT特许权协议,规定特许期T=20年。 最后,按照2.3节给出的博弈期权二叉树定价算法可以计算出博弈期权的价格为1.585 2×103万元。 由本文构建的模型可知,影响BOT项目中博弈期权价格的因素有6个:初始收益、回购价格、特许期、补偿金、上升因子和利率。为了研究博弈期权价格对各参数的敏感性,以上述参数的取值:S=2,K0=1,T=20,δ=1,u=1.1和r=0.05为基准,图2—7分别给出了初始收益、回购价格、特许期、补偿金、上升因子和利率6个参数中的1个参数在某一范围内变化而其余5个参数保持不变时博弈期权价格的变化趋势。 由图2至图7可以看出,博弈期权的价格随着初始收益、回购价格、特许期、补偿金和上升因子的增加而增加,随着利率的增加而减小。经过多次改变参数的取值计算后发现,以上博弈期权的价格与6个参数之间的变化规律仍然成立。因此,本文所建立的模型具有较好的可靠性,可以为政府和项目公司在签订合约时提供决策参考。 图2 不同初始收益下博弈期权的价格 图3 不同回购价格下博弈期权的价格 图4 不同特许期下博弈期权的价格 图5 不同补偿金下博弈期权的价格 图6 不同上升因子下博弈期权的价格 图7 不同利率下博弈期权的价格 本文采用二叉树模型对每段时间内项目的收益进行建模,基于构建的模型计算项目公司持有项目的价值,并给出BOT项目融资中博弈期权的二叉树定价算法,最后的算例分析证明了方法的可行性,可以为政府和项目公司提供决策参考。引入博弈期权的BOT项目融资,允许政府和项目公司根据项目的实际运营状况、社会经济发展的需要来动态地调整决策,一定程度上解决了现有的提前终止补偿条款可操作性差的问题,增加了项目合约执行的灵活性,提高了项目的吸引力,为项目融资的改进提供了一种全新的视角,具有一定的理论与实际意义。二叉树模型的优点是比较简单、直观,其缺点是不能很好地刻画不确定性环境中项目收益的随机变化规律,因此,今后需要进一步研究如何改进模型。 [参考文献] [1]IRWIN T, MOKDAD T. Managing contingent liabilities in public-private partnerships: Practice in Australia, Chile, and South Africa[R/OL]. [2017-09-08].http://www.docin.com/p-423242862.html. [2]XIONG W, ZHANG X. Compensation approaches for early termination of PPP projects[C]. Proceedings of the 17th International Symposium on Advancement of Construction Management and Real Estate, 2014,721-729. [3]SONG J, FU Y, BAGAYA O. Compensation mechanism for early termination of highway BOT projects based on ARIMA model[J]. International Journal of Architecture, Engineering and Construction, 2016,5(1):53-60. [4]赵国杰, 何涛. 基于实物期权的BOT项目特许期决策模型研究[J]. 北京理工大学学报(社会科学版), 2010,12(5):27-30. [5]LV J N, YE G, LIU W, et al. Alternative model for determining the optimal concession period in managing BOT transportation projects [J]. Journal of Management in Engineering, 2015,31(4):1-7. [6]高峰, 郭菊娥, 赵强兵. 基于障碍期权的基础设施项目政府担保价值研究[J]. 预测, 2007,26(2):76-80. [7]牛静, 扈文秀, 穆庆榜, 等. 基于实物期权的基础设施投资担保负担测度及其风险管理研究[J]. 管理评论, 2012,24(8):11-20. [8]KIFER Y. Game options [J]. Finance and Stochastics, 2000,4(4):443-463. [9]宋斌, 林则夫, 刘黎黎, 等. 基于博弈期权的可转债定价模型及其实证研究[J]. 系统管理学报, 2013,22(6):758-767. [10]LEUNG C M, CHEN N, KWOK Y K. Game options analysis of the information role of call policies in convertible bonds [J]. Applied Mathematical Finance, 2015,22(4):297-335. [11]KO C C, LIN T T, YANG C. The venture capital entry model on game options with jump-diffusion process[J]. International Journal of Production Economics, 2011,134(1):87-94. [12]COX J C, ROSS S A, RUBINSTEIN M. Option pricing: A simplified approach[J]. Journal of Financial Economics, 1979,7(3):229-263.1.2 基于博弈期权的BOT项目融资公式
2 BOT项目融资博弈期权的定价过程
2.1 项目收益模型的构建
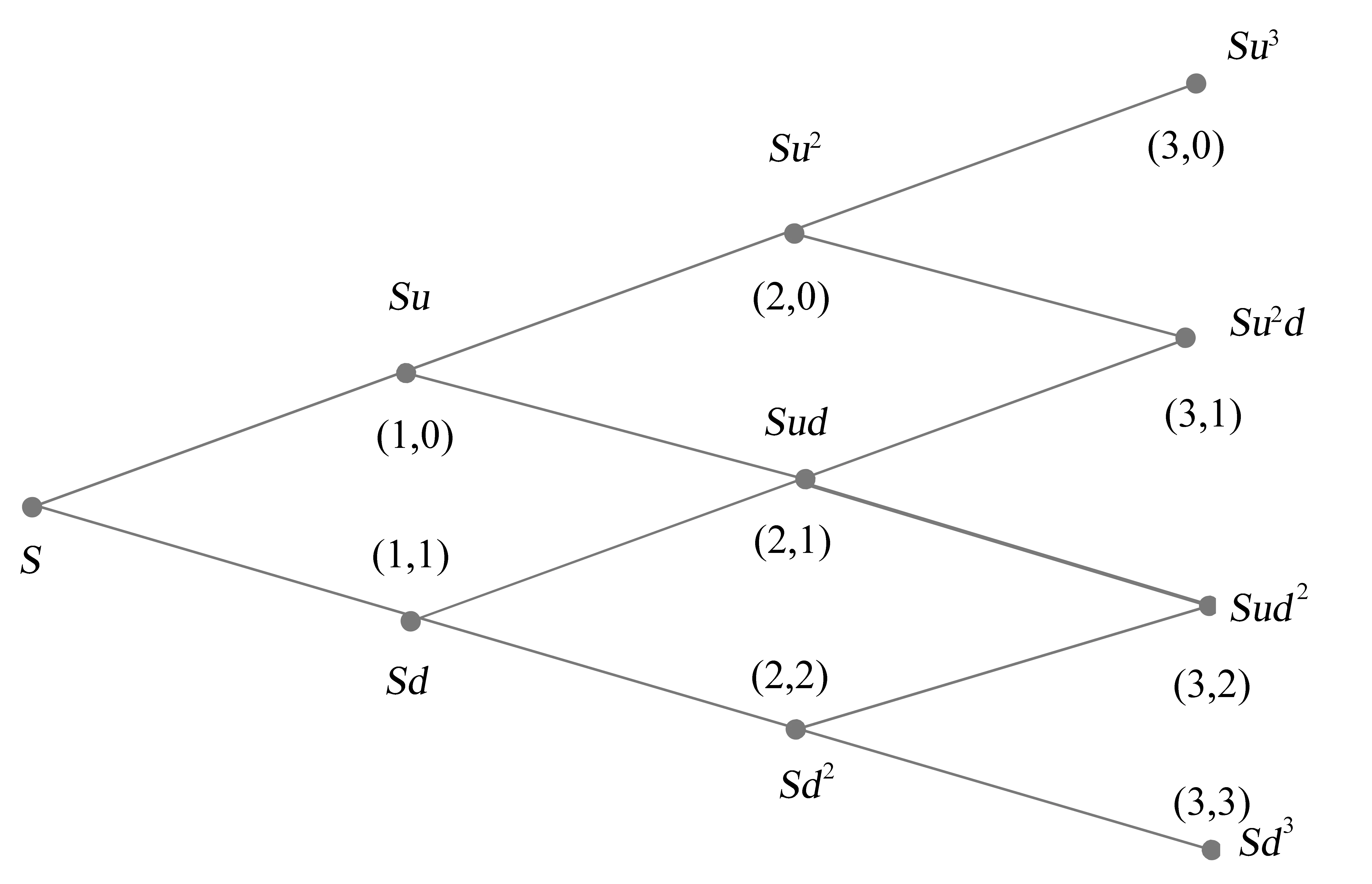
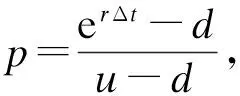
2.2 项目价值的计算
2.3 BOT项目融资中博弈期权的定价
3 算例分析
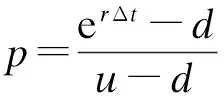
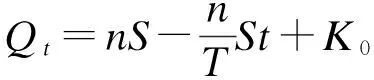
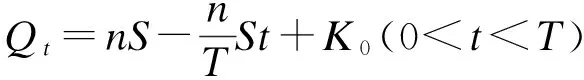
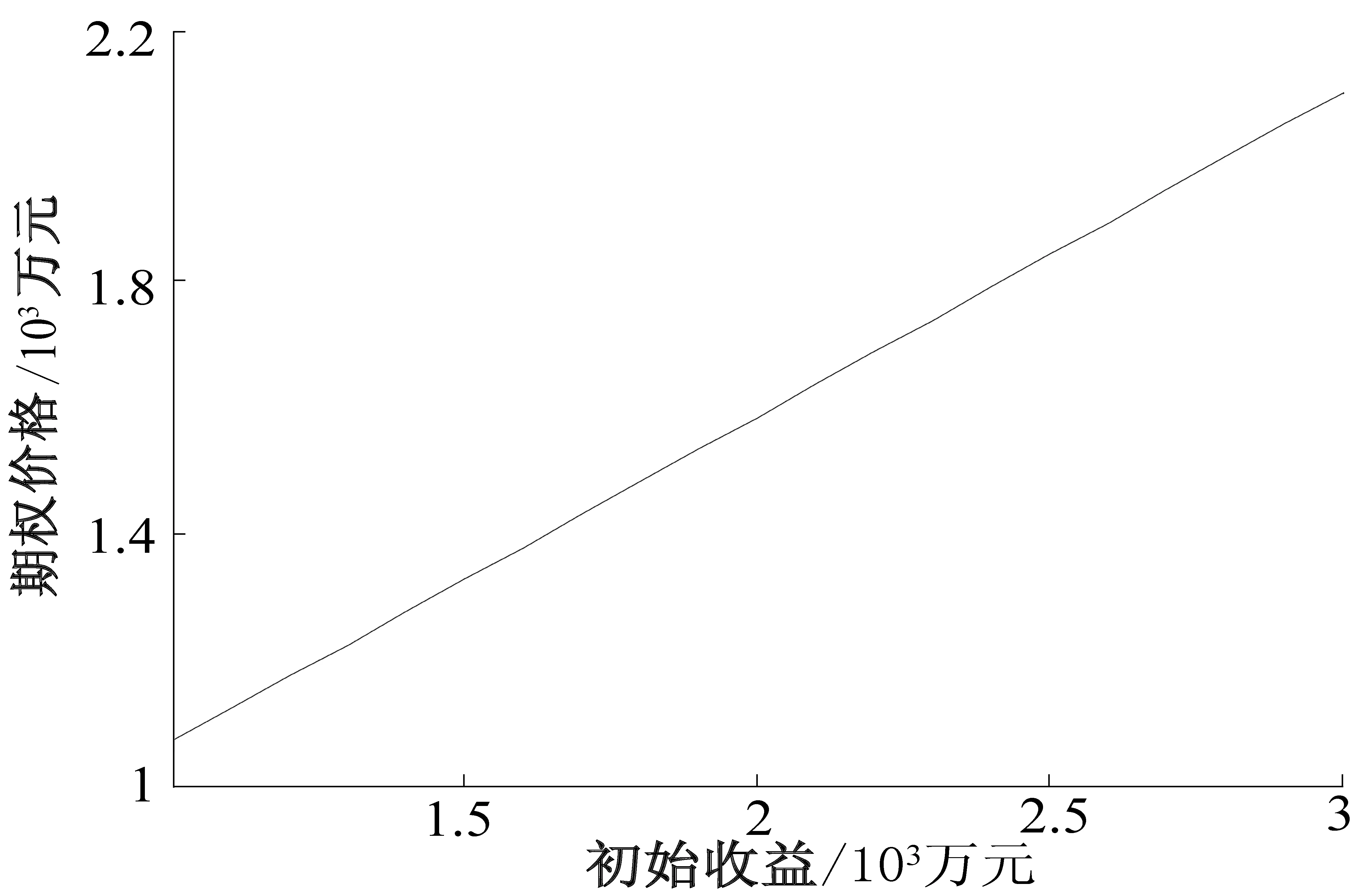
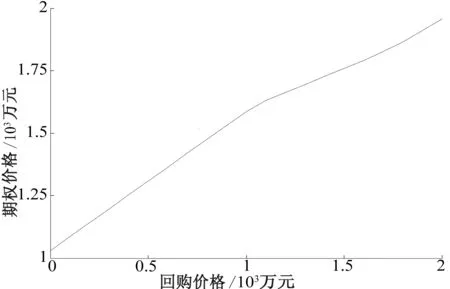
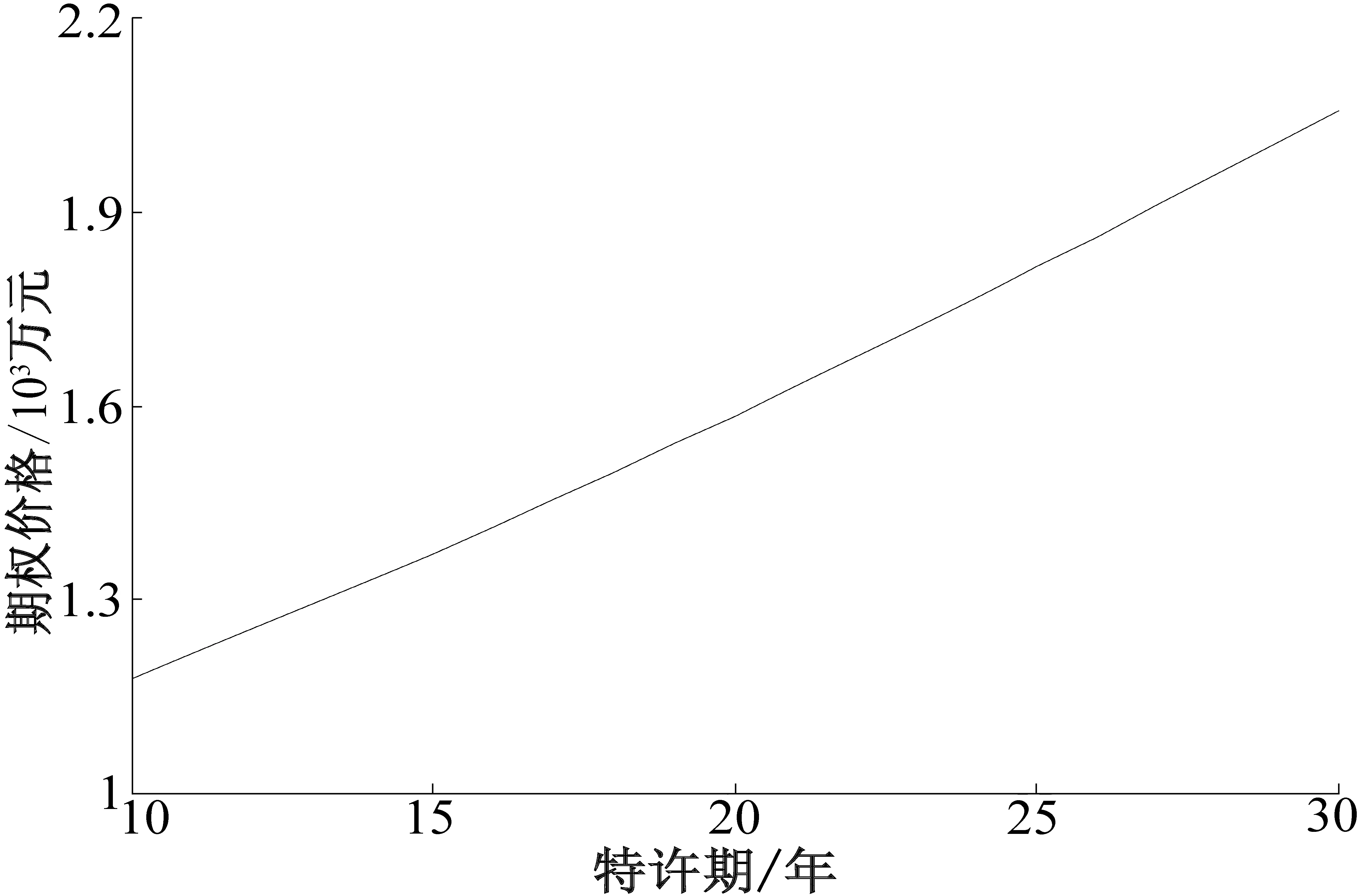
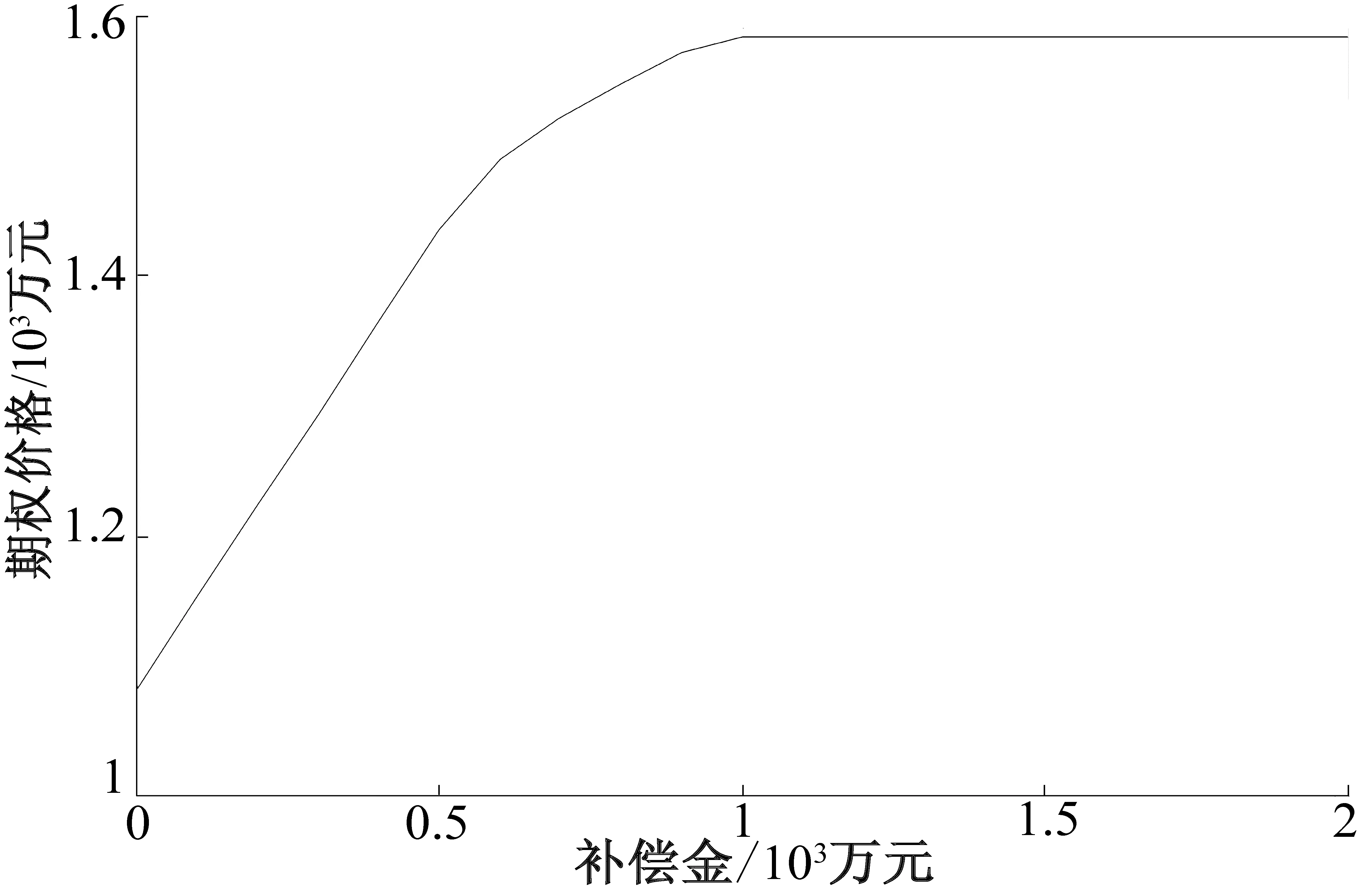
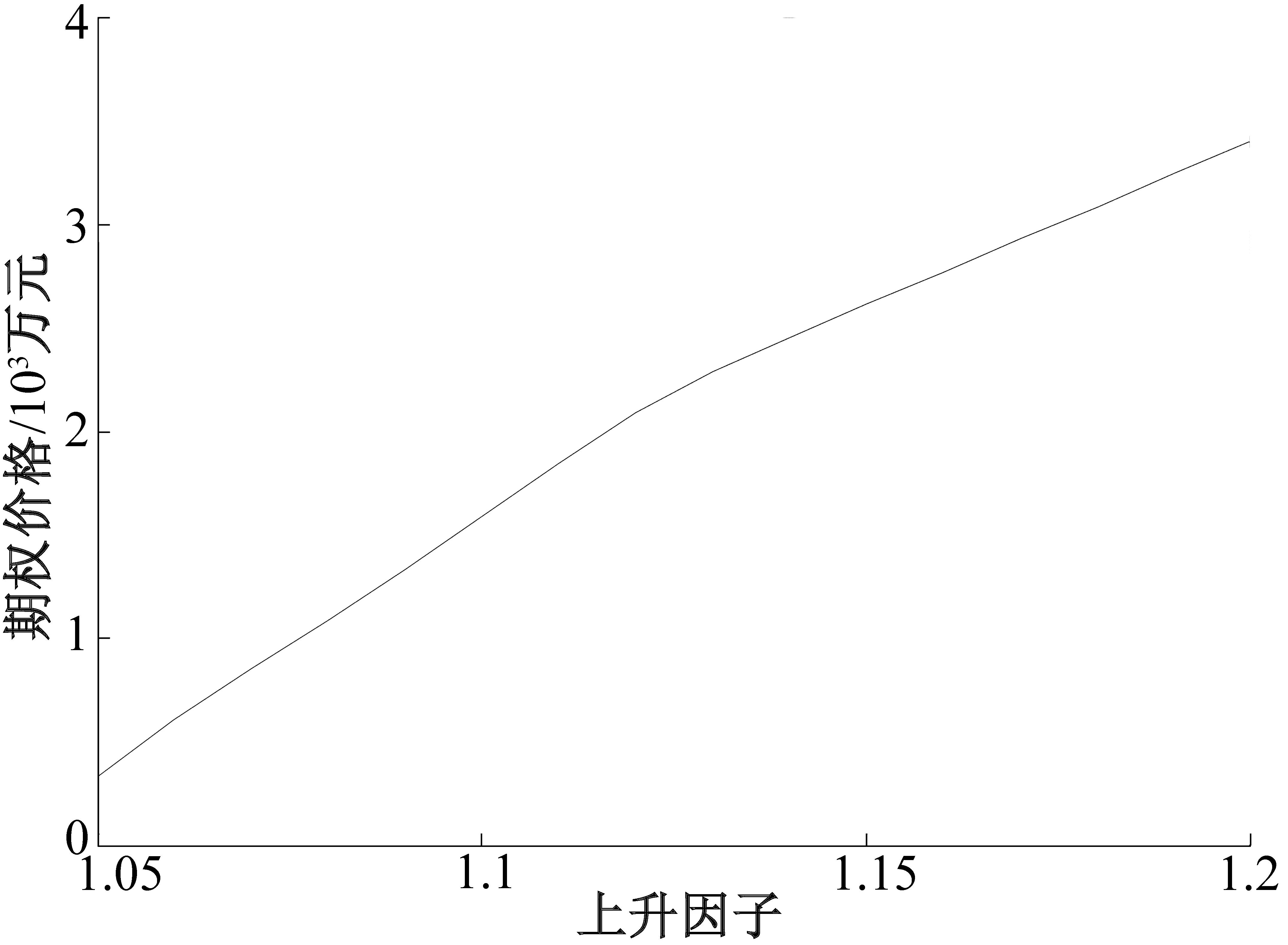
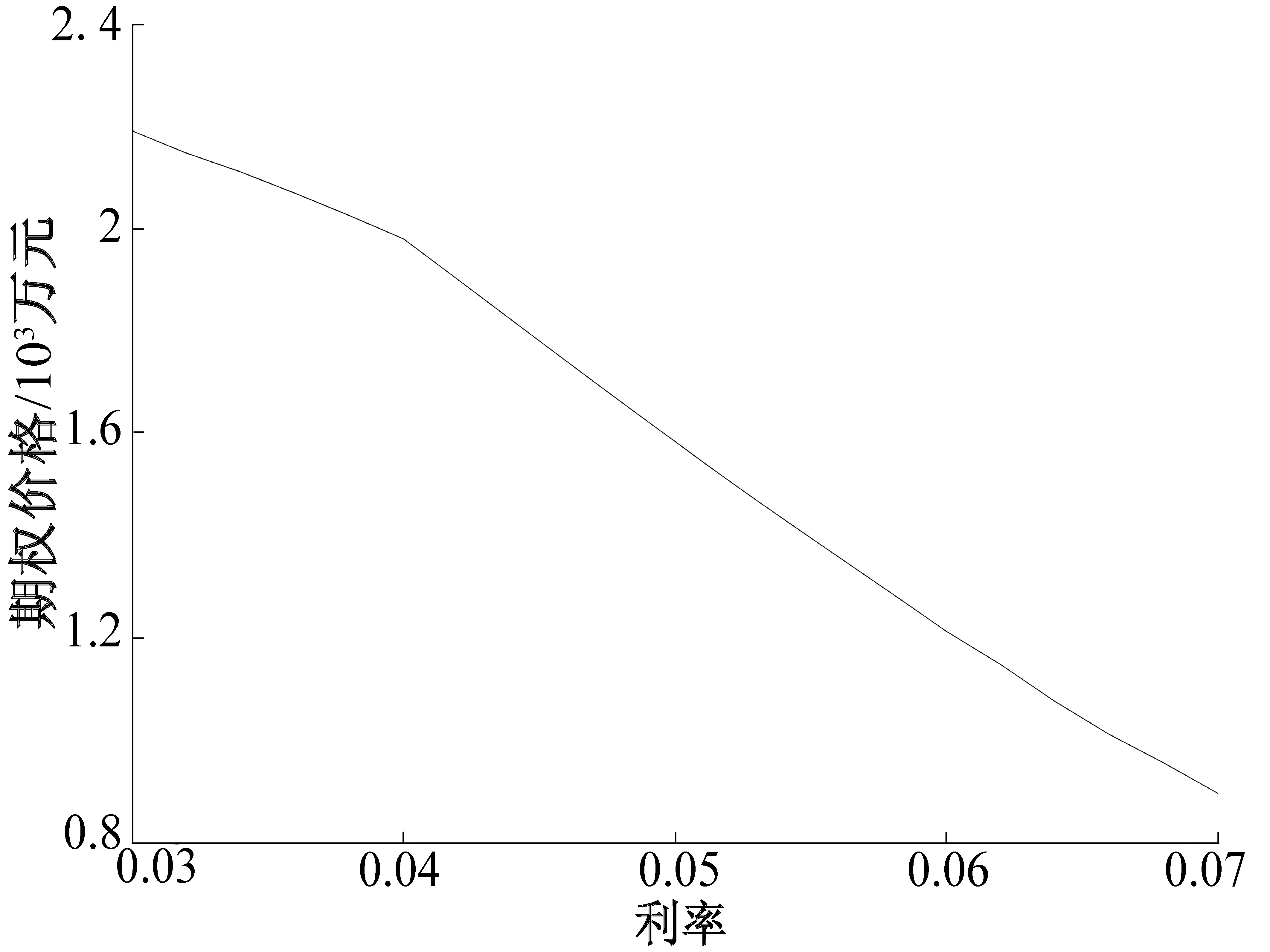
4 结论

