带裂缝梁的裂纹拓展分析

刘昊，常军，杨文凯

(1.苏州科技大学土木工程学院，江苏 苏州 215011；2.苏州市建筑工程设计院有限公司，江苏 苏州 215129)

断裂力学是最近几十年才发展起来的一门新兴学科，主要研究带裂纹或缺陷的物体在外力或外部环境作用下，其内部裂纹的扩展规律或其内部缺陷的失稳开裂等问题[1]。在断裂力学还未成型的年代，人们用传统的材料力学中的强度计算方法验证构件安全可靠性，然而在具体应用中发现，有些构件虽然满足了理论上的强度计算条件，但是它仍会在低应力情况下发生断裂破坏事故。按照传统的强度理论观点来处理这些构件，如使用强度更高的材料、加大构件的尺寸等，并不能有效解决构件低应力情况下的断裂问题[2-3]。随着对许多相似的低应力断裂问题的分析和研究，终于发现了导致这些问题的源头——裂纹扩展[4]。这一发现使人们找到了新的研究方向，也是断裂力学形成的直接原因。

研究裂纹拓展对提升工程整体的安全性有重大意义。本文主要研究了含预置裂纹的铝合金梁在三点弯作用下裂纹的发生与扩展，采用有限元模拟(利用Abaqus软件分析)和具体实验结合分析的方法，来研究铝合金梁在三点弯作用下当其中间自带一个损伤部位时，该部位裂纹的扩展情况和裂纹周边的应力应变情况，以及当裂纹开始发生扩展时梁上的受力分析。

1 带裂纹梁的设计

1.1 梁的材料及力学性能

实验采用T6061铝合金，该铝合金通过热处理预拉伸工艺生产[5]，虽然其强度与其他几种铝合金相比较差，但是韧性较好，便于加工，有利于实验时预加裂缝的操作，而且该型号铝合金致密没有杂质，内部缺陷少，因此其用途非常广泛[6]。在进行有限元模拟分析时，定义的构件也都是无缺陷的，用该种铝合金能更加贴合之后的有限元分析[7]。

铝合金的化学成分如表1所示，力学性能如表2所示。

表1 试验用铝合金化学成分 %

表2 试验用铝合金力学性能

为使有限元模拟更加精确，通过拉伸实验测量该铝合金的属性，得到其材料属性为：弹性模量68.9 GPa，泊松比0.33，密度2.7 g/cm3=2 700 kg/m3，屈服应力276 MPa，最大主应力为84.4 MPa，损伤稳定黏性为0.001。

1.2 梁的尺寸及预置裂纹位置处理

实验中铝合金构件截面尺寸为30 mm×10 mm，长度为110 mm。在构件下部中点处，预置一个10 mm×1 mm的U型凹槽作为裂缝，如图1所示。

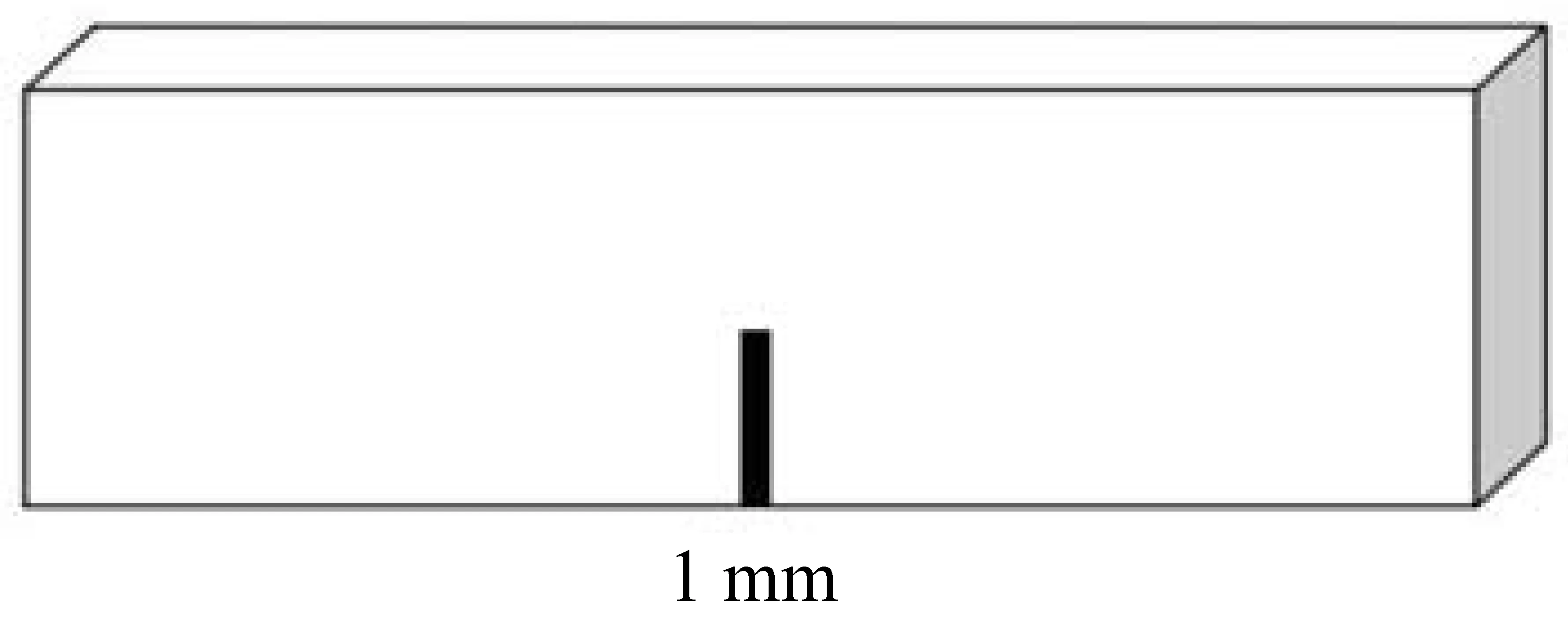
图1 带缺陷构件示意图

2 裂纹拓展有限元分析

2.1 拓展有限元法XFEM

本文采用的裂纹模拟技术是拓展有限元法XFEM，1999年Belytschko等[8]首先提出了扩展有限元法的概念。扩展有限元法是在传统有限元法基础上的发展，该方法使用整体划分有限元部件的理论，该理论1996年由Melenk等[9]提出,在该理论的指导下，可以在有限元分析中合理地插入裂纹的扩展函数(spread function),该函数通过分析有限元单元的自由度来推导出裂纹扩展时的间断性特点[10-12]。

扩展有限元法利用单位分解思想，通过在近似位移表达式中增加能够反映裂纹面的不连续函数及反映裂尖局部特性的裂尖渐进位移场函数，间接体现裂纹面的存在，同时反映了不连续面的局部特性，克服常规有限元进行断裂分析时的缺点，可以使裂纹穿过单元内部，不需预设开裂路径，裂纹扩展以后不需要重新划分单元网格，采用同一网格就可以分析任意位置裂缝问题[13]。

2.2 有限元模拟分析

建立一个横截面为30 mm×10 mm，长度为110 mm的模型，并在下部中点处，预置一个10 mm×1 mm的U型凹槽。由于是三点弯实验，为了最终效果与实验更加相近，需要再创建2个部件来模拟实验时的支座和加载的夹具部分，再将这三者装配起来，相互之间使用绑定约束连接。最终的装配结果如图2。

图2 有限元装配结果示意图

由于研究的是带裂纹铝合金构件的裂纹拓展情况，因此需要为该材料添加损伤演化属性，损伤演化即是该铝合金材料发生破坏时其内部细观结构所遵循的破坏规律，而所用的T6061铝合金最大主应力为84.4 MPa，损伤稳定黏性为0.001。对于另外的支座和夹具部件，采取刚体约束。

使用XFEM模块来分析裂纹拓展，对于部件的网格划分就不用再像其他的分析模块那样需要对裂纹尖端进行加密处理，只需要正常划分统一的网格。在本次Abaqus分析中使用3CD8R六面体网格划分技术。在三维网格划分中，要达到相同的精度，六面体使用的网格比四面体更少，分析构件的变形特性更完善，计算精度也更高[14]。由于实验室的试验机采用的是按位移加载，因此在有限元分析时也应该使用位移加载模块。XFEM裂纹技术能够在加载过程中，自动分析出部件的薄弱部分，自动产生并发展裂纹。

当有限元作业完成后，首先观察构件底部的情况，如图3、图4所示，在U型凹槽的正中间那块单元上率先出现了裂纹，随着继续加载，这条裂纹将会发展至整个凹槽的上表面。这就是裂纹初始形成的阶段。

图3 底部未开裂

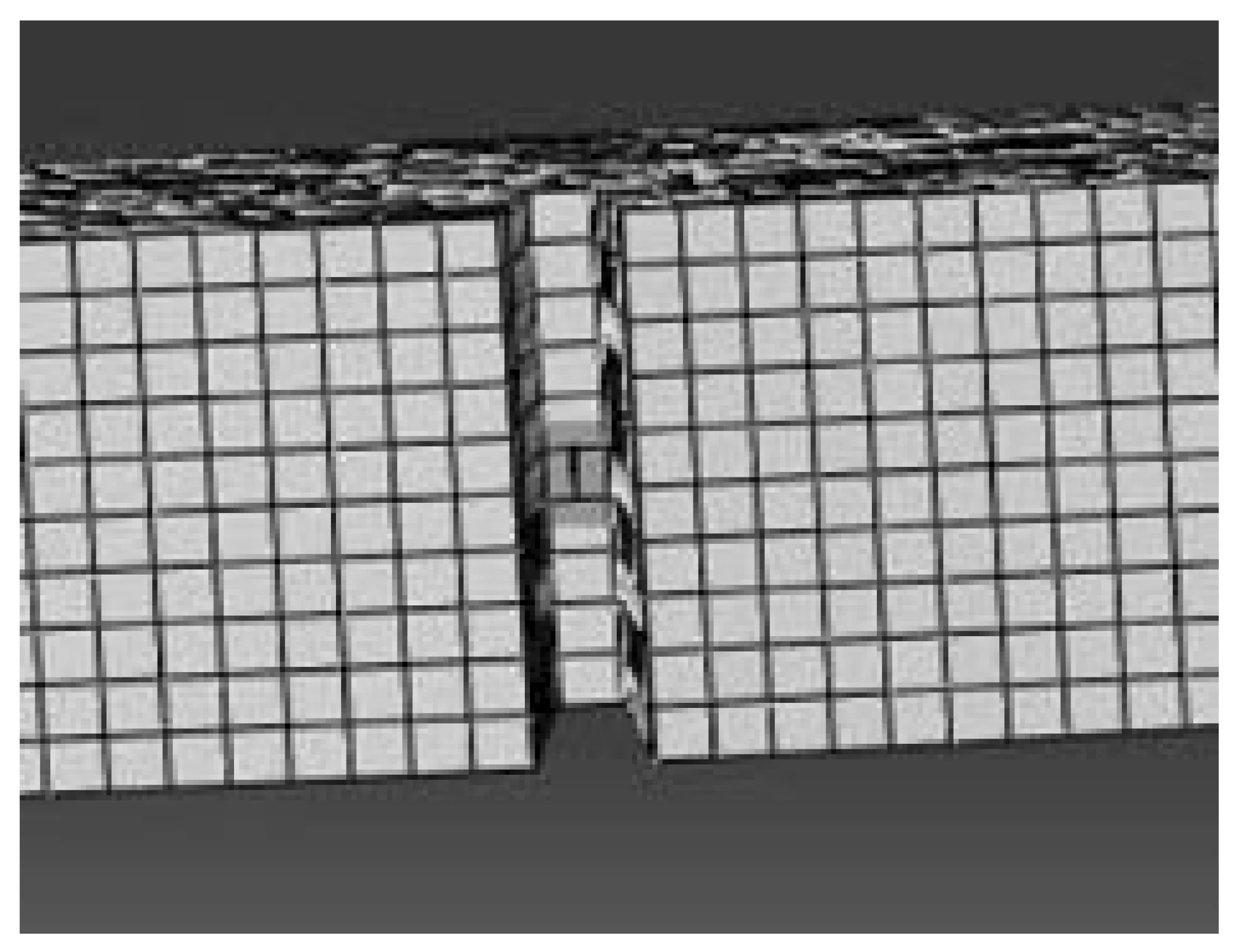
图4 底部发生开裂

随着裂纹的发展，裂纹将在正表面出现，然后继续向上发展，直至构件最终破坏，图5、图6就是有限元模拟的裂纹发展的整个过程。

图5 正表面裂纹开始形成

图6 正表面裂纹发展

以上是分析裂纹的产生与生长，接下来是分析单元的损坏。观察到裂纹生长过程中，裂纹周围单元的损坏，如图7、图8所示。首先，在凹槽顶部率先发生裂纹的那一排单元将率先出现损坏失效，然后在U型凹槽的两个直角处发生了单元的损坏失效，再以这两个直角处的损害为起点，以裂纹向上开裂为主方向，构件的单元将逐渐失效，直至最后的破坏。

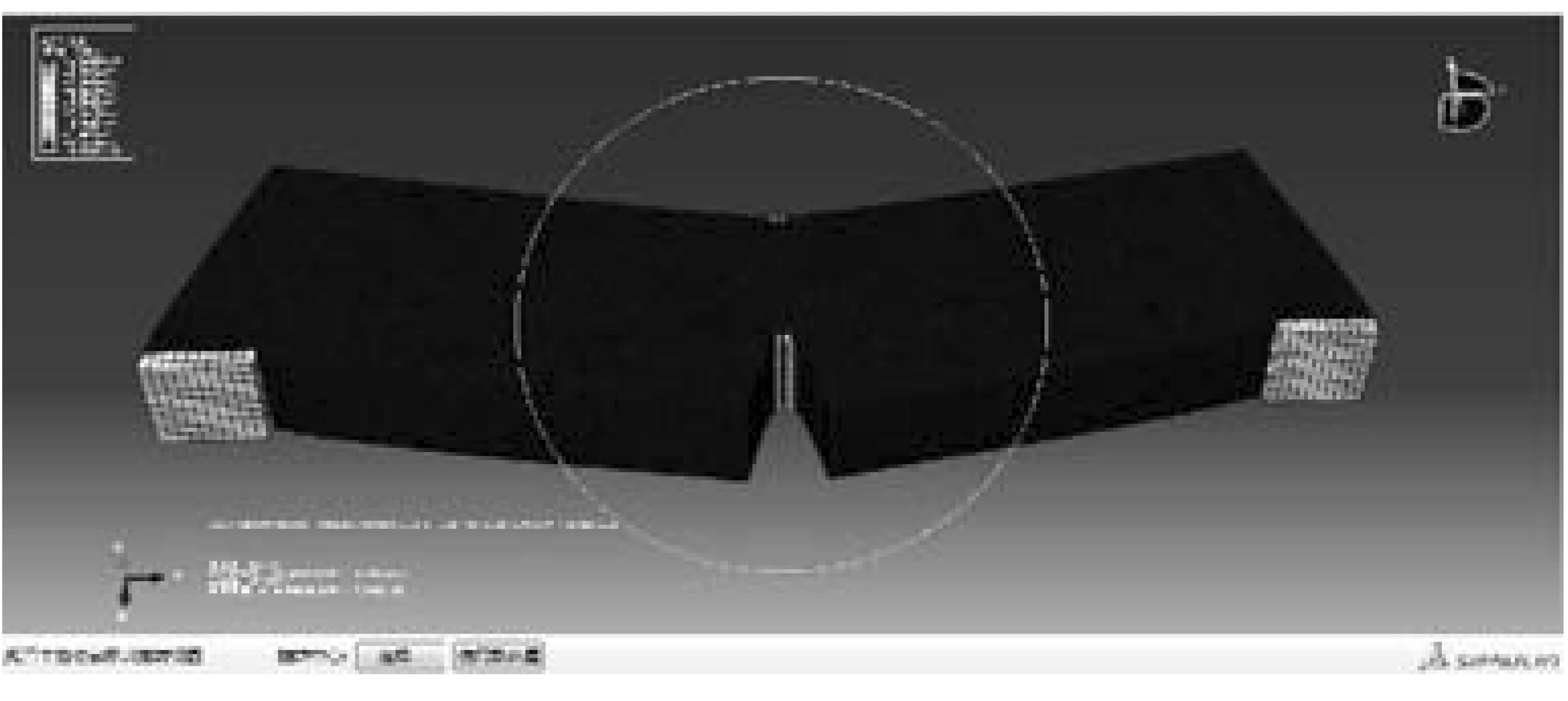
图7 凹槽顶部单元失效

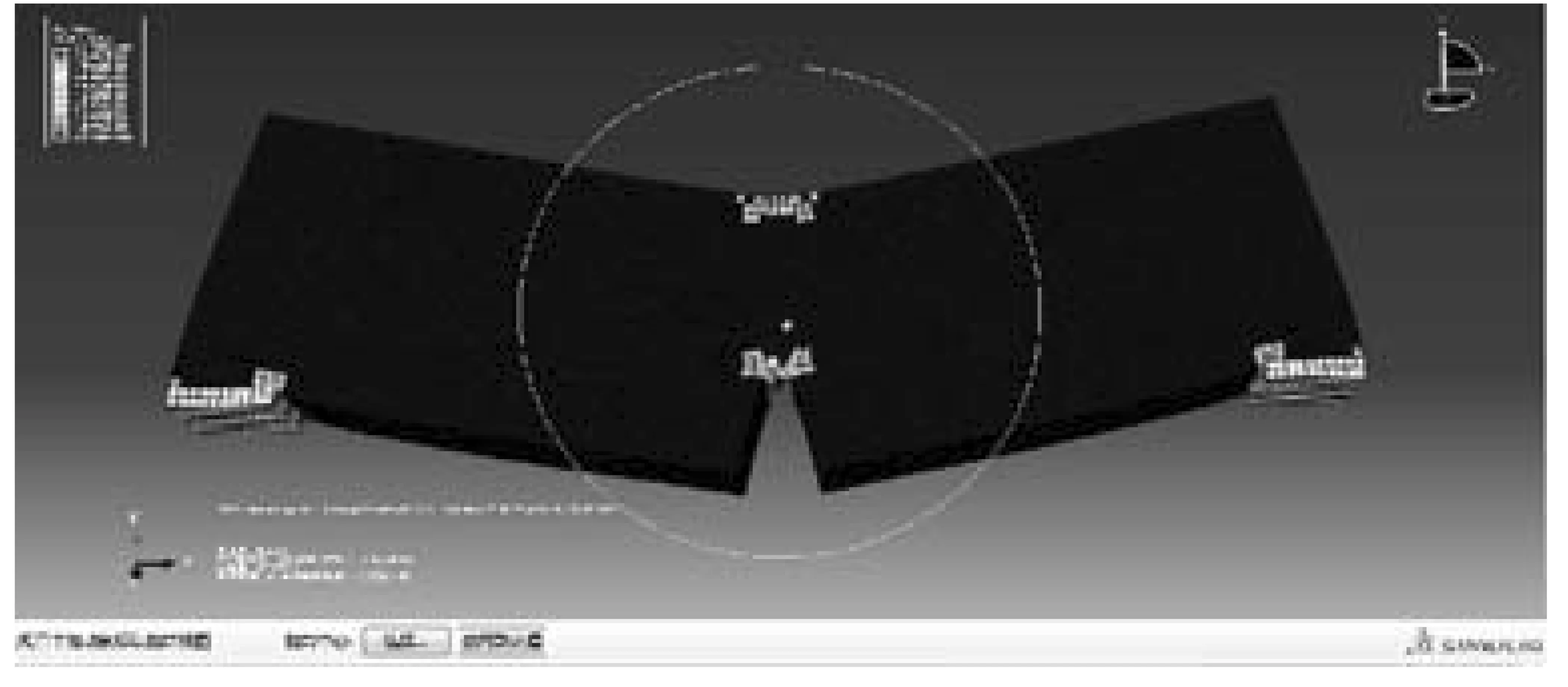
图8 凹槽两个直角处损坏

3 三点弯实验及分析

本次铝合金三点弯裂纹拓展实验中使用到的实验仪器有：20 kN电子万能试验机，2台高速相机，计算机，标定板，光源。如图9所示。

图9 实验仪器

在进行实验之前，通过电子万能试验机自带的电脑功能来定义加载的过程，实验过程中夹具上的力按位移加载[15]。

将构件放到支座上进行三点弯实验，在实验过程中可以观察到铝合金梁的裂纹的产生与拓展(图10、图11)，2台高速相机将完整地记录下整个过程，用做后期分析。

图10 裂纹开始形成 图11 裂纹完全形成， 构件被破坏

3.1 实验结果与Abaqus结果的对比分析

图12、图13分别为试验加载图和有限元加载图，把实验中的结果与有限元分析的结果进行对比分析。

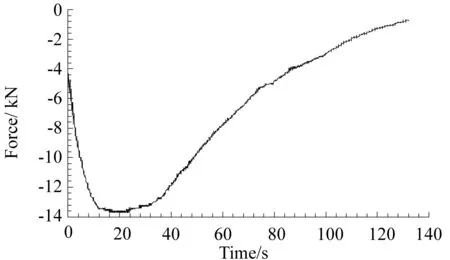
图12 试验加载图

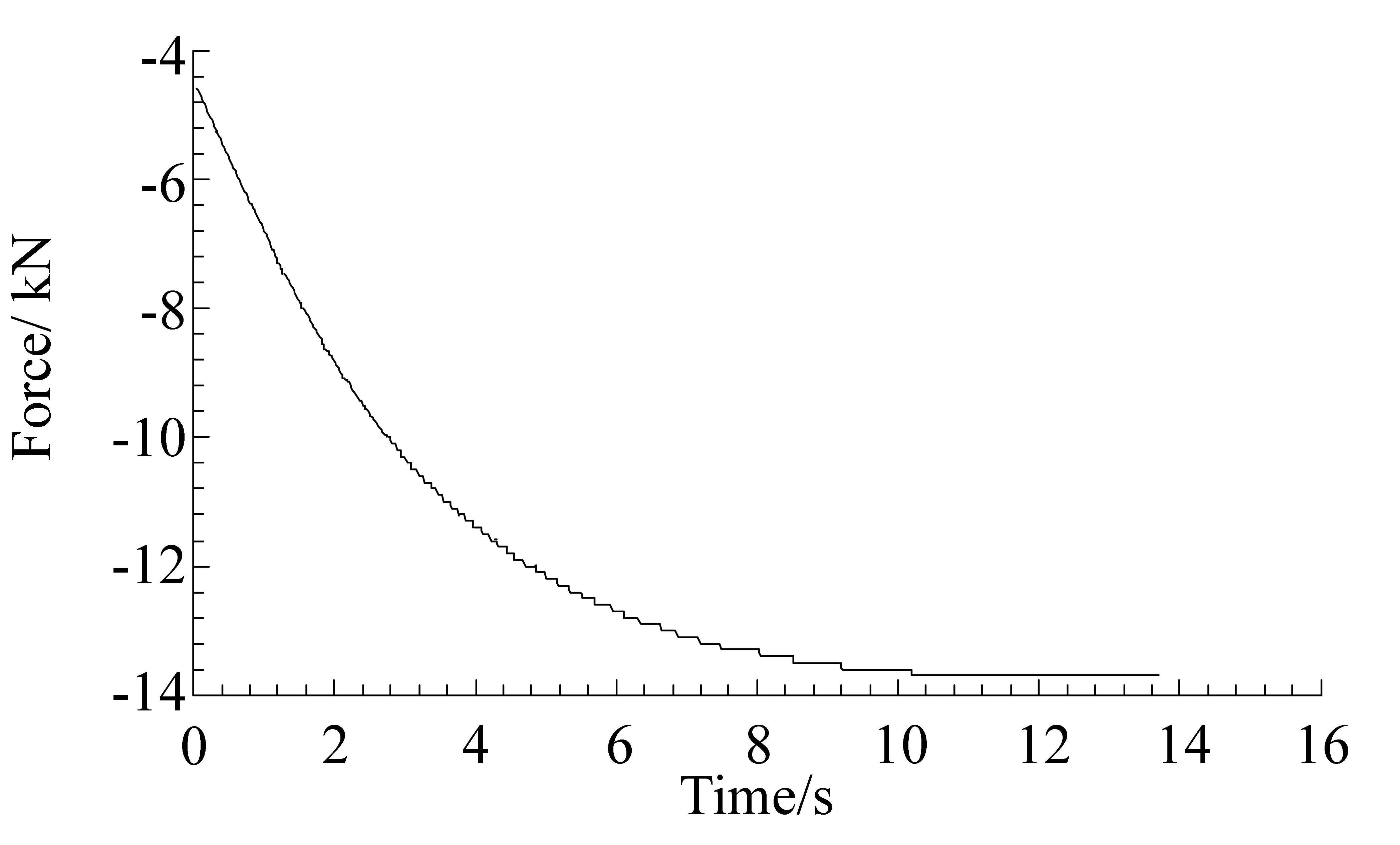
图13 有限元加载图

如图所示，试验加载至铝合金梁完全损坏时的载荷为13 749 N，而有限元分析时加载至梁损坏所用载荷为13 866 N。误差仅0.85%，说明在加载上有限元模拟与实验基本贴合，为之后的分析奠定了基础。

观察实验和有限元模拟时，由图14、图15可见，刚开始形成裂纹时的应变云图看上去有些不同，但考虑到实验时拍摄的区域由视场而定，而且应变过低的部分不能完全表达出来，因此只分析应变集中的部分，也就是预置U型凹槽的两个直角处。图中可以看出在两个直角处的应变分布最大，这进一步验证了有限元模拟实验的准确性。

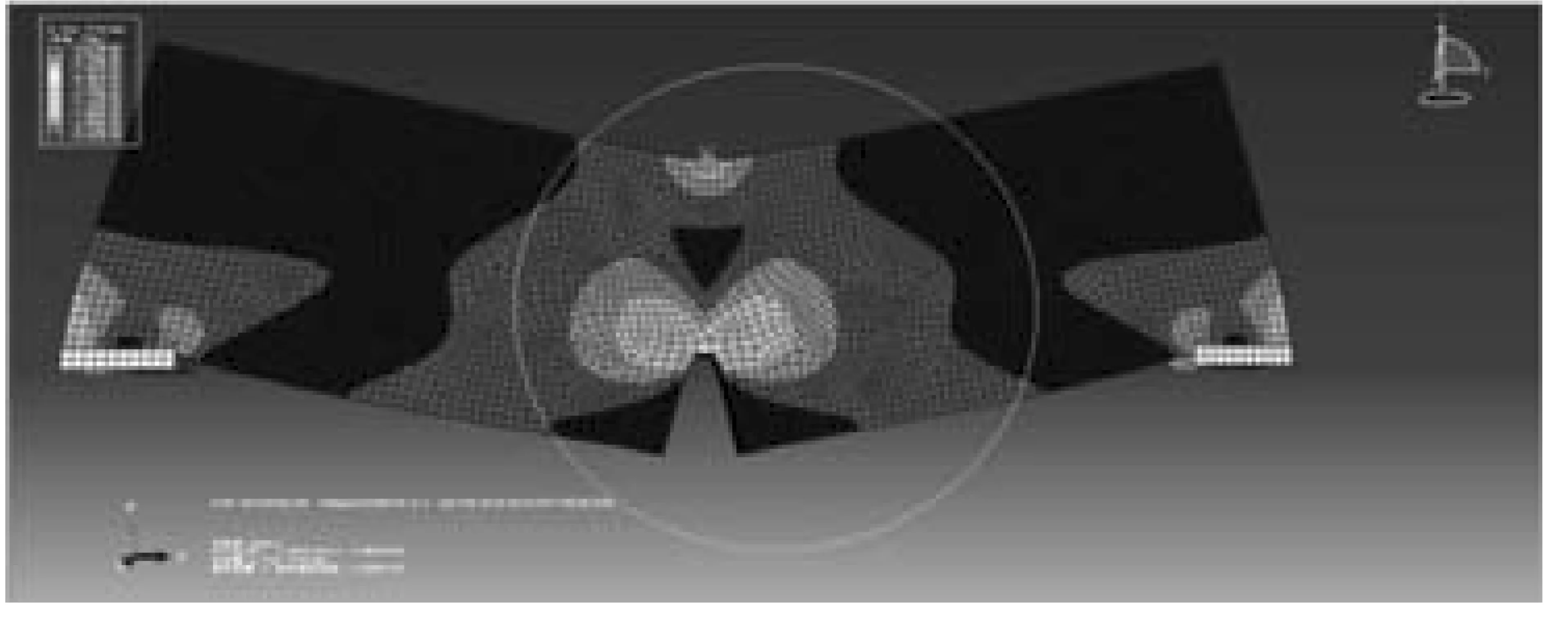
图14 有限元应变云图

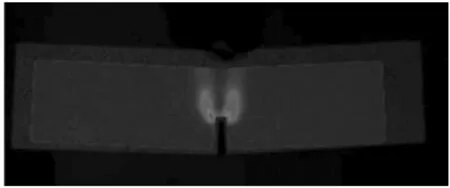
图15 实验应变云图

最后分析裂纹的形成与扩展。由于拍摄的图像只能对正面图像进行分析，而有限元分析中凹槽顶部首先出现裂纹，不能通过分析实验图片来体现，因此直接开始分析正面的裂纹形成与扩展情况。裂纹首先是在两个直角处形成，正中间裂纹也随后开始形成，然后以中间裂纹为主，向上发展，直到铝合金梁完全破坏，如图16所示。这个破坏特点与我们在上个有限元分析模块中得到的分析结论基本类似。

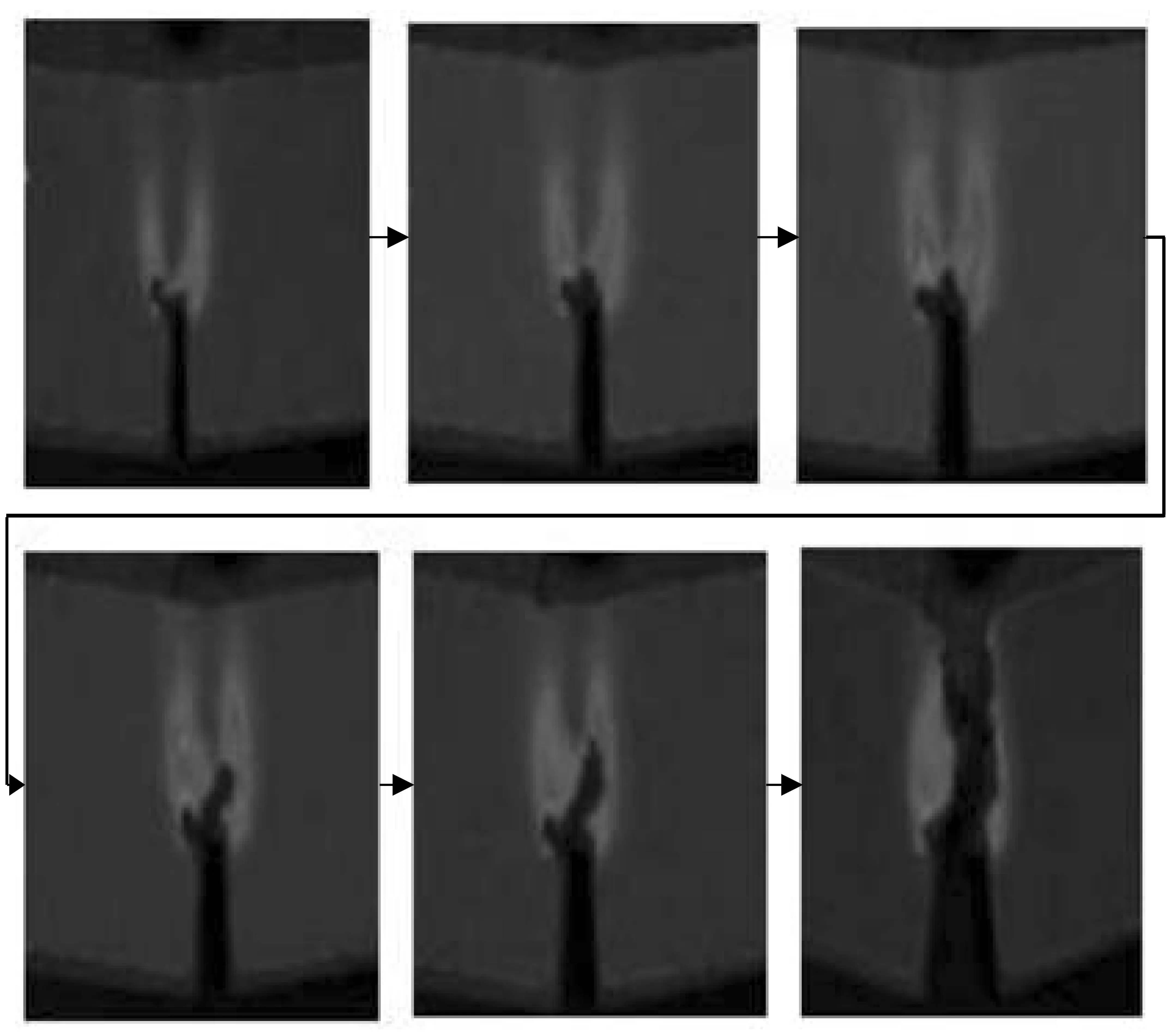
图16 实验裂纹的形成与扩展过程

3.2 误差分析

通过实验所得的最大载荷与有限元模拟有一些误差，应力云图和裂纹扩展的对比也存在一定的误差，对实验过程进行分析，发现可能由以下几点原因导致：

1)实验用的铝合金构件内部可能存在缺陷，在使用前肉眼未能检查出构件内部的缺陷，在裂纹扩展时，内部缺陷会引导裂纹的扩展方向，而有限元分析时，铝合金模拟部件内部不存在任何缺陷，由此会产生一定的误差。

2)实验用万能试验机的支座和夹具部分是强度很大的材料，但不能排除其在加载时会发生微小变形，而有限元模拟时，将这两部分定义为刚体，这也会导致一定程度的误差。

4 结论

1)使用XFEM技术可以在不重新划分网格的情况下，很好地模拟出裂纹的形成和扩展过程，而且模拟结果和实验结果十分吻合，进一步证实了XFEM技术在研究裂纹扩展方面的可行性以及与其他裂纹拓展技术相比的优越性。

2)带裂缝金属梁的裂纹开裂位置通常都在薄弱位置，即裂缝处，而且会在裂纹的两个直角处先发生材料的损坏，因此在对损坏构件进行检测或者修复时要着重注意这些薄弱位置。

3)带裂缝金属梁的裂纹发展过程是首先形成裂纹，在此基础上其周围材料不断发生小范围损伤破坏，并沿着裂纹方向破坏，直至最后整个构件破坏。

该研究成果对于损伤结构的检测、带裂纹材料的修复有借鉴意义，同时给构件剩余寿命预测和安全性评估提供有效信息。

[参考文献]

[1]金建三，李润方.工程断裂力学[J].重庆大学学报(自然科学版)，1978(4)：81-121.

[2]康颖安.断裂力学的发展与研究现状[J].湖南工程学院学报(自科版)，2006，16(1)：39-42.

[3]任大龙，万水，钟志鹏.基于FRANC2D的中央裂纹平板断裂力学分析[J].常州工学院学报，2012,25(3)：1-4.

[4]王慰军.基于ABAQUS的裂纹拓展仿真软件及应用[D].杭州：浙江大学，2006.

[5]刘家菊.5E62铝合金疲劳裂纹扩展行为的有限元模拟[D].北京：北京工业大学，2015.

[6]张新民，邓运来，张勇.高强铝合金的发展及其材料的制备加工技术[J].金属学报，2015，51(3)：257-271.

[7]孟祥琦.铝合金材料的应力腐蚀及腐蚀疲劳特性实验研究[D].上海：上海交通大学，2012.

[8]BELYTSCHKO T，AREIAS P，ZI G.Crack propagation in plates and shells using XFEM[R].The Sixth World Congress on Computational Mechanics in Conjunction with the Second Asian-Pacific Congress on Computational MechanicsⅠ.Beijing，2004.

[9]MELENK J M，BABUSKA I.The partition of unity finite element method：basic theory and applications[J].Computer Methods in Applied Mechanics and Engineering，1996，139(1-4)：289-314.

[10]刁浩峰.基于XFEM的裂纹扩展分析[D].杭州：浙江理工大学,2013.

[11]刘长虹，李洪什，彭军.基于XFEM的裂纹扩展分析[J].上海工程技术大学学报，2010，24(3)：218-220.

[12]石路杨，余天堂.多裂纹扩展的扩展有限元法分析[J].岩土力学，2014(1)：263-272.

[13]董玉文，任青文.基于XFEM的混凝土开裂数值模拟研究[J].重庆交大学学报(自然科学版)，2009，28(1)：36-40.

[14]张红梅.三维六面体网格自适应生成算法研究及其应用[D].济南：山东大学，2007.

[15]胡少伟，鲁文妍.基于XFEM的混凝土三点弯曲梁开裂数值模拟研究[J].华北水利水电大学学报(自然科学版)，2014，35(4)：48-51.