含积分变限函数的求导方法

文传军,陈荣军

(常州工学院数理与化工学院，江苏 常州 213032)

0 引言

含积分变限的函数求导是“高等数学”教学中的一个重要知识点，是考研高数和高数竞赛中的常考内容。在各种《高等数学》或《微积分》教材中，主要针对简单的公式型含积分变限函数求导问题进行讨论，而对于被积函数中也存在求导变量的求导问题，却少有涉及和讨论，常规的处理该类问题的方法较为繁杂，学生学习时掌握起来较为困难，因此值得从事数学基础课教师的关注和研究。

对于含积分变限的函数求导问题的研究文献较少，主要集中在根据具体问题进行分类讨论方面。王凤媛[1]通过研究变限积分的构造，给出解决一类含有变限积分问题的方法。卢亚丽等[2]给出了5个变限积分函数导数定理,并结合实例详细深入地研究了变限积分函数的求导方法。文献[3]针对“高等数学”中变上限积分的求导,从教与学角度给出了该知识点的新的教学和学习的方法,使学生更好地掌握这部分知识,从而增强学生对导数概念的深刻认识。钮宏霞[4]将变限积分求导公式推广到高维空间中变边界的超长方体和超球体上,得到简洁优美的结果,并给出其应用。周少波等[5]针对学生难以掌握的变限定积分的最为一般的求导公式,给出了学生易于理解和接受的一元函数的证明,并用实例展现了这一公式在微积分及其后继课程中的重要应用。姜翠美等[6]结合实例归纳总结不同类型变限积分的求导方法。文献[7]针对变限积分函数求导教学的现状,给出了5个变限积分函数导数定理,并依次对其求导方法进行了深入探究。文献[8]给出了变限积分求导公式的另一种新的证明。吕纪荣等[9]阐述了变限积分函数的定义及其可导性和导数公式，根据导数的定义和定积分的性质,研究了被积函数中含有参变量的变限积分函数的相关性质。

本文对含积分变限的函数求导问题进行了研究，利用复合函数求导法则处理该类问题，分别对积分变限和被积函数中的变量求导，方法简洁有效且形式统一，学生能够快速地掌握并用于处理相关问题。

1 含积分变限函数的求导问题及传统求导方法

1.1 含积分变限函数的求导问题

含积分变限的函数求导问题可归纳为如下三种基本形式：

1)公式型

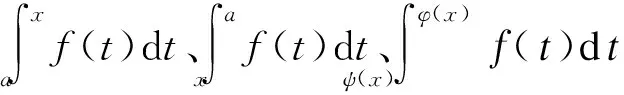
2)乘积型

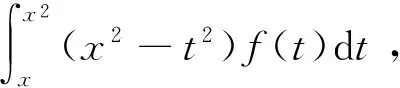
3)换元型

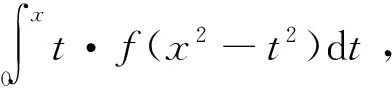
1.2 传统的含积分变限函数的求导方法

1)公式型

对于公式型的变限函数求导，可直接利用公式(1)或者结合定积分相关性质进行计算求解。此类问题已在“高等数学”课程中重点讲解，这里不再详细展开。

(1)

2)乘积型

为了处理乘积型变限函数求导，需要通过拆项分解的方式进行展开化简，即将求导变量x从被积函数中分解出来，使得被积函数中不存在变量x。

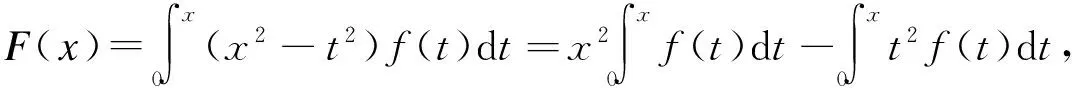
从例1的求解过程来看，传统的求解方法还是比较麻烦的，因为如果将被积函数中的(x2-t2)替换为(x-t)n，则需要一项项展开，而且在(x-t)n的n次方抽象未定的情况下，其实是无法求解的。

3)换元型

为了处理换元型变限函数求导，需要通过换元的方式将变量x从被积函数中分解出来，并且使得被积函数不存在求导变量x。

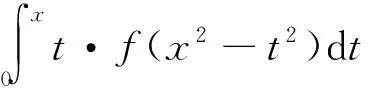
解：设u=x2-t2，当t=0时，u=x2，当t=x时，u=0。且有

所以有

则

从例2的求解可知，处理换元型含积分限的函数求导，需要根据题目的具体情况进行特定的变量代换，没有一种通用的求导方法，这给问题的求解带来麻烦。

另外，对比三种类型的含积分限的函数求导过程，发现这三种类型的问题虽然在本质上是一种问题，但却要分类型单独处理，求导方法不具有通用性，这给学生的学习带来麻烦，如果有一种方法可以通用，就可以减少学习的障碍和提升处理问题的效率。

2 通用的基于复合函数形式的含积分变限函数求导方法

为了能够得到一种通用的含积分限的函数求导方法，将此类问题进行通项分析，并考虑以复合函数的形式进行计算。

2.1 基于复合函数形式的含积分变限函数求导方法

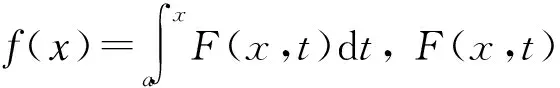
(2)

证明：利用导数定义进行证明

由定积分性质有

由积分中值定理有

其中ξ介于x,x+h之间

当利用定理1进行计算时，积分上限变量x和被积函数中的x被视作复合函数中的两个变量，对x求导意味着分别对这两处的x独立分别求导。当对积分上限x求导时，即可应用积分变限求导法则，直接将积分上限x代入被积函数取代积分变量t，而对被积函数中的x求导时，则相当于被积函数F(x,t)求x的偏导运算。

2.2 对三种类型的含积分变限函数求导运算的形式统一

基于定理1，可以将三种类型的变限积分函数求导运算统一起来。

对于第一种类型公式型，应用定理1可得

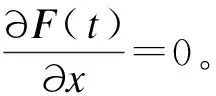
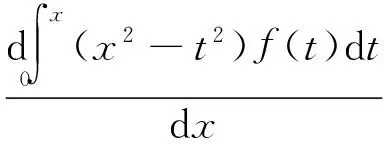
对于第三种类型换元型，以例2为例，即有F(x,t)=t·f(x2-t2)，应用定理1

x·f(0)-x·f(x2-t2)︳x0=x·f(0)-x·f(0)+xf(x2)=xf(x2)

对比1.2和2.2可以发现，使用定理1可以简洁高效地将三种含积分限的函数求导统一起来，该方法简单明了且易于计算。

2.3 定理1在常见含积分变限函数求导问题中的应用

基于定理1处理一些常见的含积分变限的函数求导问题。

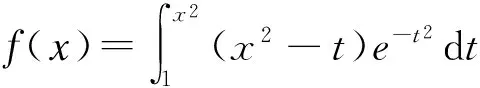
解：根据定理1及复合函数求导法则可得

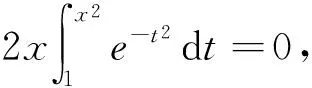
f(x)定义域为，结合从而有解，如表1所示。

总之，无论c是Γ上的哪一种端点，Φ0(z)总以它为常点，因而Φ0(z)在D内全纯.又因Φ1(z)，Χ(z)都连续到L上，且Χ(z)≠0，故Φ0(z)也必连续到L上.

表1 例3的单调区间

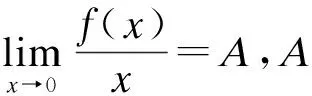
解：

方法1：传统换元法求解

则当x≠0时，

而当x=0时，

u=ht，h[0,1]=[0,h]

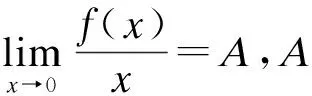
方法2：利用定理1求解

相当于上限x取为常数，则在定理1中对上限的求导为0。

当x≠0时，由定理1可知，

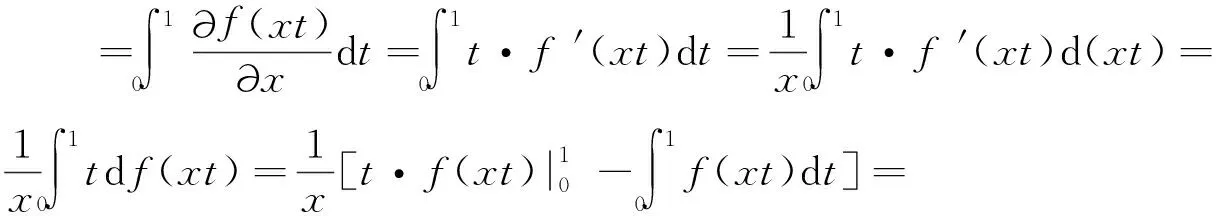
当x=0时类似可得。

3 结论

本文对含积分变限的函数求导进行了研究，利用复合函数求导的方法，将积分变限和被积函数中的求导变量视作复合函数中的两个变量分别求导，实现了多种类型含变限函数的求导方法的统一，便于学生有效学习和掌握，并达到灵活应用的目的。

[参考文献]

[1]王凤媛.导数在解决含有变限积分问题中的应用[J].山西财经大学学报, 2000，22(s1):178-191.

[2]卢亚丽, 李艳华, 李战国,等.变限积分函数求导方法研究[J].河南教育学院学报(自然科学版), 2004,13(1):4-6.

[3]鲁琦.高等数学中变上限积分求导浅析[J].考试周刊, 2008(21):38.

[4]钮宏霞.变限积分求导公式在高维典型立体上的推广[J].数学的实践与认识, 2008, 38(20):234-238.

[5]周少波, 雷冬霞, 程生敏.变限积分的求导公式及其应用[J].学园·教育科研, 2012(19):51-52.

[6]姜翠美, 姜英, 王海霞.变限积分的求导方法[J].高等数学研究, 2013，16(6):23-24.

[7]于风宏.高等数学教学中变限积分函数的求导方法[J].数学学习与研究, 2014(19):75.

[8]郝芳.变限积分求导公式的另一种证明[J].文山学院学报, 2015，28(3):68-69.

[9]吕纪荣, 王士虎.关于变限积分函数求导问题的研究与应用[J].数学学习与研究, 2015(19):134-135.