一种由层次遍历和其它遍历构造二叉树的新算法
王防修,刘春红
(1.武汉轻工大学 数学与计算机学院,湖北 武汉 430023;2.九州通医药集团物流有限公司,湖北 武汉 430040)
一种由层次遍历和其它遍历构造二叉树的新算法
王防修1,刘春红2
(1.武汉轻工大学 数学与计算机学院,湖北 武汉 430023;2.九州通医药集团物流有限公司,湖北 武汉 430040)
在由遍历序列构造二叉树问题的研究中,针对目前还没有用层次遍历和其它遍历一起构造二叉树的问题,提出了一种由层次遍历和其它遍历一起构造二叉树的新算法。考虑到层次遍历中左子树和右子树的层次遍历不具有递归属性,设计了从层次遍历中分离出左右子树层次遍历的方法,并且通过组合得到具有递归属性的层次遍历。通过对层次遍历和中序遍历的递归属性的研究,设计了由层次遍历和中序遍历构造二叉树的递归算法;通过对层次遍历和先序遍历的递归属性的研究,设计了由层次遍历和中序遍历构造没有出度为1的二叉树的递归算法;通过对层次遍历和后序遍历的递归属性的研究,设计了由层次遍历和后序遍历构造没有出度为1的二叉树的递归算法。仿真结果表明,用设计的算法构造二叉树是有效的,可为二叉树的构造提供新算法。
层次遍历;先序遍历;中序遍历;后序遍历;递归算法
1 引言
自然界很多事物本质上是树状结构,如果想用计算机模拟具有树状结构的事物,则必须首先解决树状结构在计算机中的表示问题。由于树和二叉树之间能够相互转化,故只需解决二叉树在计算机内存中的表示即可。因此,用各种算法构造二叉树一直是人们研究的热点问题[2-6]。近年来,通过对二叉树自身特点的研究,出现了很多由遍历序列构造二叉树的递归算法[7,8]和非递归算法[9-12]。虽然这些算法各有不同,但都可以归结为以下三种情形:
(1)由先序遍历序列和中序遍历序列构建二叉树;
(2)由中序遍历序列和后序遍历序列构建二叉树;
(3)由先序遍历序列和后序遍历序列构建二叉树。
然后,除了上述三种情况之外,构造二叉树值得研究的还有下述三种情形:
(1)由层次遍历序列和中序遍历序列构建二叉树;
(2)由层次遍历序列和先序遍历序列构建二叉树。
(3)由层次遍历序列和后序遍历序列构建二叉树。
对于这三种构造二叉树的情形,目前尚未见之于文献。因此,如果能够设计这三种构造二叉树的新算法,则无疑对二叉树的构造具有重要意义。此外,由层次遍历序列和其它遍历序列构建二叉树可能还需要额外的附加条件。针对这些问题, 笔者对这三种构造二叉树的算法进行了理论上的证明,并且分别设计了三种不同的构造二叉树的递归算法。仿真结果表明,这三种新算法都可以用来构造二叉树。
2 由层次遍历和其它遍历构造二叉树的数学原理
定理1 如果已知一棵二叉树的层次遍历序列和中序遍历序列,则可用递归算法建立该二叉树。
证明设W=wiwi+1…wj和Y=ykyk+1…yl分别表示二叉树T的层次遍历序列和中序遍历序列,则由层次遍历序列的性质可知二叉树T的根结点是wi。由二叉树的性质可知,在中序遍历序列存在唯一的元素ym,使得ym=wi。因此,中序遍历序列Y可以进行如下划分:
Y=(yk…ym-1)ym(ym+1…yl)
(1)
根据二叉树中序遍历序列的性质可知,Y1=yk…ym-1是T的左子树的中序遍历,而Y2=ym+1…yl是T的右子树的中序遍历。
如果对层次遍历序列W进行如下划分:
W1={wq|wq∈Y1,q=i+1,…,j}
(2)
W2={wq|wq∈Y2,q=i+1,…,j}
(3)
则由二叉树的层次遍历的性质可知,W1是二叉树T的左子树的层次遍历,而W2是二叉树T的右子树的层次遍历。
如果对层次遍历序列W进行如下重组:
W=wiW1W2
(4)
则存在p∈{i+1,…,j},使得W进行如下划分:
W=wi(wi+1…wp)(wp+1…wj)
(5)
其中W1=wi+1…wp是T的左子树的层次遍历,而W2=wp+1…wjT的右子树的层次遍历。
由Y1与W1的长度相等 ,有
p=m+i-k
(6)
由Y2与W2的长度相等 ,有
p=m+j-l
(7)
由于W和Y的长度相等,故有j-i=l-k,从而式(6)和式(7)表示的p值相等。
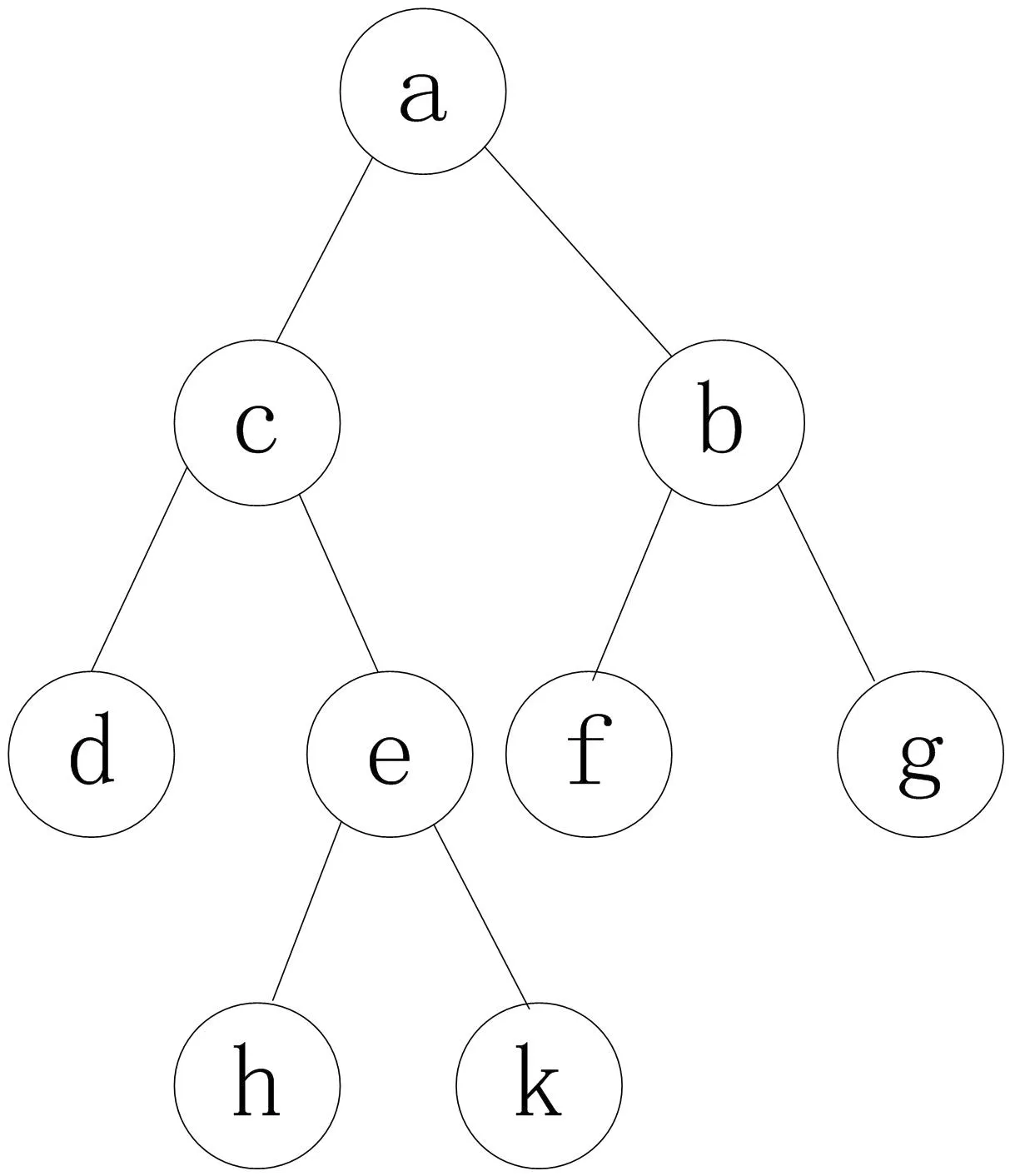
递归子结构:如果m>k,则二叉树T的左孩子由左子树的层次遍历W1=wi+1…wp和中序遍历Y1=yk…ym-1确定;如果m 递归终止条件:如果m=k,则二叉树T无左孩子;如果m=l,则二叉树T无右孩子。 定理2 如果已知一棵二叉树的层次遍历序列和先序遍历序列,并且该二叉树没有出度为1的结点,则可用递归算法建立该二叉树。 证明 如果二叉树存在出度为1的结点,则由层次遍历序列和先序遍历序列所对应的二叉树不唯一,故无法构造该二叉树。如果不存在出度为1的结点,则设W=wiwi+1…wj和X=xkxk+1…xl分别是二叉树T的层次遍历和先序遍历。由二叉树层次遍历和先序遍历的性质可知wi和xk都是二叉树T的根结点,故wi=xk。由二叉树的性质可知,在先序遍历序列存在唯一的元素xm,使得xm=wi+2。因此,先序遍历序列X可以进行如下划分: X=xk(xk+1…xm-1)(xm…xl) (8) 根据二叉树先序遍历序列的性质可知,X1=xk+1…xm-1是T的左子树的先序遍历,而X2=xm…xl是T的右子树的先序遍历。 如果对层次遍历序列W进行如下划分: W1={wq|wq∈X1,q=i+1,…,j} (9) W2={wq|wq∈X2,q=i+1,…,j} (10) 则由二叉树的层次遍历的性质可知,W1是二叉树T的左子树的层次遍历,而W2是二叉树T的右子树的层次遍历。 如果令W=wiW1W2,则∃p∈{i+1,…,j},使得W1=wi+1…wp和W2=wp+1…wj。 由X1与W1的长度相等 ,有 p=m+i-k-1 (11) 由X2与W2的长度相等 ,有 p=m+j-l-1 (12) 由j-i=l-k可知式(11)和式(12)的值相等。 递归子结构:如果m>k,则二叉树T的左孩子由左子树的层次遍历W1=wi+1…wp和先序遍历X1=xk+1…xm-1确定;如果m 递归终止条件:如果l=k,则二叉树T既无左孩子又无右孩子。 定理3 如果已知一棵二叉树的层次遍历序列和后序遍历序列,并且该二叉树没有出度为1的结点,则可用递归算法建立该二叉树。 证明如果二叉树存在出度为1的结点,则由层次遍历序列和后序遍历序列所对应的二叉树不唯一,故无法构造该二叉树。如果不存在出度为1的结点,则设W=wiwi+1…wj和Z=zkzk+1…zl分别是二叉树T的层次遍历和后序遍历。由二叉树层次遍历和后序遍历的性质可知wi和zl都是二叉树T的根结点,故wi=zl。由二叉树的性质可知,在后序遍历序列存在唯一的元素zm,使得zm=wi+1。因此,后序遍历序列Z可以进行如下划分: Z=(zk…zm)(zm+1…zl-1)zl (13) 根据二叉树后序遍历序列的性质可知,Z1=zk…zm是T的左子树的后序遍历,而Z2=zm+1…zl-1是T的右子树的后序遍历。 如果对层次遍历序列W进行如下划分: W1={wq|wq∈Z1,q=i+1,…,j} (14) W2={wq|wq∈Z2,q=i+1,…,j} (15) 则由二叉树的层次遍历的性质可知,W1是二叉树T的左子树的层次遍历,而W2是二叉树T的右子树的层次遍历。 如果令W=wiW1W2,则∃p∈{i+1,…,j},使得W1=wi+1…wp和W2=wp+1…wj。 由Z1与W1的长度相等 ,有 p=m+i-k+1 (16) 由Z2与W2的长度相等 ,有 p=m+j-l+1 (17) 由j-i=l-k可知式(16)和式(17)的值相等。 递归子结构:如果m>k,则二叉树T的左孩子由左子树的层次遍历W1=wi+1…wp和后序遍历Z1=zk…zm确定;如果m 递归终止条件:如果l=k,则二叉树T既无左孩子又无右孩子。 3.1 由层次遍历序列和中序遍历序列构造二叉树 为方便算法设计,不妨设建立二叉树的递归函数为T=f(W,Y,i,j,k,l),则其递归过程可以描述如下: (1)由层次遍历序列W=wiwi+1…wj可知W中的第一个元素wi是二叉树T的根结点。 (2)从中序遍历序列Y中查找元素ym,使得ym=wi。根据式(1)得到左子树的中序遍历Y1和右子树的中序遍历Y2。 (3)根据式(2)从层次遍历W中分离出左子树的层次遍历W1,根据式(3)从层次遍历W中分离出右子树的层次遍历W2。 (4)根据式(5)重新组装W=wiW1W2。 (5)如果m=k,则根结点T没有左孩子;否则,二叉树的根结点T的左孩子是其左子树的根结点,若设其左孩子为Tl,则式(6)或式(7)分别有 Tl=f(W,Y,i+1,m+i-k,k,m-1) (18) 或 Tl=f(W,Y,i+1,m+j-l,k,m-1) (19) (6)如果m=l,则二叉树的根结点T没有右孩子;否则,根结点T的右孩子是其右子树的根结点。若设T的右孩子为Tr,则有 Tr=f(X,Y,m+i-k+1,j,m+1,l) (20) 或 Tr=f(X,Y,m+j-l+1,j,m+1,l) (21) (7)当递归过程结束时,则得到一个根结点为T的二叉树。 3.2 由层次遍历序列和先序遍历序列构造无出度为1的二叉树 为方便算法描述,设建立二叉树的递归函数为T=g(W,X,i,j,k,l),其递归过程描述如下: (1)先序遍历序列X=xkxk+1…xl中的元素xk是二叉树T的根结点; (2)从先序遍历序列X中查找元素xm,使得xm=wi+2。根据式(8)得到左子树的先序遍历X1和右子树的先序遍历X2 (3)根据式(9)从层次遍历W中分离出左子树的层次遍历W1,根据式(10)从层次遍历W中分离出右子树的层次遍历W2。 (4)由W=wiW1W2重新组装层次遍历。 (5)如果m>k,则二叉树的根结点T的左孩子是其左子树的根结点,若设其左孩子为Tl,则式(11)或式(12)分别有 Tl=g(W,X,i+1,m+i-k-1,k+1,m-1) (22) 或 Tl=g(W,X,i+1,m+j-l-1,k+1,m-1) (23) (6)如果m Tr=g(W,X,m+i-k,j,m,l) (24) 或 Tr=g(W,X,m+j-l,j,m,l) (25) (7)如果l=k,则二叉树T既没有左孩子又没有右孩子。 (8)当递归过程结束时,则得到一个根结点为T的二叉树。 3.3 由层次遍历序列和后序遍历序列建立无出度为1的二叉树 为方便算法描述,设建立二叉树的递归函数为T=h(W,Z,i,j,k,l),则其递归过程描述如下: (1)后序遍历序列Z=zkzk+1…zl中的元素zl是二叉树T的根结点。 (2)从后序遍历序列Z中查找元素zm,使得zm=wi+1。根据式(13)得到左子树的后序遍历Z1和右子树的后序遍历Z2。 (3)根据式(14)从层次遍历W中分离出左子树的层次遍历W1,根据式(15)从层次遍历W中分离出右子树的层次遍历W2。 (4)由W=wiW1W2重新组装层次遍历。 (5)如果m>k,则二叉树的根结点T的左孩子是其左子树的根结点,若设其左孩子为Tl,则式(16)或式(17)分别有 Tl=h(W,Z,i+1,m+i-k+1,k,m) (26) 或 Tl=h(W,Z,i+1,m+j-l+1,k,m) (27) (6)如果m Tr=h(W,Z,m+i-k+2,j,m+1,l-1) (28) 或 Tr=h(W,Z,m+j-l+2,j,m+1,l-1) (29) (7)如果l=k,则二叉树T既没有左孩子又没有右孩子。 (8)当递归过程结束时,则得到一个根结点为T的二叉树。 算例 用上述三种算法构造如图1所示的二叉树。 图1 二叉树 解 由图1可以得到如表1所示的遍历序列。 表1 二叉树的遍历序列 i123456789wiacbdefghKyidchekafbGxiacdehkbfgzidhkecfgba 表1中,W=w1w2…w9表示二叉树的层次遍历序列,Y=y1y2…y9表示二叉树的中序遍历序列,X=x1x2…x9表示二叉树的先序遍历序列,而Z=z1z2…z9表示二叉树的后序遍历序列。 方法一 根据算法3.1,由层次遍历序列W和中序遍历序列Y构造二叉树的过程如下: (4)当m=8时,由f(W,Y,8,8,7,7)得w7(b)的左孩子为w8(f)和m=7,而由m=7可知w8(f)是叶子结点;由f(W,Y,9,9,9,9)得w7(b)的右孩子为w9(g)和m=9,而由m=9可知w9(g)是叶子结点。 (5)当m=4时,由f(W,Y,5,5,3,3)得w4(e)的左孩子为w5(h)和m=3,而由m=3可知w5(h)是叶子结点;由f(W,Y,6,6,5,5)得w4(e)的右孩子为w6(k)和m=5,而由m=5可知w6(k)是叶子结点。 方法二 根据算法3.2,由层次遍历序列W和先序遍历序列X构造二叉树的过程如下: (4)当m=9时,由g(W,X,8,8,8,8)得x7(b)的左孩子为x8(f)和l=k=8,而由l=k可知x8(f)是叶子结点;由g(W,X,9,9,9,9)得x7(b)的右孩子为x9(g)和l=k=9,而由l=k可知x9(g)是叶子结点。 (5)当m=6时,由f(W,X,5,5,5,5)得x4(e)的左孩子为x5(h)和l=k=5,而由l=k可知x5(h)是叶子结点;由f(W,X,6,6,6,6)得x4(e)的右孩子为x6(k)和l=k=6,而由l=k可知x6(k)是叶子结点。 方法三 根据算法3.3,由层次遍历序列W和后序遍历序列Z构造二叉树的过程如下: (4)当m=6时,由f(W,X,8,8,6,6)得z8(b)的左孩子为z6(f)和l=k=6,而由l=k可知z6(f)是叶子结点;由f(W,X,9,9,7,7)得z8(b)的右孩子为z7(g)和l=k=7,而由l=k可知z7(g)是叶子结点。 (5)当m=2时,由g(W,Z,5,5,2,2)得z4(e)的左孩子为z2(h)和l=k=2,而由l=k可知z2(h)是叶子结点;由h(W,Z,6,6,3,3)得z4(e)的右孩子为z3(k)和l=k=3,而由l=k可知z3(k)是叶子结点。 本文设计了由层次遍历和其它遍历构造二叉树的三种递归算法。算法仿真表明,由层次遍历和中序遍历可以递归建立二叉树,由层次遍历和先序遍历可以递归建立无出度为1的二叉树,由层次遍历和后序遍历也可以递归建立无出度为1的二叉树。同以前所有构造二叉树的传统算法一样,本文设计的算法要求遍历序列中不能有相同元素出现。因此,由具有相同元素的遍历序列构造二叉树的算法是未来研究的重点。此外,虽然递归算法结构清晰,方便算法设计,但递归算法运行效率较低,其耗费的计算时间和占用的存储空间都比非递归算法要多,故本文所提问题的非递归算法也是接下来的研究方向。 [1] 严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,1992. [2] Xiang L M,Lawi A,Ushijima K.On constructing a binary tree from its traversals[J].Research Reports on Information Science and Electrical Engineering of Kyushu University,2000, 5(1):13-18. [3] Mikinen E.Constructing a binary tree efficiently from its traversals[J]. International Journal of Computer Mathematics, 2000,75(2):143-147. [4] 唐自立.基于遍历序列的构造树的算法[J].苏州大学学报(自然科学版),2011,27(3):26-29. [5] 唐自立.由先序序列和结点的左孩子情况构造严格二叉树的高效算法[J].南通大学学报(自然科学版),2013,12(1):9-13. [6] 唐自立.由后序序列和结点的双亲情况构造严格二叉树的非递归算法[J].南通职业大学学报,2014,28(4):93-98. [7] 刘璐.由遍历序列构造二叉树的非递算法实现[J].衡水学院学报,2009,11(4):37-40. [8] 王防修,周 康.基于二叉排序树的二叉树建立[J].武汉工业学院学报,2013,32(3):53-57. [9] 李丽姝.利用遍历序列还原二叉树算法的研究与实现[J].电大理工, 2010,242(1) :53-54. [10] 赵刚,李昆.由遍历序列确定二叉树.[J]南昌航空大学学报,2010,24(1):55-59. [11] 朱涛.基于遍历序列重构二叉结构树的分析[J].红河学院学报,2013,11(2):27-30. [12] 化志章.基于遍历序列恢复二叉树的新解法及其证明[J].江西师范大学学报,2013,37(3):268-272. A new algorithm which constructs the binary tree by using the level traversal and the other traversal WANG Fang-xiu1,LIU Chun-hong2 (1. School of Mathematics and Computer Science,Wuhan Polytechnic University, Wuhan 430023,China;2.Jointown Pharmaceutical Group Logistics Co., Ltd. Wuhan 430040,China) In the study which uses traversal sequences to construct the binary tree, in view of The fact that it is not used to construct the binary tree by using the level traversal and the other traversal, a new algorithm is put forward to construct the binary tree by using the level traversal and the other traversal. Considering that there is not recursive attribute in the level traversal of the left sub tree and the right sub tree, a method is designed to isolate the left subtree level traversal and the right subtree level traversal from the level traversal, and recursive property is gained through the combination with the two sub level traversals. By the recursive property of the level traversal and the inorder traversal, a recursive algorithm is designed to construct the binary tree by using the level traversal and inorder traversal. Through the research of the recursive attribute between the level traversal and the preorder traversal,a recursive algorithm is designed to construct the binary tree. By the research of the recursive attribute between the level traversal and the postorder traversal, a recursive algorithm is designed to construct the binary tree. The simulation results show that the algorithm is effective for constructing the binary tree and can provide a new algorithm for the construction of the binary tree. Level traversal; preorder traversal; inorder traversal; postorder traversal; recursive algorithm 2016-05-26 王防修(1973-),男,副教授,E-mail:wfx323@126.com 国家自然科学基金资助项目(61179032)。 2095-7386(2016)04-0067-06 10.3969/j.issn.2095-7386.2016.04.013 TP391 A3 由层次遍历和其它遍历建立二叉树的算法设计
4 算法仿真

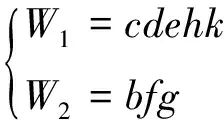


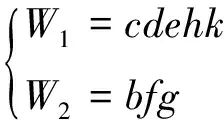


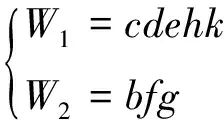


5 结束语
——基于二叉树的图像加密

